ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 125
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, (1.12.1)
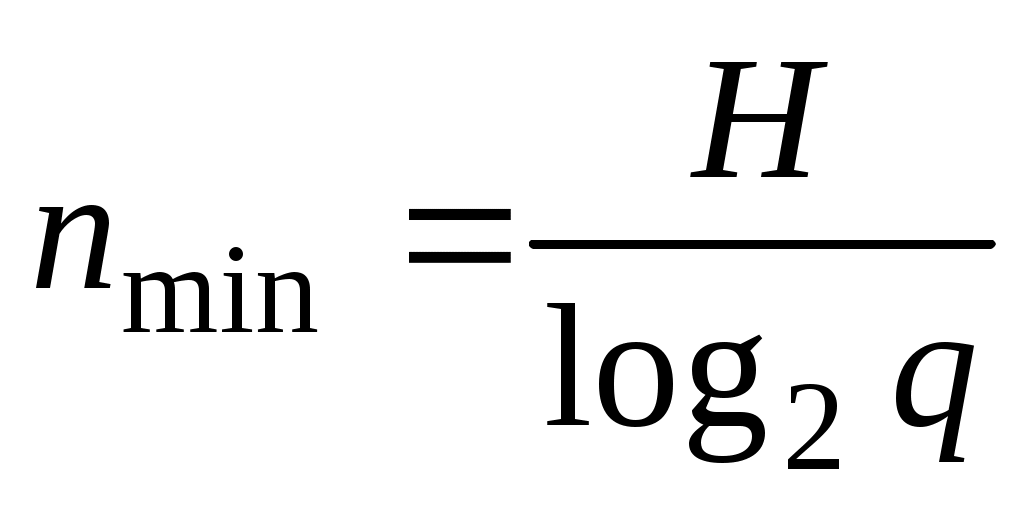 . В нашем случае
. В нашем случае  , т. е. код практически не имеет избыточности. Видно, что среднее число двоичных символов стремится к энтропии сообщения.
, т. е. код практически не имеет избыточности. Видно, что среднее число двоичных символов стремится к энтропии сообщения.
Вторая теорема Шеннона устанавливает принципы помехоустойчивого кодирования. Оказывается, что даже при наличии помех в канале связи всегда можно найти такую систему кодирования, при которой сообщение будет передано с заданной достоверностью. Основная идея всех таких кодов заключается в следующем: для исправления возможных ошибок вместе с основным сообщением нужно передавать какую-то дополнительную информацию. Для реализации контроля возможных ошибок используются так называемые самокорректирующие коды, а по каналу связи вместе с символами основного сообщения передаются ещё
символами основного сообщения передаются ещё 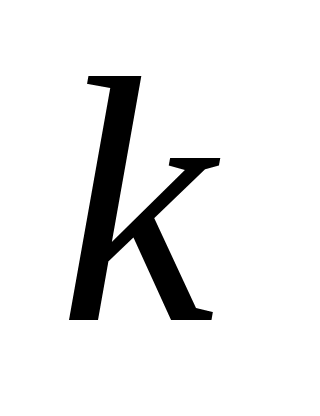 дополнительных символов, обеспечивающих избыточность кодирования и позволяющих противодействовать помехам.
дополнительных символов, обеспечивающих избыточность кодирования и позволяющих противодействовать помехам.
Учение о высказываниях — алгебра высказываний или алгебра логики является простейшей логической теорией. Она рассматривает конечные конфигурации символов и взаимоотношения между ними.
Высказывание — это всякое повествовательное предложение, утверждающее что-либо о чем-либо, при этом непременно истинное или ложное. Логическими значениями высказываний являются "истина" и "ложь", обозначаемые 1 и 0. Высказывания, представляющие собой одно утверждение, называются простыми или элементарными, высказывания, получающиеся из элементарных с помощью грамматических связок "не", "и", "или", "если… , то…", называются сложными. Эти названия не носят абсолютного характера, высказывания, которые в одной ситуации можно считать простыми, в другой ситуации будут сложными. В алгебре логики все высказывания рассматриваются только с точки зрения их логического значения, житейское содержание игнорируется. Каждое высказывание может быть либо истинным, либо ложным, ни одно высказывание не может быть одновременно истинным и ложным. Элементарные высказывания обозначаются строчными буквами латинского алфавита: а, b, с. Из высказываний с помощью логических связок образуются новые высказывания. Рассмотрим наиболее употребительные логические связки.
Отрицанием высказывания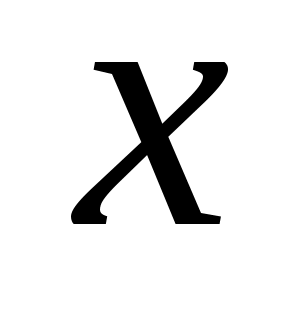 называется новое высказывание, которое является истинным, если высказывание
называется новое высказывание, которое является истинным, если высказывание 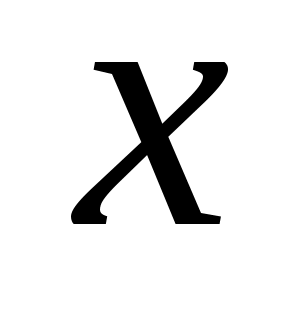 ложно, и ложным, если
ложно, и ложным, если 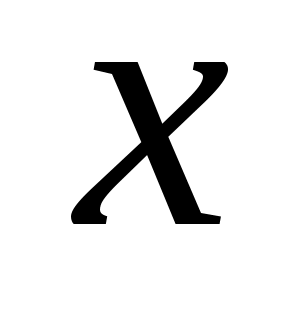 — истинно. Обозначается
— истинно. Обозначается 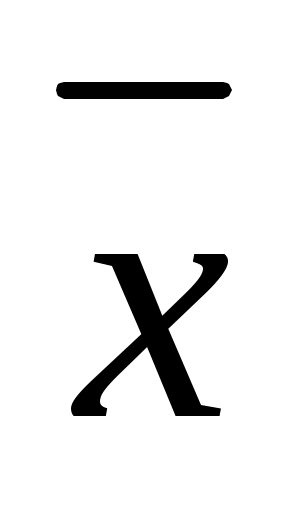 , читается "не
, читается "не 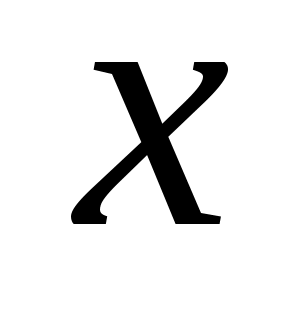 " или "неверно, что
" или "неверно, что 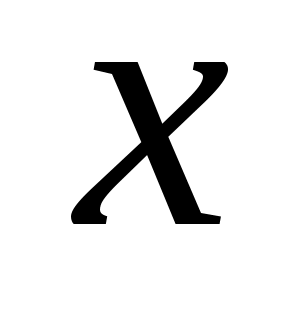 ". Все логические значения высказывания
". Все логические значения высказывания 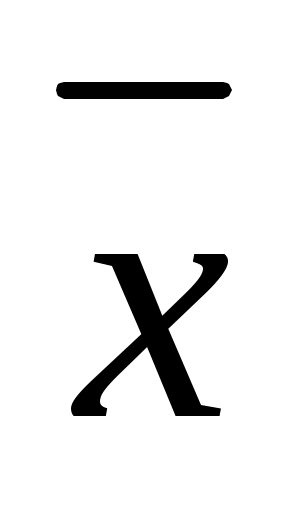
можно описать с помощью табл. 1.13. Если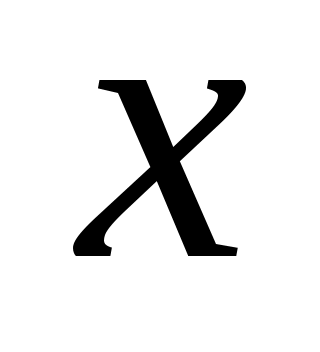 — высказывание, то
— высказывание, то  — противоположное высказывание. Тогда можно образовать
— противоположное высказывание. Тогда можно образовать  , которое называется двойным отрицанием высказывания. Логические значения
, которое называется двойным отрицанием высказывания. Логические значения  , очевидно, совпадают со значениями
, очевидно, совпадают со значениями  . Эта операция одноместная — в том смысле, что из одного данного простого высказывания
. Эта операция одноместная — в том смысле, что из одного данного простого высказывания  строится новое высказывание
строится новое высказывание  .
.
Логическое умножение (конъюнкция). Конъюнкцией двух высказываний и
и 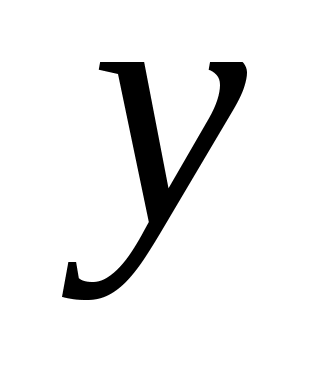 называется новое высказывание
называется новое высказывание  , которое истинно только когда оба высказывания
, которое истинно только когда оба высказывания  и
и 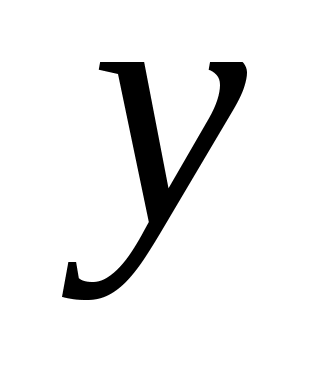 истинны, и ложно, когда хотя бы одно из
истинны, и ложно, когда хотя бы одно из  и
и 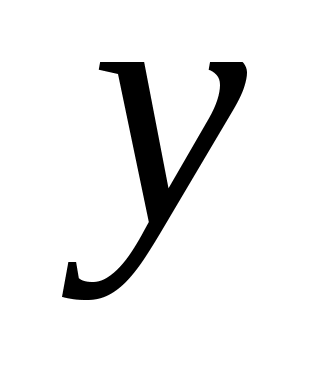 ложно. Обозначается
ложно. Обозначается 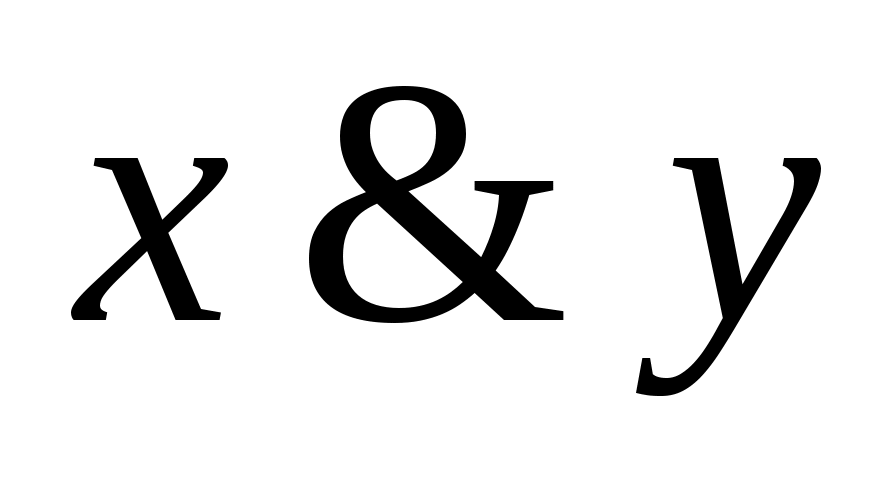 или
или  , читается "
, читается " и
и 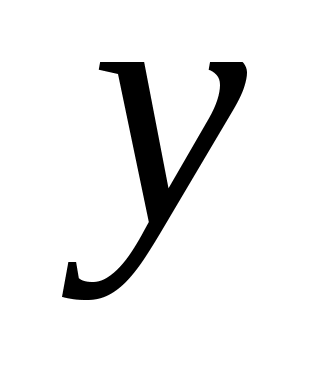 ". Таблица истинности конъюнкции дана в табл. 1.14. Из определения операции конъюнкции видно, что союз "и" в алгебре логики употребляется в том же смысле, что и в повседневной речи. Однако в алгебре логики этой связкой можно связывать любые, сколь угодно далекие по смыслу высказывания. Конъюнкцию часто называют логическим умножением.
". Таблица истинности конъюнкции дана в табл. 1.14. Из определения операции конъюнкции видно, что союз "и" в алгебре логики употребляется в том же смысле, что и в повседневной речи. Однако в алгебре логики этой связкой можно связывать любые, сколь угодно далекие по смыслу высказывания. Конъюнкцию часто называют логическим умножением.
Таблица 1.13 Таблица 1.14
Логическое сложение (дизъюнкция). Дизъюнкцией двух высказываний и
и  называется новое высказывание, которое считается истинным, если хотя бы одно из высказываний
называется новое высказывание, которое считается истинным, если хотя бы одно из высказываний  и
и  истинно, и ложным, если они оба ложны. Обозначается
истинно, и ложным, если они оба ложны. Обозначается  , читается "
, читается " или
или  ". Логические значения дизъюнкции описываются в табл.1.15.
". Логические значения дизъюнкции описываются в табл.1.15.
Таблица 1.15 Таблица 1.16
Импликация или логическое следование. Импликацией двух высказываний и
и  называется новое высказывание, которое считается ложным, когда
называется новое высказывание, которое считается ложным, когда  истинно, а y ложно, и истинным во всех остальных случаях. Обозначается
истинно, а y ложно, и истинным во всех остальных случаях. Обозначается  , читается "если
, читается "если  , то
, то  " или "из
" или "из  следует
следует  ". Высказывание
". Высказывание  называется условием или посылкой, высказывание
называется условием или посылкой, высказывание 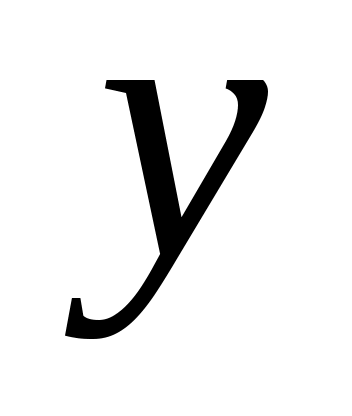 — следствием или заключением. Таблица истинности этой операции приведена в табл. 1.16. Из таблицы истинности видно, что если условие
— следствием или заключением. Таблица истинности этой операции приведена в табл. 1.16. Из таблицы истинности видно, что если условие  — истинно, и истинна импликация
— истинно, и истинна импликация 
Вторая теорема Шеннона устанавливает принципы помехоустойчивого кодирования. Оказывается, что даже при наличии помех в канале связи всегда можно найти такую систему кодирования, при которой сообщение будет передано с заданной достоверностью. Основная идея всех таких кодов заключается в следующем: для исправления возможных ошибок вместе с основным сообщением нужно передавать какую-то дополнительную информацию. Для реализации контроля возможных ошибок используются так называемые самокорректирующие коды, а по каналу связи вместе с
1.13. Математические основы информатики
1.13.1. Алгебра высказываний (алгебра логики)
Учение о высказываниях — алгебра высказываний или алгебра логики является простейшей логической теорией. Она рассматривает конечные конфигурации символов и взаимоотношения между ними.
Высказывание — это всякое повествовательное предложение, утверждающее что-либо о чем-либо, при этом непременно истинное или ложное. Логическими значениями высказываний являются "истина" и "ложь", обозначаемые 1 и 0. Высказывания, представляющие собой одно утверждение, называются простыми или элементарными, высказывания, получающиеся из элементарных с помощью грамматических связок "не", "и", "или", "если… , то…", называются сложными. Эти названия не носят абсолютного характера, высказывания, которые в одной ситуации можно считать простыми, в другой ситуации будут сложными. В алгебре логики все высказывания рассматриваются только с точки зрения их логического значения, житейское содержание игнорируется. Каждое высказывание может быть либо истинным, либо ложным, ни одно высказывание не может быть одновременно истинным и ложным. Элементарные высказывания обозначаются строчными буквами латинского алфавита: а, b, с. Из высказываний с помощью логических связок образуются новые высказывания. Рассмотрим наиболее употребительные логические связки.
Отрицанием высказывания
можно описать с помощью табл. 1.13. Если
Логическое умножение (конъюнкция). Конъюнкцией двух высказываний
Таблица 1.13 Таблица 1.14
| | | |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
-


1
0
0
1
Логическое сложение (дизъюнкция). Дизъюнкцией двух высказываний
Таблица 1.15 Таблица 1.16
| | | |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| | | |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
Импликация или логическое следование. Импликацией двух высказываний