Файл: Чувашский государственный педагогический университет им. И. Я. Яковлева.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 109
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
называется фигура, состоящая из точек и соединяющих их отрезков .
Точки называют вершинами многоугольника, а отрезки – его сторонами. Две вершины назыаются смежными, если они соединяются стороной многоугольника.
Диагональю многоугольника называют отрезок, соединяющий две несмежные вершины.
Многоугольник называется выпуклым, если он расположен в одной полуплоскости относительно прямой, содержащей любую сторону.
Сумма внутренних углов произвольного выпуклого многоугольника находят по формуле, где – число сторон (углов) многоугольника.
Периметром многоугольника называют сумму длин всех его сторон.
Многоугольник называется правильным, все его стороны равны и все его углы равны.
1.3. Треугольники
Сумма углов любого треугольника равна.
Любая сторона треугольника меньше суммы длин двух других его сторон.
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Свойства медиан.
точкой в отношении 2:1, считая от вершины треугольника.
Биссектрисой треугольника называется прямая, делящая его внутренний угол пополам.
Свойства биссектрис.
Высотой называется перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противоположную сторону треугольника.
В подобных треугольниках пропорциональны все их линейные элементы (с одним и тем же – коэффициентом подобия): стороны, медианы, биссектрисы, векторы, радиусы вписанных и описанных окружностей и пр.
Отношение площадей подобных треугольников равно.
1.4. Четырехугольники
Четырехугольник, у которого противоположные стороны попарно параллельны, называются параллелограммом.
Свойства параллелограмма.
Параллелограмм, у которого все стороны равны, называется ромбом. Диагонали ромбы взаимно перпендикулярны и являются биссектрисами его внутренних углов.
Параллелограмм, у которого все углы прямые, называется прямоугольником.
Теоремы.
Четырехугольник, две стороны которого параллельны, а две - нет, называется трапецией.
Теоремы.
1.5. Окружность и круг
Окружность – множество всех точек плоскости, равноудаленных от одной точки.
Хорда – отрезок, соединяющий две точки окружности.
Равные хорды окружности равноудалены от ее центра; равноудаленные от центра окружности хорды равны.
Диаметр – хорда, проходящая через центр.
Касательная – прямая, имеющая с окружностью одну общую точку.
Центральный угол – угол с вершиной в центре окружности.
Вписанный угол – угол с вершиной на окружности, стороны которого пересекают окружность.
Теоремы, относящиеся к окружности.
1.6. Основные формулы планиметрии
1. Произвольный треугольник (– стороны; –противолежащие им углы; - полупериметр; – радиус описанной окружности; – радиус вписанной окружности; – площадь; - высота, проведенная к стороне)
(теорема косинусов); (теорема синусов);.
2. Прямоугольный треугольник (– катеты; – гипотенуза; – проекции на гипотенузу)
;.
3. Равносторонний треугольник;; .
4. Произвольный выпуклый четырехугольник (и –диагонали, – угол между ними, – площадь)
5. Параллелограмм (и – смежные стороны, – угол между ними, – высота, проведенная к стороне ) ;; .
6. Ромб.
7. Прямоугольник .
8. Квадрат ( – диагональ) .
9. Трапеция (и – основания, – расстояние между ними, – средняя линия) ;.
10. Описанный многоугольник (– полупериметр, – радиус вписанной окружности) .
11. Правильный многоугольник (– сторона правильного – угольника, – радиус описанной окружности, – радиус вписанной окружности) .
12. Окружность, круг (– радиус, – длина окружности,– площадь круга) ;.
13. Сектор (– длина дуги, ограничивающей сектор, – градусная мера центрального угла, – радиальная мера центрального угла) ; .
§2. Решение задач и задач ЕГЭ с применением математического пакета Geogebra
2.1. Произвольный треугольник
Задача 1. Медианы треугольника ABC разрезают его на 6 треугольников. Докажите, что центры описанных окружностей этих треугольников лежат на одной окружности.
Создание чертежа. Пусть – медианы, – точка их пресечения
Шаги создания чертежа в GeoGebra (таб. 1):
Таблица 1
Из чертежа (рис. 15) видно, центры описанных окружностей треугольниковлежат на одной окружности. Далее можно проводить доказательство.
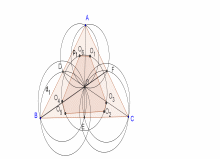
Рис. 15
Точки называют вершинами многоугольника, а отрезки – его сторонами. Две вершины назыаются смежными, если они соединяются стороной многоугольника.
Диагональю многоугольника называют отрезок, соединяющий две несмежные вершины.
Многоугольник называется выпуклым, если он расположен в одной полуплоскости относительно прямой, содержащей любую сторону.
Сумма внутренних углов произвольного выпуклого многоугольника находят по формуле, где – число сторон (углов) многоугольника.
Периметром многоугольника называют сумму длин всех его сторон.
Многоугольник называется правильным, все его стороны равны и все его углы равны.
1.3. Треугольники
Сумма углов любого треугольника равна.
Любая сторона треугольника меньше суммы длин двух других его сторон.
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Свойства медиан.
-
Медианы треугольника пересекаются в одной точке и делятся этой
точкой в отношении 2:1, считая от вершины треугольника.
-
Медиана делит треугольник на два равновеликих (имеющих одинаковые площади) треугольника. -
Три медианы делят треугольник на шесть равновеликих треугольника. Отрезки, соединяющие точку пересечения медиан с вершинами, делят треугольник на три равновеликих треугольника.
Биссектрисой треугольника называется прямая, делящая его внутренний угол пополам.
Свойства биссектрис.
-
Биссектриса треугольника делит его сторону на части, пропорциональные прилежащим сторонам. -
Центр окружности, вписанной в угол, лежит на биссектрисе этого угла. Радиус окружности перпендикулярен стороне угла в точке касания. -
Центр окружности, вписанной в треугольник, находится в точке пересечения биссектрис углов треугольника. -
Центр окружности, описанной около треугольника, расположен в точке пересечения серединных перпендикуляров к сторонам.
Высотой называется перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противоположную сторону треугольника.
В подобных треугольниках пропорциональны все их линейные элементы (с одним и тем же – коэффициентом подобия): стороны, медианы, биссектрисы, векторы, радиусы вписанных и описанных окружностей и пр.
Отношение площадей подобных треугольников равно.
1.4. Четырехугольники
Четырехугольник, у которого противоположные стороны попарно параллельны, называются параллелограммом.
Свойства параллелограмма.
-
Противоположные стороны параллелограмма равны. -
Противоположные углы параллелограмма равны. -
Диагонали параллелограмма делятся точкой пересечения пополам. -
Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.
Параллелограмм, у которого все стороны равны, называется ромбом. Диагонали ромбы взаимно перпендикулярны и являются биссектрисами его внутренних углов.
Параллелограмм, у которого все углы прямые, называется прямоугольником.
Теоремы.
-
В параллелограмм можно вписать окружность тогда и только тогда, когда он является ромбом. -
Параллелограмм можно вписать в окружность тогда и только тогда, когда он является прямоугольником.
Четырехугольник, две стороны которого параллельны, а две - нет, называется трапецией.
Теоремы.
-
В трапецию можно вписать окружность тогда и только тогда, когда сумма боковых сторон равна сумме оснований. -
Около трапеции можно описать окружность тогда и только тогда, когда она равнобочная. -
В описанном около окружности четырехугольнике суммы противоположных сторон равны. В частности, если равнобочная трапеция описана около окружности, то ее средняя линия равна боковой стороне. -
Во вписанном в окружность четырехугольнике суммы противоположных углов равны .
1.5. Окружность и круг
Окружность – множество всех точек плоскости, равноудаленных от одной точки.
Хорда – отрезок, соединяющий две точки окружности.
Равные хорды окружности равноудалены от ее центра; равноудаленные от центра окружности хорды равны.
Диаметр – хорда, проходящая через центр.
Касательная – прямая, имеющая с окружностью одну общую точку.
Центральный угол – угол с вершиной в центре окружности.
Вписанный угол – угол с вершиной на окружности, стороны которого пересекают окружность.
Теоремы, относящиеся к окружности.
-
Радиус, проведенный в точку касания, перпендикулярен касательной. -
Диаметр, проходящий через середину хорды, перпендикулярен ей. -
Квадрат длины касательной равен произведению длины секущей на ее внешнюю часть. -
Центральный угол измеряется градусной мерой дуги, на которую он опирается. -
Вписанный угол измеряется половиной дуги, на которую он опирается, или дополняет его половину до 180. -
Касательные, проведенные к окружности из одной точки, равны. -
Произведение секущей на ее внешнюю часть – величина постоянная.
1.6. Основные формулы планиметрии
1. Произвольный треугольник (– стороны; –противолежащие им углы; - полупериметр; – радиус описанной окружности; – радиус вписанной окружности; – площадь; - высота, проведенная к стороне)
(теорема косинусов); (теорема синусов);.
2. Прямоугольный треугольник (– катеты; – гипотенуза; – проекции на гипотенузу)
;.
3. Равносторонний треугольник;; .
4. Произвольный выпуклый четырехугольник (и –диагонали, – угол между ними, – площадь)
5. Параллелограмм (и – смежные стороны, – угол между ними, – высота, проведенная к стороне ) ;; .
6. Ромб.
7. Прямоугольник .
8. Квадрат ( – диагональ) .
9. Трапеция (и – основания, – расстояние между ними, – средняя линия) ;.
10. Описанный многоугольник (– полупериметр, – радиус вписанной окружности) .
11. Правильный многоугольник (– сторона правильного – угольника, – радиус описанной окружности, – радиус вписанной окружности) .
12. Окружность, круг (– радиус, – длина окружности,– площадь круга) ;.
13. Сектор (– длина дуги, ограничивающей сектор, – градусная мера центрального угла, – радиальная мера центрального угла) ; .
§2. Решение задач и задач ЕГЭ с применением математического пакета Geogebra
2.1. Произвольный треугольник
Задача 1. Медианы треугольника ABC разрезают его на 6 треугольников. Докажите, что центры описанных окружностей этих треугольников лежат на одной окружности.
Создание чертежа. Пусть – медианы, – точка их пресечения
Шаги создания чертежа в GeoGebra (таб. 1):
Таблица 1
| № | Имя | Иконка GeoGebra | Определение |
| 1 | Треугольник |  | Произвольный треугольник, проходящий через точки . |
| 2 | Точка |  | Середины сторон треугольника соответственно. |
| 3 | Отрезки |  | Отрезки . |
| 4 | Точка |  | Точка пересечения прямых . |
| 5 | Окружность |  | Окружность через три точки . Так же строим и остальные окружности. |
| 6 | Прямая |  | Касательная к окружности в точке . |
| 7 | Прямая |  | Прямая через точку, перпендикулярная . |
| 8 | Точка |  | Точка пересечения прямой и окружности . |
| 7 | Точка–центр окружности |  | Середина отрезка (аналогично находятся и другие точки ). |
| 8 | Многоугольник |  | Шестиугольник, проходящий через точки . |
| 9 | Окружность |  | Окружность через любые три точки . |
Из чертежа (рис. 15) видно, центры описанных окружностей треугольниковлежат на одной окружности. Далее можно проводить доказательство.

Рис. 15
1 2 3 4 5 6 7