)^b] (51)

Распределение Пуассона.. Распределение дискретных случайных величин по закону распределения Пуассона. Например, если в начальный период эксплуатации изделия (период приработки) поток отказов нестационарный, то после окончания процесса приработки поток отказов становится стационарным и, следовательно, простейшим (пуассоновским).

Вероятность частот событий находят по формуле:

Р_m = = e^—a (52)

где m – частота данного события, mi – m – факториал, n –число испытаний, Р – вероятность события при одном испытании, а=nP – математическое ожидание случайных величин. Для распределения Пуассона дисперсия равна математическому ожиданию.
5.5 Критерии согласия.

При обработке эмпирических данных, чтобы иметь полное представление об изменениях случайной величины, надо знать закон ее распределения. Поэтому на основании экспериментальных данных выдвигают гипотезу о законе распределения случайной величины. Делают это обычно по величине коэффициента вариации υ. Если υ0,33 предлагают ЗНР, если υ0,50 – ЗРВ.

Смысл проверки «согласия» заключается в определении степени расхождения опытной и теоретической вероятности. Мерой совпадения или расхождения служат критерии согласия. Критерии согласия являются случайными величинами и, следовательно, подчиняются определенному закону распределения. Поэтому по величине критерия согласия и определяют вероятность совпадения опытной и теоретической функций. В качестве примера согласия в теории надежности пользуются двумя:

- Критерий Колмогорова -  определяю: = Dmax , (53)

где D_max – наибольшая абсолютная разность между накопленными эмпирическими и теоретическими частостями

D_max = , (54)

N – число наблюдений опытов.

По вычисленному  определяют вероятность Р() подчинения его закону распределения. В практических расчетах считается, что если  ≤ 1, то считают, что согласие между эмпирическим и теоретическим законами распределения хорошее. Более точно оценка согласия выполняется по функции вероятности Р(λ).

---

- Критерий Пирсона. При большом числе наблюдений сводит ошибки к минимуму. Он определяется из выражения:

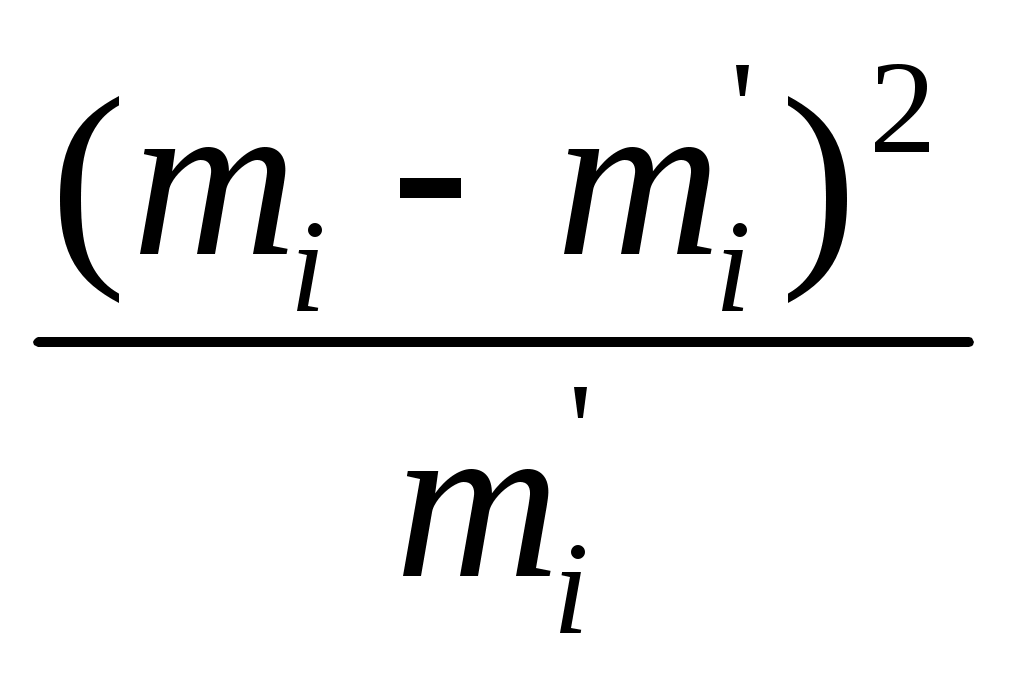= ∑ (55)

m_i – опытная частота (количество случаев) в i-м интервале статистического ряда; n_i – принятое количество интервалов; =N[F(t_i+1) – F(t_i)] – теоретическая частота.

Частоты, значение которых менее 5, следует объединить.

После нахождения определяем число степеней свободы:

K = n₁ – r – 1, (56)

где k – число степеней свободы; n_{1 –} число сравниваемых частот;

r – число параметров теоретической функции распределения.

5.6 Доверительная вероятность оценки точности определения математического ожидания и дисперсии.

Основные параметры теоретических распределений –математическое ожидание MX и дисперсия DX. Вычисленные по эмпирическому распределению среднее значение и дисперсия S² являются точечными оценками для теоретических значений MX и DX, и при достаточно большом числе опытов можно считать , что = MX , а S² = DX.. В связи с тем, что объем выборки , как правило, невелик, необходимо пользоваться интервальными оценками, которые определяются двумя числами – концами интервала. Интервальные оценки позволяют установить точность и надежность оценок, т.е. позволяют найти к каким ошибкам может привести замена значения теоретического параметра m статистической характеристикой m^*. Известно, что m^* тем точнее определяет параметр m, чем меньше абсолютная величина разности | m –m^* |, то есть δ> 0 и | m –m^* | <δ, чем меньше δ, тем оценка точнее. Таким образом ,положительное число δ характеризует точность оценки.

Однако статистические методы не позволяют категорически утверждать, что оценка m^* удовлетворяет неравенству | m –m^* | <δ, можно лишь говорить о вероятности α, при которой это неравенство справедливо.

Доверительной вероятностью (надежностью) оценки m по m^* называют вероятность α при которой выполняется неравенство | m –m

---

^* | <α.

Обычно надежность оценки задается наперед, в качестве α берут число, близкое к единице. Пусть вероятность того, что |m –m^*| <δ, равняется α;

P [| m –m^* | <δ ] = α, (57)

где δ заданная точность; α -достоверность оценки.

Отсюда: P [m^* - δ < m < m^* + δ] = α (58)

Это соотношение следует понимать так : вероятность того, что интервал (m^*-δ , m^*+ δ) заключает в себе(покрывает) неизвестный параметр m, равна α.

Доверительным интервалом I_α(Рисунок 10)называют интервал (m^*- δ, m^* + δ ) , который покрывает неизвестный параметр с заданной надежностью α.



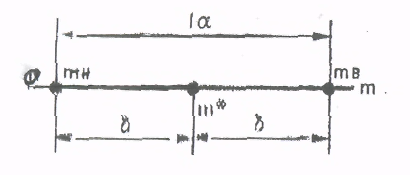
Рисунок 10. Доверительный интервал и доверительные границы.
Из рисунка 10 видно, что I_α = 2δ и характеризует точность оценки.

Интервал имеет случайные концы, которые называют доверительными границами. Доверительные границы сами являются случайными величинами, и зависят от величины выборки.

Доверительные интервалы для оценки математического ожидания нормального распределения могут определяться при известном и неизвестном среднеквадратическом отклонении σ. Если известна величина оценки m^* при известном σ, то верхнюю и нижнюю доверительные границы определяют по следующим уравнениям:

m_н = m^* - t (59)

m_в = m^* + t (60)

где t – число, которое определяется из равенства 2Ф(t) = α.

Из формулы δ = t σ/ следует, что при возрастании объема выборки n число δ убывает и, следовательно, точность оценки увеличивается.

Увеличение надежности оценки α приводит к увеличению t, а следовательно к возрастанию δ, т.е. увеличение надежности α влечет за собой уменьшение ее точности. Минимальный объем выборки, необходимый для оценки математического ожидания с заданной точностью δ и надежностью α находят по формуле:

n = (61)

Когда значение среднего квадратического отклонения неизвестно, вместо величины δ = t определяют величину

δ = t_у

---

(62)

где t _у – табличный коэффициент, определяемый для заданной доверительной вероятности α и числу степеней свободы k = n - 1; S – выборочная характеристика, определяемая по уравнению

S = (63)
Список рекомендуемой литературы

1.Д.Н.Решетов, А.С. Иванов Надежность машины М, Высшая школа, 1988.

2.В.И. Прейсман. Основы надежности техники. Киев «Вица школа», 1979.

3.Ермолов Л.С., Кряжков В.М., Черкун В.Е., - Основы надежности сельскохозяйственной техники. М.: Колос, 1982
Контрольные вопросы:

1.Какие законы распределения наиболее часто используются в теории надежности?

2. Что такое гистограмма и полигон распределения случайной величины?

3. По каким формулам определяются среднее арифметическое и среднее взвешенное?

4. Что такое медиана и мода?

5. Как определяется эмпирическое среднее квадратическое отклонение?

6. На основании какого параметра выдвигается гипотеза о законе распределения?

7. Что такое доверительный интервал и доверительные границы?

0>0>

---

Тема 7,8. Основные понятия и термины надежности техники. Количественные характеристики надежности.

Цель: Изучение понятий теории надежности технологических машин.

План:

1. Системы и элементы расчета.

2. Количественные характеристики надежности.

3. Показатели долговечности.

4. Показатели ремонтопригодности и сохраняемости.

5. Комплексные показатели надежности.
7.1 Системы и элементы расчета.

Квалиметрия – научная область, объединяющая количественные методы оценки качества, используемые для обоснования решений, принимаемых при управлении качеством продукции и стандартизации.

Показатели качества продукции – это количественная характеристика одного или нескольких ее свойств, составляющих качество. Этот показатель рассматривают применительно к условиям создания, эксплуатации или потребления продукции. Различают следующие показатели качества продукции.

Единичный показатель – показатель, характеризующий только одно свойство продукции.

Комплексный показатель – показатель, характеризующий несколько свойств продукции.

Интегральный показатель – отношение суммарного полезного эффекта от эксплуатации или потребления продукции к суммарным затратам на ее создание и эксплуатацию или потребление.

Оценка надежности технических объектов также возможна с помощью показателя надежности.

Показатель надежности – количественная характеристика одного или нескольких свойств, составляющих надежность технического объекта, т.е. он количественно характеризует, в какой степени конкретному объекту присущи определенные свойства, обуславливающие его надежность.

Для определения числовых значений надежности могут быть использованы как точные (теоретические), так и приближенные (статистические) уравнения.

Многие показатели надежности – это параметры распределения случайных величин. Для их оценки основными величинами, участвующими в расчетах, приняты следующие случайные величины; наработка, число отказов и число объектов, находящихся в эксплуатации или на испытаниях.

В соответствии с ГОСТ для количественной оценки надежности применяют единичные и комплексные показатели надежности.

Единичный показатель

---

Смотрите также файлы

• Какой внешний долг южной кореи.docx

• Особенности производства в отношении отдельных категорий лиц.docx

• Практическая работа 11 Управление системой компас3d цель приобрести навыки управления системой компас3d план.docx

• Студенты, чья фамилия начинается с букв аг, выполняют первый.docx

• Практическая работа 5 По дисциплине Физика Земли (наименование учебной дисциплины согласно учебному плану) Тема Выполнение геологической интерпретации фрагмента регионального геофизического профиля мовогт (геотраверса) Уралсейс.docx