Файл: В. Н. Коваленко надежность устройств железнодорожной автоматики, телемеханики и связи.doc

Напряжение питания триггера U_п = – 14 В.

№ вари­анта	3	7	9	11	14	15	18	19	22	23
t○C	30	50	55	60	65	50	45	35	40	60
Усло­вия экс­плуа­тации триг­гера	Ста­цио­нар­ные (поле­вые)	Кора­бель­ные	Авто­фур­гон­ные	Желез­нодо­рож­ные	Ста­цио­нар­ные (поле­вые)	Кора­бель­ные	Желез­нодо­рож­ные	Ста­цио­нар­ные (поле­вые)	Желез­нодо­рож­ные	Ста­цио­нар­ные (поле­вые)

Необходимо найти интенсивность отказа, вероятность безотказной работы и среднее время работы до первого отказа триггера, если отказы его элементов распределены по экспоненциальному закону:

- для лабораторных условий;

- для условий эксплуатации, согласно варианта.

Произвести анализ полученных результатов и дать рекомендации по повышению надёжности работы триггера.

3 РАСЧЕТ НАДЕЖНОСТИ НЕВОССТАНАВЛИВАЕМЫХ

РЕЗЕРВИРУЕМЫХ СИСТЕМ

3.1 Методы расчета

Резервирование – это метод повышения надежности объекта путем введения избыточности. Задача введения избыточности – обеспечить исправное функционирование системы после возникновения отказов в ее элементах. Резервирование может быть структурным, информационным и временным.

Структурное (аппаратное) резервирование предусматривает использование избыточных элементов.

Если резервирование применено к всей системе в целом, то такое резервирование называется общим, а если резервируются отдельные элементы или их группы – раздельным.

По схеме включения резервных элементов различают постоянное резервирование, резервирование замещением и скользящее резервирование.

В зависимости от режима работы резервных элементов различают нагруженный, облегченный и ненагруженный резервы.

Резервирование, при котором работоспособность любого основного или резервного элемента системы в случае возникновения отказов не подлежит восстановлению в процессе эксплуатации системы, называется резервированием без восстановления, а в противном случае имеет место резервирование с восстановлением.

---

Основным параметром резервирования является его кратность. Под кратностью резервирования m понимается отношение числа резервных элементов к числу резервируемых (основных). Различают резервирование с целой и дробной кратностью.

Основные расчетные формулы для определения количественных критериев различных видов резервирования приведены в /2,4/:

1. Общее резервирование с постоянно включенным резервом и целой кратностью определяется выражением

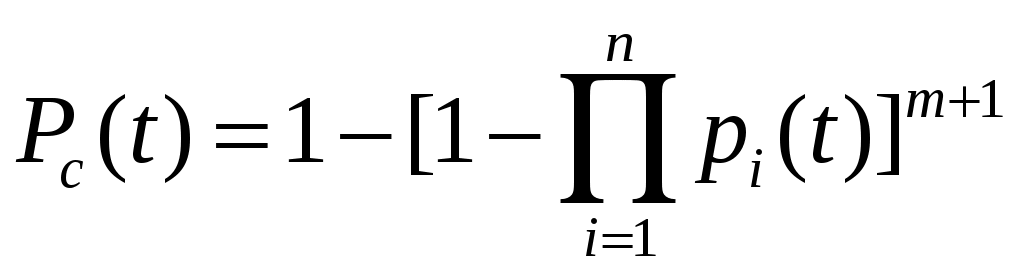, (3.1)

где n – число элементов основной или любой резервной цепи;

– вероятность безотказной работыi-го элемента в течение времениt;

m – кратность резервирования.

При экспоненциальном законе, когда
, (3.2)
где 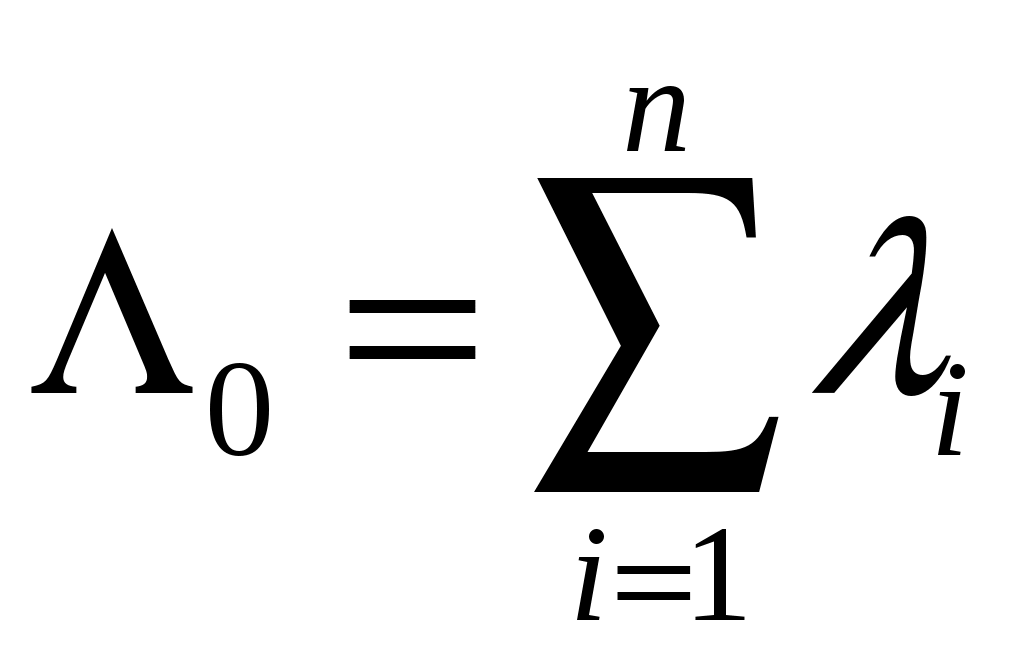– интенсивность отказов нерезервированной системы.

Среднее время безотказной работы резервированной системы
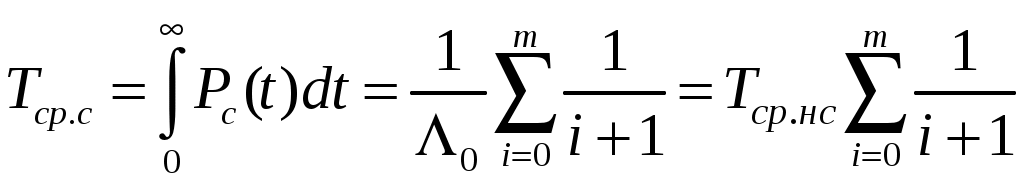, (3.3)
где - среднее время безотказной работы нерезервированной системы.

При резервировании неравнонадежных изделий вероятность безотказной работы определяется выражением
(3.4)
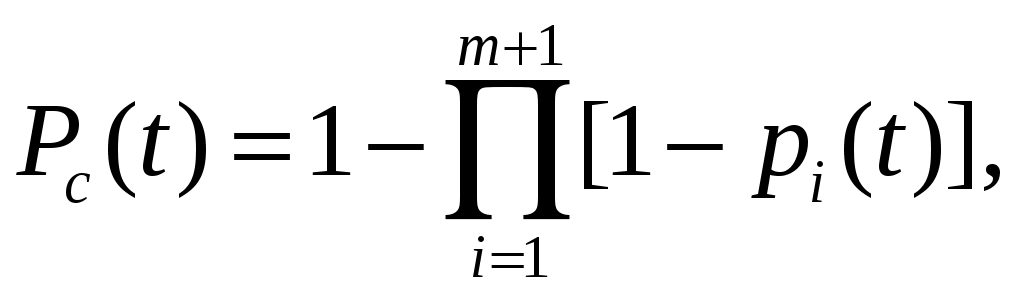
где – вероятность безотказной работы в течение времени t i-го изделия соответственно.

2. Раздельное резервирование с постоянно включенным резервом и с целой кратностью
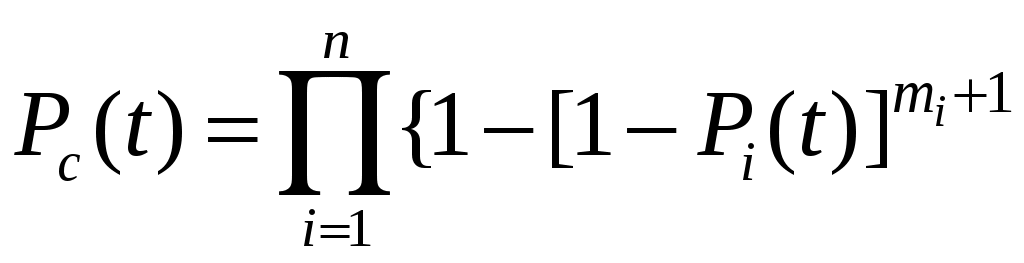, (3.5)
где n– число элементов основной системы;

– вероятность безотказной работы

---

i-го элемента;

– кратность резервирования i- го элемента.


При экспоненциальном законе надежности

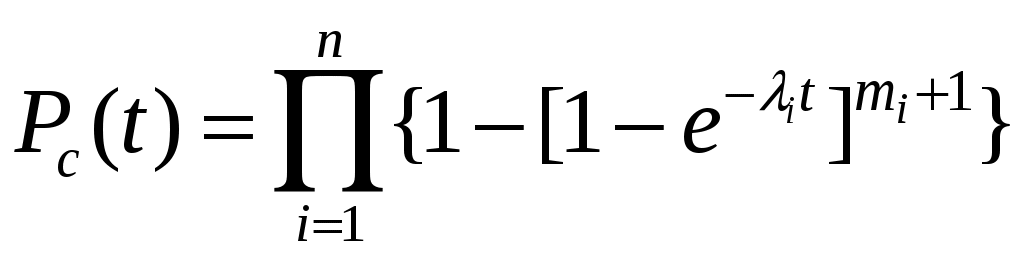. (3.6)
При использовании равнонадёжных элементов с одинаковой кратностью их резервирования
(3.7)
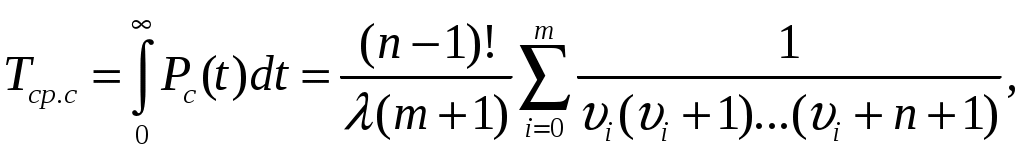(3.8)

где .
3. Общее резервирование замещением с целой кратностью
, (3.9)

где – вероятность безотказной работы резервированной системы кратности m+ 1 и m соответственно;

– вероятность безотказной работы основной системы в течении времени ;

– частота отказов резервированной системы кратности m в момент времени .

Рекуррентная формула (3.9) позволяет получить расчетные соотношения для устройства любой кратности резервирования. Для этого подставить вместо и их значения в соответствии с выбранным законом распределения и состоянием резерва и выполнить интегрирование в правой части.

При экспоненциальном законе распределения и ненагруженном резерве

(3.10)

где λ₀ – интенсивность отказов основной системы.
, (3.11)
где – средняя наработка до первого отказа основной системы.

---

При экспоненциальном законе и ненагруженном состоянии резерва
(3.12)
где ; - интенсивность отказов резервной системы до замещения.
(3.13)

где .

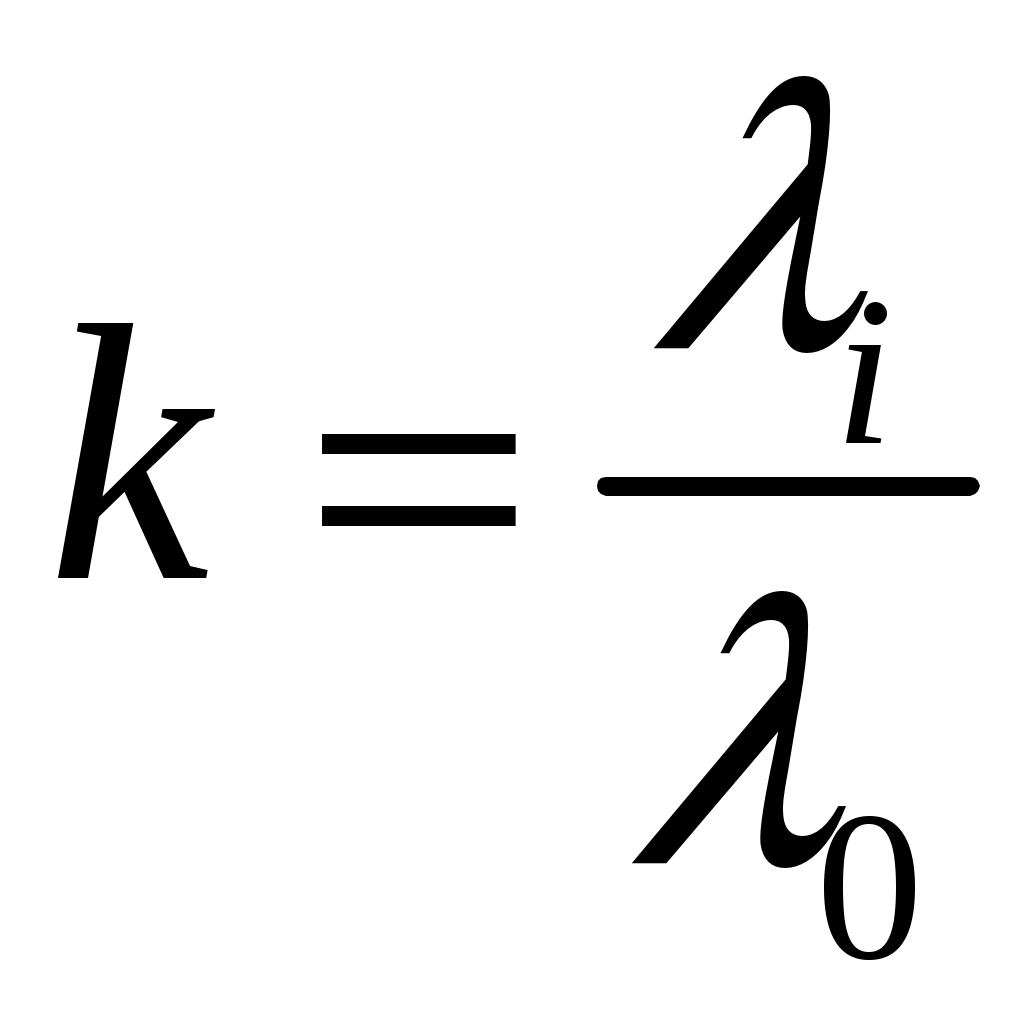При нагруженном состоянии резерва определяется выражением (3.2), – выражением (3.3).
4. Раздельное резервирование замещением с целой кратностью
(3.14)

где – вероятность безотказной работы системы из-за отказов элементов i-го типа, резервированных по способу замещения.

Вероятность безотказной работы вычисляется по формуле (3.9), (3.10) и (3.12).

5. Общее резервирование с дробной кратностью и постоянно включенным резервом

, (3.15)
где – вероятность безотказной работы основного или любого резервного элемента;

– число систем необходимых для нормальной работы резервированной системы;

l – общее число основных и резервных систем.
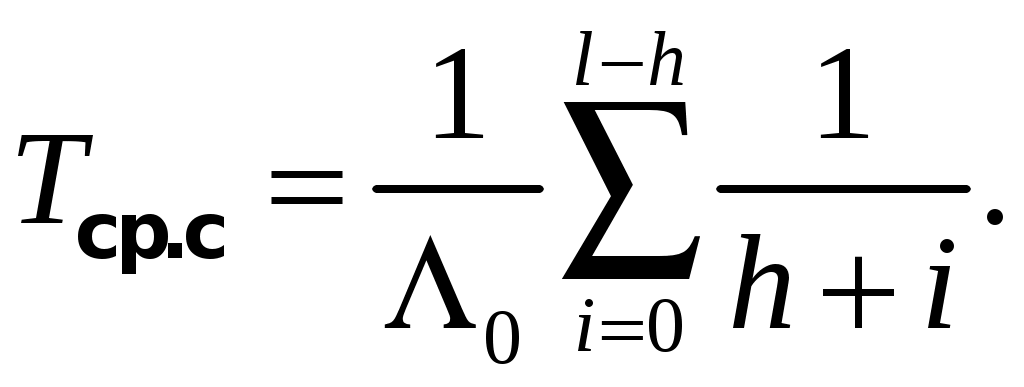(3.16)
Кратность резервирования для рассматриваемого случая
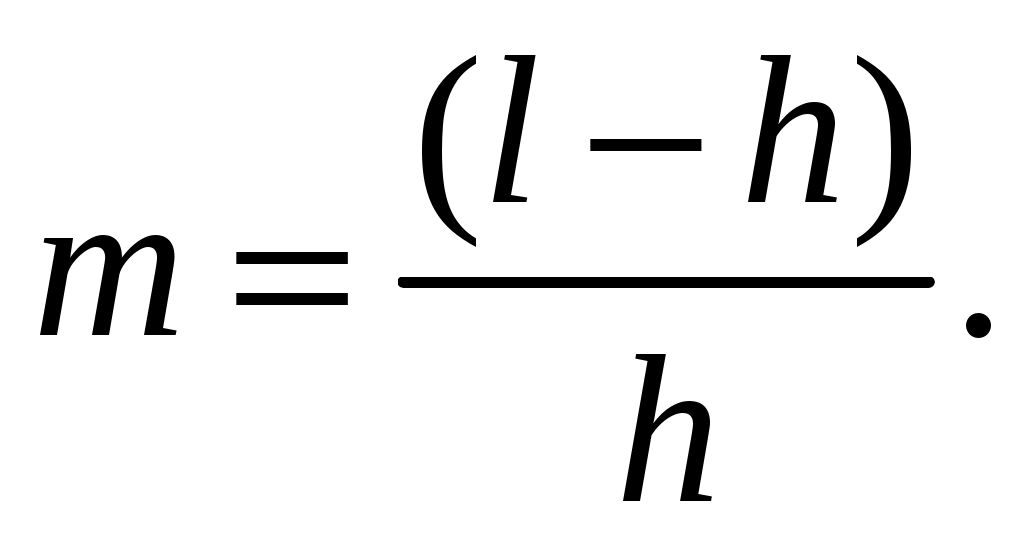
3.2 Типовые примеры

Пример 3.2.1.

---

В системе электроснабжения при профилактических работах, связанных с подготовкой электроустановок к работе зимой или для производства летних работ, многие электроустановки планово отключаются два раза в год. Требуется определить вероятность безотказной работы электрооборудования, функционирующего в режиме нагруженного дублирования, при лет, 1/год и t = 0,5 года среднее время до отказа.

Решение:

1. Определяем вероятность безотказной работы основного электрооборудования по выражению в течении времени t

2. Подставив полученное значение в формулу (3.1) получим



3. Среднее время работы электрооборудования до отказа по выражению (3.3)


3.3 Индивидуальные задания по теме «Расчет надежности

невосстанавливаемых резервируемых систем»

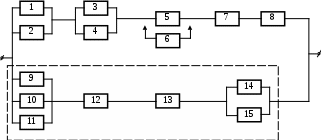
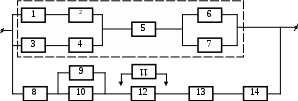
Задача 3.3.1. Задана структурная схема для расчета надежности системы (варианты структурных схем для расчета надежности системы представлены на рисунке 3.1), по известным интенсивностям отказов ее элементов (приведены в таблице 3.1) предполагая, что отказы элементов распределены по экспоненциальному закону. Определить:

- вероятность безотказной работы системы;

- интенсивность отказа узла системы (узлы на рисунке 3.1 обведены пунктиром);

- среднее время наработки до первого отказа узла системы.

На основе выполненного расчета представить график _узла(t), выводы и рекомендации по повышению надёжности заданной резервированной системы.



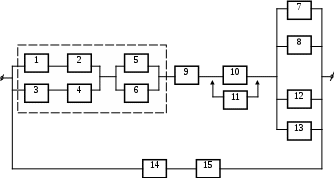
1

Рисунок 3.1, лист 1 Схемы надёжности невосстанавливаемых

резервированных систем


2


2

---