Файл: Эконометрические модели формирования финансовых активов кредитных организаций пфо.docx
Добавлен: 03.12.2023
Просмотров: 138
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Рисунок 2 – График остатков результативного признака
Вторая предпосылка относительно нулевой средней величины остатков тоже не выполняется, так как остатки на графике не лежат на одной прямой и выходят за границы допустимого «коридора», то есть случайное отклонение в среднем оказывает влияние на зависимую переменную и остатки зависимы от значений факторных признаков.
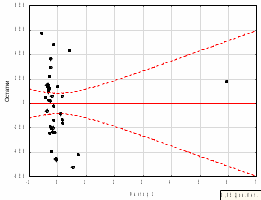
Рисунок 3 – График остатков факторного признака f1
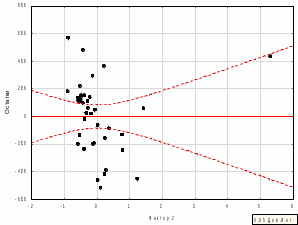
Рисунок 4 – График остатков факторного признака f2
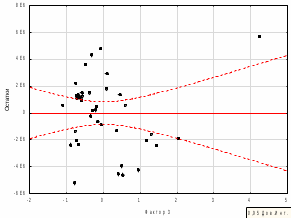
Рисунок 5 – График остатков факторного признака f3
Третья предпосылка о гомоскедастичной дисперсии остатков не выполняется. Если обратиться к рисунку 2, то мы можем увидеть, что дисперсия остатков неоднородна. Наблюдается гетероскедастичность.
Четвертая предпосылка – проверка остатков на отсутствие автокорреляции при помощи критерия Дарбина-Уотсона была выполнена.
Таблица 14 – Значение критерия Дарбина-Уотсона
При n=40 и k=3 нижняя граница dн=1,34 и верхняя граница dв=1,66. Отсюда получаем, что фактическое значение критерия Дарбина-Уотсона не попадает в зону неопределенности dн < DW < dв, соответственно, присутствует автокорреляция остатков.
Пятая предпосылка МНК о нормальном распределении остатков выполняется, так как распределение остатков подобно нормальному, что показывает построенный график нормального распределения.
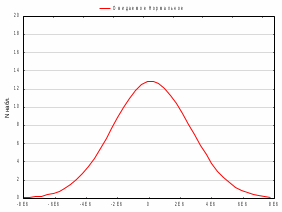
Рисунок 6 – График нормального распределения
Таким образом, было проведено исследование модели множественной линейной регрессии по пяти базовым условиям верификации и по пяти предпосылкам метода наименьших квадратов. Так как выполненными оказались все пять базовых условий верификации и выполнена одна последняя предпосылка МНК, можно сделать вывод, что данная модель регрессии подлежит применению на практике для решения исследуемой проблемы, но, чтобы построить достаточно точные дальние прогнозы о величины активов банков ПФО, модель нужно корректировать.
2.3 Построение системы эконометрических уравнений, характеризующих состояние финансовых активов кредитных организаций ПФО
Для построения системы уравнений финансовых активов кредитных организаций ПФО были рассмотрены следующие показатели:
y1 –активы-нетто (тыс. руб).;
y2 – капитал (тыс. руб.).;
Для проведения анализа используется следующие экзогенные переменные:
x1 – денежные средства в кассе, (тыс. руб);
х2 – ностро-счета, (тыс. руб);
х3 – выданные МБК, (тыс. руб);
х4 – вложения в ценные бумаги (тыс. руб);
х5 – кредиты физическим лицам, (тыс. руб);
х6 – кредиты предприятиям и организациям, (тыс. руб);
х7 – основные средства и нематериальные активы, (тыс. руб);
х8 – вклады физических лиц, (тыс. руб);
х9 – средства предприятий и организаций, (тыс. руб);
х10 – просроченная задолженность по кредитному портфелю, (тыс. руб).
Для описания структурных связей была построена СОУ, включающая 2 эндогенные переменные и 10 экзогенных переменных. При отборе переменных во избежание ошибок спецификации модели было принято во внимание то, что для выполнения условия статистической значимости и надежности результатов построения эконометрических моделей количество наблюдений в 3-6 раз должно превышать количество зависимых переменных (наблюдений 40)
Для построения системы был использован метод пошагового регрессионного анализа с включением в модель значимых регрессоров. Таким образом, в модели вошли только статистически значимые переменные. Полученная система имеет вид:
.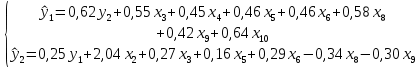
Для оценивания СОУ используется двухшаговый метод МНК. Он дает состоятельные и несмещенные оценки коэффициентов уравнения, является достаточно простым и удобным для вычисления. Использование 2МНК для оценивания структурных коэффициентов модели дает смещенные несостоятельные оценки. Поэтому для определения структурных коэффициентов структурная форма была преобразована в приведенную, которая ничем не отличается от системы независимых переменных, параметры которой оцениваются обычным МНК. Все два уравнения системы были преобразованы в приведенную форму:
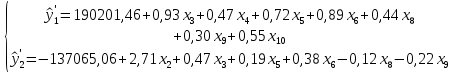
При переходе от приведенной формы модели к структурной возникает проблема идентификации.
Идентификация – единственность соответствия между приведенной и структурной формами модели.
Структурная модель всегда представляет собой систему совместных уравнений, каждое из которых требуется проверить на идентификацию. Для оценки параметров структурной модели система должна быть идентифицируема или сверхидентифицируема.
Первое уравнение включает 2 эндогенных переменных (y1, y2). В уравнении отсутствуют 3 экзогенных переменных (x1,x2,x7,). 3+1>1 (D+1>H). Значит уравнение сверхидентифицируемо.
Второе уравнение включает 2 эндогенные переменные (y1,y2). В уравнении отсутствуют 4 экзогенные переменные (x1,x4,x7x10). 4+1>3 (D+1>H). Значит уравнение сверхидентифицируемо.
Так как все уравнения сверхидентифицируемы, следовательно система сверхидентифицируема.
Рассмотренное счетное правило отражает необходимое, но не достаточное условие идентифицируемости. Более точное условие идентификации определяется, если накладывать ограничения на коэффициенты матрицы параметров структурной модели. Уравнение идентифицируемо, если по отсутствующим в нем переменным (эндогенным и экзогенным) можно из коэффициентов при них в других уравнения системы получить матрицу, определитель которой не равен нулю, а ранг матрицы не меньше, чем число эндогенных переменных в системе без одного. Поэтому каждое из уравнений было проверено на достаточное условие идентификации.
Составим матрицу коэффициентов структурной формы модели.
Таблица 15 – Матрица коэффициентов структурной формы модели.
В соответствии с достаточным условием идентификации определить матрицы коэффициентов при переменных, не входящих в исследуемое уравнение, не должен быть равен нулю, а ранг матрицы - числу эндогенных переменных минус 1, т.е. 2-1=1.
В первом уравнении матрица коэффициентов при переменных, не входящих в уравнение, имеет вид:
Ранг А1=1, т.к. определитель подматрицы 1х1 матрицы А1 не равен нулю (DefA1*=2,04) Достаточное условие идентификации для первого уравнения выполняется.
Во втором уравнении матрица коэффициентов при переменных, не входящих в уравнение, имеет вид:
Ранг А2=1, т.к. определитель подматрицы 1х1 матрицы А2 не равен нулю (DefA1*=0,45) Достаточное условие идентификации для первого уравнения выполняется.
Таким образом, для всех уравнений структурной формы выполняется достаточное условие идентифицируемости.
На основе системы приведенных уравнений были получены теоретические значения трех эндогенных переменных. Таким образом, система уравнений приняла следующий вид:
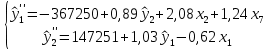
Ниже приведена таблица с итоговыми статистиками структурной формы системы эконометрических уравнений.
Таблица 16 – Итоговые статистики структурной формы
Можем заметить, что у первого уравнения коэффициент детерминации равен 0,999. Значение данного индекса близко к 1. Таким образом, вариация переменной y1 – стоимость активов банков на 99,9% объясняется вариацией факторов, включенных в модель. Остальные 0,1% приходятся на другие факторы, не учтенные в модели. Значение коэффициента детерминации второй модели равно 0,989. То есть вариация переменной у2 - капитал банков на 98,9% объясняется вариацией факторов, включенных в эту модель.
Коэффициенты корреляции первой модели составили 0,998, второй модели 0,979. Они отражают достаточно тесную связь результативного признака с набором факторных признаков. Точность моделей доказывалась с помощью расчета стандартной ошибки оценки. Ошибка первой и второй модели меньше, чем 10% значения от среднего значения результативного признака, поэтому модель признается точной (1025566,11<1624881,58); (753405,8<1624881,58). Рассчитанные наблюдаемые значения F-критерия Фишера в моделях, больше их табличных значений (3,7; 19,5) соответственно, поэтому уравнения в целом считаются статистически значимыми и надежными с уровнем значимости 95%.
Далее по модели регрессии рассматривались итоги регрессии для зависимой переменной.
Таблица 17 – Итоги регрессии для зависимой переменной Y1
Вторая предпосылка относительно нулевой средней величины остатков тоже не выполняется, так как остатки на графике не лежат на одной прямой и выходят за границы допустимого «коридора», то есть случайное отклонение в среднем оказывает влияние на зависимую переменную и остатки зависимы от значений факторных признаков.

Рисунок 3 – График остатков факторного признака f1

Рисунок 4 – График остатков факторного признака f2

Рисунок 5 – График остатков факторного признака f3
Третья предпосылка о гомоскедастичной дисперсии остатков не выполняется. Если обратиться к рисунку 2, то мы можем увидеть, что дисперсия остатков неоднородна. Наблюдается гетероскедастичность.
Четвертая предпосылка – проверка остатков на отсутствие автокорреляции при помощи критерия Дарбина-Уотсона была выполнена.
Таблица 14 – Значение критерия Дарбина-Уотсона
| | Дарбина - Уотсон d | Сериаль - Корр. |
| Оценка | 2,175024 | -0,131478 |
При n=40 и k=3 нижняя граница dн=1,34 и верхняя граница dв=1,66. Отсюда получаем, что фактическое значение критерия Дарбина-Уотсона не попадает в зону неопределенности dн < DW < dв, соответственно, присутствует автокорреляция остатков.
Пятая предпосылка МНК о нормальном распределении остатков выполняется, так как распределение остатков подобно нормальному, что показывает построенный график нормального распределения.

Рисунок 6 – График нормального распределения
Таким образом, было проведено исследование модели множественной линейной регрессии по пяти базовым условиям верификации и по пяти предпосылкам метода наименьших квадратов. Так как выполненными оказались все пять базовых условий верификации и выполнена одна последняя предпосылка МНК, можно сделать вывод, что данная модель регрессии подлежит применению на практике для решения исследуемой проблемы, но, чтобы построить достаточно точные дальние прогнозы о величины активов банков ПФО, модель нужно корректировать.
2.3 Построение системы эконометрических уравнений, характеризующих состояние финансовых активов кредитных организаций ПФО
Для построения системы уравнений финансовых активов кредитных организаций ПФО были рассмотрены следующие показатели:
y1 –активы-нетто (тыс. руб).;
y2 – капитал (тыс. руб.).;
Для проведения анализа используется следующие экзогенные переменные:
x1 – денежные средства в кассе, (тыс. руб);
х2 – ностро-счета, (тыс. руб);
х3 – выданные МБК, (тыс. руб);
х4 – вложения в ценные бумаги (тыс. руб);
х5 – кредиты физическим лицам, (тыс. руб);
х6 – кредиты предприятиям и организациям, (тыс. руб);
х7 – основные средства и нематериальные активы, (тыс. руб);
х8 – вклады физических лиц, (тыс. руб);
х9 – средства предприятий и организаций, (тыс. руб);
х10 – просроченная задолженность по кредитному портфелю, (тыс. руб).
Для описания структурных связей была построена СОУ, включающая 2 эндогенные переменные и 10 экзогенных переменных. При отборе переменных во избежание ошибок спецификации модели было принято во внимание то, что для выполнения условия статистической значимости и надежности результатов построения эконометрических моделей количество наблюдений в 3-6 раз должно превышать количество зависимых переменных (наблюдений 40)
Для построения системы был использован метод пошагового регрессионного анализа с включением в модель значимых регрессоров. Таким образом, в модели вошли только статистически значимые переменные. Полученная система имеет вид:
.
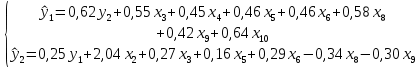
Для оценивания СОУ используется двухшаговый метод МНК. Он дает состоятельные и несмещенные оценки коэффициентов уравнения, является достаточно простым и удобным для вычисления. Использование 2МНК для оценивания структурных коэффициентов модели дает смещенные несостоятельные оценки. Поэтому для определения структурных коэффициентов структурная форма была преобразована в приведенную, которая ничем не отличается от системы независимых переменных, параметры которой оцениваются обычным МНК. Все два уравнения системы были преобразованы в приведенную форму:
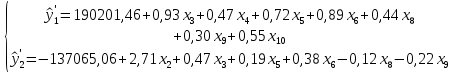
При переходе от приведенной формы модели к структурной возникает проблема идентификации.
Идентификация – единственность соответствия между приведенной и структурной формами модели.
Структурная модель всегда представляет собой систему совместных уравнений, каждое из которых требуется проверить на идентификацию. Для оценки параметров структурной модели система должна быть идентифицируема или сверхидентифицируема.
Первое уравнение включает 2 эндогенных переменных (y1, y2). В уравнении отсутствуют 3 экзогенных переменных (x1,x2,x7,). 3+1>1 (D+1>H). Значит уравнение сверхидентифицируемо.
Второе уравнение включает 2 эндогенные переменные (y1,y2). В уравнении отсутствуют 4 экзогенные переменные (x1,x4,x7x10). 4+1>3 (D+1>H). Значит уравнение сверхидентифицируемо.
Так как все уравнения сверхидентифицируемы, следовательно система сверхидентифицируема.
Рассмотренное счетное правило отражает необходимое, но не достаточное условие идентифицируемости. Более точное условие идентификации определяется, если накладывать ограничения на коэффициенты матрицы параметров структурной модели. Уравнение идентифицируемо, если по отсутствующим в нем переменным (эндогенным и экзогенным) можно из коэффициентов при них в других уравнения системы получить матрицу, определитель которой не равен нулю, а ранг матрицы не меньше, чем число эндогенных переменных в системе без одного. Поэтому каждое из уравнений было проверено на достаточное условие идентификации.
Составим матрицу коэффициентов структурной формы модели.
Таблица 15 – Матрица коэффициентов структурной формы модели.
| № ур-ия | Коэффициенты при эндогенных переменных | Коэффициенты при экзогенных переменных | ||||||||||
| y1 | y2 | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | |
| 1 | 1 | 0,62 | 0 | 0 | 0,55 | 0,45 | 0,46 | 0,46 | 0 | 0,58 | 0,42 | 0,64 |
| 2 | 0,25 | 1 | 0 | 2,04 | 0,27 | 0 | 0,16 | 0,29 | 0 | 0,34 | 0,3 | 0 |
В соответствии с достаточным условием идентификации определить матрицы коэффициентов при переменных, не входящих в исследуемое уравнение, не должен быть равен нулю, а ранг матрицы - числу эндогенных переменных минус 1, т.е. 2-1=1.
В первом уравнении матрица коэффициентов при переменных, не входящих в уравнение, имеет вид:
| А1 | 0 | 0 | 0 |
| 0 | 2,04 | 0 |
| DefA1* | 2,04 |
Ранг А1=1, т.к. определитель подматрицы 1х1 матрицы А1 не равен нулю (DefA1*=2,04) Достаточное условие идентификации для первого уравнения выполняется.
Во втором уравнении матрица коэффициентов при переменных, не входящих в уравнение, имеет вид:
| А2 | 0 | 0,45 | 0 | 0,64 |
| 0 | 0 | 0 | 0 |
| DefA1* | 0,45 |
Ранг А2=1, т.к. определитель подматрицы 1х1 матрицы А2 не равен нулю (DefA1*=0,45) Достаточное условие идентификации для первого уравнения выполняется.
Таким образом, для всех уравнений структурной формы выполняется достаточное условие идентифицируемости.
На основе системы приведенных уравнений были получены теоретические значения трех эндогенных переменных. Таким образом, система уравнений приняла следующий вид:
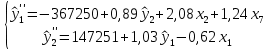
Ниже приведена таблица с итоговыми статистиками структурной формы системы эконометрических уравнений.
Таблица 16 – Итоговые статистики структурной формы
| № уравнения | Множест. R | Множест. R^2 | Скоррек. R^2 | F-статистика | p (уровень значимости) | Станд.ошибка проверки |
| 1 | 0,999 | 0,998 | 0,998 | 3787,05 | 0 | 1025566,11 |
| 2 | 0,989 | 0,979 | 0,977 | 845,91 | 0 | 753405,80 |
Можем заметить, что у первого уравнения коэффициент детерминации равен 0,999. Значение данного индекса близко к 1. Таким образом, вариация переменной y1 – стоимость активов банков на 99,9% объясняется вариацией факторов, включенных в модель. Остальные 0,1% приходятся на другие факторы, не учтенные в модели. Значение коэффициента детерминации второй модели равно 0,989. То есть вариация переменной у2 - капитал банков на 98,9% объясняется вариацией факторов, включенных в эту модель.
Коэффициенты корреляции первой модели составили 0,998, второй модели 0,979. Они отражают достаточно тесную связь результативного признака с набором факторных признаков. Точность моделей доказывалась с помощью расчета стандартной ошибки оценки. Ошибка первой и второй модели меньше, чем 10% значения от среднего значения результативного признака, поэтому модель признается точной (1025566,11<1624881,58); (753405,8<1624881,58). Рассчитанные наблюдаемые значения F-критерия Фишера в моделях, больше их табличных значений (3,7; 19,5) соответственно, поэтому уравнения в целом считаются статистически значимыми и надежными с уровнем значимости 95%.
Далее по модели регрессии рассматривались итоги регрессии для зависимой переменной.
Таблица 17 – Итоги регрессии для зависимой переменной Y1
| | БЕТА | Ст.Ош. | B | Ст.Ош. | t(33) | p-знач. |
| Св.член | | | -367250 | 236462,7 | -1,55310 | 0,129938 |
| Y^2 | 0,89 | 0,04 | 0,89 | 0,05 | 19,83 | 0,00 |
| X2 | 0,05 | 0,02 | 2,08 | 0,66 | 3,15 | 0,00 |
| X7 | 0,02 | 0,01 | 1,24 | 0,50 | 2,50 | 0,02 |
| X6 | -0,02 | 0,01 | -0,06 | 0,04 | -1,44 | 0,16 |
| X8 | 0,04 | 0,03 | 0,08 | 0,07 | 1,21 | 0,24 |
| X4 | 0,02 | 0,02 | 0,07 | 0,06 | 1,15 | 0,26 |