Файл: Эконометрические модели формирования финансовых активов кредитных организаций пфо.docx

Далее из исходной модели были исключены факторы с помощью пошагового метода с исключением в программе «Statistika».

Таблица итоговых статистик множественной модели регрессии представлена ниже.

Таблица 4 – Итоговые статистики модели регрессии

Показатели	Значение
Множест. R	0,998
Множест. R2	0,997
Скоррект. R2	0,997
F(5,34)	2408,67
p	2,55877100E-42
Стд. Ош. Оценки	1407730,35

Таким образом, условие достаточности количества наблюдений было выполнено, так как уравнение множественной регрессии было построено по 40 наблюдениям, данное число превышало число объясняющих переменных. Модель более качественна, если коэффициент детерминации приближен к единице. Видим, что у данной модели коэффициент детерминации равен 0,998. Значение данного индекса стремится к 1. Таким образом, вариация переменной y – активы банков ПФО на 99,8% объясняется вариацией пяти факторов. Остальные 0,2% приходятся на другие факторы, не учтенные в модели. Коэффициент корреляции составил 0,997. Связь прямая, сильная, так как находится в соответствующем диапазоне от 0,7 до 1. Точность модели доказывалась с помощью расчета стандартной ошибки оценки. Ошибка была равна 1407730,35, она меньше, чем значение 16248816 – 10% от среднего значения результативного признака, поэтому модель признается точной. Рассчитанное наблюдаемое значение F-критерия Фишера при степенях свободы 5 и 35 составило 2408,67, оно больше его табличного значения 4,4, поэтому уравнение в целом считается статистически значимым и надежным с уровнем значимости 95%.

Далее была построена таблица с итогами регрессии для зависимой переменной регрессионной модели.

Таблица 5 – Итоги регрессии для зависимой переменной регрессионной модели

	БЕТА	Ст.Ош.	B	Ст.Ош.	t(34)	p-знач.
Св.член			77105,70	303434,54	0,25	0,80
x3	0,48	0,02	1,09	0,05	22,23	0,000000000
x4	0,23	0,03	0,65	0,10	6,57	0,000000157
x5	0,13	0,02	0,85	0,11	7,54	0,000000009
x6	0,29	0,02	1,09	0,06	17,91	0,000000000
x8	0,16	0,05	0,34	0,10	3,34	0,002049119

---

В результате осталось 5 наиболее значимых факторных признаков: x₃ – выданные МБК, (тыс. руб); x₄ – вложения в ценные бумаги (тыс. руб); x₅ – кредиты физическим лицам, (тыс. руб); x₆ – кредиты предприятиям и организациям, (тыс. руб); x₈ – вклады физических лиц, (тыс. руб).

Проверка статистической значимости и надежности параметров уравнения регрессии, проверялось на основании t-критерия Стьюдента. Все параметры регрессии оказались статистически значимыми и надежными с уровнем значимости 95% , так как их наблюдаемые значения коэффициента по модулю больше табличного значения 2,032. Таким образом, условие было выполнено.

Зависимость активов банков ПФО от пяти факторных признаков можно описать следующим уравнением регрессии:

---

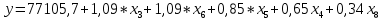
На основании бета-коэффициентов мы можем сделать вывод о силе влияния факторов на результативный признак. Наиболее сильное влияние на сумму активов банков оказывает два фактора x₃ – выданные МБК и x₆ – кредиты предприятиям и организациям. Наименьшее влияние оказывает фактор x₈ – вклады физических лиц. Также можем сделать вывод, что при увеличении суммы выданных межбанковских кредитов и суммы выданных кредитов предприятиям и организациям на 1 тыс. руб, активы банков будут увеличиваться на 1,09 тыс. руб. При увеличении суммы кредитов физическим лицам на 1 тыс. руб, активы банков будут увеличиваться на 0,85 тыс. руб. Также можно сказать, что сумма активов банков ПФО увеличится на 0,65 тыс. руб, если сумма кредитов предприятиям и организациям увеличится на 1 тыс. руб. А при увеличении суммы вкладов физических лиц в банках ПФО на 1 тыс. руб, сумма активов банков увеличится на 0,34 тыс. руб.

При получении двух различных моделей в ходе применения методов пошаговой гребневой регрессии предпочтение будет отводиться той модели, которая проиллюстрирует меньшие потери информационной значимости в соответствии с информационными критериями Акаике, Шварца.

Информационный критерий Акаике:

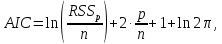(1)

где RSS_p – сумма квадратов остатков модели,

n – объем выборки,

p – количество факторов, включенных в модель.

Критерий Шварца:

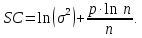(2)

Для модели с включеним критерий Акаике = 33,64, а исключением = 32,67. Критерий Шварца для модели с включением = 29,57, а для модели и исключением 28,64. Таким образом, наименьшие информационные потери несет построение множественной регрессии с помощью модели с исключением.

Можно казать, что рассматривая в конечном итоге модель с исключением в результате, остается 5 наиболее значимых факторных признаков: x₃ – выданные МБК, (тыс. руб); x₄ – вложения в ценные бумаги (тыс. руб); x₅ – кредиты физическим лицам, (тыс. руб); x₆ – кредиты предприятиям и организациям, (тыс. руб); x₈ – вклады физических лиц, (тыс. руб). А на основании бета-коэффициентов мы можем сделать вывод о силе влияния факторов на результативный признак. Наиболее сильное влияние на сумму активов банков оказывает два фактора x

---

₃ – выданные МБК и x₆ – кредиты предприятиям и организациям. Наименьшее влияние оказывает фактор x₈ – вклады физических лиц.

2.2 Построение эконометрической модели по главным компонентам и регрессионный анализ
Метод главных компонент (компонентный анализ) является частным случаем анализа факторного. Именно поэтому он позволяет решать тот же круг задач, связанный с «сужением» признакового пространства; описанием совокупности объектов наблюдения непосредственно не измеряемыми, но объективно существующими интегральными характеристиками – главными компонентами; выявлением взаимосвязи наблюдаемых признаков с вновь полученными обобщающими показателями; прогнозировании изучаемого явления с помощью уравнения регрессии на главных компонентах и др.

Так как в 2.1 мы выяснили, что изучаемые нами факторные признаки являются мультиколлинеарными, то есть присутствует линейная зависимость между объясняющими переменными. При помощи метода главных компонент попробуем избавиться от мультиколлинеарности при помощи объединения взаимосвязанных переменных в один фактор.

Для проведения факторного анализа были взяты 40 банковских кредитных организаций Приволжского Федерального Округа, которые имеют лицензию, то есть специальное разрешение на осуществление банковской деятельности, выдаваемое юридическому лицу. В ней указываются разрешенные операции, валюта их осуществления, номер и дата выдачи. Был исключен ПАО «АкБарс» Банк. Это объясняется тем, что данная банковская кредитная организация имеет высокие финансовые показатели, что во многом различаются от остальных. В основу исследования легли следующие показатели.

В качестве результативного признака был взят показатель активы-нетто, в единицах измерения тыс. руб. Было выбрано десять факторных признаков, тем или иным образом влияющих на активы банка, а именно:

x₁ – денежные средства в кассе, (тыс. руб);

х₂ – ностро-счета, (тыс. руб);

х₃ – выданные МБК, (тыс. руб);

х₄ – вложения в ценные бумаги (тыс. руб);

х₅ – кредиты физическим лицам, (тыс. руб);

х₆ – кредиты предприятиям и организациям, (тыс. руб);

х₇ – основные средства и нематериальные активы

---

, (тыс. руб);

х₈ – вклады физических лиц, (тыс. руб);

х₉ – средства предприятий и организаций, (тыс. руб);

х₁₀ – просроченная задолженность по кредитному портфелю, (тыс. руб);

На основании приведенных данных, был проведен факторный анализ в системе Statistica с применением метода главных компонент.

Целью факторного анализа является объединение факторов в несколько факторных компонентов для снижения размерности данных. Отбор главных компонент происходил по следующим критериям:

- проценту накопленных дисперсий первых нескольких компонент;

- собственным числам главных компонент;

- графическому методу.

Анализ начался с рассмотрения собственных значений независимых переменных.

Таблица 6 – Собственные значения главных компонент

Значение	Собств. Знач.	% общей - дисперс.	Кумулятивн. - Собств. Знач.	Кумулятивн. - %
1	5,57	55,71	5,57	55,71
2	2,03	20,31	7,60	76,02
3	1,02	10,25	8,63	86,27

Видим, что собственные значения трех компонент допустимые, они больше единицы. Коэффициент кумулятивности первого фактора = 56%, второго фактора = 76%, третьего фактора 86%.

Ниже представлен график каменистой осыпи, который показывает, что осыпание первых трех компонент происходит наиболее существенно, поэтому мы можем взять данные компоненты в дальнейшее рассмотрение.

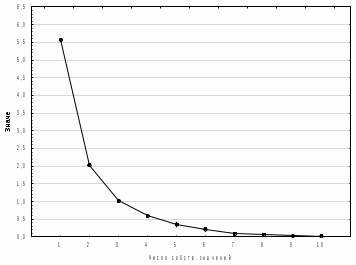Рисунок 1 – График собственных значений

Рассмотрим, какими факторами нагружена каждая полученная компонента. Эти факторы определяются, исходя из их значений коэффициентов корреляции больше 0,7.
Таблица 7 – Факторные нагрузки без вращения

	Фактор - 1	Фактор - 2	Фактор - 3
x1	-0,76	0,17	-0,39
x2	-0,89	-0,09	0,18
x3	-0,81	-0,54	0,04
x4	-0,83	-0,44	0,15
x5	-0,43	0,25	-0,79
x6	-0,645	0,63	0,30
x7	-0,56	0,62	-0,01
x8	-0,95	-0,09	-0,08
x9	-0,89	-0,41	0,08
x10	-0,47	0,70	0,31

---