Файл: Дрістер жинаы (15 саат) etn (II) 2216 Электр техниканы теориялы негіздері (II).doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 157
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
және 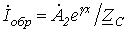 .
.
(8) мен (9) негізінде түзу және кері толқындар үшін кернеу мен ток Ом заңы бойынша орындалады
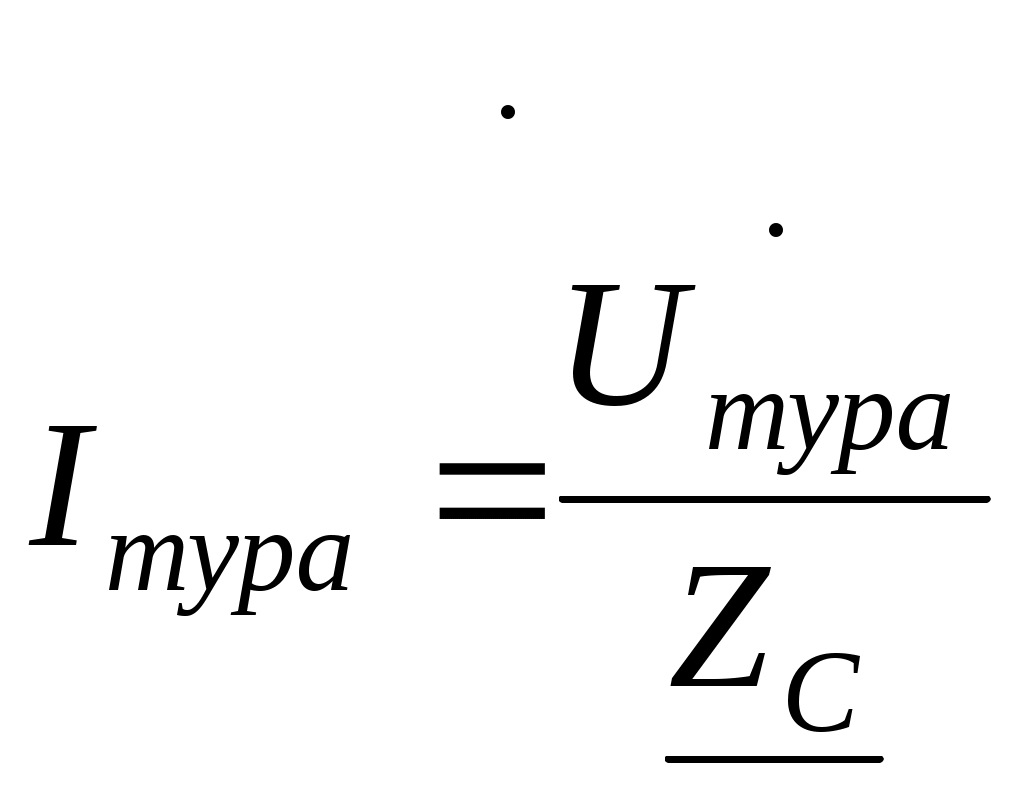 ,
, 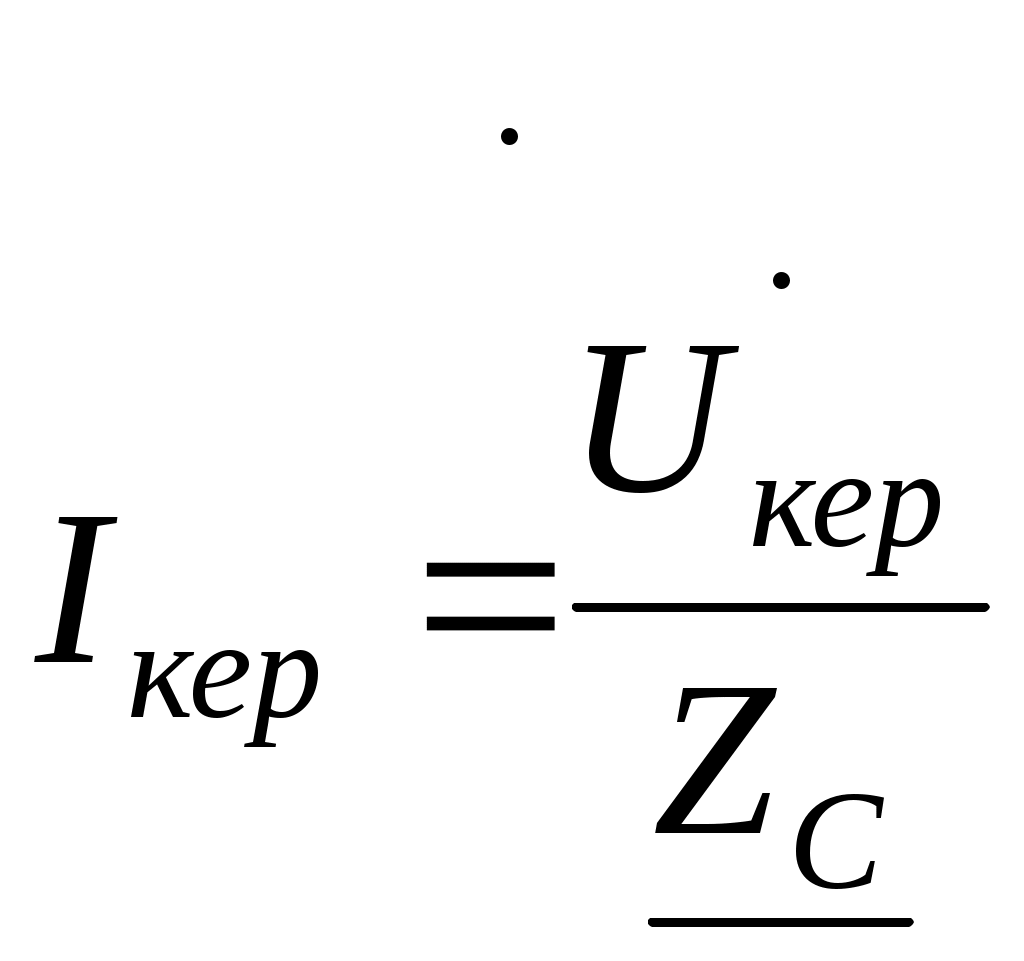
№13 дәріс 13. Желінің кіріс кедергісі. Гиперболалы фукнциялы біртекті сызықтың теңдеуі.
13.1 Желінің кіріс кедергісі.
Ұзын желінің кіріс кедергісі деп (тармақталған көрсеткішті тізбектерде) желінің таратқыш қысқыштарынның орнына қосылған соңғысының жұмыс ережесін өзгертпейтін шоғырланған кедергілер айтылады.
Жалпы жағдайда ерікті жүктемелі желінің кіріс кедергісі үшін былай жазуға болады:
Алынған өрнек кіріс кедергінің және , оның ұзындығы және жүктемелікөрсеткіштері бар функция болып табылатынын көрсетеді. Сонымен бірге, кіріс кедергінің желі ұзындығына тәуелділігі , яғни функциясы монотонды емес, бірақ кері толқынның (шағылдырғыш) әсерімен шарттасқан тербелмелі сипатты ұстайды. Желі ұзындығы төмендеген сайын тура, сәйкесінше шағылдырғыш толқындар күштірек өшеді. Нәтижесінде соңғысының әсері әлсіреп, тербеліс амплитудасының функциясы кемиді. Келісілен жүктемеде, яғни болған кезде, жоғарыда көрсетілгендей, кері толқын болмайды, ол толығымен (13.1) өрнекке сай келеді, кезінде мына қатынасқа трансформацияланады:
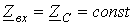 .
.
Дәл осы шамамен кезінде кіріс кедергісі анықталады.
Түзу ұзындығының кейбір мәндерінде оның кіріс кедергісі таза активті болуы мүмкін. заттық болған желі ұзындығын резонансты деп атайды. Шоғырланған көрсеткішті тізбектердегідей резонанс шығын жоқ кезде анық байқалады. Шығынсыз желілер үшін (13.1) негізінде жазуға болады.
13.2 Гиперболалы фукнциялы біртекті сызықтың теңдеуі.
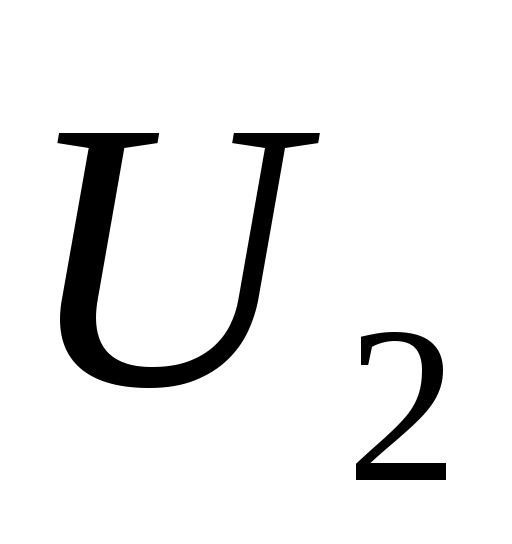 кернеу мен
кернеу мен 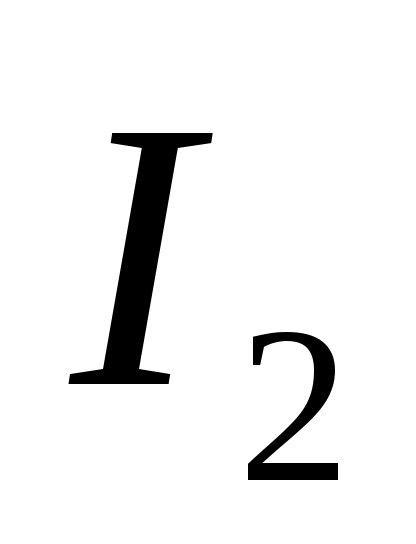 тогы бар мүшелерді топтастырып, (13.5) теңдеуін жазамыз:
тогы бар мүшелерді топтастырып, (13.5) теңдеуін жазамыз:
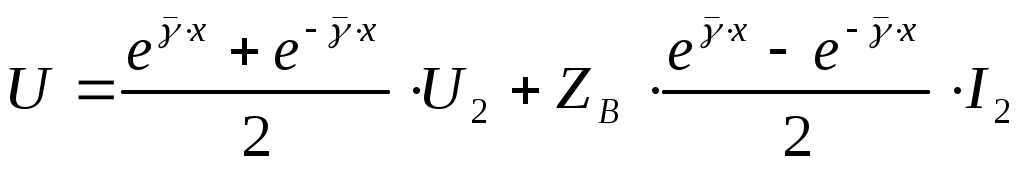 ,
,
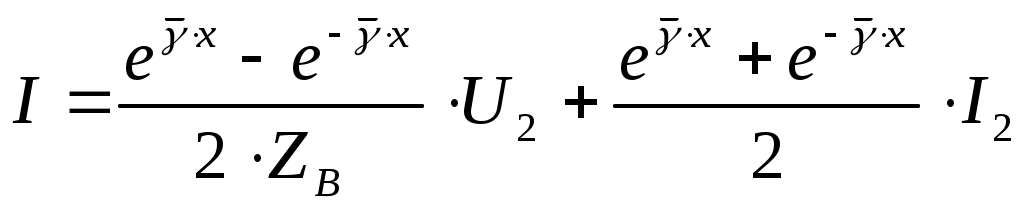 ,
,
Бірақ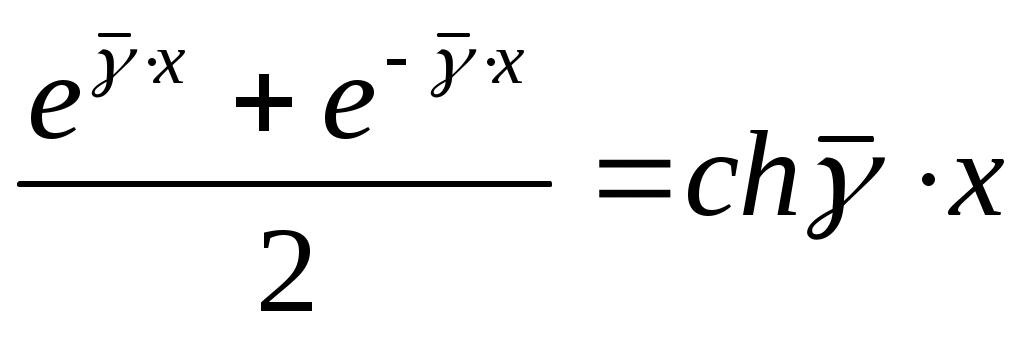 ,
,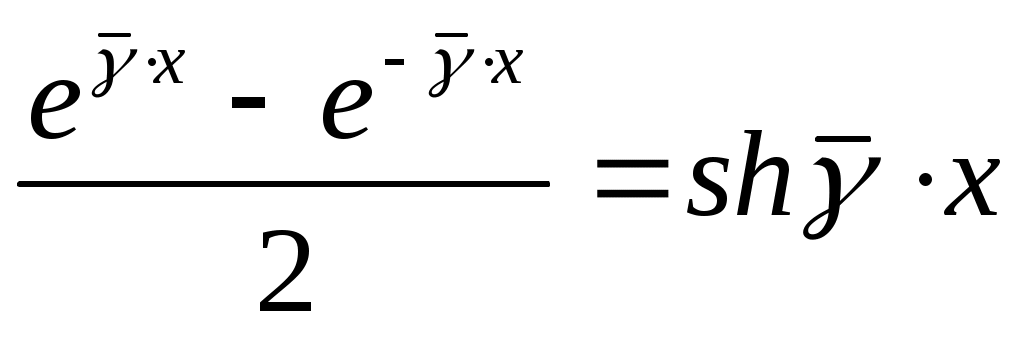 . (13.5)
. (13.5)
(13.5) теңдеуін ескерсек, қалыптасқан синусоидалы режим кезінде ұзын желінің теңдеуі келесі түрде болады:
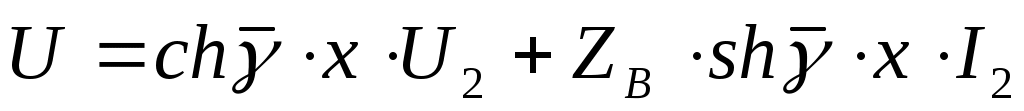 ,
,
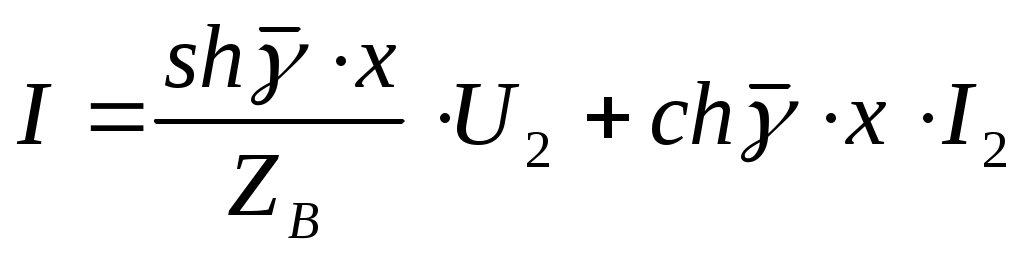 (13.6)
(13.6)
Егер желінің кірісінде ток пен кернеуді табу керек болса, яғни ,
, 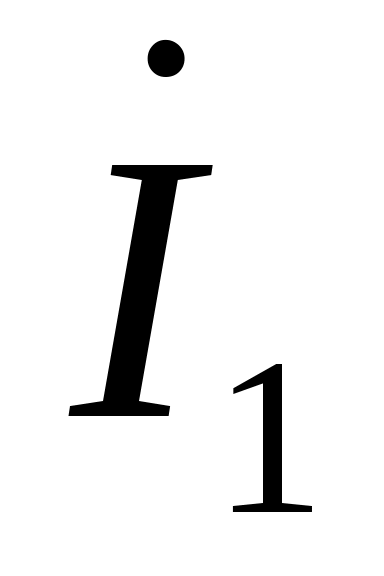 , онда бұл теңдеулерге
, онда бұл теңдеулерге 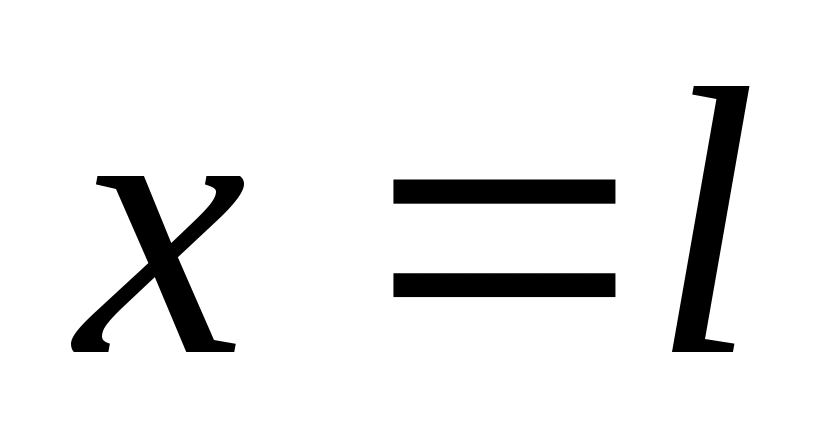 қою керек.
қою керек.
№14 дәріс 14. Толқынның шағылу коэффициенті. Желідегі келісілген жүктемесі.
14.1 Желідегі келісілген жүктемесі.
Толқындық кедергіге жүктелген ұзын желінің жұмыс ережесі келісілген деп аталады, ал желінің өзі келісілген жүктемелі желі деп аталады.
Келісілген жүктеме толығымен желі соңына жеткен толқын қуатын жұтады. Бұл қуат – натурал деп аталады. Кез келген келісілген желі қиылысуында кедергі толқындық кедергіге тең болғандықтан, кернеу мен тоқ арасындағы жылжу бұрышы өзгермейді. Сондықтан, генератордан алынған желі қуаты -ге тең болса, онда осы жағдай үшін ұзындықты желі соңындағы қуат
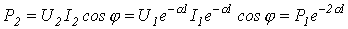 ,
,
бұдан желінің ПӘЕ-сі
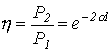
және өшуі
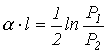 .
.
Төртұштықтарды қарастырғанда қуат бойынша сәйкес есе, ал кернеу мен ток бойынша рез өшетін өшудің бірлігі непер екені көрсетілді.
№15 дәріс 15. Шығынсыз желі. Бос жүріс, қысқа тұйықталу және шығынсыз желілердің жүктемелік режимі.
15.1 Шығынсыз желі
Шығынсыз желі деп бастапқы көрсеткіштері мен 0-ге тең болатын желіні айтамыз. Бұл жағдайда, жоғарыда көрсетілгендей, және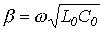 . Сондықтан,
. Сондықтан,
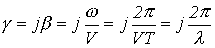 ,
,
бұдан .
кешенді аргументінен гиперболалық функцияларды ашайық.
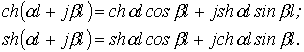
Онда шығынсыз желі үшін, кезінде мына қатынастардың мәні бар:
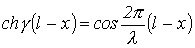 және
және 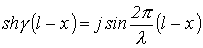
Сол себептен, шығынсыз желілер үшін кешенді аргументтен гиперболалық функциядағы ұзын желі теңдеулері, заттық аргументтің шеңберлік тригонометриялық функциялар қатысымен жазылған теңдеулерге трансформацияланады.
Қысқа айтқанда, шығынсыз желі (шығынсыз көрсеткішті тармақталған тізбек) идеалды жағдайды көрсетеді. Бірақ ,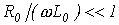 және
және 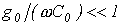 шарты орындалғанда, мысалы үлкен жиілікті тізбектер үшін мағызы бар, желі – шығынсыз желі деп есептеуге болады, бұдан оны (15.1 және (15.2)-шы теңдеулер арқылы сипаттауға болатыны шығады.
шарты орындалғанда, мысалы үлкен жиілікті тізбектер үшін мағызы бар, желі – шығынсыз желі деп есептеуге болады, бұдан оны (15.1 және (15.2)-шы теңдеулер арқылы сипаттауға болатыны шығады.
15.2 Бос жүріс, қысқа тұйықталу және шығынсыз желілердің жүктемелік режимі.
Бос жүріс (БЖ) және қысқаша тұйықталу (ҚТ) ережелері үшін (15.3)-тен, жүктемемен қолданылатын активті қуат 0-ге тең, сәйкесінше алатынымыз:
Желінің ұзындығына тәуелді өзгеру сипаттамасының (15.3) негізінде зерттелуі , кезінде модулі бойынша шегі аралығында өзгеретінін және сыйымдылық сипатын көрсетеді, ал - кезінде шегі аралығында өзгереді және индуктивті сипаттамаға ие. Мұндай кезек алмасу толқын ұзындығының (1а, сурет) төрттен біріне тең түзу ұзындығының кесіндісінен кейін де жалғасады.
Толқынның төрттен біріне тең жылжумен сәйкес сипаттама ҚТ кезінде ( 1б, сурет) тәуелділігіне ие болады.
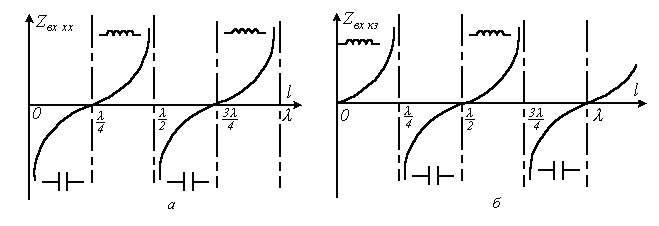
15.1 Сурет
нүктелері кернеу резонансына , нүктелері ток резонансына сәйкес келеді.
Сол себептен, шығынсыз желінің ұзындығын өзгерте отырып, кез келген шаманың сыйымдылық және индуктивті кедергілерін имитациялауға болады. Толқын ұзындығы жиіліктің функциясы болғандықтан, -ке сай өзгеруін желі ұзындығының өзгеруімен емес, генератор жиілігін өзгертумен жасауға болады. Тек кейбір жиіліктерде тармақталған көрсеткіштері тізбектегі кіріс кедергі – заттық (вещественный) бола алады. Мұндай жиіліктер
резонансты деп аталады.
15.3 Желі төртұштық түрінде.
Т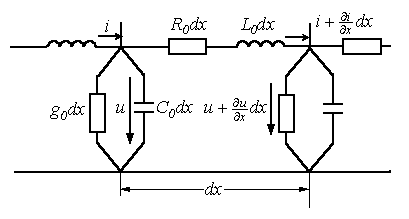 армақталған көрсеткіштері бар тізбектердегі кезеңдерді зерттеу үшін (басқа атауы – ұзын сызық), оның көрсеткіштері сызығының маңында біркелкілік таралу қосымша шартын енгіземіз: индуктивтіліктің, кедергінің, сыйымдылық пен өткізгіштіктің.
армақталған көрсеткіштері бар тізбектердегі кезеңдерді зерттеу үшін (басқа атауы – ұзын сызық), оның көрсеткіштері сызығының маңында біркелкілік таралу қосымша шартын енгіземіз: индуктивтіліктің, кедергінің, сыйымдылық пен өткізгіштіктің.
Мұндай сызықты – біртекті деп атайды. Көрсеткіштері біркелкі емес таратылған сызықтарды көпшілік жағдайда біркелкі бөліктерге бөлуге болады.
15.1 Сурет
Ұсынылған әдебиеттер тізімі
Негізгі әдебиеттер:
5. Сборник задач по теоретическим основам электротехники/ Л.Д.Бессонов, И.Г.Демидова, М.Е.Заруди и др.-М.: Высшая школа, 2003.-52с.
6. Прянишников В.А. ТОЭ: Курс лекций: Учебное пособие – 3-е изд., перераб. и доп. – СПб., 2012 – 368 с.
Қосымша әдебиеттер:
7. Аршидинов М.М. Электротехниканың теориялық негіздері.-А., 2003
8. Демирчян К.С., Нейман Л.Р., Коровкин Н.В., Чечурин В.Л. Теоретические основы электротехники. Т.1. - СПб.: Питер, 2003.-463с.
9. Электротехника и электроника в экспериментах и упражнениях: Практикум на Electronics Workbench. В 2-х томах/ Под ред. Д.И. Панфилова – М.: ДОДЭКА, 1999.- т.1-Электротехника. – 304с.
10.Бессонов Л.А. Теоретические основы электротехники.-М.: Гардарики,1999. - 638с.
11. Шебес М.Р., Каблукова М.В. Задачник по теории линейных электрических цепей. - М.: Высшая школа, 1990.- 544с.
12. Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей.- М.: Энергоатомиздат, 1989. -528с.
Мазмұны
1 Дәріс 1.…...……....................…………………..………......2
2 Дәріс 2…………………………………………....................5
3 Дәріс 3…...………………………….………..................….9
4 Дәріс 4...……………………………………........................11
5 Дәріс 5….…………………........……………......................14
6 Дәріс 6….……………………………....………...................20
(8) мен (9) негізінде түзу және кері толқындар үшін кернеу мен ток Ом заңы бойынша орындалады
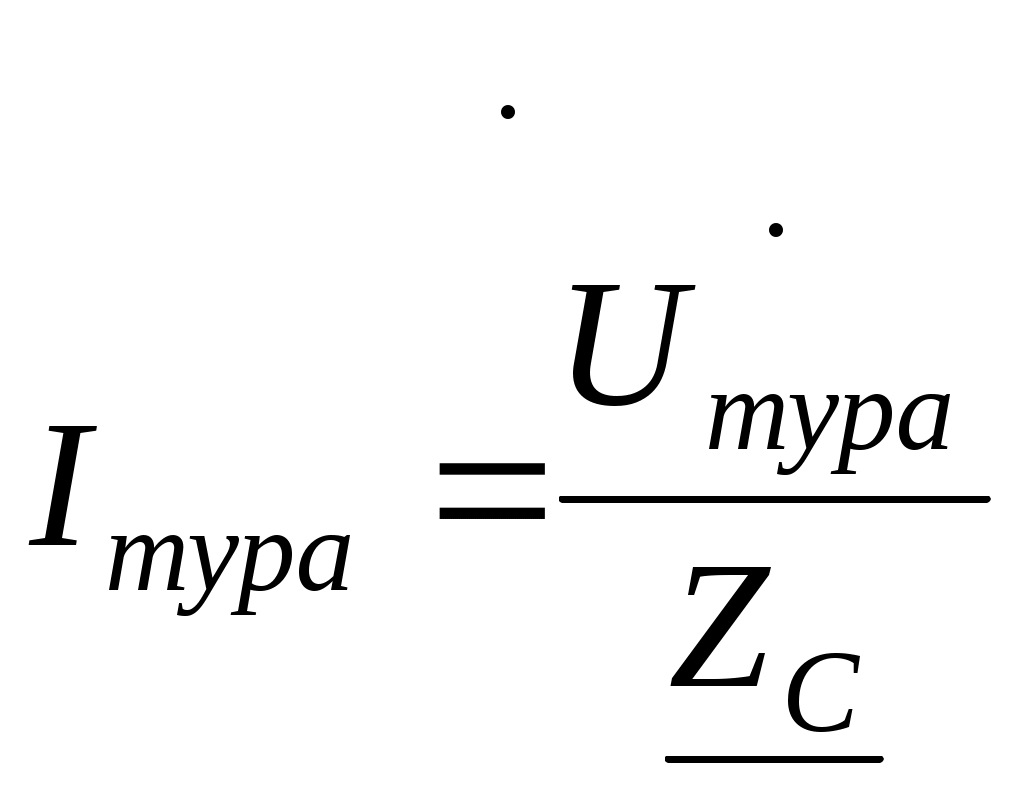 ,
, 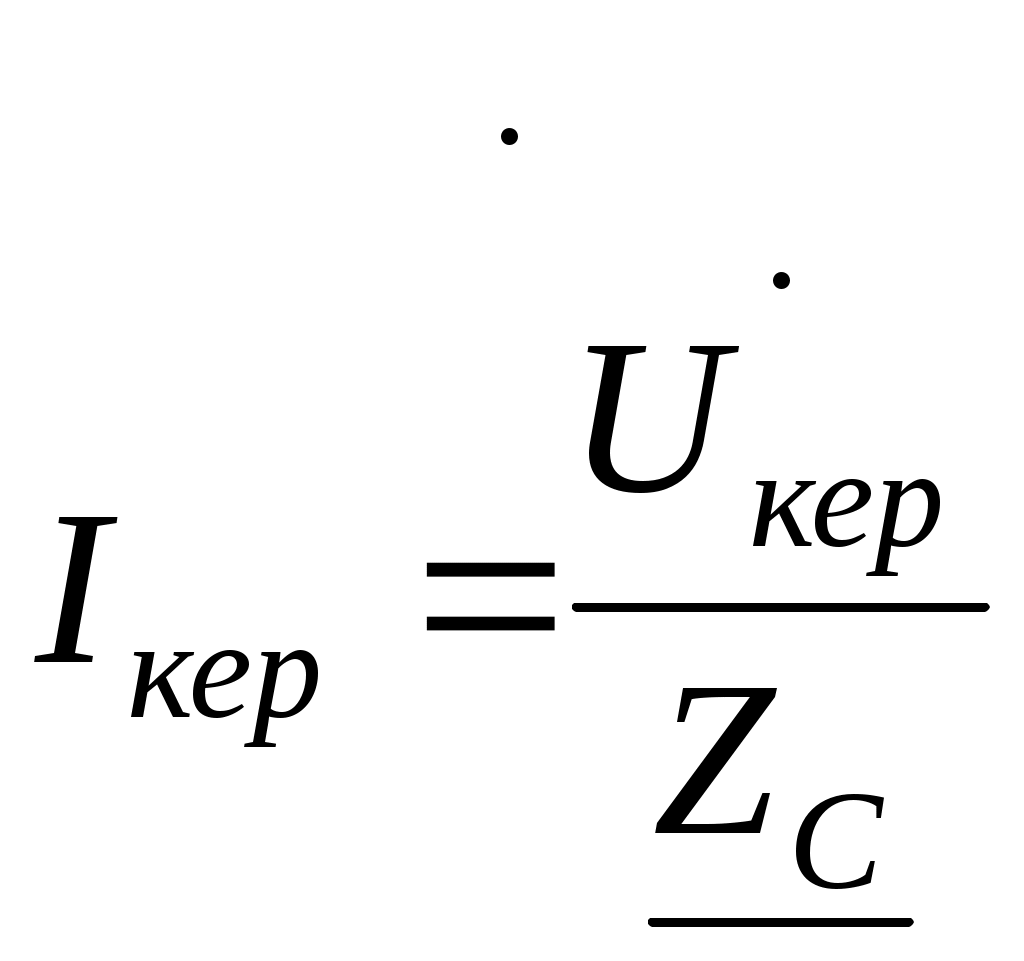
№13 дәріс 13. Желінің кіріс кедергісі. Гиперболалы фукнциялы біртекті сызықтың теңдеуі.
13.1 Желінің кіріс кедергісі.
Ұзын желінің кіріс кедергісі деп (тармақталған көрсеткішті тізбектерде) желінің таратқыш қысқыштарынның орнына қосылған соңғысының жұмыс ережесін өзгертпейтін шоғырланған кедергілер айтылады.
Жалпы жағдайда ерікті жүктемелі желінің кіріс кедергісі үшін былай жазуға болады:
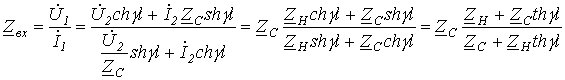 | (13.1 |
Алынған өрнек кіріс кедергінің және , оның ұзындығы және жүктемелікөрсеткіштері бар функция болып табылатынын көрсетеді. Сонымен бірге, кіріс кедергінің желі ұзындығына тәуелділігі , яғни функциясы монотонды емес, бірақ кері толқынның (шағылдырғыш) әсерімен шарттасқан тербелмелі сипатты ұстайды. Желі ұзындығы төмендеген сайын тура, сәйкесінше шағылдырғыш толқындар күштірек өшеді. Нәтижесінде соңғысының әсері әлсіреп, тербеліс амплитудасының функциясы кемиді. Келісілен жүктемеде, яғни болған кезде, жоғарыда көрсетілгендей, кері толқын болмайды, ол толығымен (13.1) өрнекке сай келеді, кезінде мына қатынасқа трансформацияланады:
Дәл осы шамамен кезінде кіріс кедергісі анықталады.
Түзу ұзындығының кейбір мәндерінде оның кіріс кедергісі таза активті болуы мүмкін. заттық болған желі ұзындығын резонансты деп атайды. Шоғырланған көрсеткішті тізбектердегідей резонанс шығын жоқ кезде анық байқалады. Шығынсыз желілер үшін (13.1) негізінде жазуға болады.
13.2 Гиперболалы фукнциялы біртекті сызықтың теңдеуі.
Бірақ
(13.5) теңдеуін ескерсек, қалыптасқан синусоидалы режим кезінде ұзын желінің теңдеуі келесі түрде болады:
Егер желінің кірісінде ток пен кернеуді табу керек болса, яғни
№14 дәріс 14. Толқынның шағылу коэффициенті. Желідегі келісілген жүктемесі.
14.1 Желідегі келісілген жүктемесі.
Толқындық кедергіге жүктелген ұзын желінің жұмыс ережесі келісілген деп аталады, ал желінің өзі келісілген жүктемелі желі деп аталады.
Келісілген жүктеме толығымен желі соңына жеткен толқын қуатын жұтады. Бұл қуат – натурал деп аталады. Кез келген келісілген желі қиылысуында кедергі толқындық кедергіге тең болғандықтан, кернеу мен тоқ арасындағы жылжу бұрышы өзгермейді. Сондықтан, генератордан алынған желі қуаты -ге тең болса, онда осы жағдай үшін ұзындықты желі соңындағы қуат
бұдан желінің ПӘЕ-сі
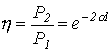
және өшуі
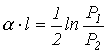 .
.Төртұштықтарды қарастырғанда қуат бойынша сәйкес есе, ал кернеу мен ток бойынша рез өшетін өшудің бірлігі непер екені көрсетілді.
№15 дәріс 15. Шығынсыз желі. Бос жүріс, қысқа тұйықталу және шығынсыз желілердің жүктемелік режимі.
15.1 Шығынсыз желі
Шығынсыз желі деп бастапқы көрсеткіштері мен 0-ге тең болатын желіні айтамыз. Бұл жағдайда, жоғарыда көрсетілгендей, және
бұдан .
кешенді аргументінен гиперболалық функцияларды ашайық.
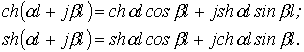
Онда шығынсыз желі үшін, кезінде мына қатынастардың мәні бар:
Сол себептен, шығынсыз желілер үшін кешенді аргументтен гиперболалық функциядағы ұзын желі теңдеулері, заттық аргументтің шеңберлік тригонометриялық функциялар қатысымен жазылған теңдеулерге трансформацияланады.
| | (15.1 |
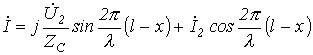 | 15.2 |
Қысқа айтқанда, шығынсыз желі (шығынсыз көрсеткішті тармақталған тізбек) идеалды жағдайды көрсетеді. Бірақ ,
15.2 Бос жүріс, қысқа тұйықталу және шығынсыз желілердің жүктемелік режимі.
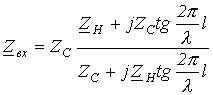 | (15.3) |
Бос жүріс (БЖ) және қысқаша тұйықталу (ҚТ) ережелері үшін (15.3)-тен, жүктемемен қолданылатын активті қуат 0-ге тең, сәйкесінше алатынымыз:
| | (15.4) |
| | (15.5) |
Желінің ұзындығына тәуелді өзгеру сипаттамасының (15.3) негізінде зерттелуі , кезінде модулі бойынша шегі аралығында өзгеретінін және сыйымдылық сипатын көрсетеді, ал - кезінде шегі аралығында өзгереді және индуктивті сипаттамаға ие. Мұндай кезек алмасу толқын ұзындығының (1а, сурет) төрттен біріне тең түзу ұзындығының кесіндісінен кейін де жалғасады.
Толқынның төрттен біріне тең жылжумен сәйкес сипаттама ҚТ кезінде ( 1б, сурет) тәуелділігіне ие болады.
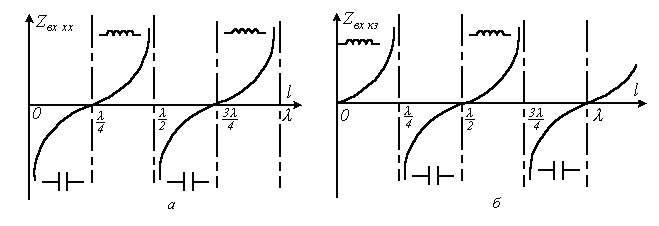
15.1 Сурет
нүктелері кернеу резонансына , нүктелері ток резонансына сәйкес келеді.
Сол себептен, шығынсыз желінің ұзындығын өзгерте отырып, кез келген шаманың сыйымдылық және индуктивті кедергілерін имитациялауға болады. Толқын ұзындығы жиіліктің функциясы болғандықтан, -ке сай өзгеруін желі ұзындығының өзгеруімен емес, генератор жиілігін өзгертумен жасауға болады. Тек кейбір жиіліктерде тармақталған көрсеткіштері тізбектегі кіріс кедергі – заттық (вещественный) бола алады. Мұндай жиіліктер
резонансты деп аталады.
15.3 Желі төртұштық түрінде.
Т
 армақталған көрсеткіштері бар тізбектердегі кезеңдерді зерттеу үшін (басқа атауы – ұзын сызық), оның көрсеткіштері сызығының маңында біркелкілік таралу қосымша шартын енгіземіз: индуктивтіліктің, кедергінің, сыйымдылық пен өткізгіштіктің.
армақталған көрсеткіштері бар тізбектердегі кезеңдерді зерттеу үшін (басқа атауы – ұзын сызық), оның көрсеткіштері сызығының маңында біркелкілік таралу қосымша шартын енгіземіз: индуктивтіліктің, кедергінің, сыйымдылық пен өткізгіштіктің.Мұндай сызықты – біртекті деп атайды. Көрсеткіштері біркелкі емес таратылған сызықтарды көпшілік жағдайда біркелкі бөліктерге бөлуге болады.
15.1 Сурет
Ұсынылған әдебиеттер тізімі
Негізгі әдебиеттер:
-
Аршидинов М.М., Нурова А.И. ЭТН-3. Электр тізбектерін және электрмагнитті өрістерді есептеу. №1-5 есептеу-графикалық жұмыстарға әдістемілік нұскаулар мен тапсырмалар. Алматы: АЭжБУ, 2012, 23 б. -
Аршидинов М.М., Бекеева А.Н. Электротехниканың теориялық негіздері 3. Электр тізбектердегі өтпелі және орнатылған режимдерді зерттеу. – Алматы, 2012, 30бет -
Әміров Ж.Х., Аршидинов М.М. Электротехниканың теориялық негіздері –3 /Оқулық құрал/. Алматы: АЭжБИ, 2008, 111 б. -
Аршидинов М.М., Әміров Ж.Х. Электротехниканың теориялық негіздері –1,2./Оқулық құрал/. Алматы: АЭжБИ, 2006, 170 б.
5. Сборник задач по теоретическим основам электротехники/ Л.Д.Бессонов, И.Г.Демидова, М.Е.Заруди и др.-М.: Высшая школа, 2003.-52с.
6. Прянишников В.А. ТОЭ: Курс лекций: Учебное пособие – 3-е изд., перераб. и доп. – СПб., 2012 – 368 с.
Қосымша әдебиеттер:
7. Аршидинов М.М. Электротехниканың теориялық негіздері.-А., 2003
8. Демирчян К.С., Нейман Л.Р., Коровкин Н.В., Чечурин В.Л. Теоретические основы электротехники. Т.1. - СПб.: Питер, 2003.-463с.
9. Электротехника и электроника в экспериментах и упражнениях: Практикум на Electronics Workbench. В 2-х томах/ Под ред. Д.И. Панфилова – М.: ДОДЭКА, 1999.- т.1-Электротехника. – 304с.
10.Бессонов Л.А. Теоретические основы электротехники.-М.: Гардарики,1999. - 638с.
11. Шебес М.Р., Каблукова М.В. Задачник по теории линейных электрических цепей. - М.: Высшая школа, 1990.- 544с.
12. Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей.- М.: Энергоатомиздат, 1989. -528с.
Мазмұны
1 Дәріс 1.…...……....................…………………..………......2
2 Дәріс 2…………………………………………....................5
3 Дәріс 3…...………………………….………..................….9
4 Дәріс 4...……………………………………........................11
5 Дәріс 5….…………………........……………......................14
6 Дәріс 6….……………………………....………...................20