Файл: Предмет аналитической химии.doc

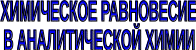
3.1. Общая характеристика химического равновесия. Константа химического равновесия

Большинство химических реакций, использующихся в аналитической химии, можно считать обратимыми. Протекание обратимой химической реакции в закрытой системе приводит к установлению химического равновесия.

Все химические равновесия характеризуются соответствующими константами химического равновесия. Выражение для константы химического равновесия можно получить, используя термодинамический или кинетический подход. Рассмотрим вначале идеальный случай, когда химическая реакция протекает в идеальном растворе - гипотетической системе, в которой взаимодействия между всеми компонентами одинаковы и не зависят от природы частиц. Пусть имеется следующее химическое равновесие

aA + bB  cC + dD

В состоянии равновесия

, следовательно

= 0

Так как

, находящаяся в левой части полученного уравнения, является постоянной величиной, то и произведение, стоящее в правой части этого уравнения - также постоянная величина.

Отношение произведения концентраций находящихся в состоянии равновесия продуктов химической реакции, взятых в степенях, равных их стехиометрическим коэффициентам, к соответствующему произведению равновесных концентраций реагирующих веществ называется константой химического равновесия (К)

3.2. Активность и коэффициент активности

Несмотря на то, что термодинамика не учитывает процессы,

происходящие в реальных растворах, например, притяжение и отталкивание ионов, термодинамические закономерности, выведенные для идеальных растворов, можно применить и для реальных растворов, если заменить концентрации активностями.
Активность (a) - такая концентрация вещества в растворе, при использовании которой свойства данного раствора могут быть описаны теми же уравнениями, что и свойства идеального раствора.
Активность может быть как меньше, так и больше номинальной концентрации вещества в растворе. Активность чистого растворителя, а также растворителя в не слишком концентрированных растворах принимается равной 1. За 1 принимается также активность твёрдого вещества, находящегося в осадке, или жидкости, не смешивающейся с данным раствором. В бесконечно разбавленном растворе активность растворённого вещества совпадает с его концентрацией.

Отношение активности вещества в данном растворе к его концентрации называется коэффициентом активности.

Коэффициент активности - это своеобразный поправочный коэффициент, показывающий, насколько реальность отличается от идеала.

3.3. Отклонения от идеальности в растворах сильных электролитов
Особенно заметное отклонение от идеальности имеет место в растворах сильных электролитов. Это отражается, например, на их температурах кипения, плавления, давлении пара над раствором и, что особенно важно для аналитической химии, на величинах констант различных равновесий, протекающих в таких растворах.
Для характеристики активности электролитов используют:

Для электролита A_mB_n:

Величина, которая учитывает влияние концентрации (С) и заряда (z) всех ионов, присутствующих в растворе, на активность растворённого вещества, называется

ионной силой (I).

Пример 3.1. В 1,00 л водного раствора содержится 10,3 г NaBr, 14,2 г Na₂SO₄ и 1,7 г NH₃. Чему равна ионная сила такого раствора?

0,100 моль/л

0,100 моль/л

С(Na⁺) = 0,300 моль/л, С(Br^-) = 0,100 моль/л, С(SO₄^2-) = 0,100моль/л

I = 0,5[0,300(+1)² + 0,100(-1)² + 0,100(-2)²] = 0,400 моль/л

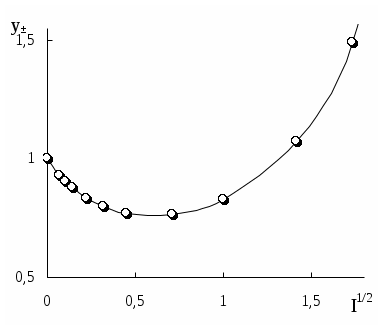
Рис. 3.1. Влияние ионной силы на среднеионный коэффициент активности HCl

На рис. 3.1 показан пример влияния ионной силы на активность электролита (HCl). Аналогичная зависимость коэффициента активности от ионной силы наблюдается также у HClO₄, LiCl, AlCl₃ и многих других соединений. У некоторых электролитов (NH₄NO₃, AgNO₃) зависимость коэффициента активности от ионной силы является монотонно убывающей.

Универсального уравнения, с помощью которого можно было бы рассчитать коэффициент активности любого электролита при любой величине ионной силы, не существует. Для описания зависимости коэффициента активности от ионной силы в очень разбавленных растворах (до I < 0,01) можно использовать предельный закон Дебая-Хюккеля

где A - коэффициент, зависящий от температуры и диэлектрической проницаемости среды; для водного раствора (298К) A  0,511.

Данное уравнение было получено голландским физиком П. Дебаем и его учеником Э. Хюккелем исходя из следующих предположений. Каждый ион был представлен в виде точечного заряда (т.е. размер иона не учитывался), окружённого в растворе ионной атмосферой - областью пространства сферической формы и определённого размера, в которой содержание ионов противоположного знака по отношению к данному иону больше, чем вне её. Заряд ионной атмосферы равен по величине и противоположен по знаку заряду создавшего её центрального иона. Между центральным ионом и окружающей его ионной атмосферой существует электростатическое притяжение, которое стремится стабилизировать данный ион. Стабилизация приводит к понижению свободной энергии иона и уменьшению его коэффициента активности. В предельном уравнении Дебая-Хюккеля природа ионов не учитывается. Считается, что при малых значениях ионной силы коэффициент активности иона не зависит от его природы.

При увеличении ионной силы до 0,01 и больше предельный закон начинает давать всё большую и большую погрешность. Это происходит потому, что реальные ионы имеют определённый размер, вследствие чего их нельзя упаковать так плотно, как точечные заряды. При увеличении концентрации ионов происходит уменьшение размеров ионной атмосферы. Так как ионная атмосфера стабилизирует ион и уменьшает его активность, то уменьшение её размера приводит к менее значительному уменьшению коэффициента активности.

Для расчёта коэффициентов активности при ионных силах порядка 0,01 - 0,1 можно использовать расширенное уравнение Дебая-Хюккеля:

где B  0,328 (T = 298K, a выражено в ), a - эмпирическая константа, характеризующая размеры ионной атмосферы.

При более высоких значениях ионной силы (до 1) количественную оценку коэффициента активности можно проводить по уравнению Дэвиса.

В данном уравнении a принято равным 3,05, поэтому произведение Ba равно 1. Фактор 0,2I учитывает образование ионных пар, изменение диэлектрической проницаемости и т.д.

В ещё более концентрированных растворах начинают сильно проявляться индивидуальные особенности ионов, поэтому уравнения, описывающего экспериментальные данные для таких растворов, нет. У одних электролитов коэффициент активности уменьшается, что может быть обусловлено образованием ионных пар, у других он увеличивается - за счёт уменьшения не принимающих участие в гидратации молекул воды и по другим причинам.

Пример 3.2. Рассчитать коэффициенты активности иона H⁺ при ионной силе 0,010 и 0,10.

При I = 0,010