Файл: Индивидуальное домашнее задание по дискретной математике.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 331
Скачиваний: 21
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Индивидуальное домашнее задание по дискретной математике
-
Справедливо ли в общем случае утверждение: если АВ и ВС и СD то АD? -
Может ли при некоторых A, B, C, D, выполниться набор условий:
АВ и ВС и СD и АD?
| № | | | | | № | | | | | № | | | | | |
| 1 | | | | | 11 | | | | | 21 | | | | | |
| 2 | | | | | 12 | | | | | 22 | | | | | |
| 3 | | | | | 13 | | | | | 23 | | | | | |
| 4 | | | | | 14 | | | | | 24 | | | | | |
| 5 | | | | | 15 | | | | | 25 | | | | | |
| 6 | | | | | 16 | | | | | 26 | | | | | |
| 7 | | | | | 17 | | | | | 27 | | | | | |
| 8 | | | | | 18 | | | | | 28 | | | | | |
| 9 | | | | | 19 | | | | | 29 | | | | | |
| 10 | | | | | 20 | | | | | 30 | | | | | |
2. Для универсального множества U={-5,-4,-3,-2,-1, 1, 2, 3, 4, 5}, множества А, заданного списком и для В, являющимся множеством корней уравнения х4+х3+х2+х+=0
а) найти множества АВ, АВ,А\В, В\А, АВ, Ā, С=(АВ)А,
б) выяснить, какая из пяти возможностей выполнена для множеств АиС: АС, или СА, или А=С, или АС=, или А и С находятся в общем положении,
в) найти множество всех подмножеств множества В.
| № | А | | | | | № | А | | | | |
| 1 | -1,1,4,3 | 1 | -12 | -28 | -16 | 16 | -2,1,3,5 | 3 | -7 | -15 | 18 |
| 2 | -1,1,2,3 | 7 | 13 | -3 | -18 | 17 | -3,-1,1,2 | 5 | 1 | -21 | -18 |
| 3 | -1,1,3,4 | -2 | -12 | 18 | 27 | 18 | -2,2,3,4 | 2 | -7 | -20 | -12 |
| 4 | -1,1,2,3 | 0 | -17 | 36 | -20 | 19 | -3,-1,2,4 | -2 | -15 | -4 | 20 |
| 5 | -2,1,3,4 | 0 | -11 | -18 | -8 | 20 | -3,-1,2,3 | -5 | 1 | 21 | -18 |
| 6 | -1,1,4,5 | 3 | -9 | -23 | -12 | 21 | -4,-3,1,2 | 1 | -7 | -13 | -6 |
| 7 | -3,-1,1,2 | -2 | -7 | 20 | -12 | 22 | -5,-1,1,3 | 6 | 0 | -22 | 15 |
| 8 | -4,-1,1,2 | 0 | -11 | 18 | -8 | 23 | -1,1,2,3 | -3 | -3 | 7 | 6 |
| 9 | -1,1,2,3 | -7 | 12 | 4 | -16 | 24 | -1,2,4,5 | 0 | -9 | -4 | 12 |
| 10 | -2,-1,2,4 | -1 | -7 | 13 | -6 | 25 | 1,2,3,4 | 3 | -3 | -7 | 6 |
| 11 | -1,1,2,3 | -4 | 3 | 4 | -4 | 26 | -1,1,2,4 | 1 | -12 | 4 | 16 |
| 12 | -1,1,2,3 | -5 | -3 | 13 | 10 | 27 | -1,1,2,3 | -2 | -4 | 2 | 3 |
| 13 | -3,3,4,5 | -11 | 39 | -49 | 20 | 28 | -3,-2,-1,1 | -4 | -10 | 28 | -15 |
| 14 | 1,2,3,4 | -6 | 8 | 6 | -9 | 29 | -1,2,3,4 | -4 | -2 | 12 | 9 |
| 15 | -2,-1,1,2 | -3 | -2 | 12 | -8 | 30 | -1,2,3,4 | 3 | 1 | -3 | -2 |
3. Пусть A, B, C, - множество точек плоскости, координаты которых удовлетворяют условиям α, β и γ соответственно. Изобразите в системе координат x0y множество D, полученное из множеств A, B и C по формуле δ.
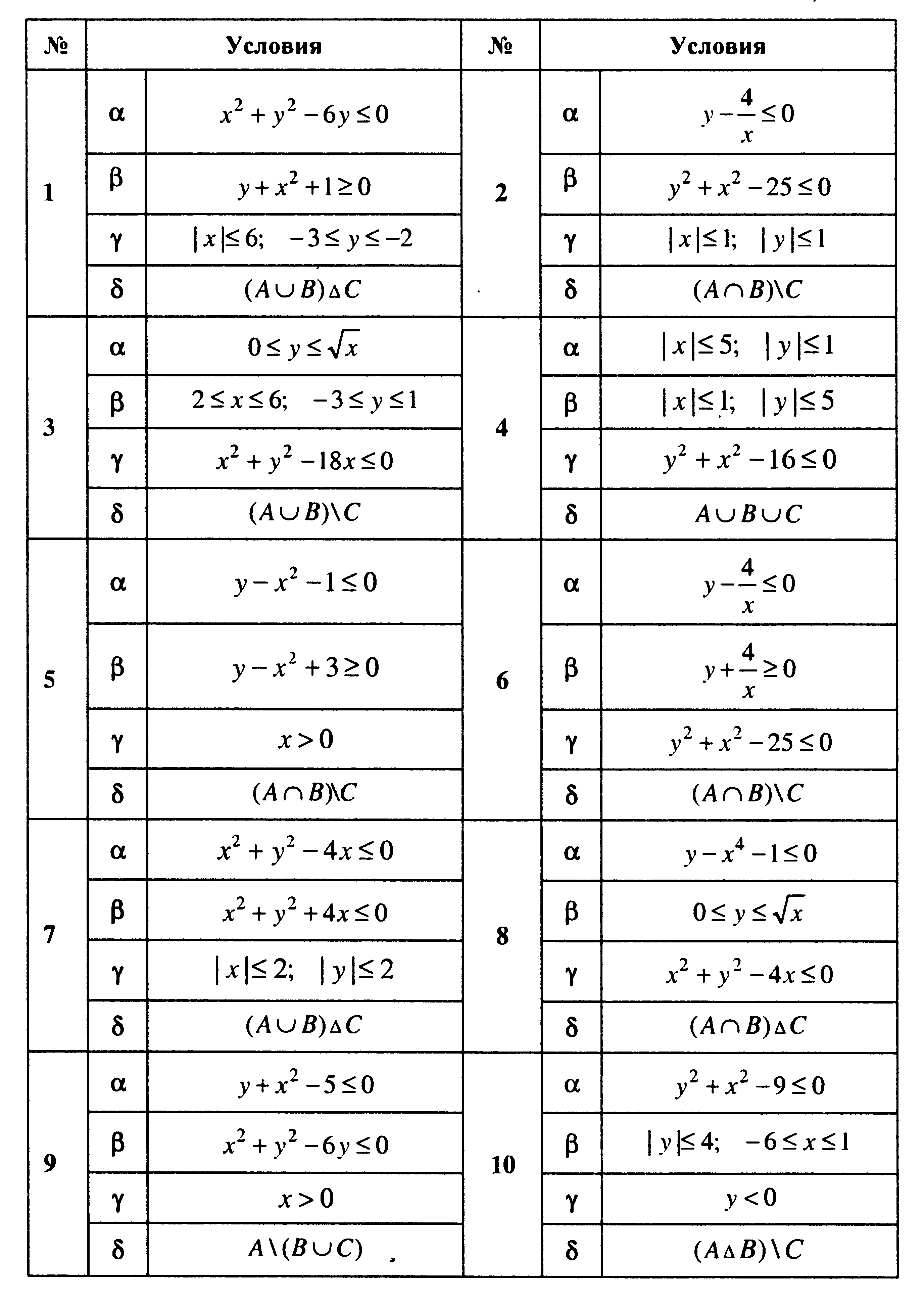

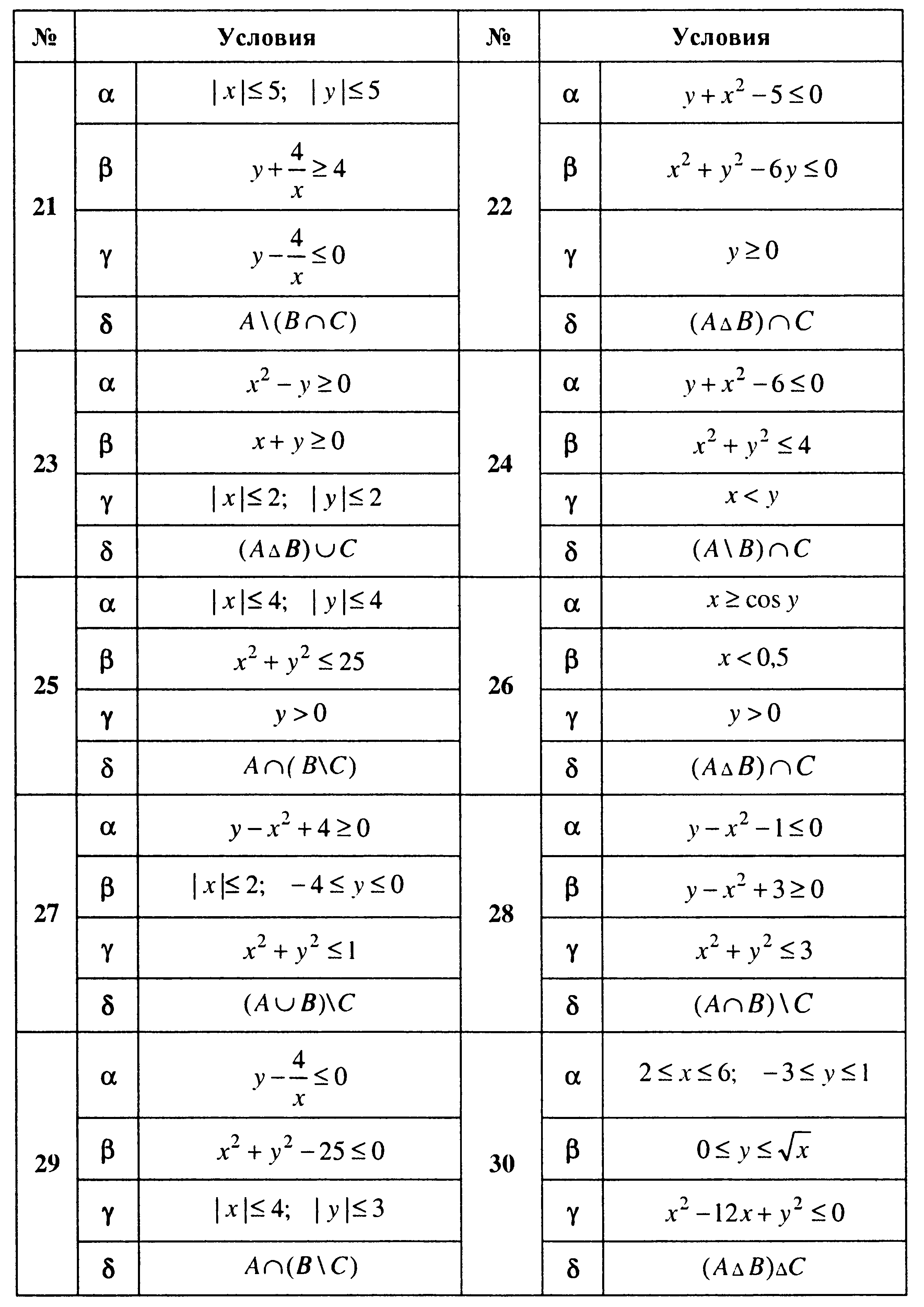
4. Проверить справедливость равенства для А=1,2, В=2,3, С=1,3. Выяснить, верно ли равенство для произвольных А, В, С.
| № | | № | |
| 1 | АС=(А(С\В))(А(СВ)) | 16 | BA=(B(AС)) (BA) |
| 2 | АС=(А(СВ))(АС) | 17 | BA=(BA) (B(A\С)) |
| 3 | А(ВС)=(А(СВ)) \ (А(СВ)) | 18 | B(AС)=(B(A\С)) (BС) |
| 4 | АС=(А(С\В))(АС) | 19 | BA=(BA)(B(AС)) |
| 5 | А(ВС)=(АВ) (А(С\В)) | 20 | B(A\С)=(BA) \ (B(AС)) |
| 6 | А(С\B)=(АС) (А(СВ)) | 21 | BA=(B(AC)) \ (B(C\A)) |
| 7 | АС=(А(СВ)) (АС) | 22 | B(AС)=(BA) \ (B(A\С)) |
| 8 | А(C (ВС))=(А(СВ)) (АС) | 23 | B(A\С)=(BA) (B(AС)) |
| 9 | А(С\B)=(АС) \ (А(СВ)) | 24 | B(A\С)=(BAС)) \ (BС) |
| 10 | А(ВС)=(А(ВС)) (А(СВ)) | 25 | CB=(C(B\A)) (C(BA)) |
| 11 | АС=(А(СВ)) \ (А(B\С)) | 26 | CB=(C(BA)) (CB) |
| 12 | А(ВС)=(АС) \ (А(С\В)) | 27 | C(AB)=(C(AВ)) \ (C(AВ)) |
| 13 | А(ВС)=(А(ВС)) \ (А(ВС)) | 28 | CB=(C(B\A))(CB) |
| 14 | А(С\B)=(А(ВС)) \ (АВ) | 29 | C(AB)=(CA) (C(B\A)) |
| 15 | BA=(B(A\С)) (B(AC)) | 30 | C(B\A)=(CB) (C(AB)) |
5. Для данного графика Р найти: Р-1, Р°Р, Р-1°Р, пр2(Р-1°Р) ´ пр1(Р°Р).
| № | Р | № | Р |
| 1 | (1,2), (1,3), (4,2), (2,3), (3,3) | 16 | (c,c), (c,b), (b,b), (a,b), (c,a) |
| 2 | (2,2), (4,4), (1,2), (3,1), (3,4) | 17 | (e,a), (a,a), (a,e), (e,b), (b,a) |
| 3 | (1,2), (2,3), (3,1), (2,2), (3,2) | 18 | (f,d), (b,d), (d,d), (c,b), (f,c) |
| 4 | (3,3), (3,2), (2,2), (1,2), (3,1) | 19 | (a,a), (a,b), (b,c), (c,a), (c,b) |
| 5 | (0,1), (1,1), (1,0), (0,2), (2,1) | 20 | (a,c), (c,a), (b,b), (a,b), (a,d) |
| 6 | (5,4), (2,4), (4,4), (3,2), (5,3) | 21 | (c,g), (g,d), (d,d), (g,c), (d,c) |
| 7 | (1,1), (1,2), (2,3), (3,1), (3,2) | 22 | (e,b), (b,c), (c,c), (c,e), (e,e) |
| 8 | (3,1), (1,3), (2,2), (1,2), (1,4) | 23 | (a,f), (f,b), (b,b), (a,a), (a,c) |
| 9 | (3,8), (8,4), (4,4), (8,3), (4,3) | 24 | (e,b), (e,c), (e,e), (a,b), (b,c) |
| 10 | (0,2), (2,3), (3,0), (3,3), (0,0) | 25 | (x,y), (x,z), (t,y), (z,z), (y,z) |
| 11 | (1,5), (5,2), (2,2), (1,1), (1,3) | 26 | (y,y), (t,t), (x,y), (z,x), (z,t) |
| 12 | (0,2), (0,3), (0,0), (1,2), (2,3) | 27 | (x,y), (y,z), (z,x), (y,y), (z,y) |
| 13 | (а,b), (a,c), (d,b), (c,c), (b,c) | 28 | (z,z), (z,y), (y,y), (x,y), (z,x) |
| 14 | (b,b), (d,d), (a,b), (c,a), (c,d) | 29 | (t,x), (x,x), (x,t), (t,y), (y,x) |
| 15 | (a,b), (b,c), (c,a), (b,b), (c,b) | 30 | (w,t), (y,t), (t,t), (z,y), (w,z) |
6. Выяснить, какими из свойств обладает данное отношение F=(A, G). Выяснить, что представляет собой отношение F°F, F°F-1. Построить на конечном множестве отношение, обладающее таким же набором свойств, что и данное. Построить на бесконечном множестве отношение, обладающее набором свойств, противоположным данному. В случае невозможности построения доказать противоречивость набора требований.
| № | A | G |
| 1 | Множество студентов РГГУ | xryÛx и y учатся на одном курсе |
| 2 | P(U), гдеU – множество точек плоскости | А r В Û А Ç В =Æ |
| 3 | Множество окружностей на плоскости | xryÛx касается y |
| 4 | Жители Тольятти на начало этого года | xryÛx и yсупруги |
| 5 | Жители России на начало этого года | xryÛx и yсостоят в одной и той же политической партии |
| 6 | Прямые в пространстве | xryÛx и yимеют хотя бы одну общую точку |
| 7 | Жители Тольятти на начало этого года | xryÛx и yразного возраста |
| 8 | N | xryÛx и yимеют одинаковый остаток от деления на 3 |
| 9 | P(N) | А r В Û½А½=½В½ |
| 10 | R | x r y Û 2x > y2 |
| 11 | {(a1, a2,…, an): aiÎ{0,1}} | xryÛx и yотличаются только в одной координате |
| 12 | R2 | (x, y) r (z, t) Û x=z и y=t |
| 13 | R | x r y Û x2 + y2=1 |
| 14 | Жители России на начало этого года | xryÛx старше y |
| 15 | [0, 4] | x r y Û x >2y+1 |
| 16 | R | xryÛx и y имеют одинаковую целую часть |
| 17 | N | xryÛxy кратно трем |
| 18 | P(U), гдеU – множество точек плоскости | А r В Û А и В – в общем положении |
| 19 | Жители Тольятти на начало этого года | xryÛy – теща для х |
| 20 | [0, 2] | x r y Û x + y<1 |
| 21 | N2 | (x, y) r (z, t) Ûxz = yt |
| 22 | N | xryÛx +y кратно трем |
| 23 | Непрерывные на [0, 1] функции | |
| 24 | Rn | (a1, …, an) r (b1,…, bn) Û {max ai, 1£i£n}={max bi, 1£i£n} |
| 25 | Жители Тольятти на начало этого года | xryÛx - отец для y |
| 26 | R | x r y Û x =2y+3 |
| 27 | Читатели библиотеки РГГУ | xryÛx и yпрочитали одну и ту же книгу |
| 28 | P(U), гдеU – множество точек плоскости | А r В Û А Ç В =Æ |
| 29 | Векторы на плоскости | xry Û½x½=½y½ |
| 30 | Жители России на начало этого года | x r y Û x внук y |