Файл: Индивидуальное домашнее задание по дискретной математике.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 335
Скачиваний: 21
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
18. Найдите степени всех вершин, радиус и диаметр графа G. Найдите хроматическое число графа, проведя его раскраску по методу минимальной раскраски. Является ли изображенный граф планарным?
| № | G | № | G |
| 1 | 1 2 3 4  5 6 7 8 | 16 | 1 2 3 4  5 6 7 8 |
| 2 | 1 2 3 4  5 6 7 8 | 17 | 1 2 3 4    5 6 7 8 |
| 3 | 1 2 3 4  5 6 7 8 | 18 | 1 2 3 4  5 6 7 8 |
| 4 | 1 2 3 4  5 6 7 8 | 19 | 1 2 3 4  5 6 7 8 |
| 5 | 1 2 3 4  5 6 7 8 | 20 | 1 2 3 4  5 6 7 8 |
| 6 | 1 2 3 4  5 6 7 8 | 21 | 1 2 3 4  5 6 7 8 |
| 7 | 1 2 3 4  5 6 7 8 | 22 | 1 2 3 4 5 6 7 8 |
| 8 | 1 2 3 4  5 6 7 8 | 23 | 1 2 3 4  5 6 7 8 |
| 9 | 1 2 3 4  5 6 7 8 | 24 | 1 2 3 4  5 6 7 8 |
| 10 | 1 2 3 4  5 6 7 8 | 25 | 1 2 3 4  5 6 7 8 |
| 11 | 1 2 3 4 5 6 7 8 | 26 | 1 2 3 4  5 6 7 8 |
| 12 | 1 2 3 4  5 6 7 8 | 27 | 1 2 3 4  5 6 7 8 |
| 13 | 1 2 3 4  5 6 7 8 | 28 | 1 2 3 4  5 6 7 8 |
| 14 | 1 2 3 4  5 6 7 8 | 29 | 1 2 3 4  5 6 7 8 |
| 15 | 1 2 3 4  5 6 7 8 | 30 | 1 2 3 4  5 6 7 8 |
19.Составив таблицы истинности, выясните, равносильны ли следующие формулы алгебры высказываний: F(X,Y,Z) и G(X,Y,Z).
| № | F(X,Y,Z) | G(X,Y,Z) | | ||
| 1 |  [ [ X↔((Y X↔((Y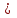  Z)→ Z)→ (X (X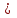  Y))] Y))] | ((  X X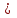  Z) Z)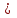 (X (X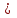 Z)) Z))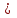  Y Y | |||
| 2 | ((X→Y)Z) ((XY)↔Z) | (XYZ)((X→Y)Z) | |||
| 3 | (  (X (X (Y (Y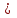  Z)) Z))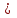  X) X)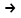 ( ( (X (X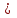  Y) Y)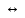 Z) Z) | X 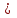 (Y (Y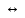 Z) Z) | |||
| 4 | ((X^(YZ)) ¬(X ¬ Z)) ¬ (¬YZ) | ¬(XZ) Y | |||
| 5 | ¬ [((¬Y۷ ¬Z)↔X)۸(¬X۸(Y→ ¬Z))] | (X۸Y۸Z) ۷ ¬X۷ (X۸ ¬Y) ۷ (X۸Y۸ ¬Z) | |||
| 6 | 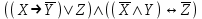 | 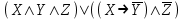 | |||
| 7 | 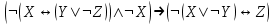 | 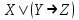 | |||
| 8 | 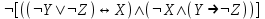 | 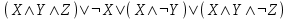 | |||
| 9 | 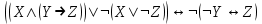 | 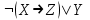 | |||
| 10 | ┐[ ┐ X ↔ ((YV┐Z) → ┐(XV ┐Y))] | ((┐X ┐Z) V (X Z)) ┐Y | |||
| 11 | 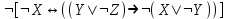 | 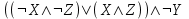 | |||
| 12 | (  (X↔(Y (X↔(Y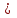  Z)) Z))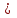  X)→( (X X)→( (X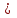  Y)↔Z) Y)↔Z) | X 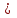 (Y↔ Z) (Y↔ Z) | |||
| 13 | = ((X٨(Y→Z)) ٧¬(X٧¬Z)↔( ¬Y↔Z) | ¬(X→Z) ٧Y | |||
| 14 |  [ [  X↔((Y X↔((Y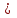  Z) → Z) →  (X (X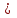  Y)) ] Y)) ] | ((  X X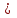  Z) Z)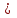 (X (X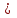 Z)) Z))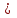  Y Y | |||
| 15 | ((X→Y)Z) ((XY)↔Z) | (XYZ)((X→Y)Z) | |||
20. Построить таблицу данной булевой функции f(x, y, z)
| | f(x, y, z) | № | f(x, y, z) | № | f(x, y, z) |
| 1 | x + y z → 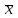 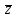 | 11 | x y 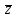 → x y → x y | 21 | (x → y) + z 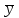 |
| 2 | (x│y) → 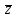 y + z y + z | 12 | (x + y) + (z 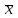 ) ) | 22 | (x y) z + y |
| 3 | (x → 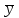 ) + z x ) + z x | 13 | x y + z→ 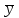 | 23 | (x y) + z → y |
| 4 | x y + 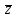 y y | 14 | (x y) + z 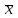 | 24 | x y + z → 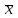 |
| 5 | x 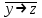 + y + y | 15 | (x y → 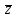 ) + y ) + y | 25 | (x + (y z)) + y |
| 6 | 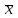 y → z y y → z y | 16 | x y + z 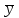 | 26 | 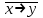 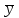 + z + z |
| 7 | (x y) 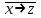 | 17 | x y 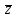 + y + y | 27 | (x│y) + (y → z 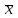 ) ) |
| 8 | (x y → z) x+y | 18 | (x → 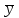 ) + (z y) ) + (z y) | 28 | 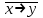 (x (x 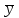 + z) + z) |
| 9 | (x│y) → 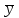 x x | 19 | (x + y) z 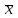 | 29 | y + z z x x |
| 10 | (x → y z) + 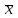 | 20 | (x│y) z 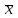 | 30 | x 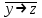 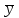 + z + z |
21. Написать таблицу функции h(x,y), являющуюся суперпозицией функций fnи fk, если f1=(1001 0111), f2=(0110 1011), f3=(1110 0110), f4=(0111 0011), f5=(1100 0111), f6=(1001 0100), f7=(1011 0101), f8=(1000 0110), f9=(1010 0110), f10=(0101 1000).
| № | n | k | h(x,y) | № | n | k | h(x,y) | № | n | k | h(x,y) |
| 1 | 1 | 2 | fn(x, fk(x,x,y),y) | 11 | 4 | 3 | fn(x,y, fk(y,x,y)) | 21 | 10 | 5 | fn(fk(x,y,y),x,y) |
| 2 | 2 | 2 | fn(x, fk(y,x,y),x) | 12 | 2 | 4 | fn(x,fk(x,y,y),y) | 22 | 7 | 9 | fn(fk(y,y,x),x,y) |
| 3 | 1 | 1 | fn(y, fk(x,y,x),x) | 13 | 5 | 7 | fn(x,y, fk(y,x,x)) | 23 | 8 | 7 | fn(fk(x,y,y),y,x) |
| 4 | 3 | 5 | fn(x, fk(y,x,y),y) | 14 | 9 | 8 | fn(y,y, fk(x,y,x)) | 24 | 7 | 8 | fn(fk(x,y,x),x,y) |
| 5 | 3 | 2 | fn(y, fk(x,y,x),x) | 15 | 7 | 5 | fn(x,y, fk(x,y,y)) | 25 | 6 | 7 | fn(fk(y,x,x),y,x) |
| 6 | 4 | 3 | fn(x, fk(y,y,x),y) | 16 | 8 | 7 | fn(x,x, fk(y,x,y)) | 26 | 9 | 2 | fn(x, fk(y,y,x),y) |
| 7 | 2 | 3 | fn(x,fk(x,y,y),y) | 17 | 7 | 8 | fn(y, fk(x,y,x),y) | 27 | 2 | 10 | fn(x,y, fk(x,y,x)) |
| 8 | 5 | 2 | fn(y,x, fk(x,x,y)) | 18 | 5 | 9 | fn(x, fk(y,x,x),y) | 28 | 3 | 9 | fn(fk(y,y,x),x,x) |
| 9 | 5 | 4 | fn(fk(x,y,y),x,y) | 19 | 5 | 10 | fn(y, fk(x,y,x),x) | 29 | 10 | 7 | fn(y,x, fk(x,y,x)) |
| 10 | 3 | 2 | fn(x,x, fk(x,y,y) | 20 | 10 | 9 | fn(x, fk(x,x,y),y) | 30 | 8 | 3 | fn(x, fk(y,y,x),y) |
22. По функциям f и g, заданным векторно, построить векторное представление функции h:
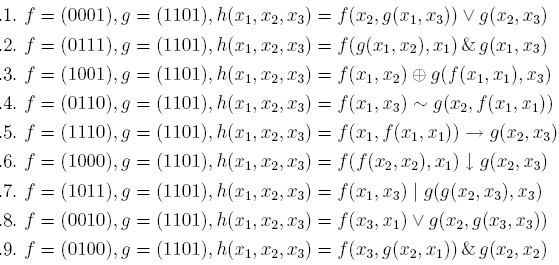
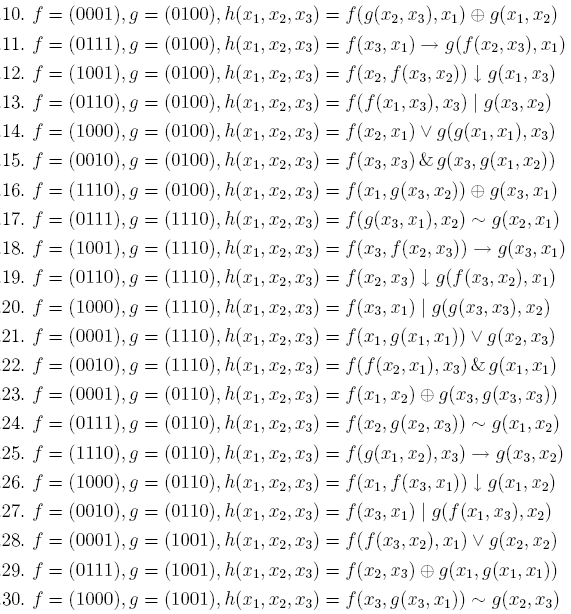
23. Для данной функции f(x,y,z) выяснить какие ее переменные являются фиктивными, а какие существенными. Выразить f(x,y,z) формулой, содержащей только существенные переменные.
| № | f(x,y,z) | № | f(x,y,z) | № | f(x,y,z) | № | f(x,y,z) | № | f(x,y,z) |
| 1 | 1011 1011 | 7 | 0010 0010 | 13 | 0100 0100 | 19 | 1111 0101 | 25 | 0110 0110 |
| 2 | 0011 1100 | 8 | 1100 0011 | 14 | 1111 0011 | 20 | 0111 0111 | 26 | 1010 1111 |
| 3 | 0101 1111 | 9 | 0000 1010 | 15 | 0000 0101 | 21 | 1010 0101 | 27 | 1010 1010 |
| 4 | 1000 1000 | 10 | 1001 1001 | 16 | 0000 0011 | 22 | 0011 0011 | 28 | 1110 1110 |
| 5 | 1010 0000 | 11 | 0101 0000 | 17 | 0011 0000 | 23 | 1011 1011 | 29 | 0001 0001 |
| 6 | 1100 1111 | 12 | 1100 1100 | 18 | 1101 1101 | 24 | 1111 1100 | 30 | 0011 1111 |