Файл: Индивидуальное домашнее задание по дискретной математике.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 04.12.2023

Просмотров: 334

Скачиваний: 21

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.


12. Из данной пропорции найти х и y


№

пропорция
№
пропорция

1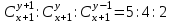


16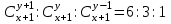


2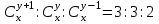


17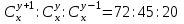


3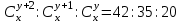


18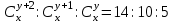


4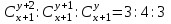


19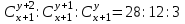


5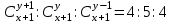


20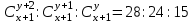


6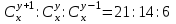


21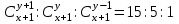


7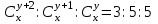


22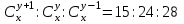


8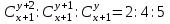


23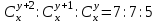


9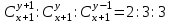


24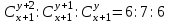


10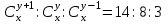


25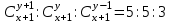


11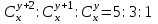


26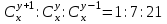


12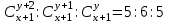


27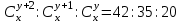


13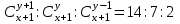


28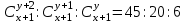


14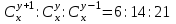


29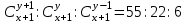


15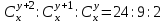


30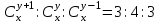



13. Найти коэффициенты при xk в разложении данного выражения Р по полиномиальной формуле, полученный после раскрытия скобок и приведения подобных членов.


№
k
P
№
k
P
№
k
P

1
23
(2+x2-x3)13
11
112
(4+x18+x4)28
21
44
(2+x10-x4)11

2
96
(1+x6-x10)17
12
46
(1-x4+x6)14
22
27
(3+x3+x9)9

3
80
(4-x8+x6)14
13
48
(3+x5-x3)16
23
56
(2-x2+x9)29

4
130
(x7-2+x5)26
14
40
(3+x3-x4)13
24
68
(1+x10-x4)18

5
66
(x7+3-x3)22
15
132
(2-x6+x14)23
25
60
(2-x4+x7)16

6
48
(1+x7-x2)25
16
34
(4+x2-x5)17
26
17
(7-x+x4)14

7
114
(3+x14+x6)20
17
96
(1+x4-x14)24
27
150
(2-x5-x7)32

8
30
(x7+3-x2)16
18
57
(2-x3+x7)19
28
120
(x14-3+x8)15

9
18
(2+x6-x2)9
19
60
(1+x14-x4)15
29
34
(x2+2-x8)15

10
22
(3-x2+x5)12
20
9
(5-x-x3)10
30
300
(x10-3+x14)31


14. Сколько натуральных чисел от 1до 10000 не делится ни на, ни на , ни на , ни на ?


№








№








№








1
4
5
6
7
11
11
8
5
4
21
2
5
4
13

2
2
3
4
5
12
7
9
5
3
22
2
8
5
3

3
3
4
5
8
13
3
8
16
7
23
11
7
9
3

4
6
7
3
2
14
13
9
5
3
24
3
6
5
4

5
5
8
9
4
15
3
5
6
7
25
4
8
19
3

6
3
4
5
6
16
11
8
3
2
26
19
5
10
2

7
2
4
5
7
17
17
2
3
4
27
5
6
7
8

8
3
6
7
11
18
2
5
4
17
28
11
3
9
5

9
11
3
9
10
19
3
4
6
17
29
12
3
5
19

10
7
9
5
3
20
13
2
3
4
30
23
2
8
7


15. Дана реализация графов. Определить к какому типу относятся графы. Задать графы списками вершин и ребер и с помощью матриц смежности и инцидентности. Определить степени всех вершин в графе G, полустепени исхода и полустепени захода всех вершин в орграфе D.

№
G
D

1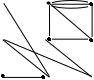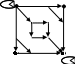







2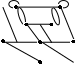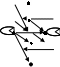






3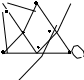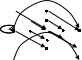






4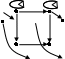






5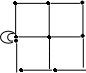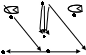








6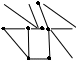






7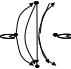






8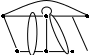






9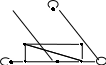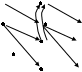






10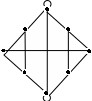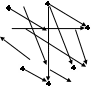







16. С помощью матрицы смежности определить количество путей длины 2,3,4 из V1 в V4, из V2 в V5, определить для всех вершин графа полустепени исхода и захода, выяснить имеются ли контуры в графе. Построить реализации графов.
1 . 2. 3. 4.

5 . 6. 7. 8.

9. 10.

17. Даны графы G1 и G2 . Найдите G1ÈG2, G1∩ G2, G1ÅG2 аналитически и изобразить результат графически. Для графа G1ÈG2 найдите матрицу смежности, матрицу инцидентности, компоненты сильной связности, маршруты (но не цепи) длины 7; простые цепи, простые циклы, исходящие из вершины 1.


№
G1
G2
№
G1
G2

1
1 2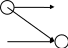



4 3
1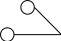



3 2
16
1 2



4 3
1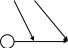



3 2

2
1 2



4 3
1

3 2
17
1 2



4 3
1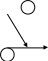



3 2

3
1 2



4 3
1



3 2
18
1 2



4 3

1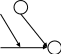



3 2

4
1 2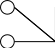



4 3
1



3 2
19
1 2



4 3
1



3 2

5
1 2



4 3
1



3 2
20
1 2



4 3
1



3 2

6
1 2



4 3

1

3 2

21
1 2



4 3
1



3 2

7
1 2



4 3
1



3 2
22
1 2



4 3
1



3 2

8
1 2



4 3
1



3 2
23
1 2



4 3
1



3 2

9
1 2



4 3
1



3 2
24
1 2



4 3
1



3 2

10
1 2



3 4
1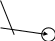



3 2
25
1 2



4 3
1



3 2

11
1 2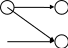



4 3
1



3 2
26
1 2



4 3
1



3 2

12
1 2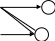



4 3
1



3 2
27
1 2



4 3
1



3 2

13
1 2



4 3
1



3 2
28
1 2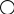



4 3
1



3 2

14
1 2



4 3
1



3 2
29
1 2



4 3
1



3 2

15
1 2



4 3

1



3 2

30
1 2



4 3
1



3 2

Смотрите также файлы