7. Дано соответствие Г=(X, Y, G). Выяснить, какими из 4 основных свойств (всюду определенность, сюръективность, функциональность, инъективность) обладает Г. Найти образ множества А и прообраз множества В при данном соответствии. Построить соответствие между бесконечными множествами, обладающее тем же набором свойств, что и Г. Построить соответствие между конечными множествами, обладающее набором свойств, противоположным данному.

№	X	Y	G	A	B
1	a, b, c, d, e	1, 2, 3	(a,2), (b,3), (c,1), (d,2), (e,1)	e,c	2,3
2	a, b, c, d	1, 2, 3, 4	(a,4), (b,3), (c,2), (d,1)	a,b	1,3
3	a, b, c, d	1, 2, 3, 4, 5	(a,3), (b,5), (c,4), (d,1)	a,c	1,4
4	a, b, c, d, e	1, 2, 3, 4	(d,1), (b,2), (e,4), (a,3)	b,c	1,2
5	a, b, c, d, e	1, 2, 3	(b,2), (c,1), (e,3), (a,3)	e,c	3,1
6	a, b, c, d	1, 2, 3, 4	(a,2), (b,3), (c,1), (a,4)	a,b	1,2
7	a, b, c, d, e	1, 2, 3, 4, 5	(a,5), (b,3), (d,1), (e,2)	d,e	1,3
8	a, b, c, d	1, 2, 3, 4	(a,3), (b,4), (c,3), (d,1)	a,c	1,3
9	a, b, c	1, 2, 3, 4, 5	(a,2), (b,1), (c,5), (a,3)	a,b	3,4
10	a, b, c	1, 2, 3	(a,1), (a,3), (b,2), (c,3)	a,c	2,3
11	a, b, c, d	1, 2, 3, 4, 5	(a,2), (c,1), (d,5), (c,3)	b,c	1,2
12	a, b, c, d, e	1, 2, 3, 4	(b,1), (c,3), (d,2), (c,1)	a,c	1,2
13	a, b, c, d	1, 2, 3	(a,1), (b,1), (c,3), (b,2)	b,d	1,3
14	a, b, c, d	1, 2, 3, 4	(a,4), (b,3), (b,2), (c,3), (d,4)	a,b	3,4
15	a, b, c, d	1, 2, 3, 4	(a,4), (c,4), (b,2) (a,3)	a,b	2,4
16	a, b, c, d, e	1, 2, 3	(a,2), (b,1), (d,3), (e,1)	a,b	1,2
17	a, b, c, d	1, 2, 3, 4	(b,3), (a,2), (c,2), (d,1)	a,c	1,4
18	a, b, c, d	1, 2, 3, 4	(a,3), (c,2), (d,1), (c,4)	c,d	2,3
19	a, b, c	1, 2, 3, 4, 5	(a,2), (b,5), (c,4), (b,3)	a,b	2,5
20	a, b, c, d	1, 2, 3	(a,1), (b,3), (a,2), (c,4)	a,b	2,3
21	a, b, c, d	1, 2, 3	(a,3), (b,3), (c,1), (d,2)	c,d	1,3
22	a, b, c, d	1, 2, 3	(a,1), (b,3), (c,2), (a,2)	c,d	2,3
23	a, b, c, d	1, 2, 3, 4	(a,3), (b,4), (c,1), (d,2)	a,b	1,4
24	a, b, c	1, 2, 3, 4	(a,3), (b,1), (c,2), (c,1)	a,c	4,2
25	a, b, c, d, e	1, 2, 3	(c,2), (d,1), (a,3), (b,3)	a,d	3,1
26	a, b, c, d	1, 2, 3, 4	(b,2), (c,3), (d,1), (b,4)	b,c	1,2
27	a, b, c, d, e	1, 2, 3, 4, 5	(b,5), (c,3), (e,1), (a,2)	a,e	1,3
28	a, b, c, d	1, 2, 3, 4	(b,3), (c,4), (d,3), (a,1)	b,d	3,1
29	a, b, c	1, 2, 3, 4, 5	(b,2), (c,1), (a,5), (b,3)	b,c	4,3
30	a, b, c	1, 2, 3	(b,1), (b,3), (c,2), (a,3)	a,b	2,3

---

8. Дано соответствие Г=(X, Y, G). Выяснить, какими из 4 основных свойств (всюду определенность, сюръективность, функциональность, инъективность) обладает Г. Построить соответствие между конечными множествами, обладающее набором свойств, противоположным данному.

№	Х	Y	G
1	Многочлены 2 степени от одной переменной с действительными коэффициентами	R	(многочлен, его корень)
2	Множество кругов на плоскости	Множество точек плоскости	(круг, его центр)
3	(0, +)	[-1, 1]	(x, y): x2
4	N={1, 2, …}	R	(x, lnx)
5	R	Непрерывные на [a, b] функции	(max f(x), f(x)) x[a, b]
6	Вузы г. Тольятти	Жители г. Тольятти	(вуз; человек, окончивший этот вуз)
7	(0, +)	Отрезки на прямой	(х, отрезок длины х)
8	Фамилии студентов вашей группы	{1, 2, …, 100}	(фамилия, число букв в фамилии)
9	Окружности на плоскости	Z	(окружность, ее длина)
10	Функции, определенные на [0, 1]	R	(функция, ордината ее точки максимума)
11	R2	N	((x, y), )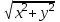
12	Имена студентов вашей группы	Буквы русского алфавита	(имя, буква из имени)
13	N	Студенты нашего вуза	(n, человек с годом рождения n)
14	[0, 1]	{0, 1}	(x, f(x)) 0, xR\Q f(x)= 1, xQ
1 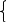5	R	R10	(max ai, (a1, a2,…,a10)) 1i10
16	Окружности на плоскости	Прямые на плоскости	(окружность, касательная к окружности)
17	[(P(U)]3	P(U)	((A, B, C), ABC)
18	[0, 1]	R2	(x, (x,y): x2+y2=1)
19	R	Функции непре-рывные на [0, 1]	(m, f(x): min f(x)=m) 0x1
20	{0, 1, 2}	N	(x,y): х – остаток от деления y на 3
21	[1, 3]	R+	(x,y): (x-2)2+(y-2)21
22	Пары окружностей на плоскости	R2	(пара окружностей, координаты точки пересечения этих окружностей)
23	Множество книг в библиотеке РГГУ	Z	(книга, число страниц в этой книге)
24	(-4, 4)	[1, 6]	(x,y): y=x-2+1
25	Мужчины г. Тольятти	Женщины г. Тольятти	(x,y): x и y состоят или когда-либо состояли друг с другом в законном браке
26	[(P(U)]2	P(U)	((A, B), A\B)
27	Политические партии г. Тольятти	Жители г. Тольятти	(партия, человек, состоящий в этой партии)
28	P(U)	[(P(U)]2	(D, (A, B, C,): ABC=D)
29	P(U), где U={1, 2, …, 40}	N	(A, A), где АP(U)
30	Пары прямых на плоскости	R	(пара прямых, абсцисса точки пересечения прямых)

---

9. Сколькими способами из колоды в 36 листов можно выбрать не упорядоченный набор из 5 карт так, чтобы в этом наборе было бы точно:

№	Условие
1	1 король, 2 дамы, 1 пиковая карта
2	1 крестовая карта, 2 дамы, нет червей
3	Хотя бы 4 крестовые карты, 1 туз
4	3 дамы, 2 крестовые карты
5	1 бубновая карта, 2 крестовых, 1 дама
6	2 бубновые, 2 крестовые карты, 1 туз
7	По крайней мере 4 пиковые карты, 1 дама
8	карты черной масти , 2 дамы
9	1 туз, 1 валет, 1 карта красной масти
10	3 туза, 3 карты черной масти
11	1 дама, 1 карта пик, 2 крестовые карты
12	2 дамы, 2 туза, 1 карта пиковой масти
13	дама и король одной масти, 1 пиковая карта
14	1 король, 2 дамы, 1 карта красной масти
15	Не меньше 4 красных карт, 2 туза
16	2 черных карты, 1 карта червей, 1 туз
17	3 короля, 2 бубновых карты
18	1 король, 1 дама, 1 крестовая карта
19	2 крестовых карты, 1 бубновая, 1 дама
20	1 бубновая карта, 2 дамы, нет червей
21	3 бубновых карты, 2 дамы, 1 валет
22	2 туза, не меньше 3 пиковых карт
23	2 карты красной масти, 3 туза
24	2 дамы, 1 бубновая карта, 1 пиковая карта
25	1 валет, нет дам, 3 черные карты
26	2 туза, по крайней мере 4 красные карты
27	Валет и дама черной масти, не более 1 туза
28	1 туз, 3 дамы, не больше 2 карт красной масти
29	2 крестовые карты, хотя бы 2 туза
30	2 дамы, 1 король, нет червей

---

10. Сколько различных слов можно получить перестановкой букв слова ?

№		условие
1	Атаман	Согласные идут в алфавитном порядке, но буквы «а» не стоят рядом
2	Ворон	Две буквы «о» не стоят рядом
3	Интернирование	Согласные и гласные чередуются, гласные идут в алфавитном порядке
4	Взбрыкнул	Между двумя гласными находятся 3 согласные
5	Пастух	Между двумя гласными находятся 2 согласные
6	Околоток	Ровно 3 буквы «о» не идут подряд
7	Криминал	Пятое и седьмое места заняты согласными
8	Переходим	Согласные и гласные чередуются
9	Перешеек	Четыре буквы «е» не идут подряд
10	Диктатура	Как гласные, так и согласные идут в алфавитном порядке
11	Катастрофа	Не меняется порядок согласных букв
12	Танкетка	Запрещено буквосочетание «ант»
13	Комитет	Гласные не стоят рядом и разделяются буквами «т»
14	Парламент	Согласные идут в алфавитном порядке, гласные – порядке, обратном алфавитному
15	Диссидент	Гласные чередуются с парами согласных
16	Полумера	Не встречается буквосочетание «мурло»
17	Министр	Нельзя сказать, что согласные идут в алфавитном порядке
18	Передел	В начале и в конце слова стоит согласная буква
19	Приватизация	Чередуются пары гласных и согласных букв
20	Салага	Буква «а» идет непосредственно после «с»
21	Президент	Согласные идут в алфавитном порядке
22	Кишмиш	Одинаковые буквы не идут друг за другом
23	Полномочия	Никакие гласные не стоят рядом
24	Логарифм	Второе, четвертое и шестое места заняты согласными
25	Ультиматум	Между буквами «т» стоят все гласные и только они
26	Переворот	Не больше одной пары одинаковых букв стоят рядом
27	Капитуляция	Слово начинается с буквы «а», чередуются гласные и согласные буквы
28	Легитимность	Не присутствуют буквосочетания «гимн» и «тост»
29	Белиберда	Между буквами «б» стоит блок из четырех гласных
30	Коммунизм	Не встречается сочетание букв «муки»

---

11. Найти наибольший член разложения бинома (a+b)ⁿ

№	a	b	n	№	a	b	n	№	a	b	n
1		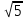3	17	11		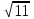3	13	21		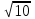2,8	15
2		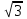10	17	12	4		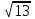10	22	2,8		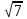19
3		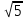2	13	13		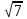2,5	21	23		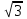1,9	18
4	3		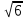12	14	3		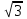18	24	2,8		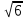17
5		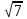3	15	15		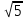3	10	25		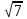2,5	16
6	3		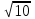19	16	2,2		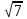13	26	2,3		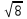20
7		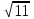4	14	17		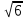2,5	11	27		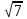2,7	18
8	3		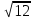13	18	3,5		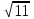10	28	3,5		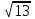15
9		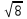3	12	19		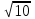3,3	13	29		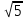2,3	17
10	4	2	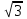11	20	3,2		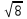9	30	3,2		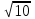20

---

Смотрите также файлы

• Тема Основы языка Python.pdf

• Педагогу необходимо научиться строить общение с ребенком на основе уважения и взаимной любви, развивать доверие и эмпатию, учитывать индивидуальные потребности и особенности каждого ребенка.docx

• Оптимизация бизнеспроцессов.docx

• В аптечной организации.docx

• Уроков победителей конкурса "Учитель года" "Как создать электронную презентацию".docx