ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 90
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
= b2/b1.
Пример 2. Для путешествия был заготовлен запас продовольствия для 45 человек на 96 дней. На сколько дней хватит этот же запас продовольствия для 30 человек ?
▼ Составим схему по условию задачи:
Зависимость обратно пропорциональная, так как если увеличить количество человек, то этот же запас продовольствия хватит на меньшее число дней. Условно обозначим такую зависимость разно направленными стрелками.
Запишем пропорцию:
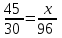
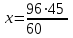= 144 дня.
Ответ. 144 дня.▲
Задание 1. За 3,2 кг товара заплатили 11,52 р. Сколько следует заплатить за 1,5 кг этого товара?
▼ Составим схему по условию задачи:
Зависимость между количеством товара и стоимостью покупки прямо пропорциональная, так как если купить товара в несколько раз больше, то и стоимость покупки увеличится во столько же раз. Условно обозначим такую зависи
Пример. Только 94% из 27 500 выпускников города правильно решили задачу B1. Сколько человек правильно решили задачу В1?
▼ Правильно решили задачу 27 500·0,94 = 25 850 учеников.▲
II. Нахождение числа по его процентам. Если известно, что a% числа х равно b, то число х находится по формуле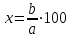
. Например, если известно, что 12% числа равно 30, то искомое число 
.
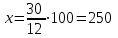Пример. В школе французский язык изучают 124 учащихся, что составляет 25% от числа всех учащихся школы. Сколько учащихся в школе?
▼ Пусть х – число учащихся школы, тогда искомое число есть
▲
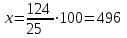Пример. Студентами технических вузов собираются стать 27 выпускников школы. Они составляют 30% от числа выпускников. Сколько в школе выпускников?
▼ Пусть х – число выпускников школы, тогда искомое число есть
▲
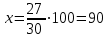III. Нахождение процентного отношения чисел. Чтобы найти процентное отношение двух чисел aи b, надо отношение этих чисел умножить на 100%, т.е. вычислить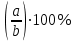
. Например, сколько процентов составляет 120 от 60: ▼
▲
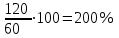В задачах часто говорится об изменении какой-либо величины на определенный процент. Что это значит?
Повышение цены на 10% означает, что к прежней цене х прибавили 0,1х, т.е. новая цена составит х + 0,1х = 1,1х.
Скидка на 25% означает, что прежняя цена х уменьшилась на 25%, т.е. новая цена составит х - 0,25х = 0,75х.
Правило: За 100% принимаем ту величину, с которой сравниваем.
Справедливы следующие утверждения:
• если величину хувеличить на p%, то получим х(1 + 0,01p);
• если величину хуменьшить на q%, то получим х(1 - 0,01q);
• если величину хувеличить на p%, а полученный результат уменьшить на q %, то получим
x(1 + 0,01p)(1 - 0,01q);
• если величину хдваждыувеличить на p%, то получим х(1+ 0,01p)2;
• если величину хдважды уменьшить на q%, то получим х(1- 0,01q)2;
• положенная в банк под p% годовых начальная сумма S0 через n лет с учетом процентов достигнет величины Sn = S0 (1 + 0,01p)n.
Задание 1. Учитель зарабатывает на 25% меньше, чем профессор. На сколько процентов больше, чем учитель, зарабатывает профессор?
▼ Если х - зарплата профессора, то х – 0,25х = 0,75х - зарплата учителя.
Профессор зарабатывает больше, чем учитель на 0,25х, или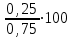
= 33,3%.▲
Задание 2. Цена на электрический чайник была повышена на 16% и составила 3480 рублей. Сколько рублей стоил чайник до повышения цены?
▼ Пусть х – первоначальная цена чайника. Составляем уравнение:
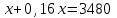, или 
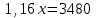
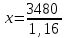= 3000 руб.
Таким образом, цена чайника до повышения составляла 3000 рублей.
Ответ: 3000.▲
Задание 3. Пачка сливочного масла стоит 60 рублей. Пенсионерам магазин делает скидку 5%. Сколько рублей стоит пачка масла для пенсионера?
▼ Пачка сливочного масла для пенсионеров: 60·(1 - 0,05) = 57 руб.▲
Задание 4. Тетрадь стоит 24 рубля. Сколько рублей заплатит покупатель за 60 тетрадей, если при покупке больше 50 тетрадей магазин делает скидку 10% от стоимости всей покупки?
▼ Покупатель заплатит за 60 тетрадей со скидкой: 60·24∙(1 - 0,1) = 1296 руб.▲
Задание 5. В связи с распродажей диван подешевел на 20% и теперь стоит 12000 руб. Сколько диван стоил до распродажи?
▼ Пусть х – первоначальная цена дивана. Составляем уравнение:
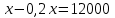, или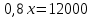 
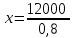= 15000 руб.
Таким образом, цена дивана до распродажи составляла 15000 рублей.
Ответ: 15000.▲
Задание 6. Цена изделия составляла 1000 руб. и была снижена на 10%, а затем еще на 20%. Какова окончательная цена товара?
▼ Окончательная цена товара: 0,9∙0,8∙1000 = 0,72∙1000 = 720 руб.▲
Задание 7. Изделие, цена которого 500 руб., сначала подорожала на 10%, а затем еще на 20%. Какова окончательная цена изделия?
▼ Окончательная цена изделия: 1,1∙1,2∙500 = 1,32∙500 = 660 руб.▲
Задание 8. Цену на некоторый товар сначала снизили на 30%, а затем повысили на 20%. На сколько процентов изменилась первоначальная цена товара?
▼ Пусть х – первоначальная цена товара. Окончательная цена товара: 0,7∙1,2х = 0,84х. Первоначальная цена товара изменилась на 0,84х – х =-0,16х, т.е. снизилась на 16% ▲
Задание 9. Цену товара повысили на 25%, затем новую цену повысили еще на 10% и, наконец, после перерасчета произвели повышение еще на 12%. На сколько процентов повысилась первоначальная цена товара?
▼ Пусть х – первоначальная цена товара. Окончательная цена товара: 1,25∙1,1∙1,12х = 1,54х. Первоначальная цена товара повысилась на 1,54х – х = 0,54х, или 54% ▲
Задание 10. Цену некоторого товара снизили на 15%, потом еще на 20%. Найти общий процент снижения цены?
▼ Пусть х – первоначальная цена товара. Новая цена товара: 0,85∙0,8х = 0,68х. Изменения цены 0,68х – х =- 0,32х, т.е. общий процент снижения цены составляет 32% ▲
Задание 11. Футболка стоила 800 рублей. После снижения цены она стала стоить 680 рублей. На сколько процентов была снижена цена на футболку?
▼ Изменения цены футболки равно 680 – 800 = -120, т.е. цена футболки снизилась на 120 руб., или на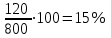
▲
Задание 12. Фрукты подешевели на 25%. Сколько фруктов можно теперь купить на те же деньги, на которые раньше покупали 3 кг?
▼ Пусть а – первоначальная цена; 3а – стоимость 3 кг фруктов по первоначальной цене; 0,75а – новая цена фруктов. По новой цене можно купить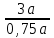
= 4 кг ▲
Задание 13. Бананы подорожали на 10%. Сколько бананов можно теперь купить на те же деньги, на которые раньше покупали 22 кг?
▼ Пусть а – первоначальная цена; 22а – стоимость 22 кг бананов по первоначальной цене; 1,1а – новая цена бананов. По новой цене можно купить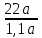
= 20 кг ▲
Задание 14. В сентябре 1 кг винограда стоил 60 рублей, в октябре виноград подорожал на 25%, а в ноябре еще на 20%. Сколько рублей стоил 1 кг винограда после подорожания в ноябре?
▼ После подорожания в ноябре 1 кг винограда стоил 60∙1,25∙1,2 = 90 руб.▲
Задание 15. Спрос на товар увеличился в пять раз. На сколько процентов увеличился спрос?
▼ Пусть а – первоначальный спрос, который принимаем за 100%. Составляем пропорции:
Спрос увеличился на 400% ▲
Задание 16. Объем товаров увеличился на 200%. Во сколько раз произошло увеличение?
▼ Пусть а – первоначальный объем товаров, который принимаем за 100%. Составляем пропорции:
Объем товаров увеличился в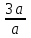
= 3 раза ▲
Задание 17. При повышении цены билета на 25% число зрителей в кинотеатре уменьшилось на 22%. На сколько процентов изменилась выручка кинотеатра?
▼ Пусть х – первоначальная цена билета, y – количество зрителей. Имеем:
xy – выручка до повышения;
1,25x∙0,78y = 0,975xy – выручка после повышения.
Выручка сократилась на 2,5% ▲
Задание 18. Цена первого товара повысилась на 30%, а потом еще на 5%.
Цена второго товара повысилась на 25%. После повышения цены товаров сравнялись. На сколько процентов первоначальная цена одного товара больше первоначальной цены другого товара?
▼ Пусть х, y – первоначальные цены товаров. Составляем уравнение:
, 
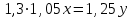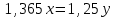
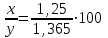= 91,6%▲
Задание 19. Зарплата была повышена два раза за один год на один и тот же процент. При таком повышении вместо 100 рублей за один день рабочий стал получать 125, 44 руб. На сколько процентов повысилась зарплата?
▼ Пусть y – процент повышения зарплаты. Составляем уравнение:
, 
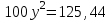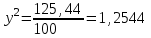
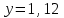, т.е. зарплата повысилась на 12% ▲
Задание 30.
Пример 2. Для путешествия был заготовлен запас продовольствия для 45 человек на 96 дней. На сколько дней хватит этот же запас продовольствия для 30 человек ?
▼ Составим схему по условию задачи:
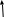  45 чел ------ 96 дн30 чел ------ х дн |
Зависимость обратно пропорциональная, так как если увеличить количество человек, то этот же запас продовольствия хватит на меньшее число дней. Условно обозначим такую зависимость разно направленными стрелками.
Запишем пропорцию:
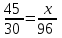
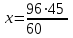= 144 дня.Ответ. 144 дня.▲
Задание 1. За 3,2 кг товара заплатили 11,52 р. Сколько следует заплатить за 1,5 кг этого товара?
▼ Составим схему по условию задачи:
 3,2 кг ------ 11,52 руб.1,5 кг ------ х руб. |
Зависимость между количеством товара и стоимостью покупки прямо пропорциональная, так как если купить товара в несколько раз больше, то и стоимость покупки увеличится во столько же раз. Условно обозначим такую зависи
Пример. Только 94% из 27 500 выпускников города правильно решили задачу B1. Сколько человек правильно решили задачу В1?
▼ Правильно решили задачу 27 500·0,94 = 25 850 учеников.▲
II. Нахождение числа по его процентам. Если известно, что a% числа х равно b, то число х находится по формуле
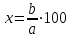. Например, если известно, что 12% числа равно 30, то искомое число 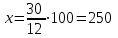.Пример. В школе французский язык изучают 124 учащихся, что составляет 25% от числа всех учащихся школы. Сколько учащихся в школе?
▼ Пусть х – число учащихся школы, тогда искомое число есть
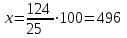▲Пример. Студентами технических вузов собираются стать 27 выпускников школы. Они составляют 30% от числа выпускников. Сколько в школе выпускников?
▼ Пусть х – число выпускников школы, тогда искомое число есть
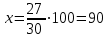▲III. Нахождение процентного отношения чисел. Чтобы найти процентное отношение двух чисел aи b, надо отношение этих чисел умножить на 100%, т.е. вычислить
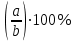. Например, сколько процентов составляет 120 от 60: ▼ 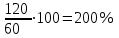▲В задачах часто говорится об изменении какой-либо величины на определенный процент. Что это значит?
Повышение цены на 10% означает, что к прежней цене х прибавили 0,1х, т.е. новая цена составит х + 0,1х = 1,1х.
Скидка на 25% означает, что прежняя цена х уменьшилась на 25%, т.е. новая цена составит х - 0,25х = 0,75х.
Правило: За 100% принимаем ту величину, с которой сравниваем.
Справедливы следующие утверждения:
• если величину хувеличить на p%, то получим х(1 + 0,01p);
• если величину хуменьшить на q%, то получим х(1 - 0,01q);
• если величину хувеличить на p%, а полученный результат уменьшить на q %, то получим
x(1 + 0,01p)(1 - 0,01q);
• если величину хдваждыувеличить на p%, то получим х(1+ 0,01p)2;
• если величину хдважды уменьшить на q%, то получим х(1- 0,01q)2;
• положенная в банк под p% годовых начальная сумма S0 через n лет с учетом процентов достигнет величины Sn = S0 (1 + 0,01p)n.
Задание 1. Учитель зарабатывает на 25% меньше, чем профессор. На сколько процентов больше, чем учитель, зарабатывает профессор?
▼ Если х - зарплата профессора, то х – 0,25х = 0,75х - зарплата учителя.
Профессор зарабатывает больше, чем учитель на 0,25х, или
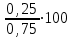= 33,3%.▲Задание 2. Цена на электрический чайник была повышена на 16% и составила 3480 рублей. Сколько рублей стоил чайник до повышения цены?
▼ Пусть х – первоначальная цена чайника. Составляем уравнение:
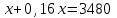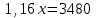
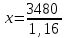, или = 3000 руб.Таким образом, цена чайника до повышения составляла 3000 рублей.
Ответ: 3000.▲
Задание 3. Пачка сливочного масла стоит 60 рублей. Пенсионерам магазин делает скидку 5%. Сколько рублей стоит пачка масла для пенсионера?
▼ Пачка сливочного масла для пенсионеров: 60·(1 - 0,05) = 57 руб.▲
Задание 4. Тетрадь стоит 24 рубля. Сколько рублей заплатит покупатель за 60 тетрадей, если при покупке больше 50 тетрадей магазин делает скидку 10% от стоимости всей покупки?
▼ Покупатель заплатит за 60 тетрадей со скидкой: 60·24∙(1 - 0,1) = 1296 руб.▲
Задание 5. В связи с распродажей диван подешевел на 20% и теперь стоит 12000 руб. Сколько диван стоил до распродажи?
▼ Пусть х – первоначальная цена дивана. Составляем уравнение:
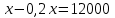, или 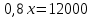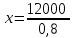= 15000 руб.Таким образом, цена дивана до распродажи составляла 15000 рублей.
Ответ: 15000.▲
Задание 6. Цена изделия составляла 1000 руб. и была снижена на 10%, а затем еще на 20%. Какова окончательная цена товара?
▼ Окончательная цена товара: 0,9∙0,8∙1000 = 0,72∙1000 = 720 руб.▲
Задание 7. Изделие, цена которого 500 руб., сначала подорожала на 10%, а затем еще на 20%. Какова окончательная цена изделия?
▼ Окончательная цена изделия: 1,1∙1,2∙500 = 1,32∙500 = 660 руб.▲
Задание 8. Цену на некоторый товар сначала снизили на 30%, а затем повысили на 20%. На сколько процентов изменилась первоначальная цена товара?
▼ Пусть х – первоначальная цена товара. Окончательная цена товара: 0,7∙1,2х = 0,84х. Первоначальная цена товара изменилась на 0,84х – х =-0,16х, т.е. снизилась на 16% ▲
Задание 9. Цену товара повысили на 25%, затем новую цену повысили еще на 10% и, наконец, после перерасчета произвели повышение еще на 12%. На сколько процентов повысилась первоначальная цена товара?
▼ Пусть х – первоначальная цена товара. Окончательная цена товара: 1,25∙1,1∙1,12х = 1,54х. Первоначальная цена товара повысилась на 1,54х – х = 0,54х, или 54% ▲
Задание 10. Цену некоторого товара снизили на 15%, потом еще на 20%. Найти общий процент снижения цены?
▼ Пусть х – первоначальная цена товара. Новая цена товара: 0,85∙0,8х = 0,68х. Изменения цены 0,68х – х =- 0,32х, т.е. общий процент снижения цены составляет 32% ▲
Задание 11. Футболка стоила 800 рублей. После снижения цены она стала стоить 680 рублей. На сколько процентов была снижена цена на футболку?
▼ Изменения цены футболки равно 680 – 800 = -120, т.е. цена футболки снизилась на 120 руб., или на
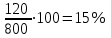▲Задание 12. Фрукты подешевели на 25%. Сколько фруктов можно теперь купить на те же деньги, на которые раньше покупали 3 кг?
▼ Пусть а – первоначальная цена; 3а – стоимость 3 кг фруктов по первоначальной цене; 0,75а – новая цена фруктов. По новой цене можно купить
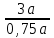= 4 кг ▲Задание 13. Бананы подорожали на 10%. Сколько бананов можно теперь купить на те же деньги, на которые раньше покупали 22 кг?
▼ Пусть а – первоначальная цена; 22а – стоимость 22 кг бананов по первоначальной цене; 1,1а – новая цена бананов. По новой цене можно купить
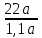= 20 кг ▲Задание 14. В сентябре 1 кг винограда стоил 60 рублей, в октябре виноград подорожал на 25%, а в ноябре еще на 20%. Сколько рублей стоил 1 кг винограда после подорожания в ноябре?
▼ После подорожания в ноябре 1 кг винограда стоил 60∙1,25∙1,2 = 90 руб.▲
Задание 15. Спрос на товар увеличился в пять раз. На сколько процентов увеличился спрос?
▼ Пусть а – первоначальный спрос, который принимаем за 100%. Составляем пропорции:
| а ---- 100% 5а ---- 500%  5а – а ---- 500% - 100%4а ---- 400% |
Спрос увеличился на 400% ▲
Задание 16. Объем товаров увеличился на 200%. Во сколько раз произошло увеличение?
▼ Пусть а – первоначальный объем товаров, который принимаем за 100%. Составляем пропорции:
| а ---- 100% а + 2а ---- 100% +200% 3а ---- 300% |
Объем товаров увеличился в
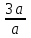= 3 раза ▲Задание 17. При повышении цены билета на 25% число зрителей в кинотеатре уменьшилось на 22%. На сколько процентов изменилась выручка кинотеатра?
▼ Пусть х – первоначальная цена билета, y – количество зрителей. Имеем:
| х ---- y 1,25х ---- 0,78 y |
xy – выручка до повышения;
1,25x∙0,78y = 0,975xy – выручка после повышения.
Выручка сократилась на 2,5% ▲
Задание 18. Цена первого товара повысилась на 30%, а потом еще на 5%.
Цена второго товара повысилась на 25%. После повышения цены товаров сравнялись. На сколько процентов первоначальная цена одного товара больше первоначальной цены другого товара?
▼ Пусть х, y – первоначальные цены товаров. Составляем уравнение:
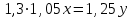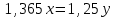
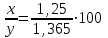, = 91,6%▲Задание 19. Зарплата была повышена два раза за один год на один и тот же процент. При таком повышении вместо 100 рублей за один день рабочий стал получать 125, 44 руб. На сколько процентов повысилась зарплата?
▼ Пусть y – процент повышения зарплаты. Составляем уравнение:
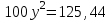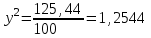
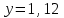, , т.е. зарплата повысилась на 12% ▲Задание 30.