ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 87
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Четыре одинаковые рубашки дешевле куртки на 8%. На сколько процентов пять таких же рубашек дороже куртки?
▼ Пусть x, y - стоимость одной рубашки и одной куртки соответственно. Примем стоимость одной куртки за 100%. Составляем уравнение: 4x = 0,92y. Значит стоимость одной рубашки составляет 0,92/4 = 0,23, или 23% стоимости куртки. Поэтому стоимость пяти рубашек составляет 5∙23 = 115% стоимости куртки. Это превышает стоимость куртки на 15%. ▲
Задание 31. Цена холодильника в магазине ежегодно уменьшается на одно и то же число процентов от предыдущей цены. Определите, на сколько процентов каждый год уменьшалась цена холодильника, если, выставленный на продажу за 20 000 рублей, через два года был продан за 15 842 рублей.
▼ Пусть цена холодильника ежегодно снижалась на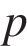
процентов в год. Составляем уравнение:
, 
, 
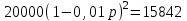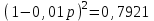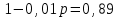р = 11%▲
Задание 32. Семья состоит из мужа, жены и их дочери-студентки. Если бы:
а) зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на 6,7%; б) если бы стипендия дочери уменьшилась втрое, общий доход семьи сократился бы на 4%. Сколько процентов от общего дохода семьи составляет зарплата жены?
▼ Нарисуем таблицу
Составляем уравнения:
.
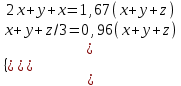Вычтем из обеих частей каждого уравнения сумму (x + y + z), получим
.
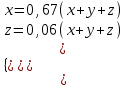Это значит: а) зарплата мужа составляет 67% от общего дохода семьи; б) стипендия дочки составляет 6% от общего дохода семьи.
Тогда зарплата жены составляет 100 – (67 + 6) = 27% общего дохода▲
Задание 20. Магазин в первый день продал 40% имеющихся овощей. За второй день он продал 80% овощей, проданных в первый день. В третий день – оставшиеся 28 кг. Сколько овощей было в магазине первоначально?
▼ Пусть х – вес первоначальных овощей. Составляем уравнение:
, 
, 
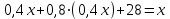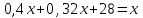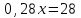
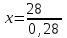= 100 кг▲
Задание 21. Поле вспахивали в течении трех дней. В первый день вспахали 56% всей площади. Во второй - 75% остатка, а в третий – 330 га. Какова площадь поля?
▼ Пусть х – площадь поля. Составляем уравнение:
, 
, 
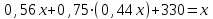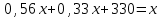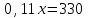
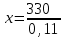= 3000 га▲
Задание 22. Квартплата составляла 2000 руб. Какой стала квартплата после ее увеличения на 20%?
▼ Квартплата после ее увеличения на 20% составляет 1,2∙2000 = 2400 руб.▲
Задание 23. Флакон шампуня стоит 160 рублей. Какое наибольшее число флаконов можно купить на 1000 рублей во время распродажи, когда скидка составляет 25% ?
▼ Во время распродажи шампунь станет стоить 160∙(1 − 0,25) = 120 руб.
Разделим 1000 на 120:
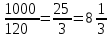. Значит, можно будет купить 8 флаконов шампуня.▲
Задание 24. Шариковая ручка стоит 40 рублей. Какое наибольшее число таких ручек можно будет купить на 900 рублей после повышения цены на 10%?
▼ После повышения цены ручка станет стоить 40∙(1 + 0,1) = 44 руб.
Разделим 900 на 44:
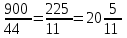. Значит, можно будет купить 20 ручек.▲
Задание 25. Сбербанк в конце года начисляет 4% годовых к сумме, находившейся на счету в конце года. Каким станет первоначальный вклад в 2500 руб. через один год?
▼ В конце года первоначальный вклад составит 2500∙(1 + 0,04) = 2600 руб.▲
Задание 26. Сбербанк в конце года начисляет 3% годовых к сумме, находившейся на счету в начале года. На сколько рублей увеличится первоначальный вклад в 1000 руб. через два года?
▼ В конце второго года первоначальный вклад составит 1000∙(1 + 0,03)
2 = 1000∙1,032 = 1000∙1,0609 = 1060,9 руб. Первоначальный капитал увеличился на 1060,9 – 1000 = 60,9 руб., или 6,09% ▲
Задание 27. Найти первоначальную сумму вклада, если после двух лет она выросла на 304,5 руб. при 3% годовых?
▼ Пусть х – первоначальная сумма вклада. Составляем уравнение:
, 
, 
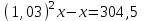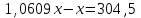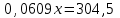
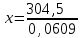= 5000 руб.▲
Задание 28. Найти первоначальную сумму вклада, если после трех лет она выросла на 765,1 руб. при 2% годовых?
▼ Пусть х – первоначальная сумма вклада. Составляем уравнение:
, 
, 
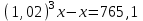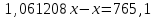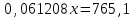
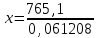= 12500 руб.▲
Задание 29. В понедельник акции компании подорожали на некоторое количество процентов, а во вторник подешевели на то же самое количество процентов. В результате они стали стоить на 4% дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?
▼ Пусть а - первоначальная стоимость акций, х – процент очередного изменения цены акции. Составляем уравнение:
, 
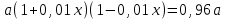х = 20% ▲
Задачи на числа
Задание 1. Найдите двузначное число, если частное от деления искомого числа на сумму его цифр равна 4, а частное от деления произведения его цифр на сумму цифр равно 2.
▼ Представим искомое число в виде 10y + x, где x – цифра единиц, y – цифра десятков. Составляем систему уравнений
, 
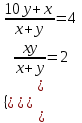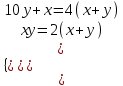x = 6, y = 3.
Искомое число 10y + x = 10∙3 + 6 = 36 ▲
Задание 2. Найдите двузначное число, если произведение его цифр в 6 раз меньше самого числа, а если к исходному числу прибавить 9, то получится число, написанное теми же цифрами, но в обратном порядке.
▼ Представим искомое число в виде 10y + x, где x – цифра единиц, y – цифра десятков. Составляем систему уравнений
, 
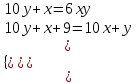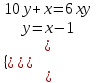x = 2, y = 1.
Искомое число 10y + x = 10∙1 + 2 = 12 ▲
Задачи на движение
Наиболее распространенный и эффективный способ решение задач на движение - использование таблиц.
Движение по прямой. Чаще всего в качестве переменной х удобнее всего выбирать скорость.
Пример 1. Из пунктов A в пункт B, расстояние между которыми 50 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 40 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 4 часа позже автомобилиста. Ответ дайте в км/ч.
▼ Обозначим за х – скорость велосипедиста. По условию задачи составим таблицу.
Составляем уравнение
.
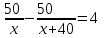
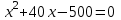
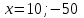Таким образом, скорость велосипедиста составляет 10 км/ч.
Ответ. 10▲
Пример 2. Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми 70 км. На следующий день он отправился обратно со скоростью на 3км/ч больше прежней. По дороге он сделал остановку на 3 часа. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.
▼ Обозначим за х – скорость велосипедиста из А в В. По условию задачи составим таблицу.
▼ Пусть x, y - стоимость одной рубашки и одной куртки соответственно. Примем стоимость одной куртки за 100%. Составляем уравнение: 4x = 0,92y. Значит стоимость одной рубашки составляет 0,92/4 = 0,23, или 23% стоимости куртки. Поэтому стоимость пяти рубашек составляет 5∙23 = 115% стоимости куртки. Это превышает стоимость куртки на 15%. ▲
Задание 31. Цена холодильника в магазине ежегодно уменьшается на одно и то же число процентов от предыдущей цены. Определите, на сколько процентов каждый год уменьшалась цена холодильника, если, выставленный на продажу за 20 000 рублей, через два года был продан за 15 842 рублей.
▼ Пусть цена холодильника ежегодно снижалась на
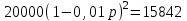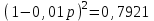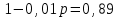процентов в год. Составляем уравнение: , , р = 11%▲Задание 32. Семья состоит из мужа, жены и их дочери-студентки. Если бы:
а) зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на 6,7%; б) если бы стипендия дочери уменьшилась втрое, общий доход семьи сократился бы на 4%. Сколько процентов от общего дохода семьи составляет зарплата жены?
▼ Нарисуем таблицу
| | муж | жена | дочь | Общий доход |
| В реальности | x | y | z | x + y + z |
| Ситуация а | 2x | y | z | 1,67(x + y + z) |
| Ситуация б | x | y | z/3 | 0,96(x + y + z) |
Составляем уравнения:
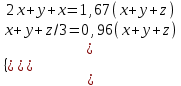.Вычтем из обеих частей каждого уравнения сумму (x + y + z), получим
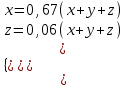.Это значит: а) зарплата мужа составляет 67% от общего дохода семьи; б) стипендия дочки составляет 6% от общего дохода семьи.
Тогда зарплата жены составляет 100 – (67 + 6) = 27% общего дохода▲
Задание 20. Магазин в первый день продал 40% имеющихся овощей. За второй день он продал 80% овощей, проданных в первый день. В третий день – оставшиеся 28 кг. Сколько овощей было в магазине первоначально?
▼ Пусть х – вес первоначальных овощей. Составляем уравнение:
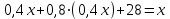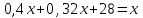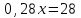
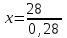, , = 100 кг▲Задание 21. Поле вспахивали в течении трех дней. В первый день вспахали 56% всей площади. Во второй - 75% остатка, а в третий – 330 га. Какова площадь поля?
▼ Пусть х – площадь поля. Составляем уравнение:
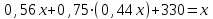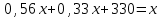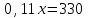
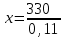, , = 3000 га▲Задание 22. Квартплата составляла 2000 руб. Какой стала квартплата после ее увеличения на 20%?
▼ Квартплата после ее увеличения на 20% составляет 1,2∙2000 = 2400 руб.▲
Задание 23. Флакон шампуня стоит 160 рублей. Какое наибольшее число флаконов можно купить на 1000 рублей во время распродажи, когда скидка составляет 25% ?
▼ Во время распродажи шампунь станет стоить 160∙(1 − 0,25) = 120 руб.
Разделим 1000 на 120:
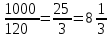. Значит, можно будет купить 8 флаконов шампуня.▲Задание 24. Шариковая ручка стоит 40 рублей. Какое наибольшее число таких ручек можно будет купить на 900 рублей после повышения цены на 10%?
▼ После повышения цены ручка станет стоить 40∙(1 + 0,1) = 44 руб.
Разделим 900 на 44:
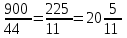. Значит, можно будет купить 20 ручек.▲Задание 25. Сбербанк в конце года начисляет 4% годовых к сумме, находившейся на счету в конце года. Каким станет первоначальный вклад в 2500 руб. через один год?
▼ В конце года первоначальный вклад составит 2500∙(1 + 0,04) = 2600 руб.▲
Задание 26. Сбербанк в конце года начисляет 3% годовых к сумме, находившейся на счету в начале года. На сколько рублей увеличится первоначальный вклад в 1000 руб. через два года?
▼ В конце второго года первоначальный вклад составит 1000∙(1 + 0,03)
2 = 1000∙1,032 = 1000∙1,0609 = 1060,9 руб. Первоначальный капитал увеличился на 1060,9 – 1000 = 60,9 руб., или 6,09% ▲
Задание 27. Найти первоначальную сумму вклада, если после двух лет она выросла на 304,5 руб. при 3% годовых?
▼ Пусть х – первоначальная сумма вклада. Составляем уравнение:
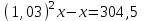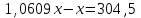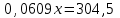
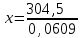, , = 5000 руб.▲Задание 28. Найти первоначальную сумму вклада, если после трех лет она выросла на 765,1 руб. при 2% годовых?
▼ Пусть х – первоначальная сумма вклада. Составляем уравнение:
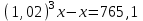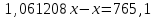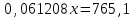
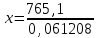, , = 12500 руб.▲Задание 29. В понедельник акции компании подорожали на некоторое количество процентов, а во вторник подешевели на то же самое количество процентов. В результате они стали стоить на 4% дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?
▼ Пусть а - первоначальная стоимость акций, х – процент очередного изменения цены акции. Составляем уравнение:
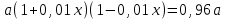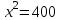, х = 20% ▲Задачи на числа
Задание 1. Найдите двузначное число, если частное от деления искомого числа на сумму его цифр равна 4, а частное от деления произведения его цифр на сумму цифр равно 2.
▼ Представим искомое число в виде 10y + x, где x – цифра единиц, y – цифра десятков. Составляем систему уравнений
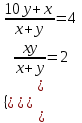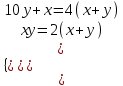, x = 6, y = 3.Искомое число 10y + x = 10∙3 + 6 = 36 ▲
Задание 2. Найдите двузначное число, если произведение его цифр в 6 раз меньше самого числа, а если к исходному числу прибавить 9, то получится число, написанное теми же цифрами, но в обратном порядке.
▼ Представим искомое число в виде 10y + x, где x – цифра единиц, y – цифра десятков. Составляем систему уравнений
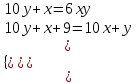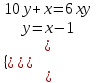, x = 2, y = 1.Искомое число 10y + x = 10∙1 + 2 = 12 ▲
Задачи на движение
Наиболее распространенный и эффективный способ решение задач на движение - использование таблиц.
| Скорость v | Время t | Расстояние S |
 |  |  |
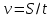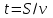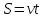Движение по прямой. Чаще всего в качестве переменной х удобнее всего выбирать скорость.
Пример 1. Из пунктов A в пункт B, расстояние между которыми 50 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 40 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 4 часа позже автомобилиста. Ответ дайте в км/ч.
▼ Обозначим за х – скорость велосипедиста. По условию задачи составим таблицу.
| | Скорость | Время | Расстояние | |
| Велосипедист | x | 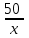 | 50 | Прибыл на 4 ч позже |
| Автомобилист | x + 40 | 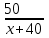 | 50 | |
Составляем уравнение
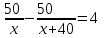
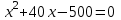
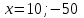.Таким образом, скорость велосипедиста составляет 10 км/ч.
Ответ. 10▲
Пример 2. Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми 70 км. На следующий день он отправился обратно со скоростью на 3км/ч больше прежней. По дороге он сделал остановку на 3 часа. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.
▼ Обозначим за х – скорость велосипедиста из А в В. По условию задачи составим таблицу.
| | Скорость | Время | Расстояние | |
| Туда | x | 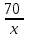 | 70 | |
| Обратно | x + 3 | 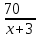 | 70 | Простой 3 ч |