ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 89
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Составляем уравнение
; 
;
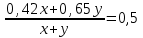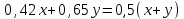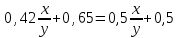
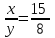, или x:y = 15:8.Таким образом, нужно взять сплавы в отношении 15:8.
Ответ: 15:8 ▲
Пример 17. К 40% -му раствору соляной кислоты добавили 50 г чистой кислоты, после чего концентрация раствора стала равной 60%. Найти первоначальный вес раствора?
▼ Пусть х – первоначальный вес раствора. Составляем таблицу:
| | Концентрация | Кислота г | Раствор г |
| I | 40% = 0,4 | 0,4x | x |
| II | 100% = 1 | 1∙50 | 50 |
| Итого | 60% = 0,6 | 0,4x+50 | х + 50 |
Составляем уравнение
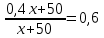x = 100.Таким образом, первоначальный вес раствора составляет 100 г.
Ответ: 100 ▲
Пример 18. Какое количество воды надо добавить к 2 л 18% -го раствора соли, чтобы получить 16% -ый раствор
▼ Пусть х – искомое количество воды. Составляем таблицу:
| | Концентрация | Соль л | Раствор л |
| I | 0 | 0 | x |
| II | 18% = 0,18 | 0,18∙2=0,36 | 2 |
| Итого | 16% = 0,16 | 0,36 | х + 2 |
Составляем уравнение
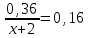x = 0,25.Таким образом, надо добавить 0,25 л воды.
Ответ: 0,25 ▲
Пример 19. Один сплав содержит два метала в отношении 2:3, другой сплав содержит те же металлы в отношении 3:4. Сколько частей каждого сплава надо взять, чтобы получит третий сплав, содержащий эти металлы в отношении 15:22?
▼ Пусть х, y – веса соответствующих сплавов. Составляем таблицу:
| | Металл 1 кг | Металл 2 кг | Сплав кг |
| I – (2:3) | 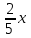 | 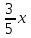 | х |
| II – (3:4) | 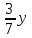 | 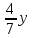 | y |
| Итого | 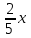+ 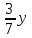| 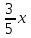+ 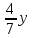| х + y |
Составляем уравнение
; 
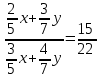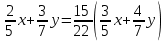
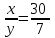, или x:y = 30:7.Таким образом, каждый металл нужно взять в отношении 30:7.
Ответ: 30:7 ▲
Пример 20. Имеются три смеси (I - III), составленные из трех элементов A, B и С. В первую смесь входят только элементы А и В в весовом отношении 1:2, во вторую смесь входят только элементы В и С в весовом отношении 1:3, в третью смесь входят только элементы А и С в весовом отношении 2:1. В каком отношении нужно взять эти смеси, чтобы во вновь полученной смеси элементы А, В и С содержались в весовом отношении 11:3:8?
▼ Пусть х, y, z– веса соответствующих смесей. Составляем таблицу:
| | Элемент А кг | Элемент В кг | Элемент С кг | Смесь кг |
| I - (1:2) | 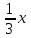 |  | | х |
| II - (1:3) | | 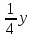 | 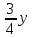 | y |
| III- (2:1) | 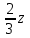 | | 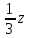 | z |
| Итого - (11:3:8) | 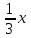+ 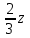| + 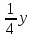| 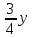+ 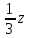| х + y + z |
По условию задачи в полученной смеси весовые отношения
А:В:С = 11:3:8, поэтому (
+
):( +
):(
+
) = 11:3:8.Составляем систему уравнений
; 
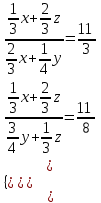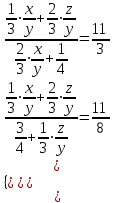.Обозначим
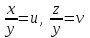, тогда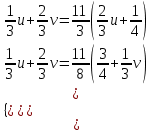
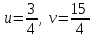. Это означает, что
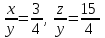, следовательно, x:y:z=3:4:15.Ответ: (3:4:15). ▲
Задание 1. Сергей смешал раствор, содержащий 20% кислоты и раствор, содержащий 40% той же кислоты. В итоге у него получился раствор, содержащий 32,5% кислоты, причём объём полученного раствора 4 литра. Сколько литров раствора, содержащего 20% кислоты, использовал Сергей при смешивании?
▼ Пусть х – количество исходного раствора. Составляем таблицу:
| | Концентрация | Кислота Л | Раствор л |
| I | 20% = 0,2 | 0,2x | x |
| II | 40% = 0,4 | 0,4(4 –x) | 4 - х |
| Итого | 32,5% = 0,325 | 1,6-0,2x | 4 |
Составляем уравнение
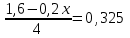x = 1,5.Таким образом, количество исходного раствора составляет 1,5 л.
Ответ: 1,5 ▲
Задание 2. Один газ в сосуде А содержал 21% кислорода, второй газ в сосуде В содержал 5% кислорода. Масса первого газа в сосуде А была больше массы второго газа в сосуде В на 300 г. Перегородку между сосудами убрали так, что газы перемешались и получившийся третий газ теперь содержит 14,6% кислорода. Найдите массу третьего газа. Ответ дайте в граммах.
▼ Пусть x – масса второго газа. Составляем таблицу:
| | Концентрация | Кислород Г | Газ г |
| I | 21% = 0,21 | 0,21(x+300) | x+300 |
| II | 5% = 0,05 | 0,05x | х |
| Итого | 14,6% = 0,146 | 0,26x+63 | 2x+300 |
Составляем уравнение
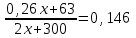x = 600.Таким образом, масса третьего газа равна 2х + 300 = 2∙600 + 300 =1500 г.
Ответ: 1500 ▲
Задание 3. Во сколько раз больше должен быть объём 5% -го раствора кислоты, чем объём 10% -го раствора той же кислоты, чтобы при смешивании получить 7% -ый раствор?
▼ Пусть х, y – объемы соответствующих растворов. Составляем таблицу:
| | Концентрация | Кислота Л | Раствор Л |
| I | 5% = 0,05 | 0,05x | Х |
| II | 10% = 0,1 | 0,1y | y |
| Итого | 7% = 0,07 | 0,05x+0,1y | х + y |
Составляем уравнение
; 
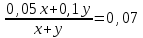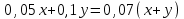
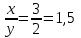.Таким образом, объем первого раствора должен быть больше второго в 1,5 раз.
Ответ: 1,5 ▲
Задание 4. Имеются два сплава. Первый сплав содержит 10% никеля, второй 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25 % никеля. Насколько кг масса первого сплава меньше массы второго?
▼ Пусть x, y - масса первого и второго сплава соответственно. Составляем таблицу:
| | Концентрация | Никель Кг | Сплав Кг |
| I | 10% = 0,1 | 0,1x | х |
| II | 30% = 0,3 | 0,3y | y |
| Итого | 25% = 0,25 | 0,1x+0,3y | 200 |
Составляем систему уравнений
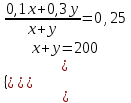x = 50, y =150.Таким образом, масса первого сплава меньше второго на 150 – 50 = 100 кг.
Ответ: 100 ▲
Задание 5. Смешали некоторое количество 15% -го раствора некоторого вещества с таким же количеством 19% -го процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
▼ Пусть х - масса первого раствора. Составляем таблицу:
| | Концентрация | Вещество Кг | Раствор кг |
| I | 15% = 0,15 | 0,15x | x |
| II | 19% = 0,19 | 0,19x | х |
| Итого | р%-? | 0,34x | 2x |
Составляем уравнение
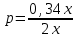= 0,17, или 17%.Таким образом, концентрация нового раствора равна 17%.
Ответ: 17 ▲
Задание 6. Смешали 4 литра 15% -го водного раствора с 6 литрами 25% -го водного раствора. Сколько процентов составляет концентрация получившегося раствора?
▼ Составляем таблицу:
| | Концентрация | Вещество Л | Раствор л |
| I | 15% = 0,15 | 0,15∙4=0,6 | 4 |
| II | 25% = 0,25 | 0,25∙6=1,5 | 6 |
| Итого | р% -? | 0,6+1,5=2,1 | 10 |