Файл: Методические указания по выполнению курсовой работы по дисциплине (модулю) Методы оптимальных решений.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 180
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
v1 = 6 и v4 =5 соответственно. Для неизвестного потенциала u3 нулевую поставку можно разместить в клетках (3, 1) и (3, 4), для которых известны те же потенциалы v1 = 6 и v4 =5 соответственно. Для неизвестного потенциала v2 нулевую поставку можно разместить в клетках (1, 2) и (4, 2), для которых известны потенциалы u1 = 0 и u4 = 1 соответственно. Для неизвестного потенциала v3 нулевую поставку можно разместить в клетках (1, 3) и (4, 3), для которых известны те же потенциалы u1 = 0 и u4 = 1 соответственно.
Среди клеток (2, 1), (2, 4), (3, 1), (3, 4), (1, 2), (4, 2), (1, 3) и (4, 3), в которых может быть размещена нулевая поставка, наименьший тариф имеет клетка (4, 3) с c43 = 6. Следовательно, нулевую поставку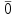 размещаем в клетку (4, 3), и она становится условно занятой и для нее выполняется условие u4 + v3 = c43, откуда v3 = c43 – u4 = 6 – (1) = 7:
размещаем в клетку (4, 3), и она становится условно занятой и для нее выполняется условие u4 + v3 = c43, откуда v3 = c43 – u4 = 6 – (1) = 7:
Для клетки (3, 3): u3 +
v3 = c33, откуда u3 = c33 – v3= 5 – 7 = –2:
Для клетки (3, 2): u3 + v2 = c32, откуда v2 = c32 – u3 = 14 – (–2) = 16:
Для клетки (2, 2): u2 + v2 = c22, , откуда u2 = c22 – v2= 7 – 16 = –9. Таким образом, найдены все значения потенциалов:
Вычисляем оценки свободных клеток:
12 = u1 + v2 c12 = 0 + 16 – 10 = 6 > 0,
13 = u1 + v3 c13 = 0 + 7 – 7 = 0,
14 = u1 + v4 c14 = 0 + 5 – 5 = 0,
21 = u2 + v1 c21 = – 9 + 6 – 10 = –13 < 0,
23 = u2 + v3 c23 = – 9 + 7 – 6 = –8 < 0,
24 = u2 + v4 c24 = – 9 + 5 – 9 = –13 < 0,
31 = u3 + v1 c31 = – 2 + 6 – 13 = –9 < 0,
34 = u3 + v4 c34 = – 2 + 5 – 7 = –4 < 0,
42 = u4 + v2 c42 = – 1 + 16 – 10 = 5 > 0.
В распределительной таблице оценки клеток проставлены в нижнем левом углу в скобках:
Получили две положительные оценки свободных клеток: 12 = 6 > 0 42 = 5 > 0. Следовательно, исходное опорное решение не является оптимальным и его можно улучшить.
Методика перехода к лучшему опорному решению
Наличие положительной оценки свободной клетки (ij ≥ 0) при проверке опорного решения на оптимальность свидетельствует о том, что полученное решение не оптимально, и для уменьшения значения целевой функции надо перейти к другому опорному решению. При этом надо перераспределять грузы, перемещая их из занятых клеток в свободные. Свободная клетка становится занятой, а одна из ранее занятых – свободной.
Для свободной клетки, имеющей максимальную положительную величину оценки,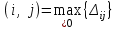 , строится цикл (цепь, многоугольник), все вершины которого, кроме одной, находятся в занятых клетках, углы прямые, число вершин четное. Форма цикла может быть разной, например:
, строится цикл (цепь, многоугольник), все вершины которого, кроме одной, находятся в занятых клетках, углы прямые, число вершин четное. Форма цикла может быть разной, например:

Но для клетки с положительной оценкой он является единственным.
Около свободной клетки цикла ставится знак (+), затем, используя правило чередования знаков, поочередно проставляют знаки (–) и (+). У вершин со знаком (–) выбирают минимальный груз = min[xij()], его прибавляют к грузам, стоящим у вершин со знаком (+), и отнимают от грузов у вершин со знаком (–). В результате перераспределения груза получим новое опорное решение. Это решение проверяем на оптимальность, и т.д. до тех пор, пока не получим оптимальное решение.
Замечание. В некоторых случаях поставка, перераспределяемая по циклу, может оказаться равной нулю. Это возможно тогда, когда клетка со знаком «–» содержала нулевую поставку . В этом случае по циклу передается нулевая поставка. В результате свободная клетка, для которой был построен цикл, становится заполненной (нулевой поставкой), а клетка с нулевой поставкой – свободной.
. В этом случае по циклу передается нулевая поставка. В результате свободная клетка, для которой был построен цикл, становится заполненной (нулевой поставкой), а клетка с нулевой поставкой – свободной.
Если при перераспределении поставки по циклу поставка обращается в нуль сразу в нескольких заполненных клетках, то свободной следует считать только одну (любую) из них. Остальные клетки, поставка в которых стала равной нулю, следует считать заполненными нулевой поставкой
 .
.
Переход к следующему опорному решению.
Выбираем клетку, от которой начнем построение цикла перераспределения поставок, по правилу , или
, или 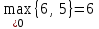 , т.е. максимальную величину оценки имеет свободная клетка (1, 2). Для этой клетки можно построить следующий цикл: 0*141
, т.е. максимальную величину оценки имеет свободная клетка (1, 2). Для этой клетки можно построить следующий цикл: 0*141 1550* (все вершины цикла, кроме первой, находятся в занятых клетках, углы прямые, число вершин четное). У вершин цикла с соответствующими значениями поставок по правилу чередования знаков ставим знаки (+) и (–).У вершин со знаком (–) выбираем минимальный груз = min[14,
1550* (все вершины цикла, кроме первой, находятся в занятых клетках, углы прямые, число вершин четное). У вершин цикла с соответствующими значениями поставок по правилу чередования знаков ставим знаки (+) и (–).У вершин со знаком (–) выбираем минимальный груз = min[14,  , 5] =
, 5] =  . Поскольку перемещаемый по циклу груз имеет нулевое значение, то произойдет только перемещение нулевой поставки
. Поскольку перемещаемый по циклу груз имеет нулевое значение, то произойдет только перемещение нулевой поставки  в клетку(1, 2), а клетка (4, 3), где ранее была нулевая поставка, станет свободной.
в клетку(1, 2), а клетка (4, 3), где ранее была нулевая поставка, станет свободной.
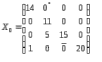
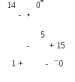
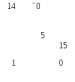
Фактически решение задачи (план перевозок) не изменилось, однако необходимо пересчитать потенциалы и найти новые оценки свободных клеток, учитывая, что клетка (1, 2) теперь занята, а клетка (4, 3) свободна:
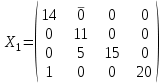 .
.
Проверка решения Х1 на оптимальность выполняется аналогично предыдущему шагу. Расчет потенциалов для занятых клеток:
u1 = 0;
клетка (1, 1): v1 = c11 – u1 = 6 – 0 = 6;
клетка (4, 1): u4 = c41 – v1 = 5 – 6 = 1;
клетка (1, 2): v2 = c12 – u1 = 10 – 0 = 10;
клетка (2, 2): u2 = c22 – v2 = 7 – 10 = 3;
клетка (3, 2): u3 = c32 – v2 = 14 – 10 = 4;
клетка (3, 3): v3 = c33 – u3 = 5 – 4 = 1;
клетка (4, 4): v4 = c44 – u4 = 4 – (1) = 5.
Расчет оценок свободных клеток:
13 = u1
Среди клеток (2, 1), (2, 4), (3, 1), (3, 4), (1, 2), (4, 2), (1, 3) и (4, 3), в которых может быть размещена нулевая поставка, наименьший тариф имеет клетка (4, 3) с c43 = 6. Следовательно, нулевую поставку
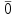 размещаем в клетку (4, 3), и она становится условно занятой и для нее выполняется условие u4 + v3 = c43, откуда v3 = c43 – u4 = 6 – (1) = 7:
размещаем в клетку (4, 3), и она становится условно занятой и для нее выполняется условие u4 + v3 = c43, откуда v3 = c43 – u4 = 6 – (1) = 7:| bj ai | 1 | 2 | 3 | 4 | ui | |
| 15 | 16 | 15 | 20 | |||
| 1 | 14 | 6 14 | 10 - | 7 - | 5 - | 0 |
| 2 | 11 | 10 - | 7 11 | 6 - | 9 - | |
| 3 | 20 | 13 - | 14 5 | 5 15 | 7 - | |
| 4 | 21 | 5 1 | 10 - | 6  | 4 20 | 1 |
| vj | 6 | | 7 | 5 | | |
Для клетки (3, 3): u3 +
v3 = c33, откуда u3 = c33 – v3= 5 – 7 = –2:
| bj ai | 1 | 2 | 3 | 4 | ui | |
| 15 | 16 | 15 | 20 | |||
| 1 | 14 | 6 14 | 10 - | 7 - | 5 - | 0 |
| 2 | 11 | 10 - | 7 11 | 6 - | 9 - | |
| 3 | 20 | 13 - | 14 5 | 5 15 | 7 - | –2 |
| 4 | 21 | 5 1 | 10 - | 6  | 4 20 | 1 |
| vj | 6 | | 7 | 5 | | |
Для клетки (3, 2): u3 + v2 = c32, откуда v2 = c32 – u3 = 14 – (–2) = 16:
| bj ai | 1 | 2 | 3 | 4 | ui | |
| 15 | 16 | 15 | 20 | |||
| 1 | 14 | 6 14 | 10 - | 7 - | 5 - | 0 |
| 2 | 11 | 10 - | 7 11 | 6 - | 9 - | |
| 3 | 20 | 13 - | 14 5 | 5 15 | 7 - | –2 |
| 4 | 21 | 5 1 | 10 - | 6  | 4 20 | 1 |
| vj | 6 | 16 | 7 | 5 | | |
Для клетки (2, 2): u2 + v2 = c22, , откуда u2 = c22 – v2= 7 – 16 = –9. Таким образом, найдены все значения потенциалов:
| bj ai | 1 | 2 | 3 | 4 | ui | |
| 15 | 16 | 15 | 20 | |||
| 1 | 14 | 6 14 | 10 - | 7 - | 5 - | 0 |
| 2 | 11 | 10 - | 7 11 | 6 - | 9 | –9 |
| 3 | 20 | 13 | 14 5 | 5 15 | 7 - | –2 |
| 4 | 21 | 5 1 | 10 - | 6  | 4 20 | 1 |
| vj | 6 | 16 | 7 | 5 | | |
Вычисляем оценки свободных клеток:
12 = u1 + v2 c12 = 0 + 16 – 10 = 6 > 0,
13 = u1 + v3 c13 = 0 + 7 – 7 = 0,
14 = u1 + v4 c14 = 0 + 5 – 5 = 0,
21 = u2 + v1 c21 = – 9 + 6 – 10 = –13 < 0,
23 = u2 + v3 c23 = – 9 + 7 – 6 = –8 < 0,
24 = u2 + v4 c24 = – 9 + 5 – 9 = –13 < 0,
31 = u3 + v1 c31 = – 2 + 6 – 13 = –9 < 0,
34 = u3 + v4 c34 = – 2 + 5 – 7 = –4 < 0,
42 = u4 + v2 c42 = – 1 + 16 – 10 = 5 > 0.
В распределительной таблице оценки клеток проставлены в нижнем левом углу в скобках:
| bj ai | 1 | 2 | 3 | 4 | ui | |
| 15 | 16 | 15 | 20 | |||
| 1 | 14 | 6 14 | 10 (6) | 7 (0) | 5 (0) | 0 |
| 2 | 11 | 10 (–13) | 7 11 | 6 (–8) | 9 (–13) | –9 |
| 3 | 20 | 13 (–9) | 14 5 | 5 15 | 7 (–4) | –2 |
| 4 | 21 | 5 1 | 10 (5) | 6  | 4 20 | 1 |
| vj | 6 | 16 | 7 | 5 | | |
Получили две положительные оценки свободных клеток: 12 = 6 > 0 42 = 5 > 0. Следовательно, исходное опорное решение не является оптимальным и его можно улучшить.
Методика перехода к лучшему опорному решению
Наличие положительной оценки свободной клетки (ij ≥ 0) при проверке опорного решения на оптимальность свидетельствует о том, что полученное решение не оптимально, и для уменьшения значения целевой функции надо перейти к другому опорному решению. При этом надо перераспределять грузы, перемещая их из занятых клеток в свободные. Свободная клетка становится занятой, а одна из ранее занятых – свободной.
Для свободной клетки, имеющей максимальную положительную величину оценки,
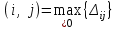 , строится цикл (цепь, многоугольник), все вершины которого, кроме одной, находятся в занятых клетках, углы прямые, число вершин четное. Форма цикла может быть разной, например:
, строится цикл (цепь, многоугольник), все вершины которого, кроме одной, находятся в занятых клетках, углы прямые, число вершин четное. Форма цикла может быть разной, например:
Но для клетки с положительной оценкой он является единственным.
Около свободной клетки цикла ставится знак (+), затем, используя правило чередования знаков, поочередно проставляют знаки (–) и (+). У вершин со знаком (–) выбирают минимальный груз = min[xij()], его прибавляют к грузам, стоящим у вершин со знаком (+), и отнимают от грузов у вершин со знаком (–). В результате перераспределения груза получим новое опорное решение. Это решение проверяем на оптимальность, и т.д. до тех пор, пока не получим оптимальное решение.
Замечание. В некоторых случаях поставка, перераспределяемая по циклу, может оказаться равной нулю. Это возможно тогда, когда клетка со знаком «–» содержала нулевую поставку
 . В этом случае по циклу передается нулевая поставка. В результате свободная клетка, для которой был построен цикл, становится заполненной (нулевой поставкой), а клетка с нулевой поставкой – свободной.
. В этом случае по циклу передается нулевая поставка. В результате свободная клетка, для которой был построен цикл, становится заполненной (нулевой поставкой), а клетка с нулевой поставкой – свободной. Если при перераспределении поставки по циклу поставка обращается в нуль сразу в нескольких заполненных клетках, то свободной следует считать только одну (любую) из них. Остальные клетки, поставка в которых стала равной нулю, следует считать заполненными нулевой поставкой
 .
.Переход к следующему опорному решению.
Выбираем клетку, от которой начнем построение цикла перераспределения поставок, по правилу
 , или
, или 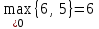 , т.е. максимальную величину оценки имеет свободная клетка (1, 2). Для этой клетки можно построить следующий цикл: 0*141
, т.е. максимальную величину оценки имеет свободная клетка (1, 2). Для этой клетки можно построить следующий цикл: 0*141 1550* (все вершины цикла, кроме первой, находятся в занятых клетках, углы прямые, число вершин четное). У вершин цикла с соответствующими значениями поставок по правилу чередования знаков ставим знаки (+) и (–).У вершин со знаком (–) выбираем минимальный груз = min[14,
1550* (все вершины цикла, кроме первой, находятся в занятых клетках, углы прямые, число вершин четное). У вершин цикла с соответствующими значениями поставок по правилу чередования знаков ставим знаки (+) и (–).У вершин со знаком (–) выбираем минимальный груз = min[14,  , 5] =
, 5] =  . Поскольку перемещаемый по циклу груз имеет нулевое значение, то произойдет только перемещение нулевой поставки
. Поскольку перемещаемый по циклу груз имеет нулевое значение, то произойдет только перемещение нулевой поставки  в клетку(1, 2), а клетка (4, 3), где ранее была нулевая поставка, станет свободной.
в клетку(1, 2), а клетка (4, 3), где ранее была нулевая поставка, станет свободной.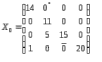
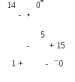
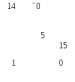
Фактически решение задачи (план перевозок) не изменилось, однако необходимо пересчитать потенциалы и найти новые оценки свободных клеток, учитывая, что клетка (1, 2) теперь занята, а клетка (4, 3) свободна:
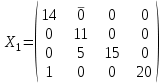 .
.Проверка решения Х1 на оптимальность выполняется аналогично предыдущему шагу. Расчет потенциалов для занятых клеток:
u1 = 0;
клетка (1, 1): v1 = c11 – u1 = 6 – 0 = 6;
клетка (4, 1): u4 = c41 – v1 = 5 – 6 = 1;
клетка (1, 2): v2 = c12 – u1 = 10 – 0 = 10;
клетка (2, 2): u2 = c22 – v2 = 7 – 10 = 3;
клетка (3, 2): u3 = c32 – v2 = 14 – 10 = 4;
клетка (3, 3): v3 = c33 – u3 = 5 – 4 = 1;
клетка (4, 4): v4 = c44 – u4 = 4 – (1) = 5.
Расчет оценок свободных клеток:
13 = u1