Файл: Задача Расчеты на прочность и жесткость круглых пластин при осесимметричном изгибе.docx

Из 3-го и 4-го 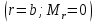граничных условий получаем систему уравнений: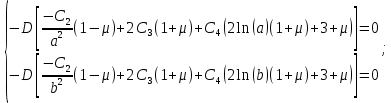





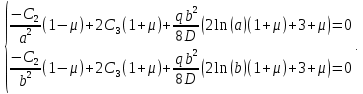
Вычтем из 2-го уравнения 1-ое и получим:







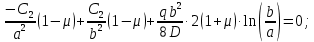
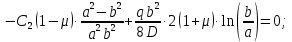
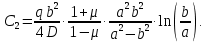
Подставив в первое уравнение, получим: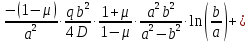









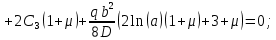
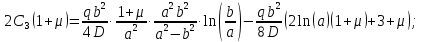
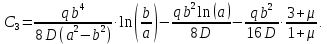
Подставляем постоянные , и в уравнение прогиба с учетом 2-го граничного условия :









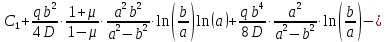
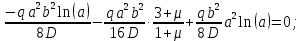
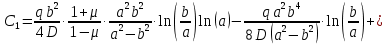
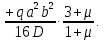
Уравнение наклона:





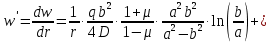
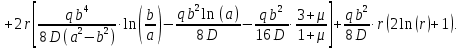
Уравнение прогиба:

---

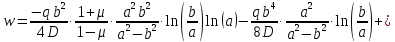
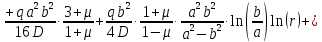
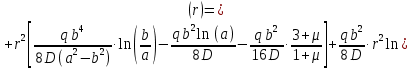
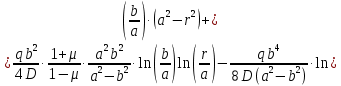
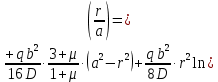
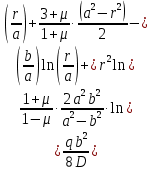
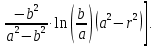
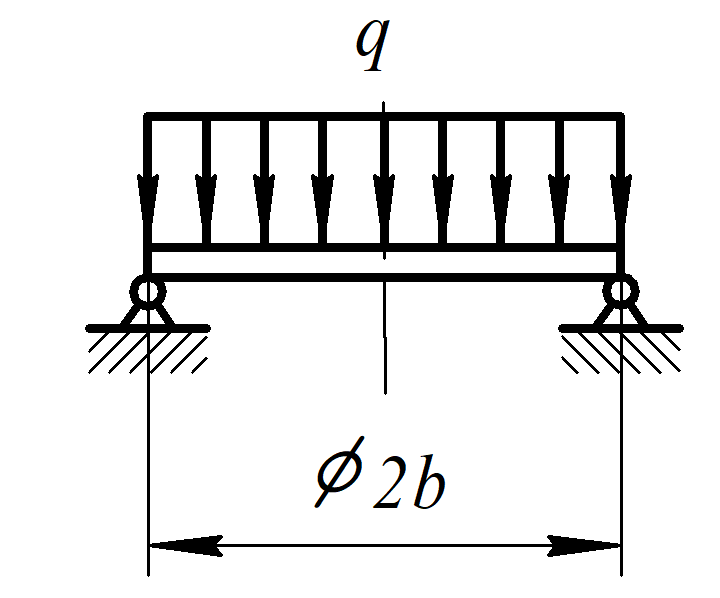
Рисунок 3 Третья часть расчетной схемы.


Для определения постоянных интегрирования запишем четыре граничных условия:

1. 
   
   
2. 
   
   
3. 
   
   
4. 
   
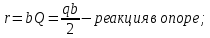
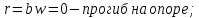
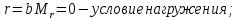
     1   2   3

---

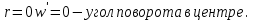
Из 1-го граничного условия получим:



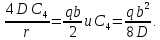
Уравнение наклона с учетом 4-го граничного условия :



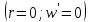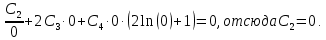
Уравнение момента:







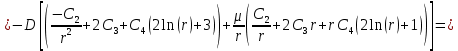
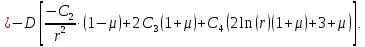
С учетом 3-го граничного условия и известных и :







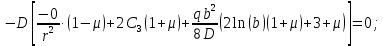
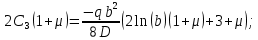
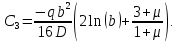
Запишем уравнение прогиба с учетом 2-го граничного условия 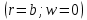и найденных , и и найдем :







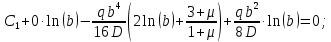
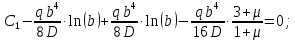
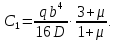
Уравнение наклона:









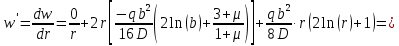
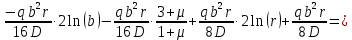
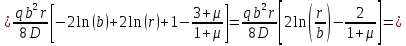
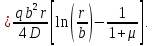
Уравнение прогиба:

---

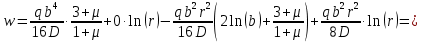
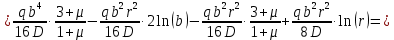
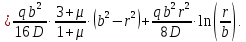
Уравнение наклона на внутренней границе от момента :



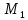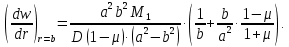
Уравнение наклона на внутренней границе от силы :



















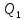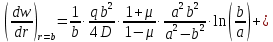
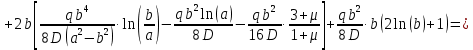
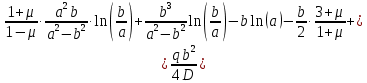
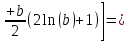
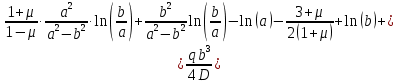
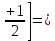
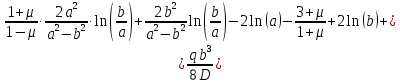
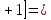
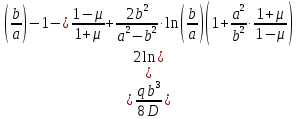
Уравнение наклона на внутренней границе от силы :



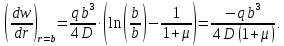
В следствие того, что внутренняя часть пластинки изогнута по сферической поверхности, наклон на границе будет равен:



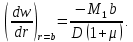
Из этих 4-х уравнений получим :























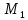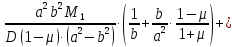
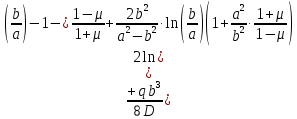
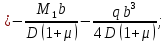
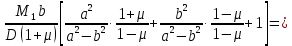
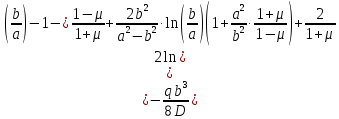
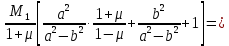
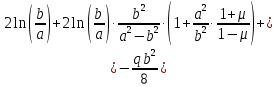
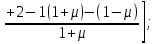
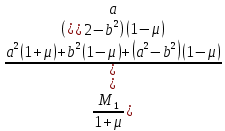
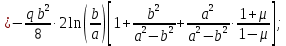
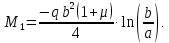
Подставив значение 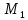в уравнение прогиба от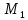

---

и сложив с уравнением прогиба от силы , получим уравнение прогиба на участке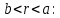



















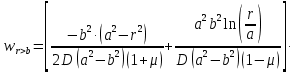
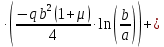
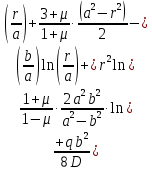
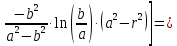
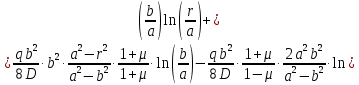
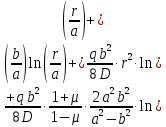
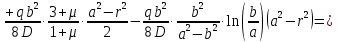
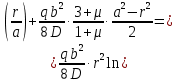
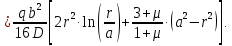
Подставив в уравнение прогиба на участке 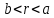значение 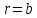, получим прогиб под нагрузкой: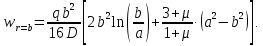





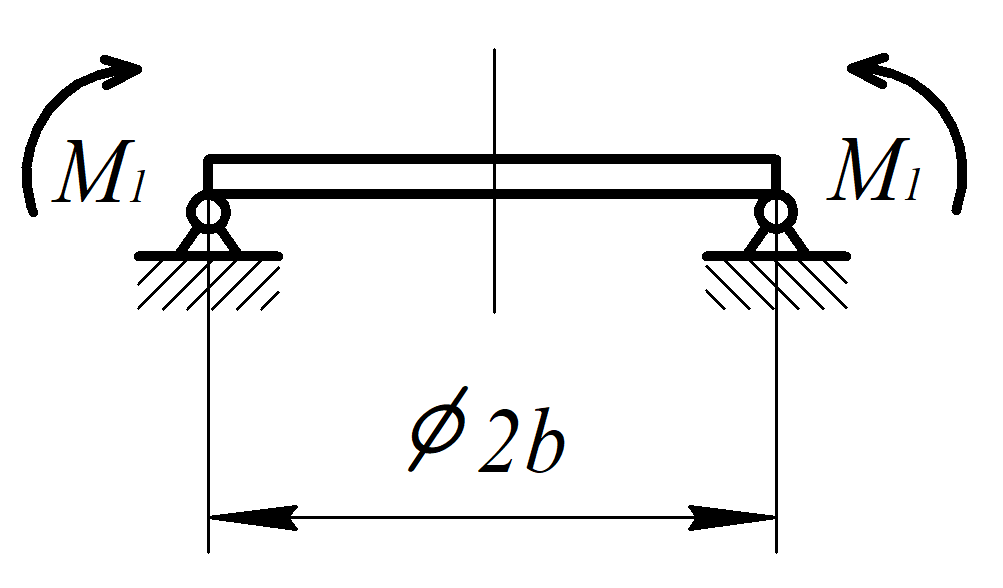
Рисунок 4 Четвертая часть расчетной схемы.


Для определения постоянных интегрирования запишем четыре граничных условия:

1. 
   ;
   
2. 
   
   
3. 
   
   
4. 
   
   

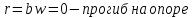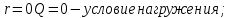
Определим поперечную силу:









Из 3-го граничного условия 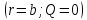получим:

---