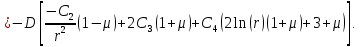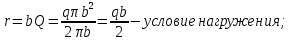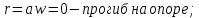Файл: Задача Расчеты на прочность и жесткость круглых пластин при осесимметричном изгибе.docx

Введение

Элементы конструкций в виде пластин и оболочек вращения широко применяются в ракетостроении, авиастроении. В частности, такими элементами являются днища, корпуса, камеры сгорания, баки ракеты, воздушные и газовые баллоны. Распространение элементов в виде пластин и оболочек вращения вызвано их малым весом, рациональностью геометрических форм, хорошей технологичностью и экономичностью изготовления, высокой прочностью и жесткостью.

В ракетостроении и авиастроении важными критериями являются условия прочности и жесткости, в следствии того, что в процессе полёта конструкция летательного аппарата должна перенести аэродинамические нагрузки без повреждений и изменений формы.

Напряженно-деформированное состояние тонкостенных элементов более сложное, чем теория напряженного состояния бруса, поэтому в курсе «Сопротивление материалов» почти не рассматривается.

Расчет на жесткость и прочность включает в себя следующие этапы: выбор расчетной схемы, определение внутренних усилий, построение эпюр и определение величины максимально допустимой внешней нагрузки. Исходными данными для расчета являются взаимосвязь между геометрическими параметрами конструкции, свойства материала и допустимый уровень нагружения.

Цель данной курсовой работы - овладение методиками расчета на прочность и жесткость пластин и оболочек при различных способах нагружения, приобретение и закрепление уже имеющийся умений проведения расчета на прочность и жесткость элементов конструкции ракетной техники.

Задача 1. Расчеты на прочность и жесткость круглых пластин при осесимметричном изгибе

Постановка задачи:

Произвести расчет круглой пластины при осесимметричном изгибе.

Таблица 1 – Исходные данные.

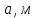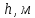		Сталь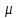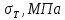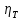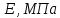
0,65	0,024	09Г2С	0,31	370	2,7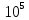

---

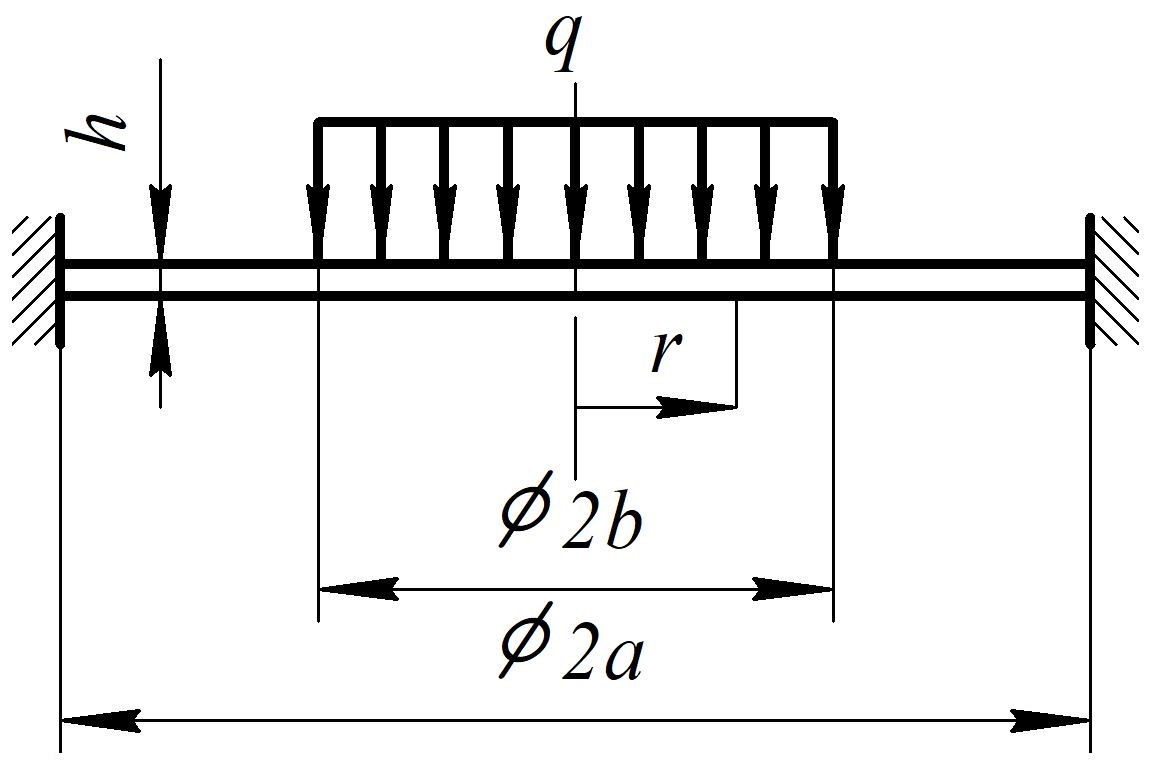
Рисунок 1 Расчетная схема круглой пластины.


Дано:

• 
  расчетная схема 8;
  
• 
  геометрические размеры: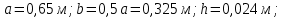
  
• 
  материал: сталь 09Г2С; ; ;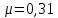
  
• 
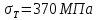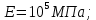
  допускаемый прогиб: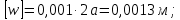
  
• 
  коэффициент запаса прочности: .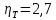
  

Требуется:

• 
  построить эпюры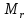 и 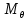в долях ;
  
• 
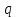  построить эпюру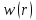 в долях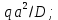
  
• 
  определить допускаемую распределенную нагрузку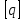 , удовлетворяющий условиям прочности и жесткости пластины.
  

Решение:

Определение функции прогиба срединной поверхности пластины:

При осесимметричном изгибе дифференциальное уравнение срединной поверхности круглой пластины имеет вид:



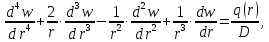
где 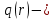закон изменения распределенной нагрузки;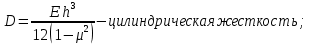



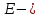модуль упругости (модуль Юнга);

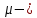коэффициент Пуассона.

Общее решение уравнения:



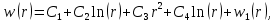
где 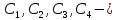константы интегрирования.

Частное решение имеет вид:

---

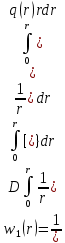
Вследствие того, что на пластину не действует поперечная нагрузка, то частное решение 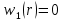и уравнение срединной поверхности принимает вид: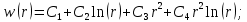



Разбиваем пластинку, как показано на рисунке 2 и определяем функцию прогиба для каждой ее части.



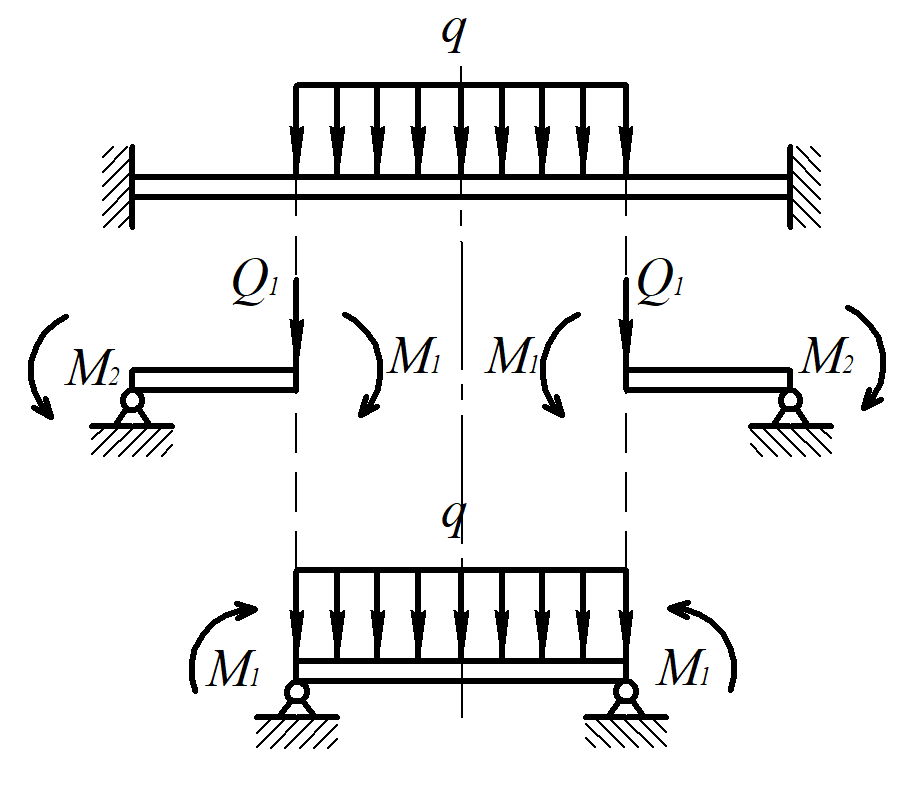
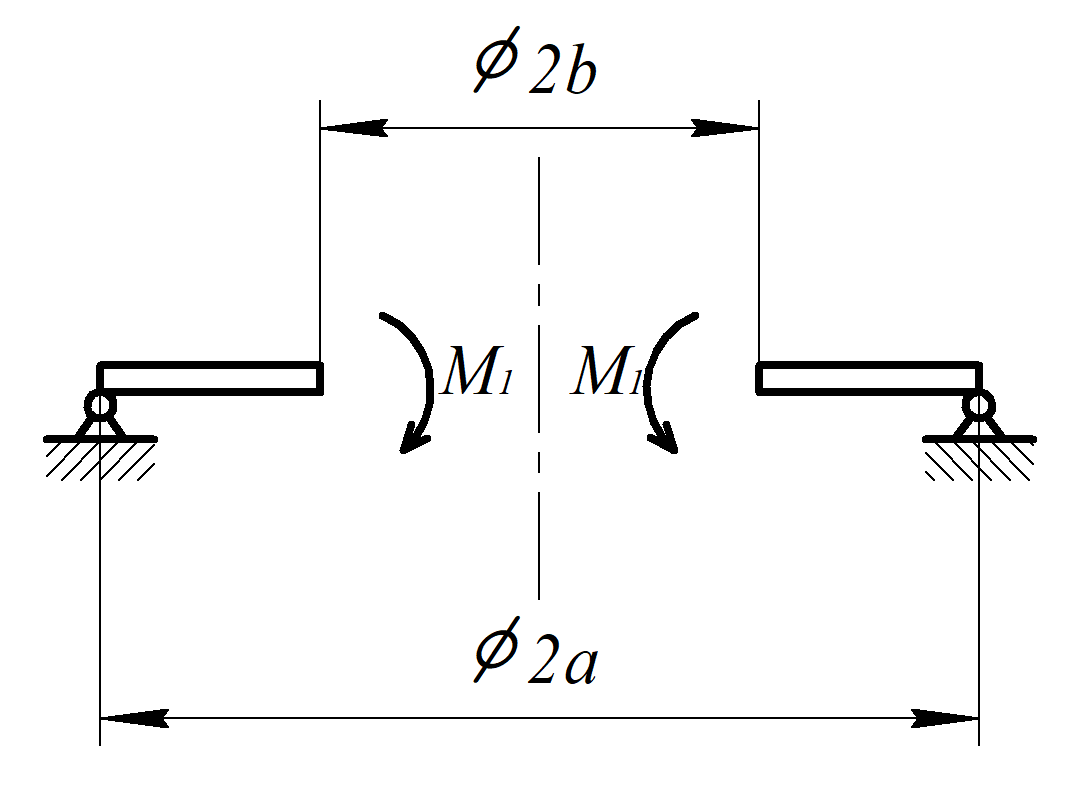
Рисунок 3 Первая часть расчетной схемы.

Рисунок 2 Разбиение круглой пластины.


Для определения постоянных интегрирования 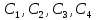запишем четыре граничных условия:

1. 
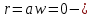   прогиб на опоре;
   
2. 
   
   
3. 
   
   
4. 
   
   

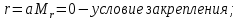
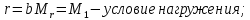
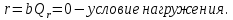
Находим производные:













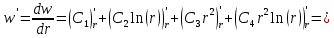
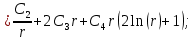
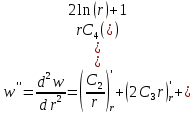
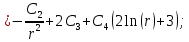
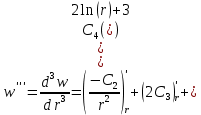
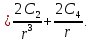
Определяем поперечную силу в окружном сечении:









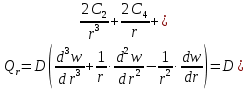
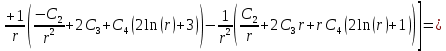
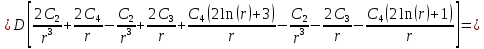
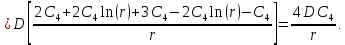
Из 4-го граничного условия ( 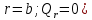получаем: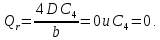

---

Находим изгибающий момент в окружном сечении:







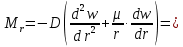
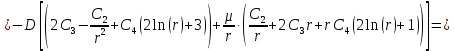
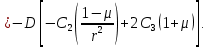
Из 2-го 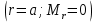и 3-го 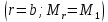граничных условий получаем систему из 2-х уравнений: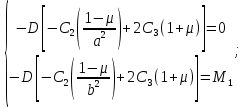









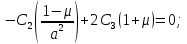
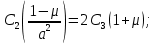
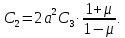
Подставив 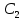во второе уравнение, получим: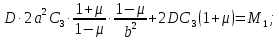









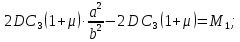
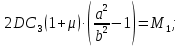
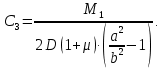
Подставляем 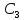в уравнение :


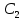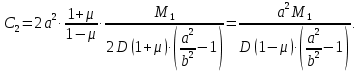
Уравнение прогиба с учетом найденных постоянных 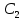, 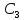и 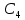имеет следующий вид: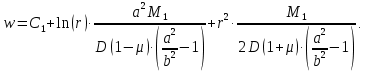



Из 1-го граничного условия 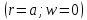получим: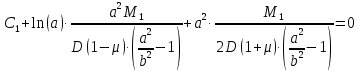







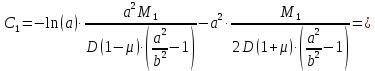
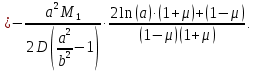
Уравнение наклона с учетом найденных постоянных , ,

---

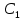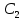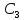
и имеет следующий вид: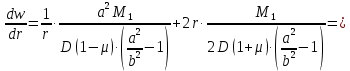







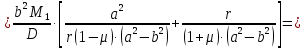
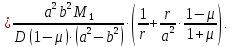
Уравнение прогиба с учетом найденных постоянных , , и имеет следующий вид: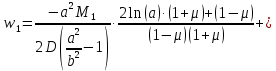


















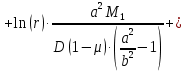
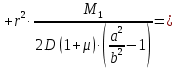
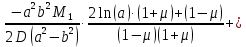
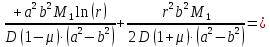
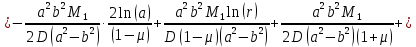
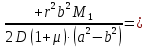
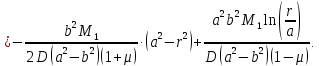
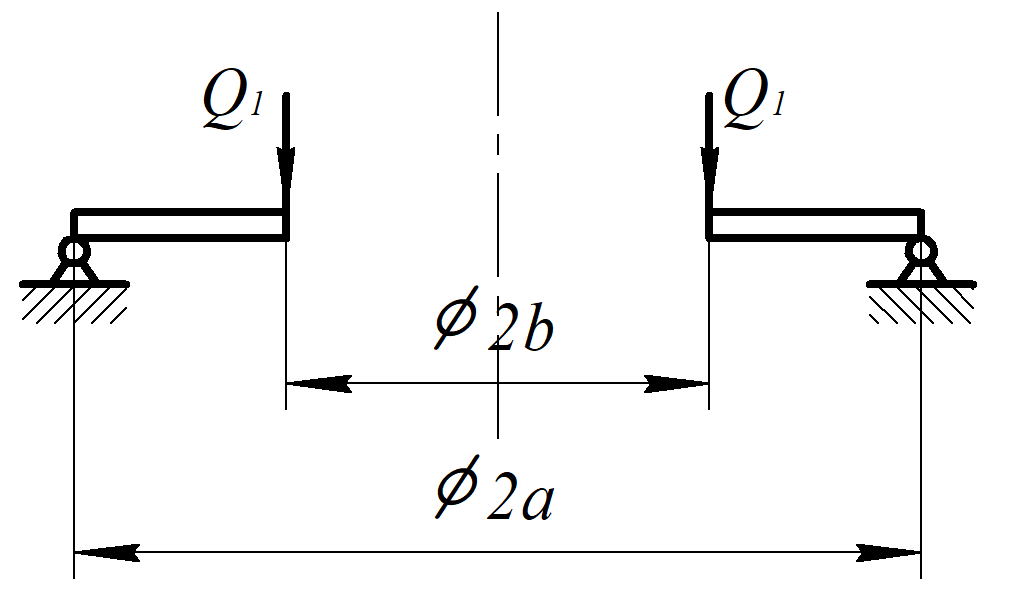
Рисунок 2 Вторая часть расчетной схемы.


Для определения постоянных интегрирования запишем четыре граничных условия:

1. 
   
   
2. 
   
   
3. 
   
   
4. 
   
   

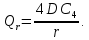
Из 1-го граничного условия 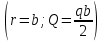получим:

---