Файл: Задача Расчеты на прочность и жесткость круглых пластин при осесимметричном изгибе.docx

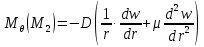– уравнение изгибающего момента характерного для схемы, изображенной на рисунке 7. Подставляем в уравнение постоянные , и , ранее определенные для данной схемы: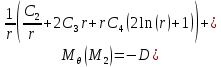











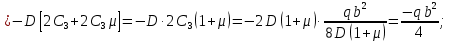
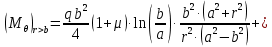
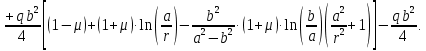
Момент в центральной части:



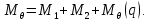
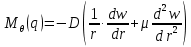– уравнение изгибающего момента характерного для схемы, изображенной на рисунке 5. Подставляем в уравнение постоянные , и , определенные для данной схемы: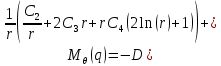

---

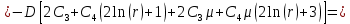
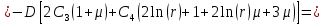
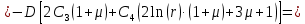
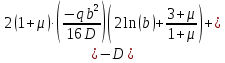
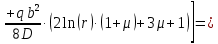
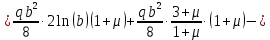
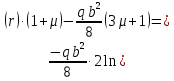
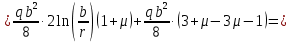
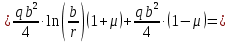
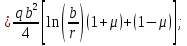
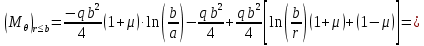
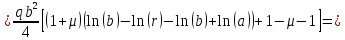
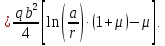
Функции прогиба срединной поверхности при











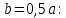
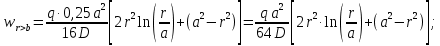
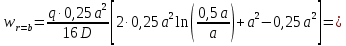
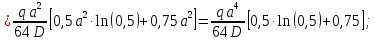
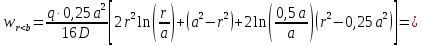
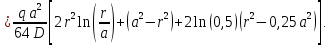
Функции распределенного изгибающего момента при

:

















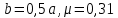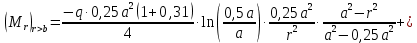
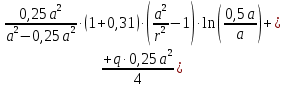
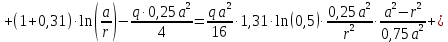
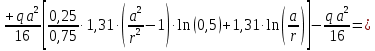
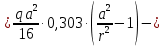
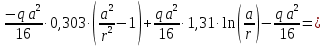
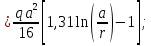
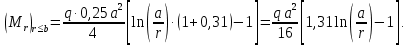
Функции распределенного изгибающего момента при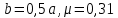

:













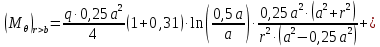
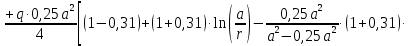
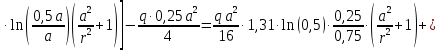
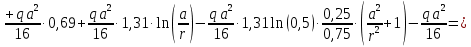
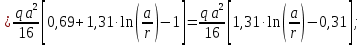
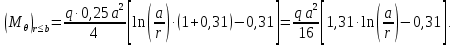
По формулам находим величины 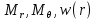для ряда значений 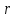. Результаты представлены в таблице.

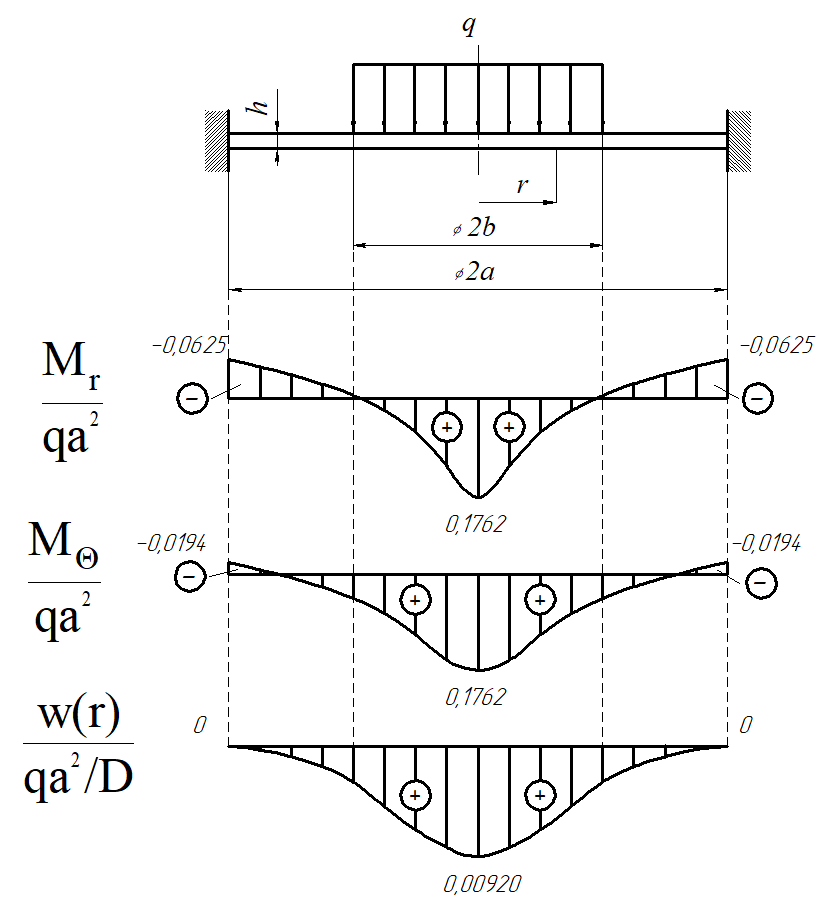Таблица 2 – Результаты расчета круглой пластины.

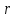	0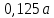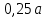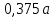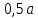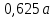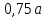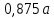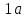
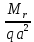	0,1762	0,1078	0,0510	0,0178	-0,0057	-0,0240	-0,0389	-0,0516	-0,0625
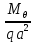	0,1762	0,1509	0,0941	0,0609	0,0374	0,0191	0,0042	-0,0084	-0,0194
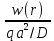	0,0092	0,0082	0,0068	0,0049	0,0027	0,0016	0,0008	0,0002	0,0000

---

Рисунок 6 Эпюры.


Анализ эпюр и показывает, что опасными будут наиболее удаленные от срединной плоскости нижние точки в центре пластины.
В окрестности опасной точки выделим элементарный объем.



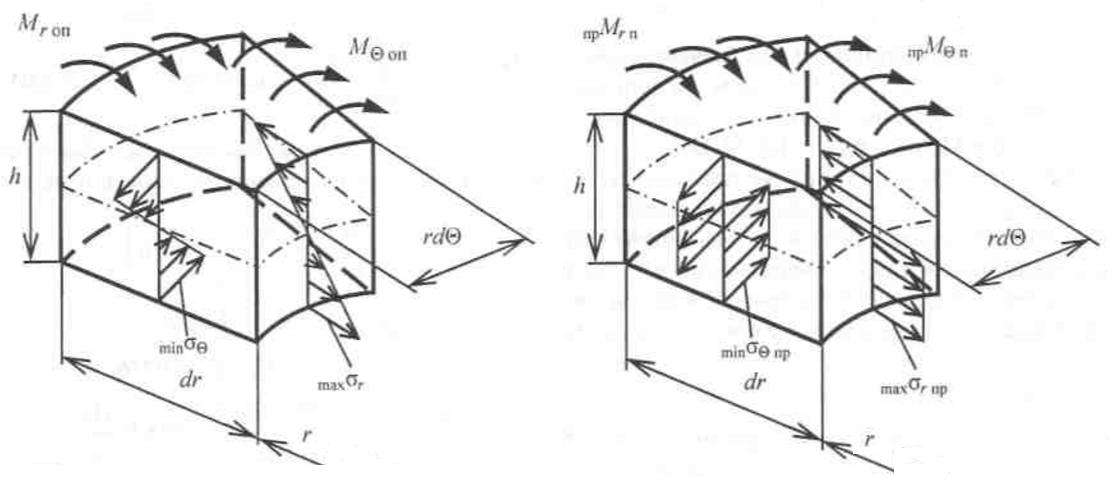
Рисунок 7 Внутренние силовые факторы.


Экстремальные напряжения в опасных точках:



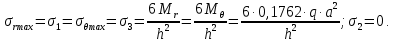
В соответствии с четвертой теорией прочности:









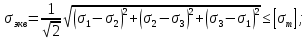
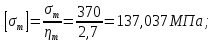
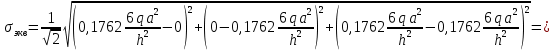
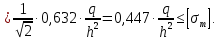
Из условия прочности допускаемое давление:



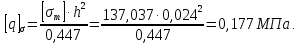
Проверяем условие жесткости:







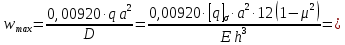
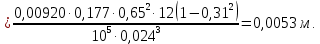
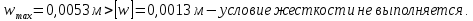
Вычисляем допускаемое давление из условия жесткости пластины:







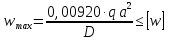
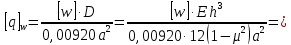
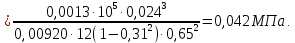
Окончательно принимаем минимальное значение давления:



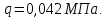
Вычисляем рабочие напряжения в опасной точке:



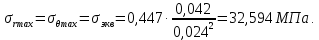
Выводы и результаты:

• 
  построены эпюры распределенных изгибающих моментов в окружном и радиальном сечениях, также построена эпюра прогибов (рисунок 8). Анализ эпюр показал, что опасными сечениями являются наиболее удаленные от срединной плоскости нижние точки в центре пластины. Значения моментов , , прогиба и возникающих внутренних напряжений 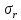, 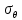увеличиваются при увеличении диаметра пластины;
  
• 
  полученное из условия прочности давление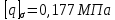 не удовлетворяет заданному условию жесткости. Давление, которое удовлетворяет условиям прочности и жесткости, равняется: 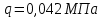. Величина допускаемого давления зависит от применяемого материала, для того чтобы достичь заданного условия жесткость необходимо применить материал с большим модулем Юнга 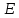. При увеличении модуля Юнга 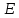уменьшается прогиб пластины;
  

---

• 
  рабочее напряжение в опасной точке пластины: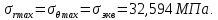 Возникающие внутренние напряжения , прямо пропорциональны давлению и обратно пропорциональны толщине пластины .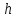
  

Данный метод расчета можно использовать для таких элементов конструкции ракеты, как донная защита и днища баков, также данная схема может использоваться в качестве примера полезного груза, который расположен в головной части ракеты. При полете полезный груз давит на ракету по ее диаметру.

Характер нагружения исходной расчетной схемы соответствует состоянию нижней части ГО, на которую действует полезный груз.

Так как между полезным грузом и створками ГО присутствует зазор, то расчет, приведенный в данной работе, можно использовать для вычисления расчета на прочность и жесткость данного элемента ракеты.


Рисунок 8 Зависимость значения от диаметра пластины .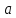



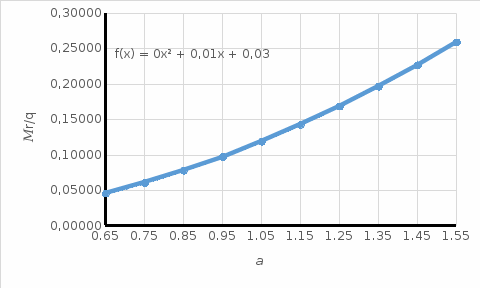
Рисунок 9 Зависимость значения от коэффициента Пуассона .



Рисунок 10 Зависимость значения от диаметра пластины .

---

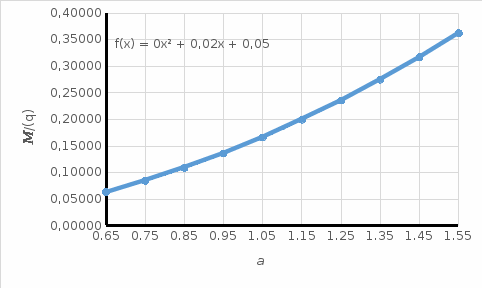
Рисунок 11 Зависимость значения от коэффициента Пуассона .





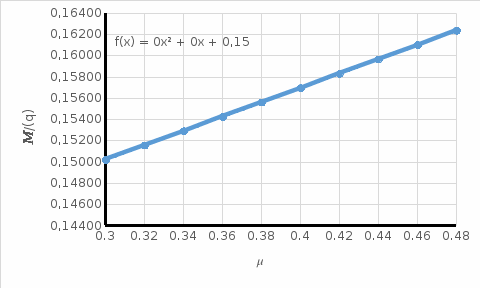
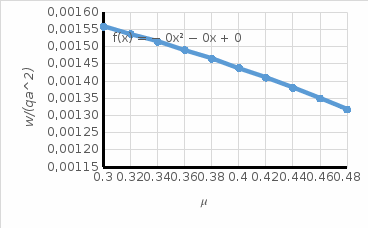
Рисунок 13 Характер изменения значения прогиба 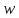от коэффициента Пуассона .

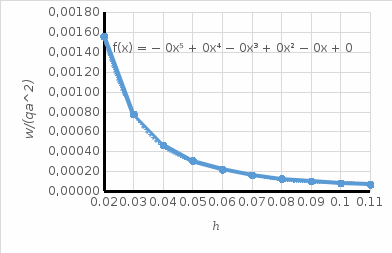
Рисунок 14 Характер изменения значения прогиба 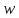от толщины пластины .

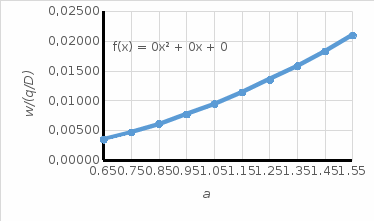
Рисунок 12 Характер изменения значения прогиба от диаметра пластины .

---