Министерство Транспорта РФФилиал ФТОУ ВПО « Морская Государственная Академия имени Адмирала Ф.Ф. Ушакова » в г. Ростове-на-ДонуРяды. Ряды Фурье.Сборник задач по высшей математике.Ростов-на-Дону2008г.§1. Числовые ряды. Достаточные признаки сходимости ряда и его суммы.

1. 
   Определение ряда и его суммы.
   

Определение 1. Пусть задача бесконечная последовательность чисел.u₁, u₂, u₃,..., u_n,...Выражение u₁+u₂+…..+u_n+…. называется числовым рядомПри этом числа u₁, u₂,..., u_n,... называются членами ряда.Коротко ряд записывается так : Выражение для n-го члена ряда при произвольном n называется общим членом ряда.Ряд считается заданным, если известно правило, по которому для любого номера n можно записать соответствующий член ряда. Чаще всего общий член ряда задается формулой , например, если , то ряд имеет вид: Определение 2. 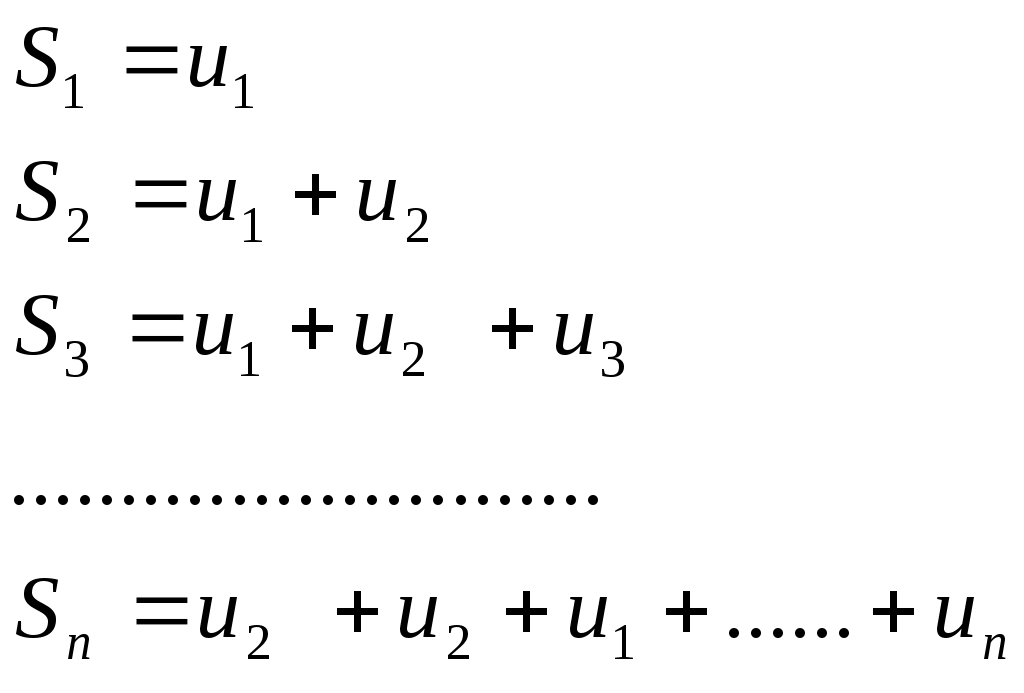Сумма конечного числа n первых членов ряда называется n-ой частичной суммой ряда: Образуем последовательность частичных сумм ряда: Определение 3. Если существует конечный предел последовательности частичных сумм членов данного ряда при n ,то ряд называется сходящимся, а число S-его суммой. Это записывается так.Если последовательность не стремится к пределу, то ряд называется расходящимся. Это возможно в двух случаях:

1. 
   Если последовательность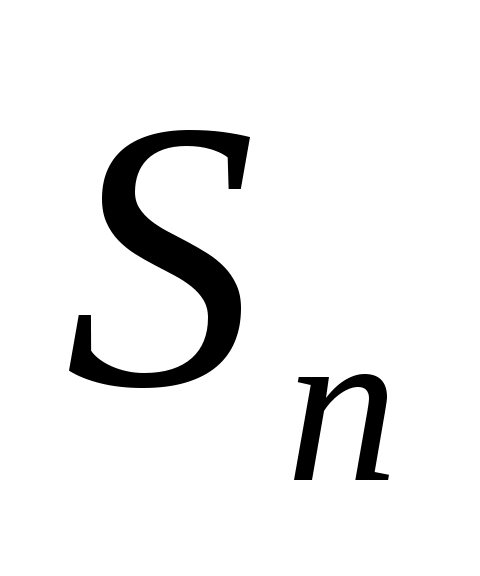
   
2. 
   Если последовательность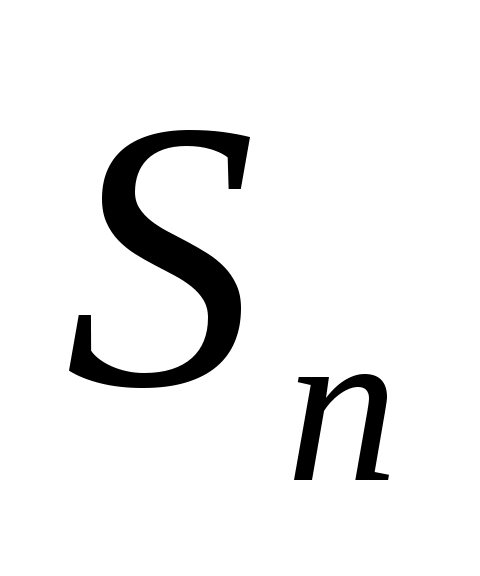 колеблющаяся (т.е. не имеет предела ни конечного, ни бесконечного).
   

---

В качестве простого примера рассмотрим сумму членов бесконечной геометрической прогрессии: Сумма n первых членов Если , то , по этому , т.е.При бесконечная геометрическая прогрессия образует сходящийся ряд, сумма которого .a значит, ряд расходится. Если , получится ряд и т.д., т.е. - колеблющаяся последовательность, не стремящаяся ни к какому пределу, ряд расходится.Следовательно, бесконечная геометрическая прогрессия представляет ряд, который сходится при и расходится при .1.2. Свойства сходящихся рядов.Теория 1. Если ряд сходится и имеет сумму , то ряд , (2)где С - какое-либо фиксированное число, также сходится и его сумма равна .Теория 2 Если сходятся рядыи их суммы, соответственно, равны и

---

, то также сходятся и ряды



причем их суммы, соответственно, равны и .

Теория 3. Если ряд сходится, то сходится и ряд, полученный из данного путем приписывания или отбрасывания любого конечного числа членов, т.е на сходимость ряда не влияет отбрасывания конечного числа его членов.

3. 
   Необходимый признак сходимости ряда. Гармонический ряд
   

Теорема. Если ряд сходится, то его n-й член стремится к нулю при неограниченном возрастание n: Следствие. Если n-й член ряда не стремится к нулю при n , то ряд расходится.Например, ряд расходится, т.к. Рассмотрим гармонический ряд: Тем не менее, докажем, что ряд расходится.Напишем гармонический ряд подробнее:Напишем вспомогательный ряд:Обозначим сумму n членов гармонического ряда (1), а сумму n членов ряда (2).Так как каждый член ряда (1) больше или равен соответствующему члену уряда (2), то для Подсчитаем частичные суммы ряда (2) для n, равных

---

:

,







Следовательно,

При достаточно большом может быть сделано больше любого положительного числа, т.е.

,

то тогда, поскольку , т.е. гармонический ряд расходится.
1.4 Ряды с положительными членами. Достаточные признаки сходимости.
Будем рассматривать ряды с положительными членами, или, так называемые знакоположительные ряды:



1. Признаки сравнения.

Теорема 1. Пусть имеем двазнакоположительных ряда:



Если хотя бы начиная с некоторого номера n члены ряда (1) не больше соответствующих членов ряда (2): ,

и ряд (2) сходится, то сходится и ряд (1).

Пример. Исследуем на сходимость ряд:

Рассмотрим вспомогательный ряд:

Он сходится как сумма геометрической прогрессии со знаменателем . Сравним его члены с членами исходного ряда:



Очевидно, что . Следовательно, исходный ряд является сходящимся в соответствии с теоремой 1 настоящего пункта.

---

Теорема 2. Если члены знакоположительного ряданачиная хотя бы с некоторого номера не меньше соответствующих членов расходящегося знакоположительного ряда.т.е. , то и ряд (1) расходится.Пример. Исследуем на сходимость ряд . Запишем его в виде:Рассмотрим вспомогательный ряд:Этот ряд расходится, т.к. это гармонический ряд( то, что отброшен первый член, на сходимость не влияет). Члены ряда (1) не меньше соответствующих членов расходящегося ряда (2), следовательно, по теореме 2 ряд (1) расходится.Теорема 3. (Предельный признак сравнения.) Если знакоположительные ряды (1) и (2) таковы, что существует конечный предел ,то из сходимости ряда (2) следует сходимость ряда (1), а из расходимости ряда (2) следует расходимость ряда (1).Предельный признак сравнения чаще всего применяется к рядам, общие члены которых является отношениями многочленов.При использовании признаков сравнения исследуемый ряд часто сравнивается или с бесконечной геометрической прогрессией (см. п. 1.1), или с обобщенным гармоническим рядом:который сходится при и расходится при Пример. Исследовать на сходимость ряды.1)

---

Смотрите также файлы

• Теория вероятностей.doc

• Суть стартапа, что это такое.docx

• История Болезни Ф. И. О. больного Чуркин Сергей Геннадьевич 17 лет. Диагноз.doc

• Олимпиада по русскому языку i тур Найди общее начало для частей слов, которые находятся справа, и впиши его.docx

• Основные значения сигналов, подаваемых светофорами (независимо от места установки и их назначения), следующие.pdf