Файл: Сборник задач по высшей математике. РостовнаДону 2008г. 1.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 62
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
;
249)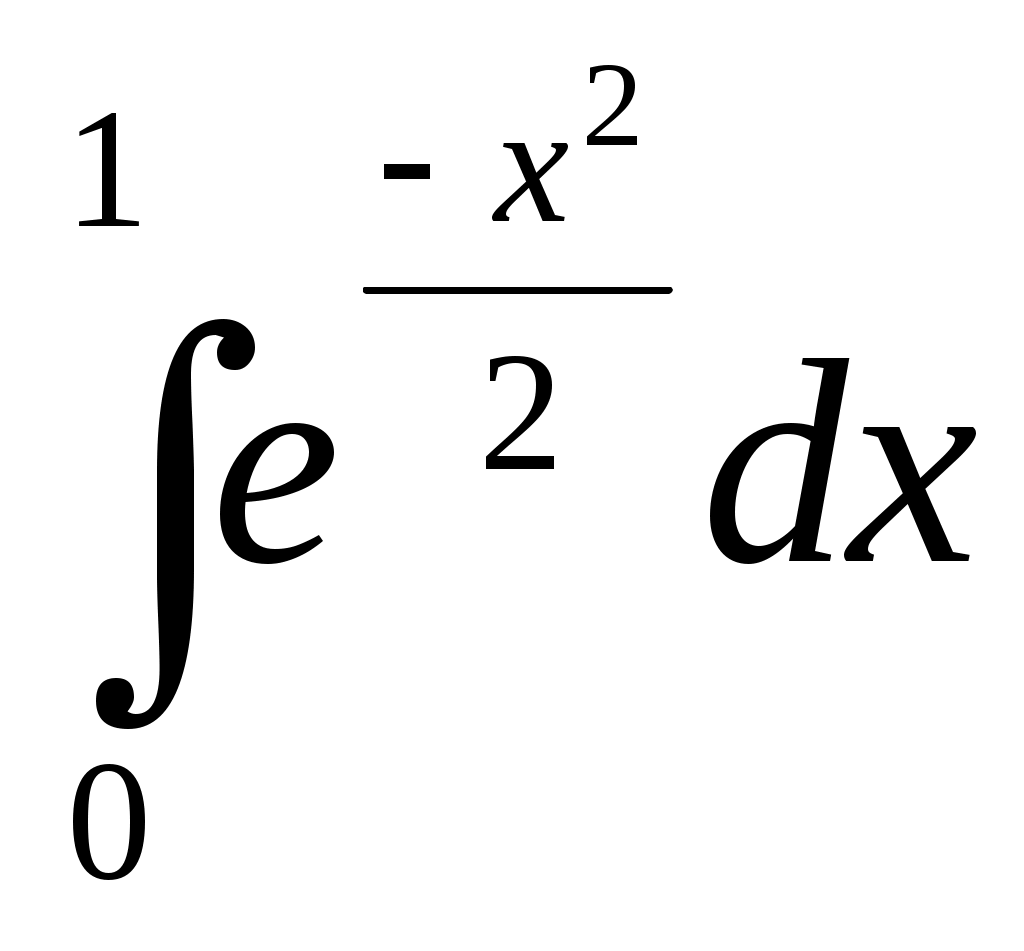 ;
;
250)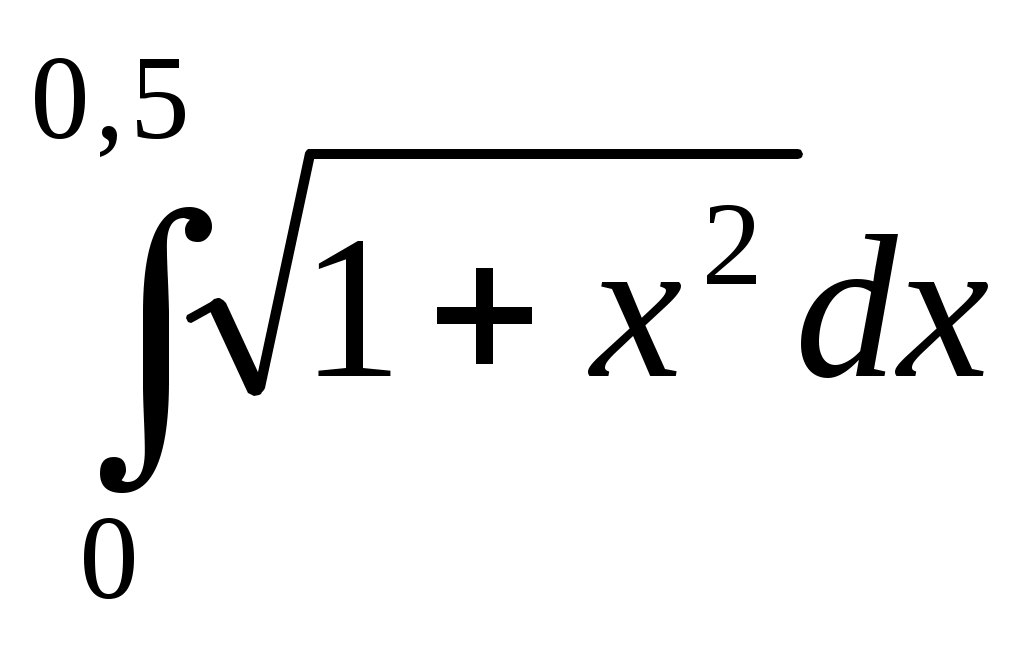 ;
;
251)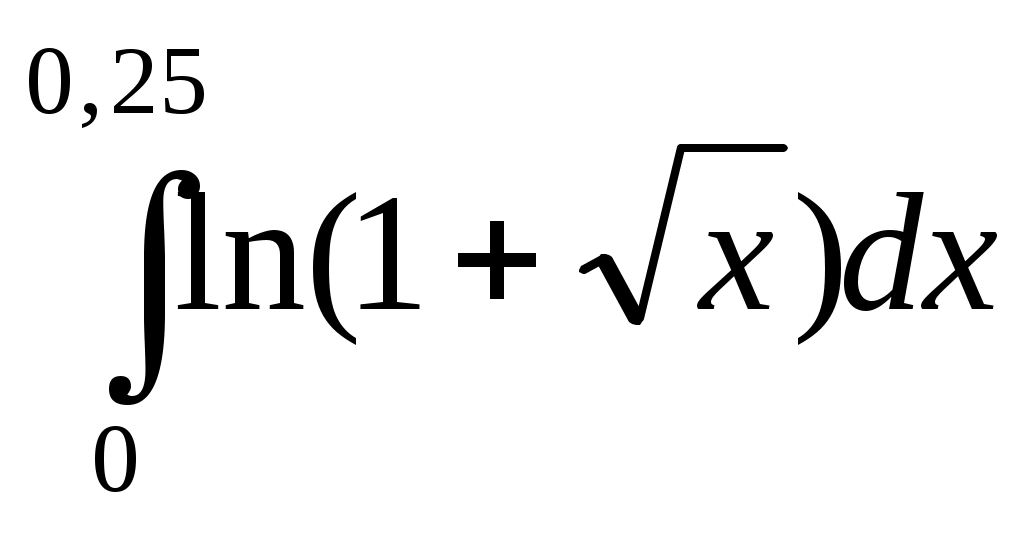 ;
;
252)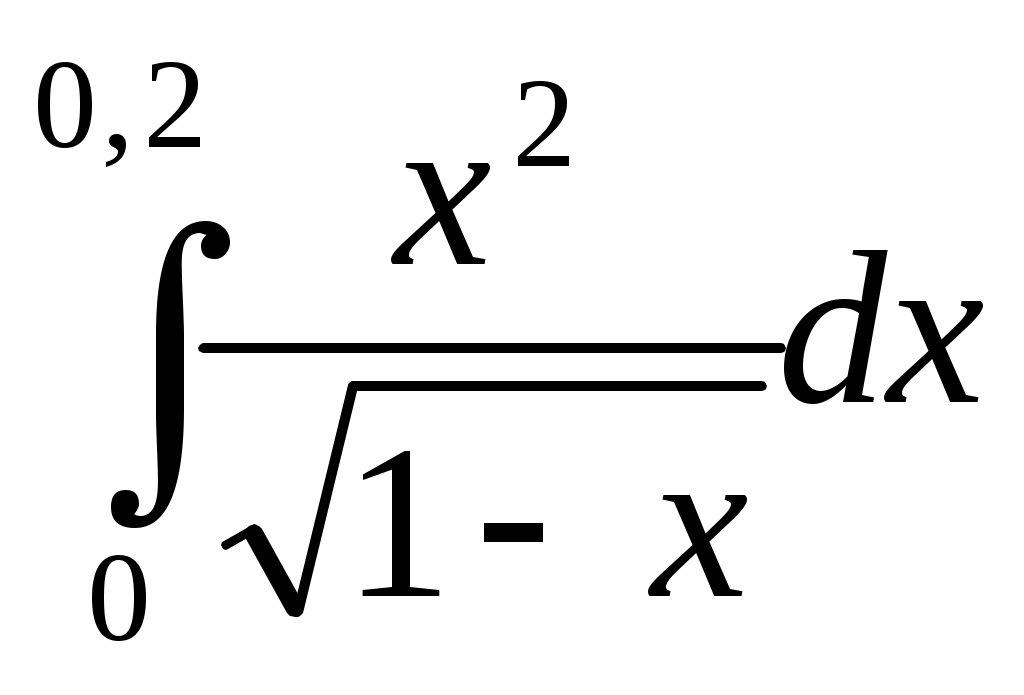 , δ=10-4;
, δ=10-4;
253)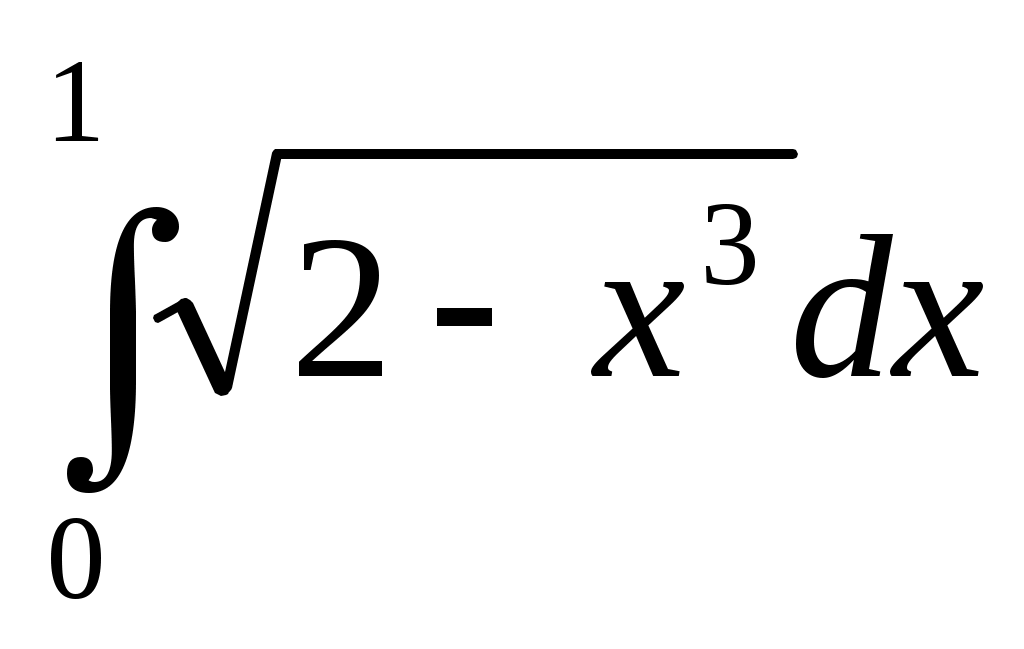 ;
;
254)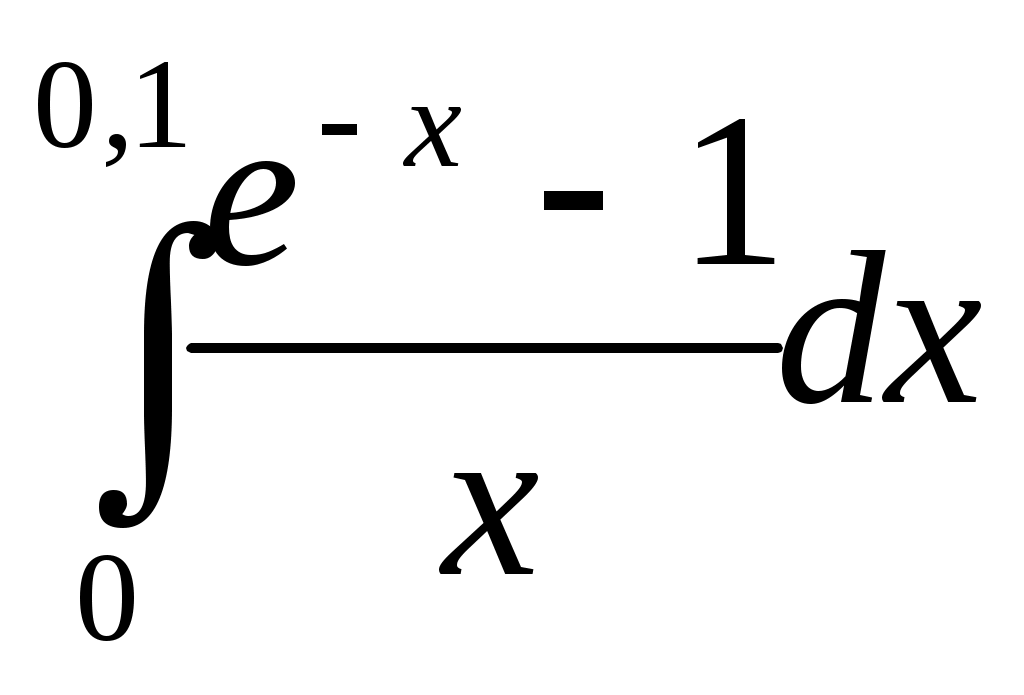 ;
;
355)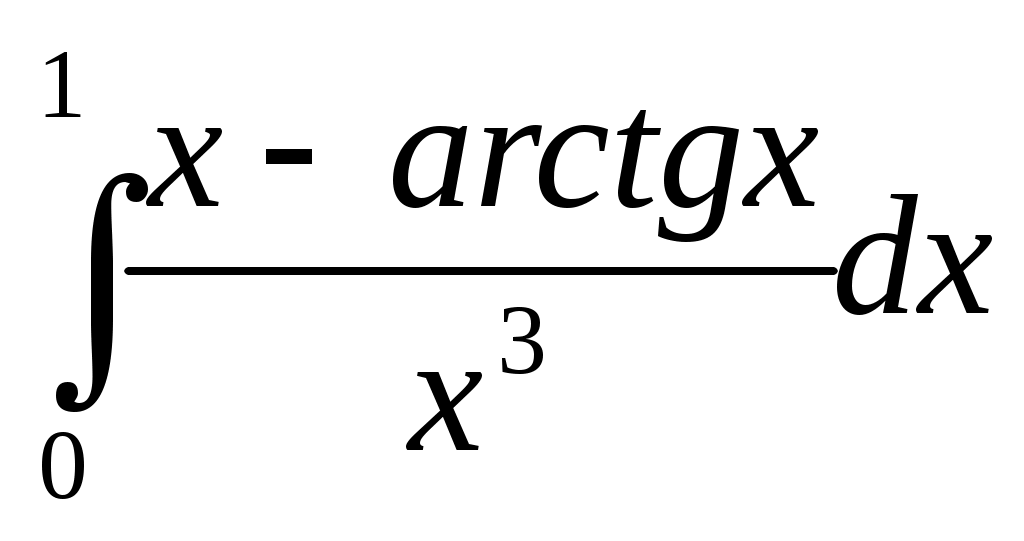 , δ=10-2;
, δ=10-2;
356)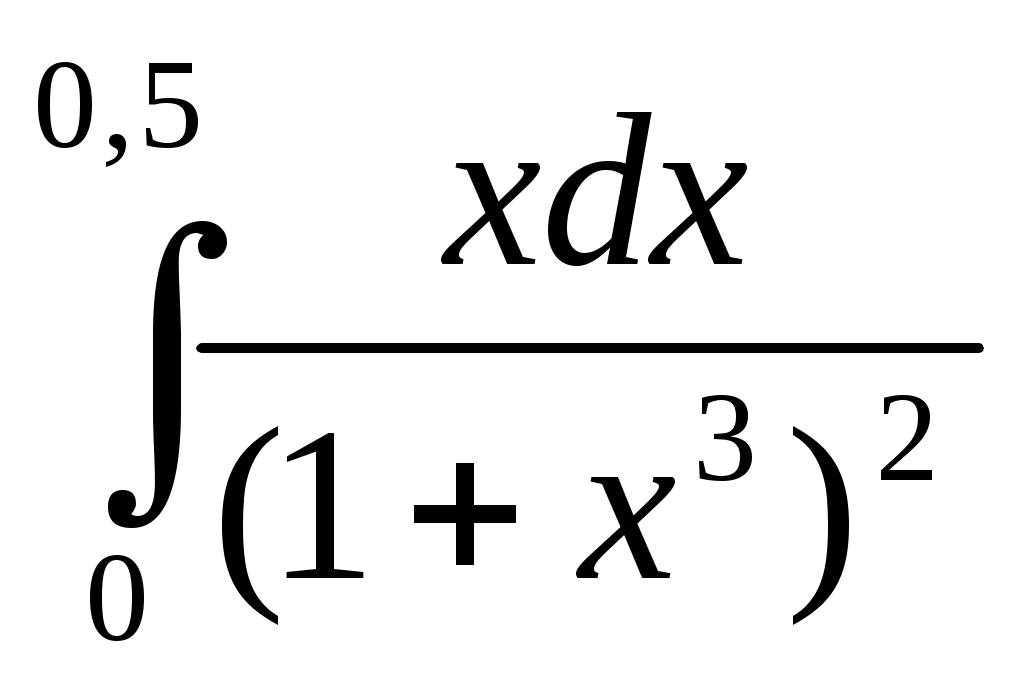 , δ=10-4;
, δ=10-4;
357)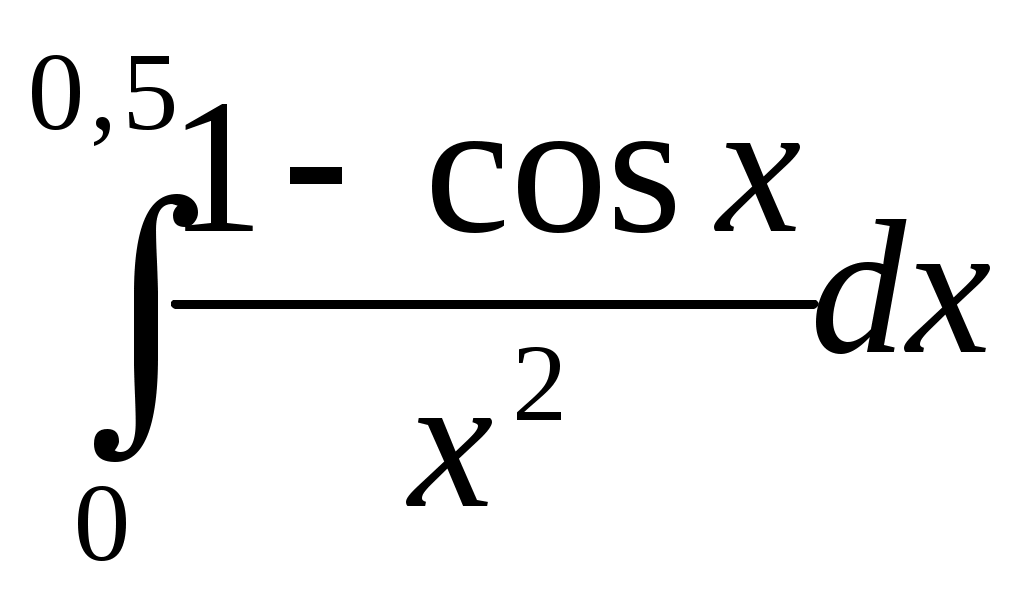 , δ=10-4;
, δ=10-4;
358)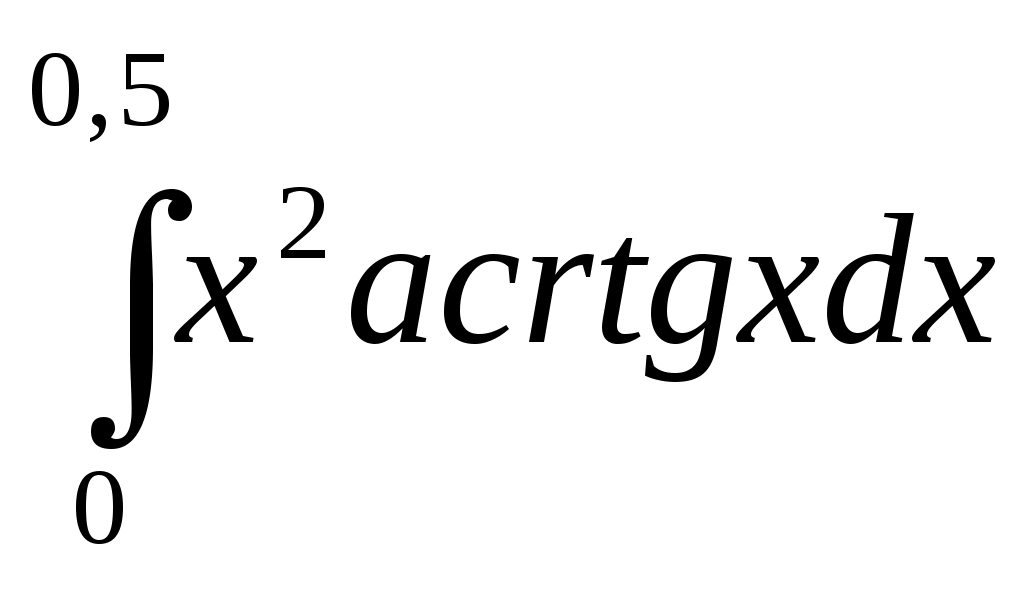 , δ=10-4;
, δ=10-4;
359)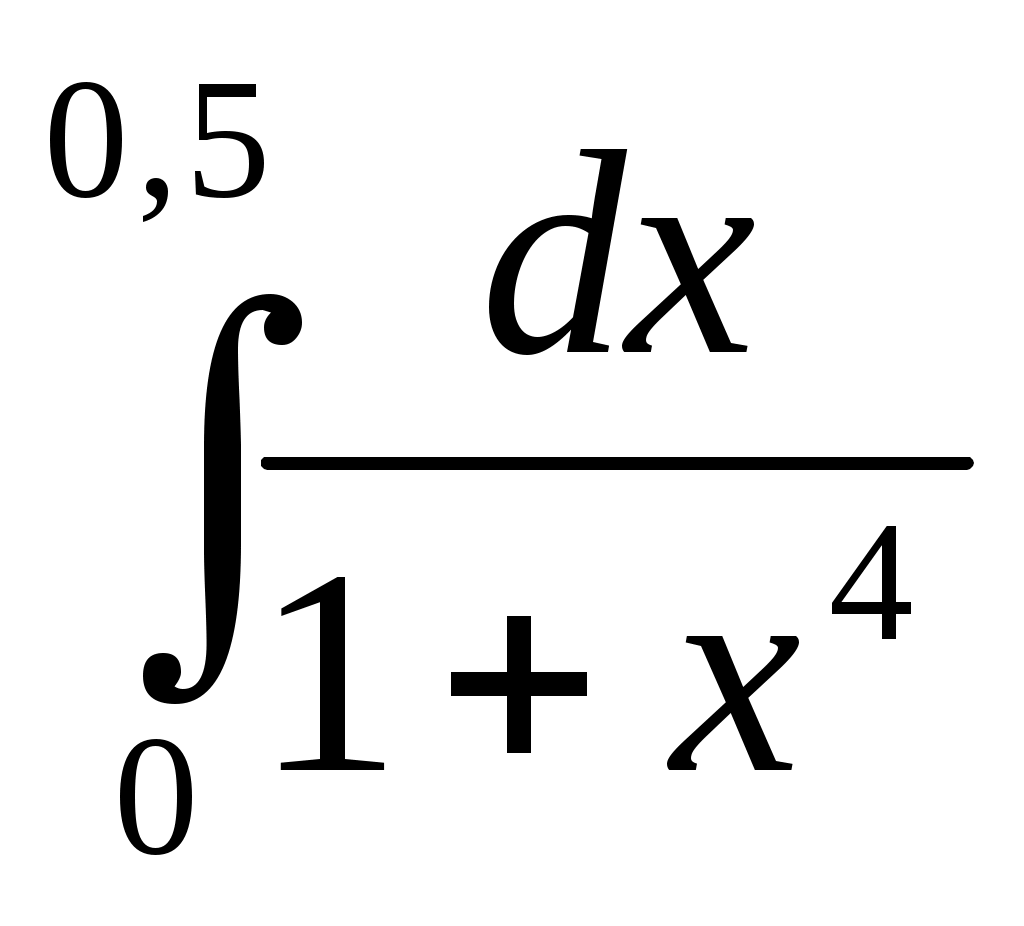 , δ=10-4.
, δ=10-4.
В задачах 260-279 найти пять первых членов разложения в степенной ряд частного решения дифференциального уравнения при заданных начальных условиях:
260)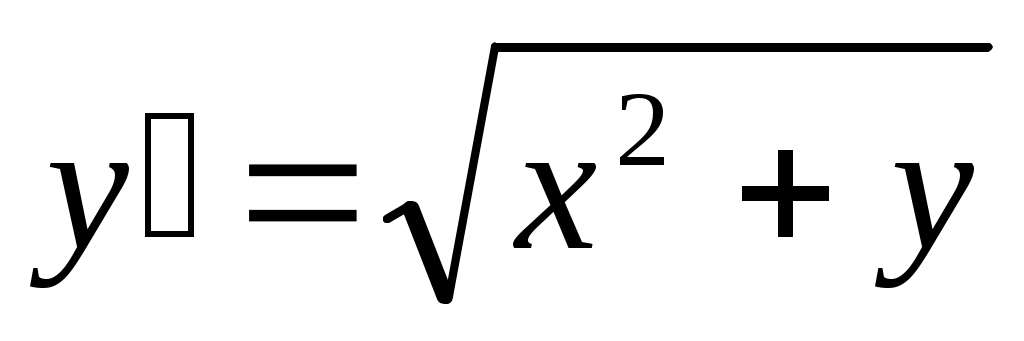 ; y(0)=1.
; y(0)=1.
261)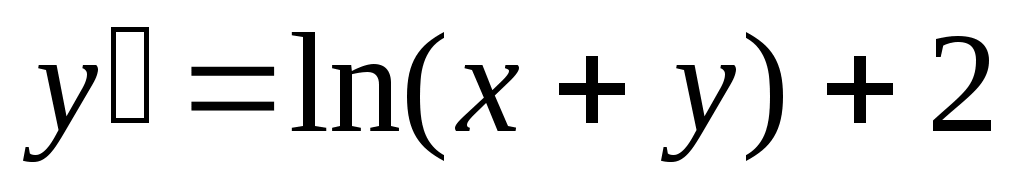 ; y(0)=1.
; y(0)=1.
262)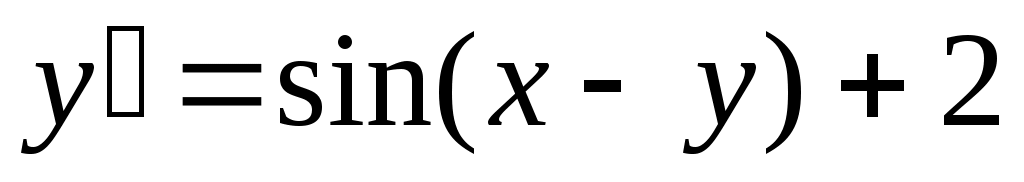 ; y(0)=1.
; y(0)=1.
263)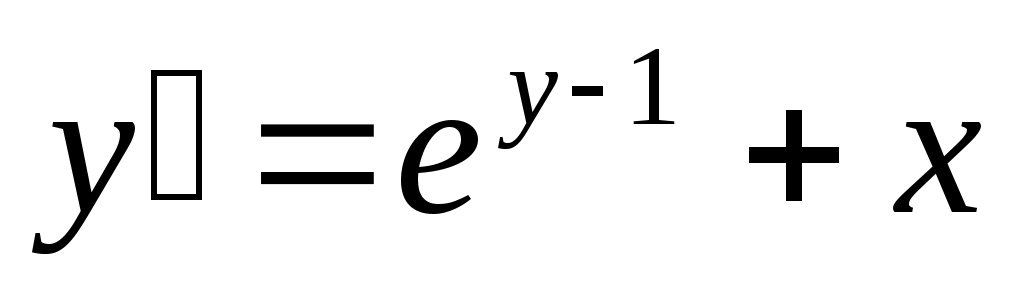 ; y(0)=1.
; y(0)=1.
264)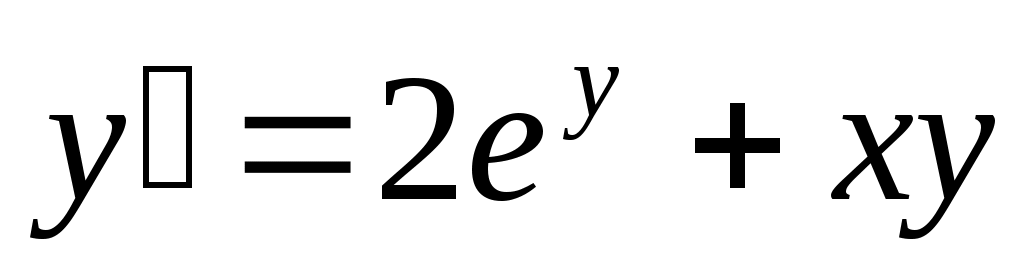 ; y(0)=0.
; y(0)=0.
265)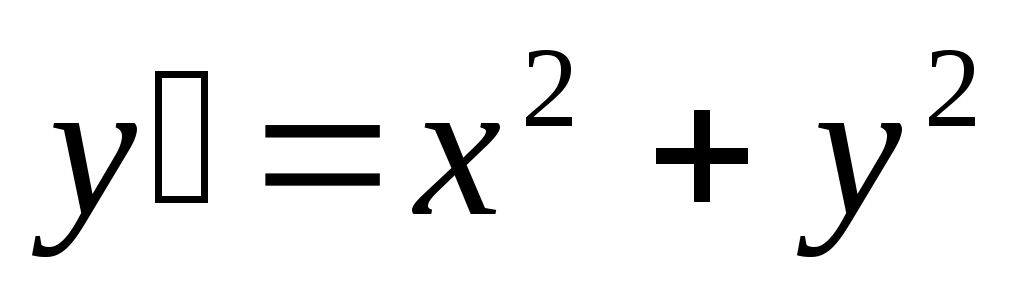 ; y(0)=2.
; y(0)=2.
266)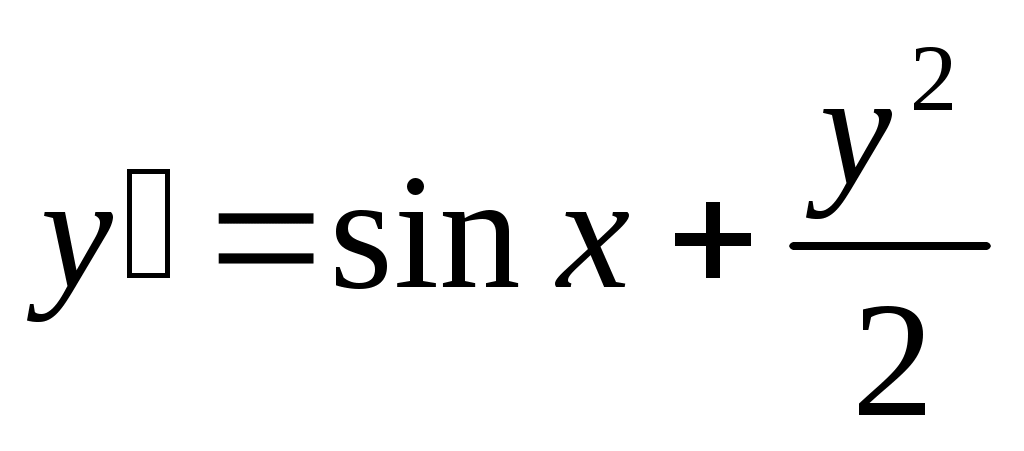 ; y(0)=1.
; y(0)=1.
267)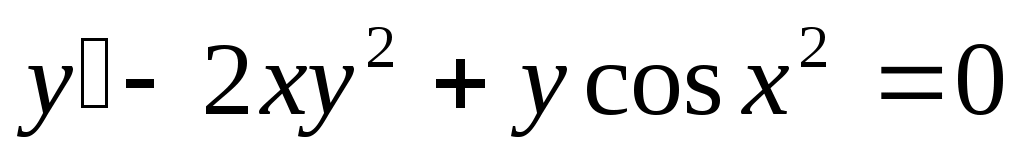 ; y(0)=1.
; y(0)=1.
268)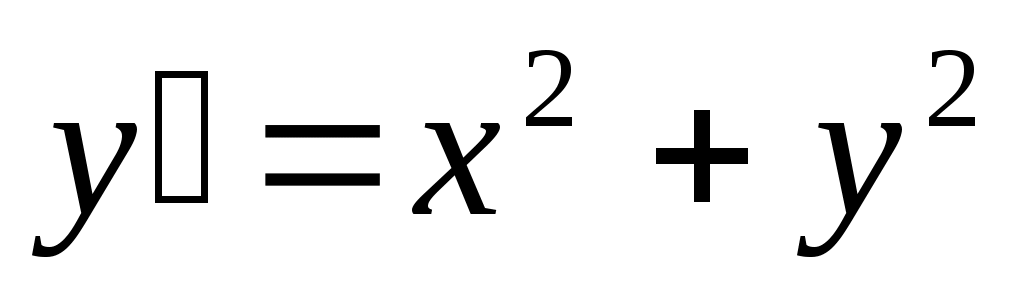 ; y(0)=1.
; y(0)=1.
269)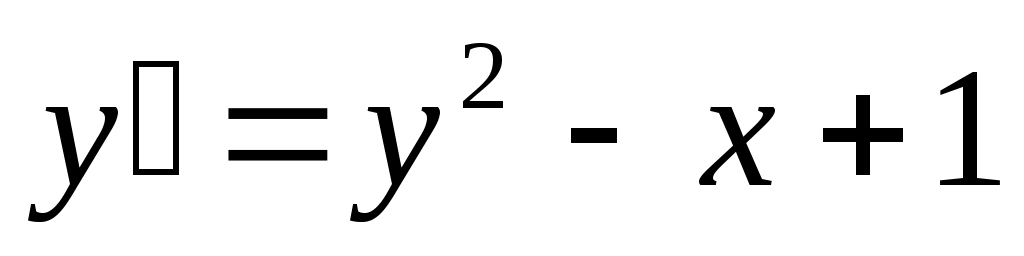 ; y(0)=1.
; y(0)=1.
270)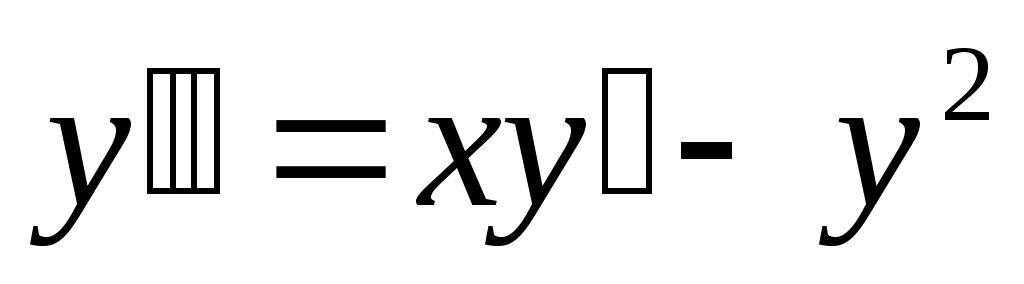 ; y(0)=1, y’(0)=2.
; y(0)=1, y’(0)=2.
271)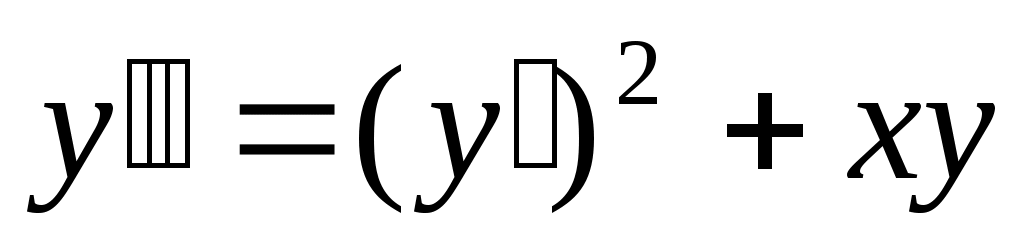 ; y(0)=4, y’(0)=2.
; y(0)=4, y’(0)=2.
272)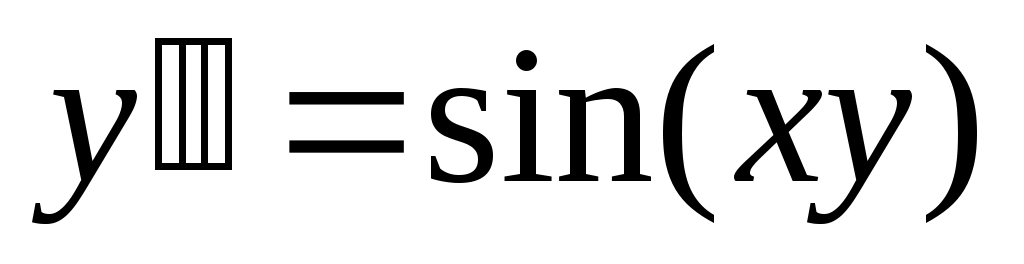
; y(0)=1, y’(0)=1.
273)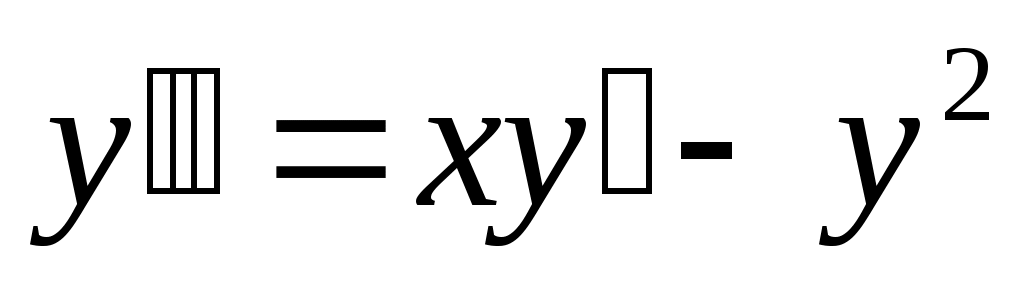 ; y(0)=1, y’(0)=1.
; y(0)=1, y’(0)=1.
274)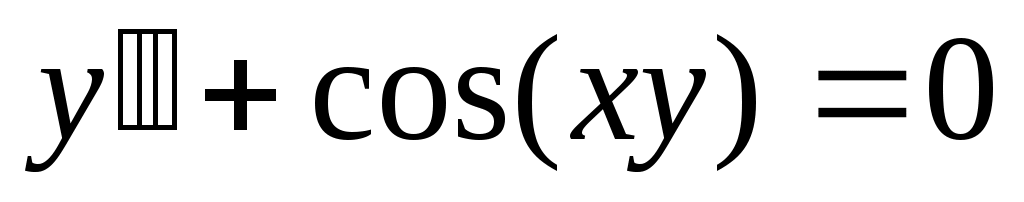 ; y(0)=а, y’(0)=0.
; y(0)=а, y’(0)=0.
275)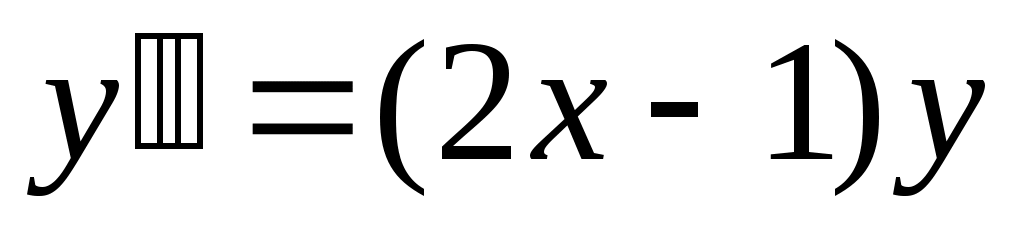 ; y(0)=0, y’(0)=1.
; y(0)=0, y’(0)=1.
276)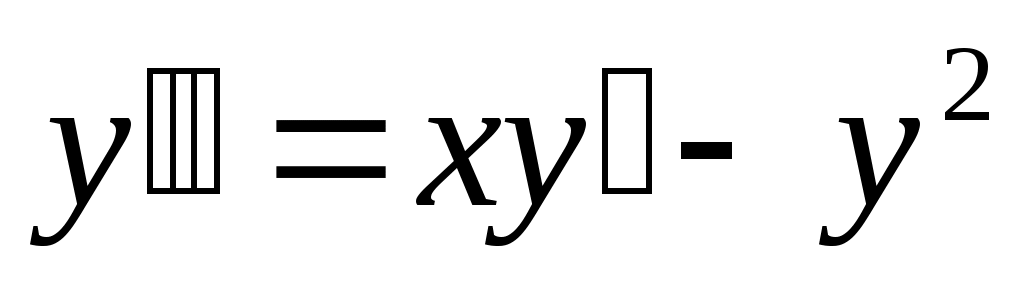 ; y(0)=2, y’(0)=2.
; y(0)=2, y’(0)=2.
277)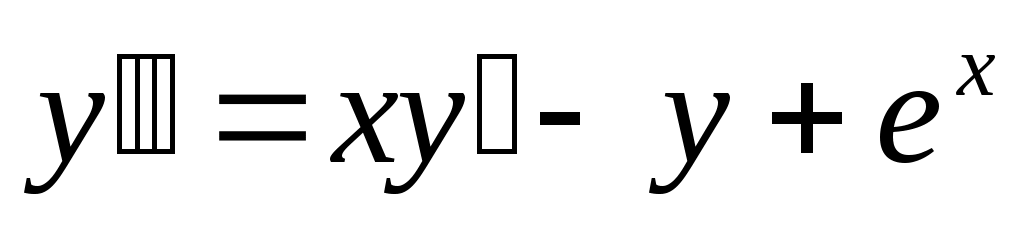 ; y(0)=0, y’(0)=1.
; y(0)=0, y’(0)=1.
278)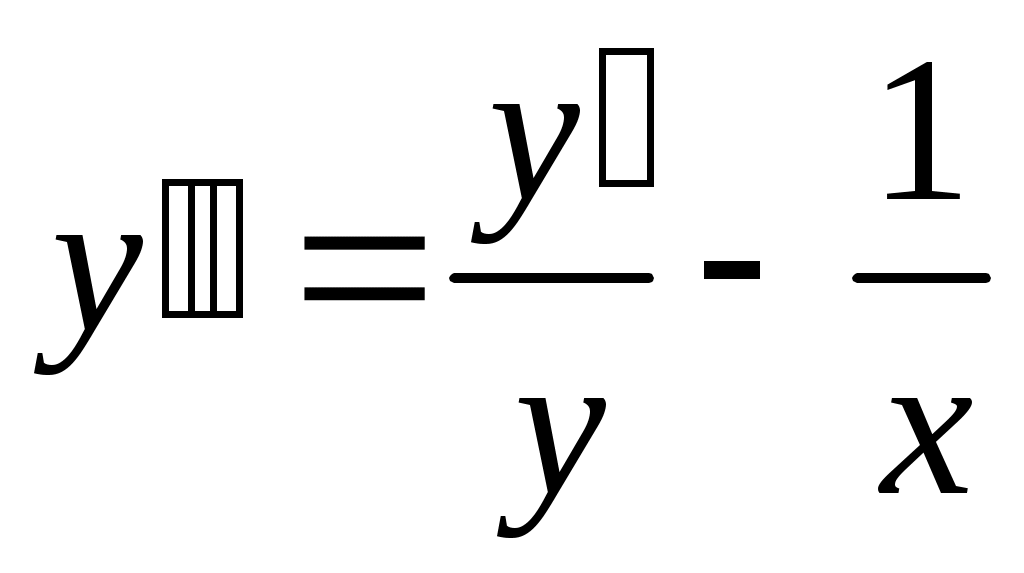 ; y(0)=1, y’(0)=0.
; y(0)=1, y’(0)=0.
279)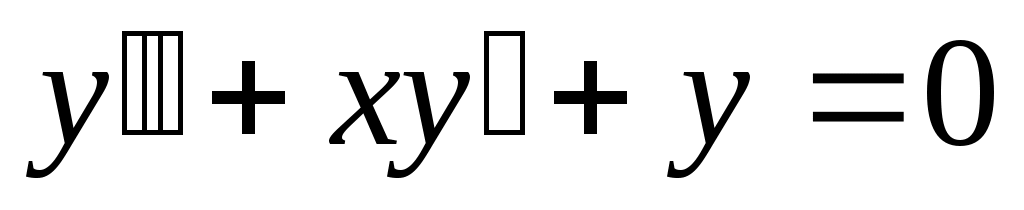 ; y(0)=1, y’(0)=1.
; y(0)=1, y’(0)=1.
В задачах 280-287 методом неопределенных коэффициентов найти пять первых членов разложения в степенной ряд частного решения дифференциального уравнения:
280)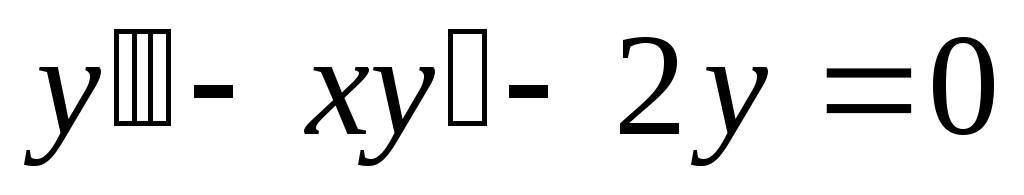 ; y(0)=0, y’(0)=1.
; y(0)=0, y’(0)=1.
281)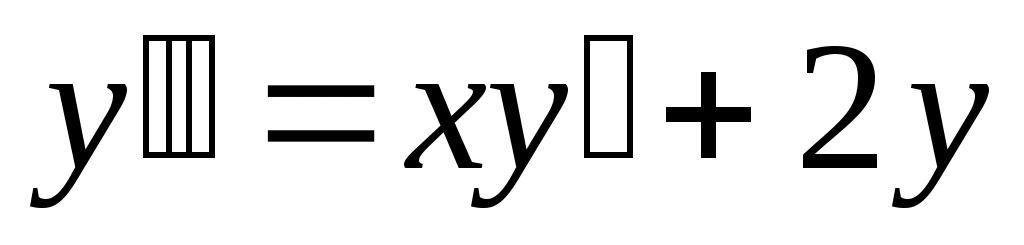 ; y(0)=0, y’(0)=1.
; y(0)=0, y’(0)=1.
282)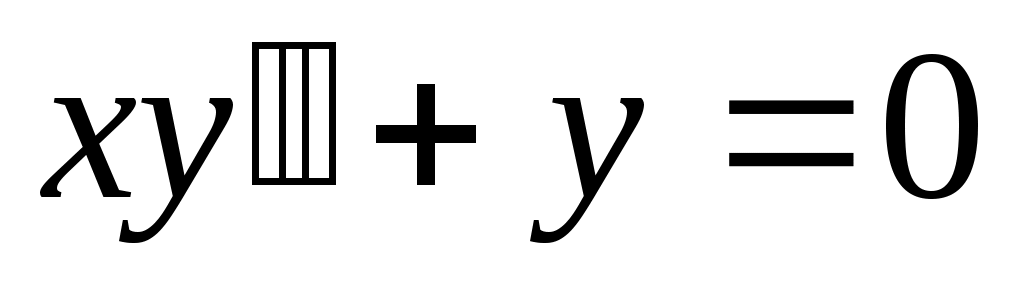 ; y(0)=0, y’(0)=1.
; y(0)=0, y’(0)=1.
283)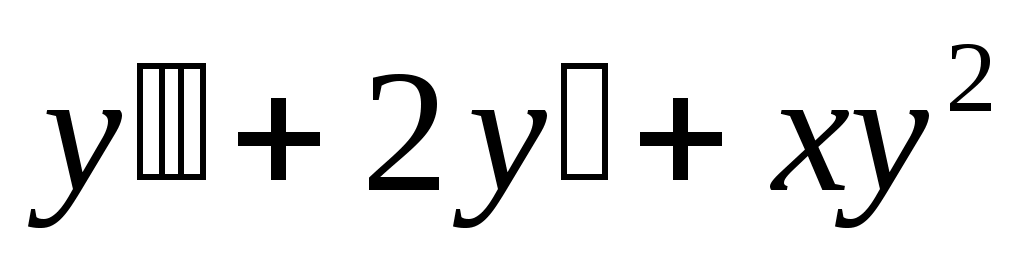 ; y(0)=1, y’(0)=0.
; y(0)=1, y’(0)=0.
284)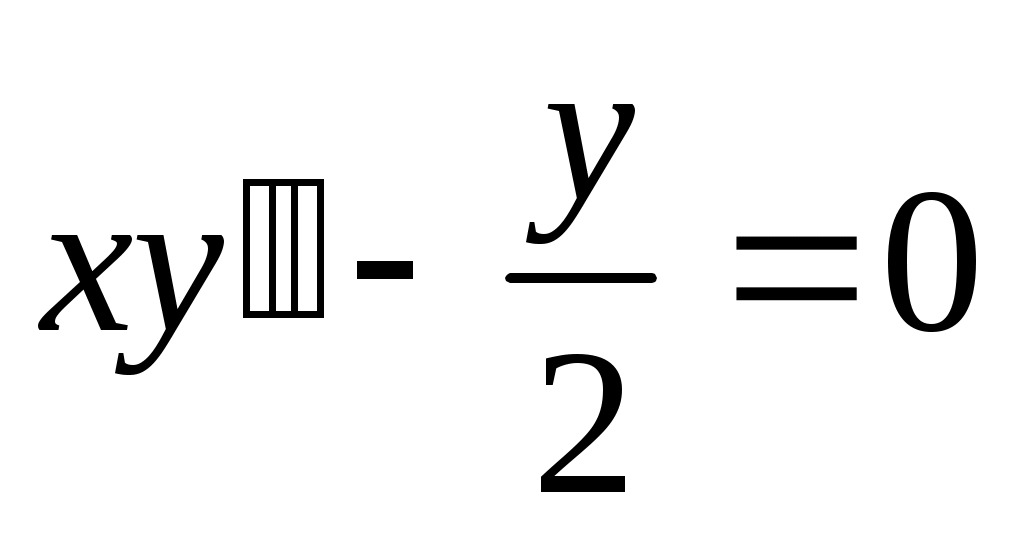 ; y(0)=0, y’(0)=1.
; y(0)=0, y’(0)=1.
285)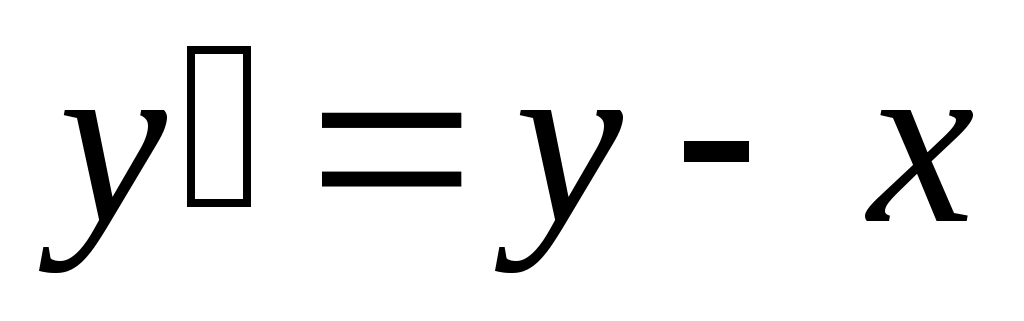 ; y(0)=1.
; y(0)=1.
286)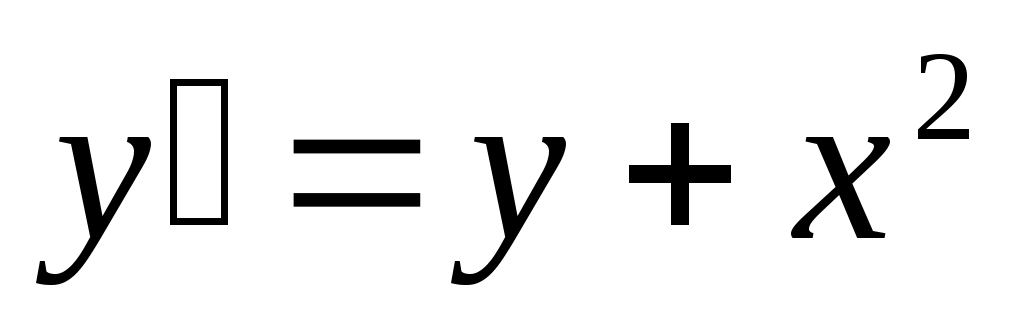 ; y(0)=-2.
; y(0)=-2.
§6. Ряды Фурье.
Пусть функция f(x) является периодической с периодом T=2l
Определение. Функциональный ряд вида
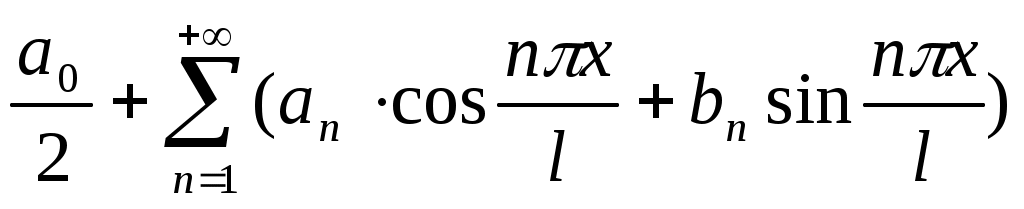 ,
,
где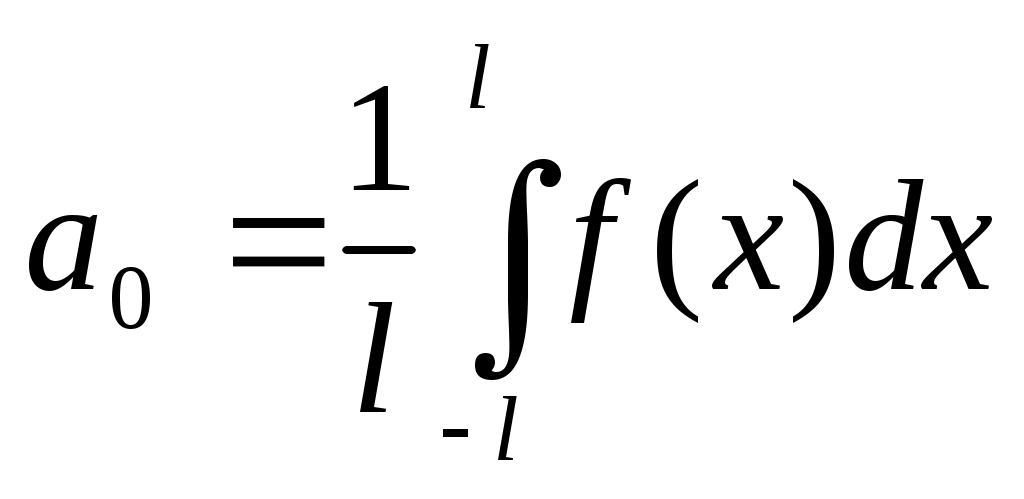 ;
; 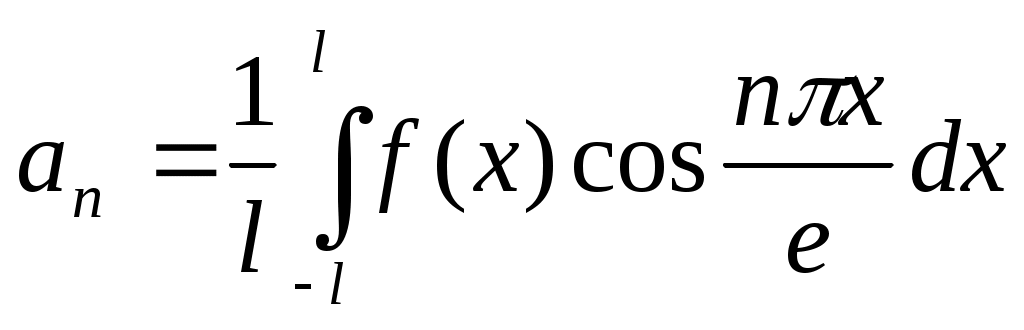 ;
;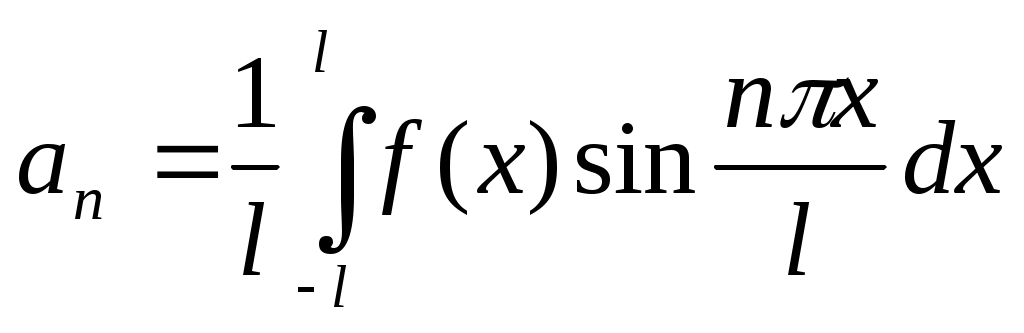 ; n=1,2...
; n=1,2...
называется рядом Фурье для функции f(x) в интервале [-l;l] .
Определение. Функция f(x) называется кусочно-гладкой в интервале (a;b), если она имеет на этом интервале лишь конечное число точек разрыва 1-го рода; в этих точках функция имеет предельные значения слева и справа: f(x-0) и f(x+0).
Основная теорема о возможности разложения функции f(x) в ряд Фурье формулируется следующим образом:
Теорема (Условия Дирихле) Если функция f(x) кусочно-гладкая в интервале [-l;l], то ее ряд Фурье сходится к функции f(x) во всех точках, в которых она непрерывна. В точках разрыва функции f(x) ряд сходится к среднему арифметическому ее предельных значений слева и справа, т.е. к значению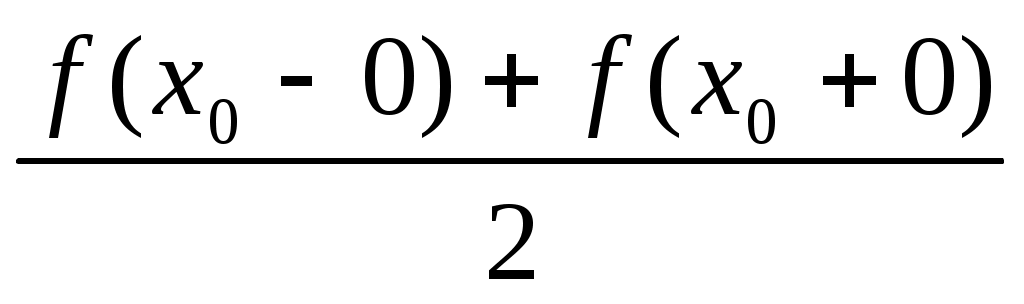 , где x0 – точка разрыва 1-го рода. В обеих граничных точках интервала сумма ряда равна среднему арифметическому предельных значений функции при стремлении независимой переменно к этим точкам изнутри интервала:
, где x0 – точка разрыва 1-го рода. В обеих граничных точках интервала сумма ряда равна среднему арифметическому предельных значений функции при стремлении независимой переменно к этим точкам изнутри интервала: 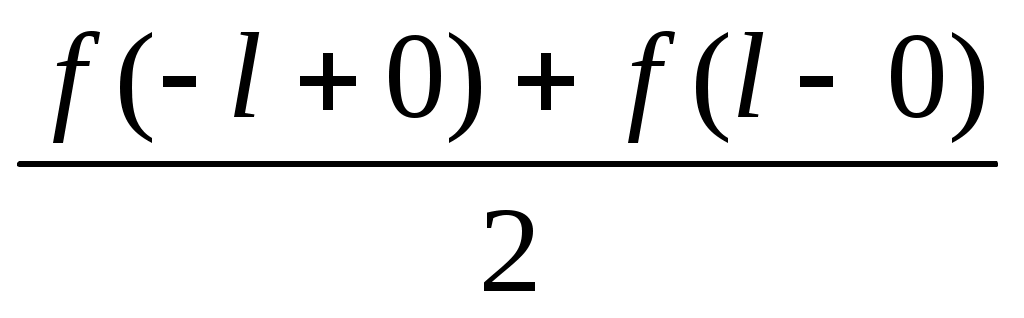 .
.
Условие кусочной гладкости слева и справа, т.е. у арифметическому ее точках разрыва функции ф(ч)дельные значения слева и справаения дифференциала:в теореме может быть заменено на условие непрерывности и существования конечного числа точек экстремума.
Если функция f(x) четна (f(-x)=f(x)), то все коэффициенты bn=0 и соответствующий ряд Фурье не содержит синусов:
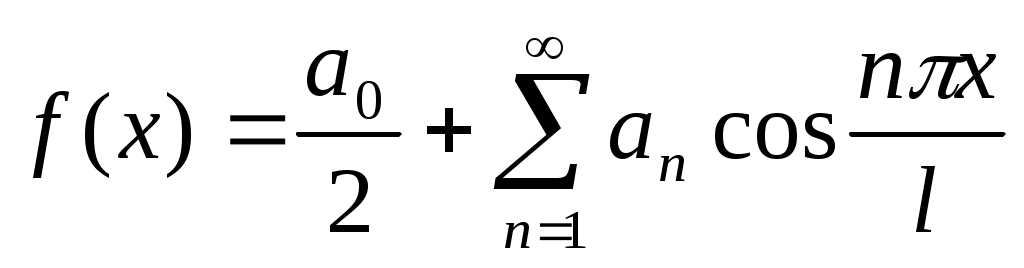 ;
; 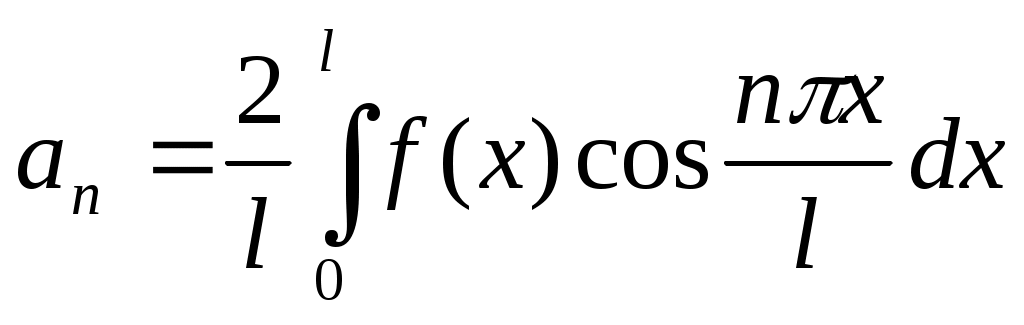 , n=1,2,....
, n=1,2,....
Для нечетной функции (f(-x)=-f(x)), то все коэффициенты bn=0 и соответствующий ряд Фурье содержит только синусы:
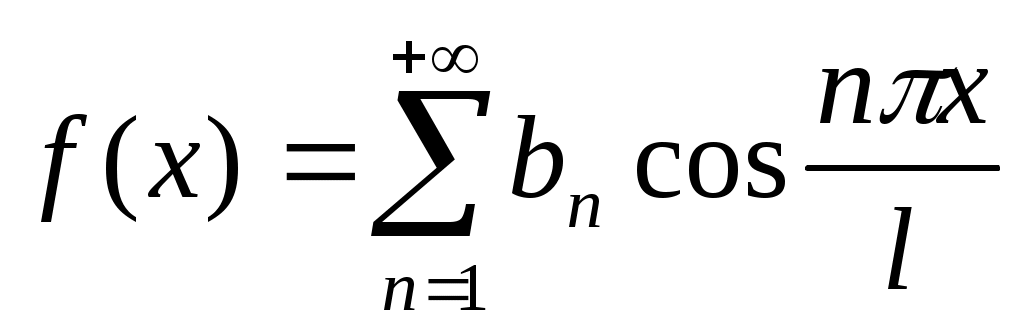 ;
; 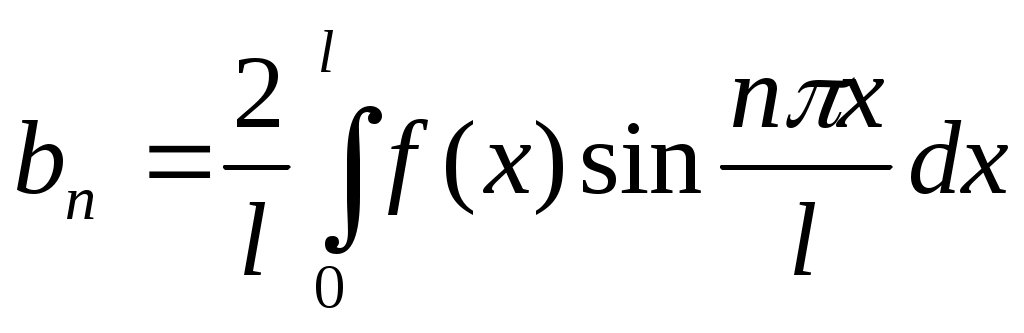 , n=1,2,....
, n=1,2,....
Функцию f(x), заданную в интервале [0;l], можно произвольно продолжить в соседний интервал [-l;0) и поэтому ее можно представить различными рядами Фурье. Пользуясь этим, такую функцию обычно представляют неполным рядом Фурье, содержащим только косинусы или только синусы.
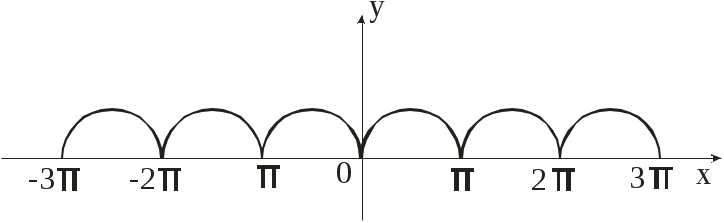
Р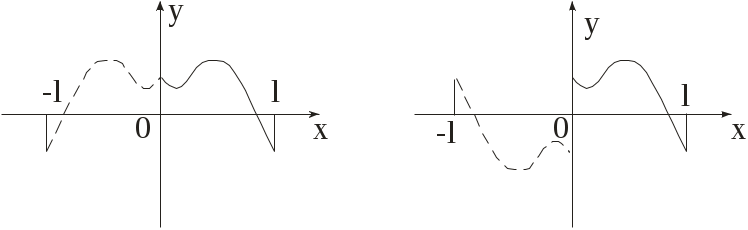 яд по косинусам получается при четном, а ряд по синусам при нечетном продолжении данной функции на соседней слева интервал [-l;0). В первом случае график данной функции продолжается на интервал [-l;0) симметрично относительно оси ординат, а во втором случае – симметрично относительно начала координат (см. рисунок).
яд по косинусам получается при четном, а ряд по синусам при нечетном продолжении данной функции на соседней слева интервал [-l;0). В первом случае график данной функции продолжается на интервал [-l;0) симметрично относительно оси ординат, а во втором случае – симметрично относительно начала координат (см. рисунок).
Пример. Разложить в ряд Фурье функции в указанном промежутке
1)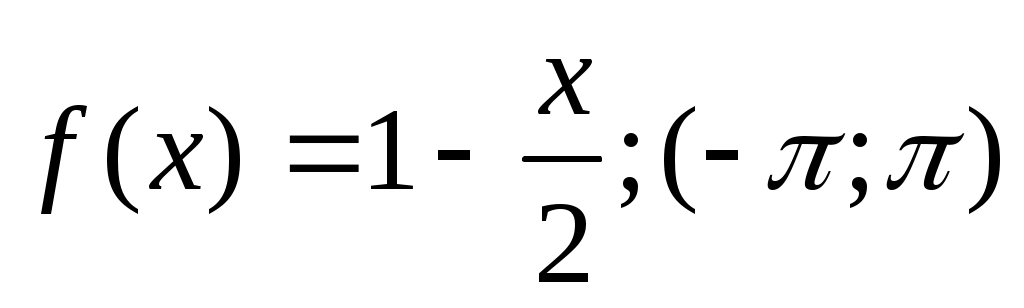 ;
;
2)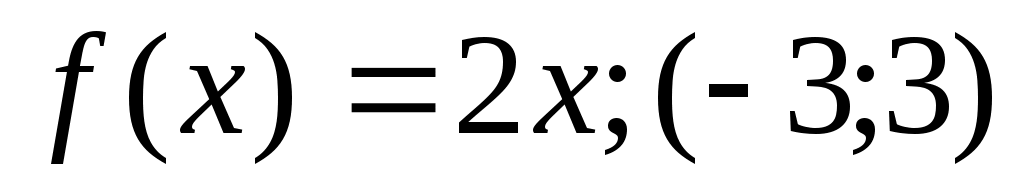 ;
;
3)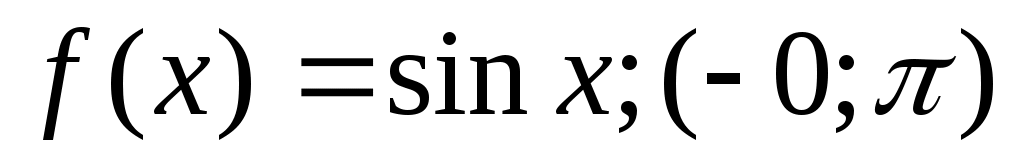 по косинусам.
по косинусам.
Решение:
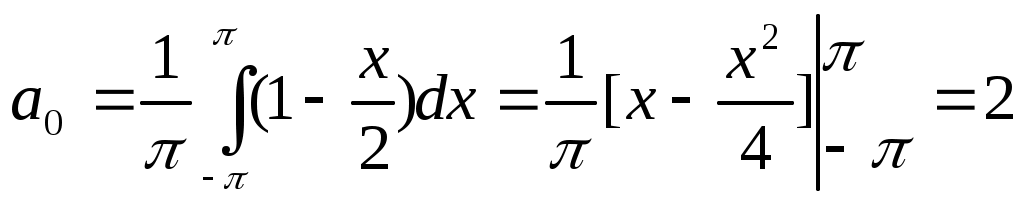
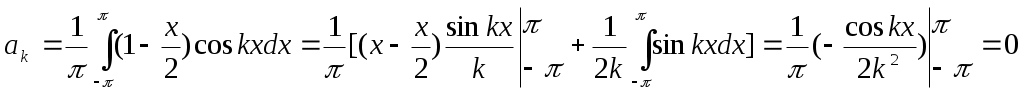
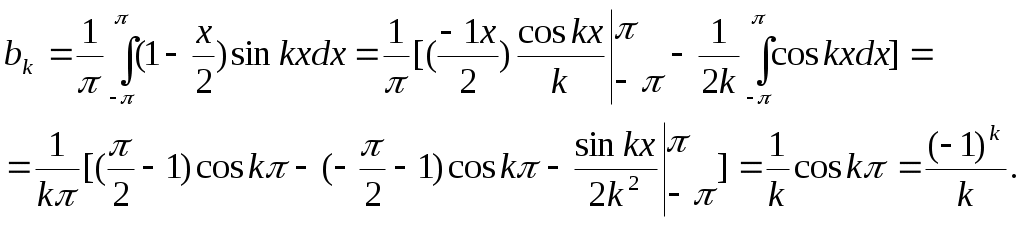
Представляя найденные значения коэффициентов в стандартный ряд, получаем разложения функции в ряд Фурье:
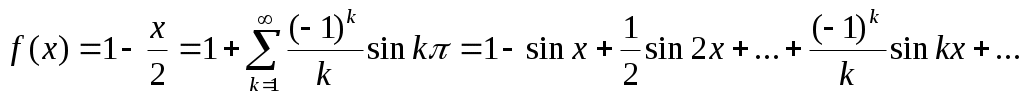
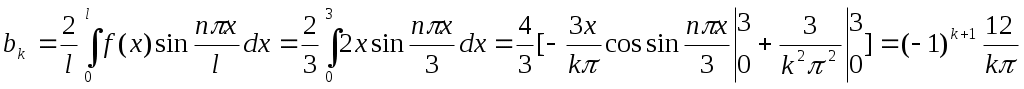 .
.
Следовательно,
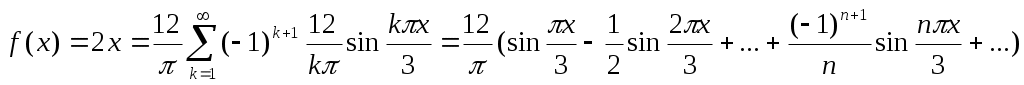 .
.
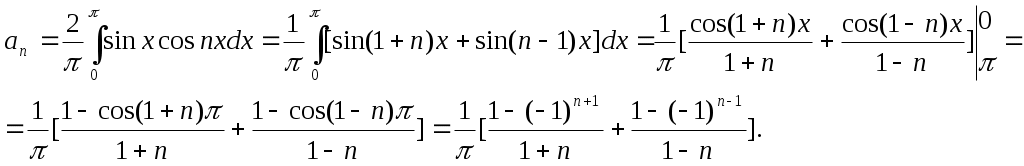
Следовательно,
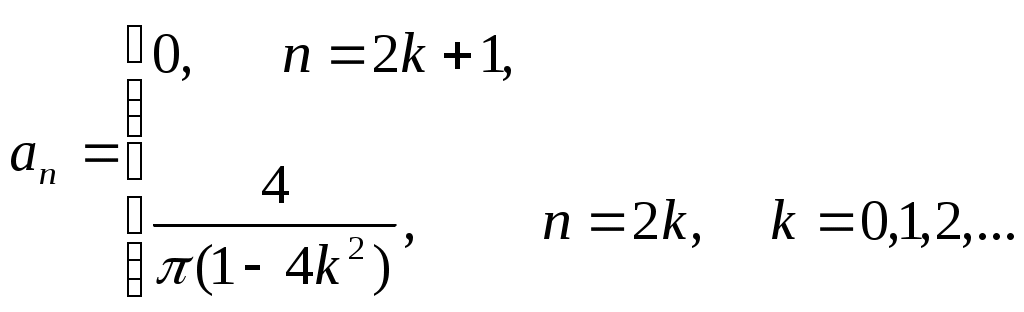
При n=1 полученное здесь общее выражение для an непригодно, вследствие чего коэффициент a1 вычисляется отдельно, полагая n=1 в общей формуле.
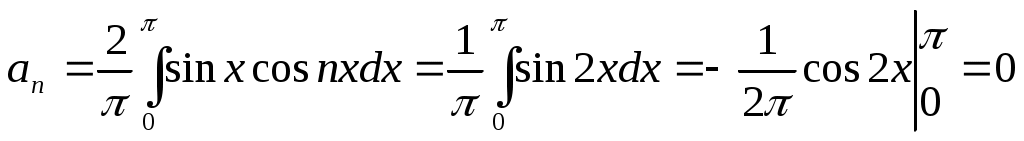 .
.
Представив значения коэффициентов в ряд, получим искомое разложение:
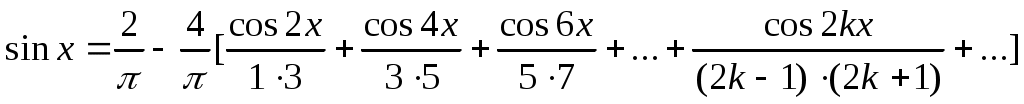
Задачи для решения
288)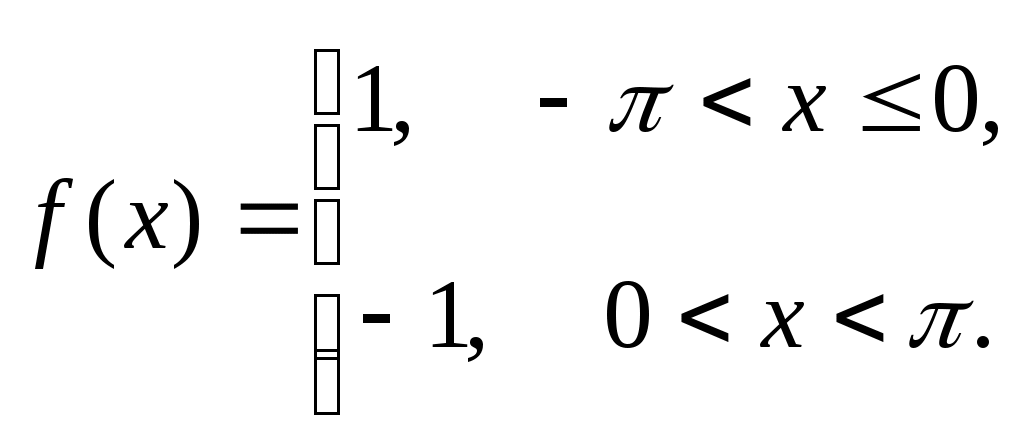
289)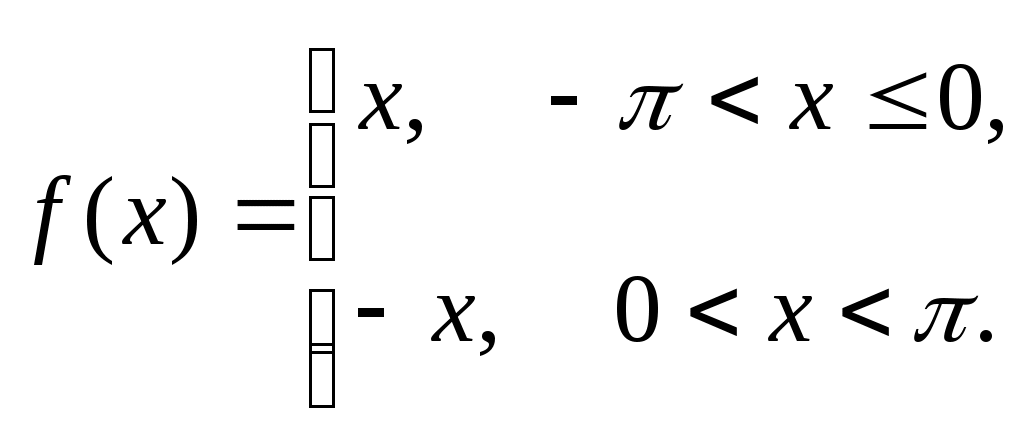
290)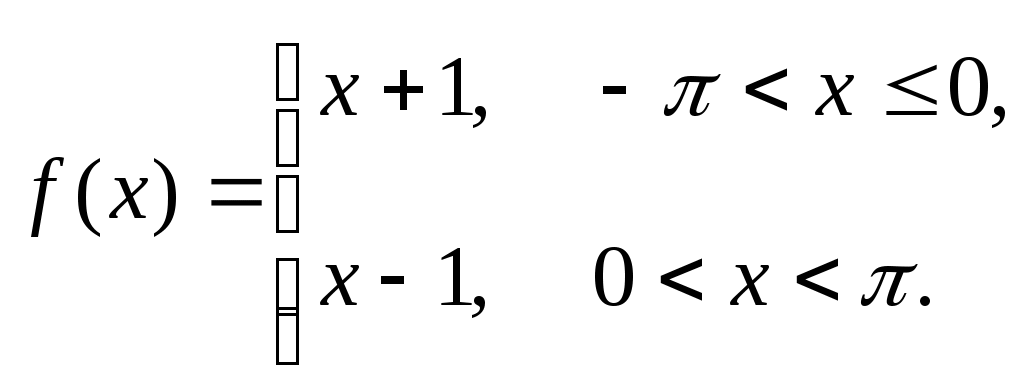
291)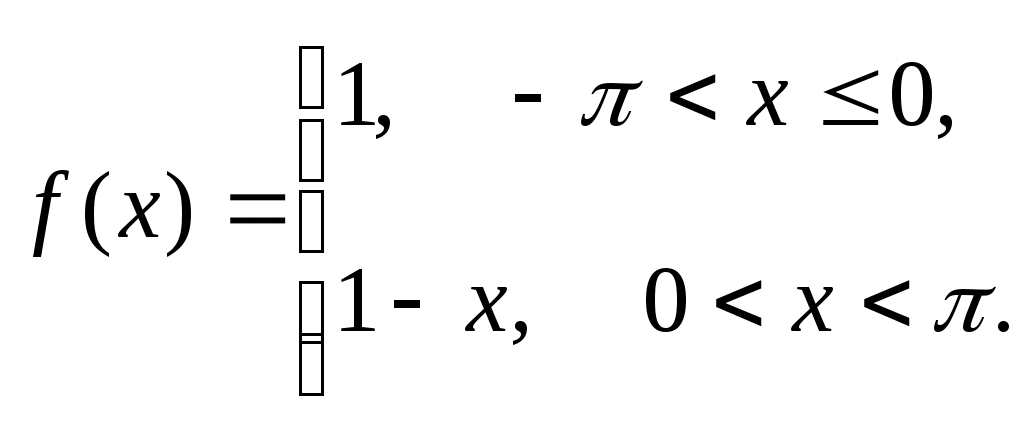
292)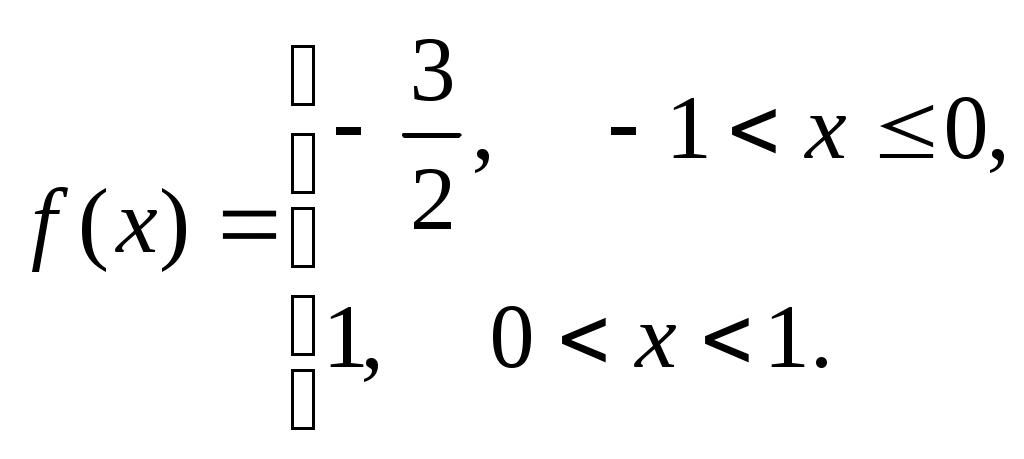
293)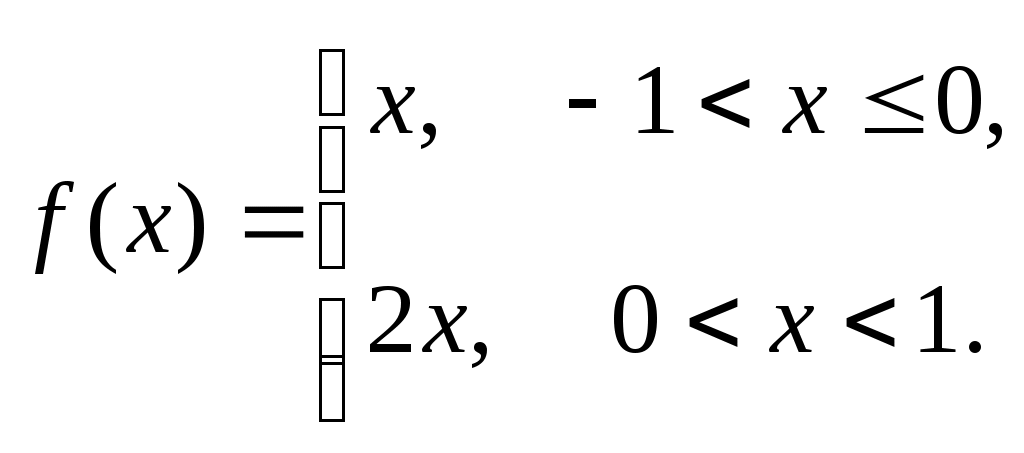
294)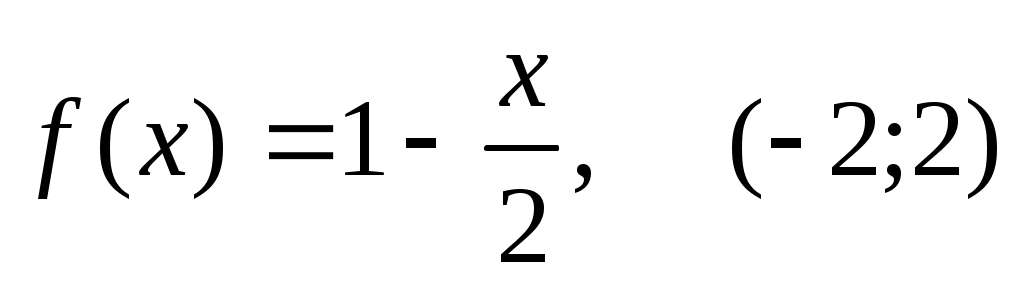 .
.
295)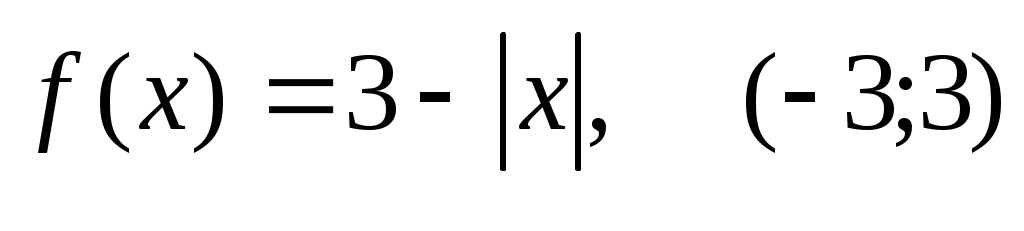 .
.
296)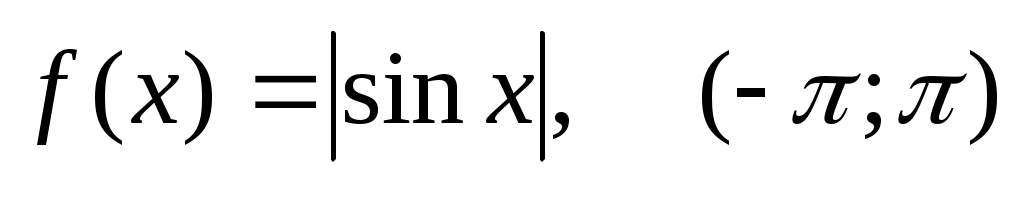 .
.
297)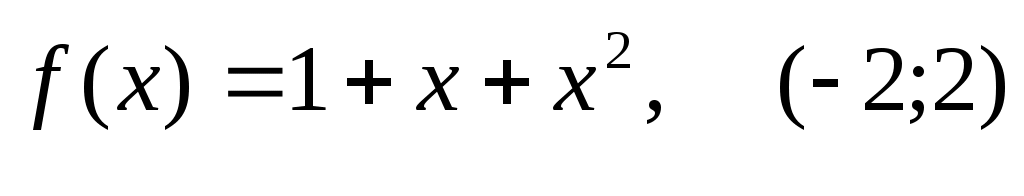 .
.
298)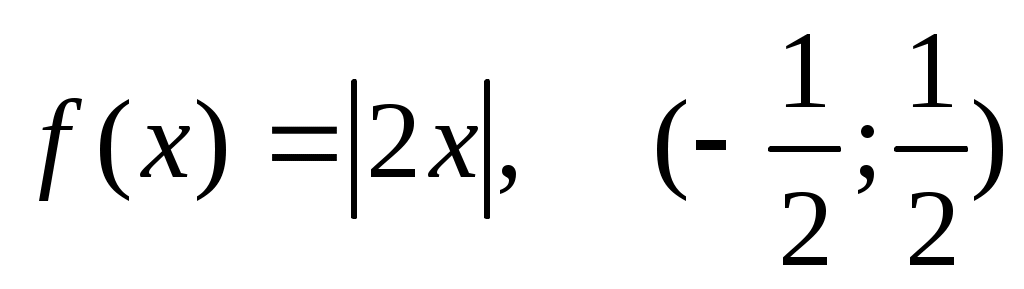 .
.
299)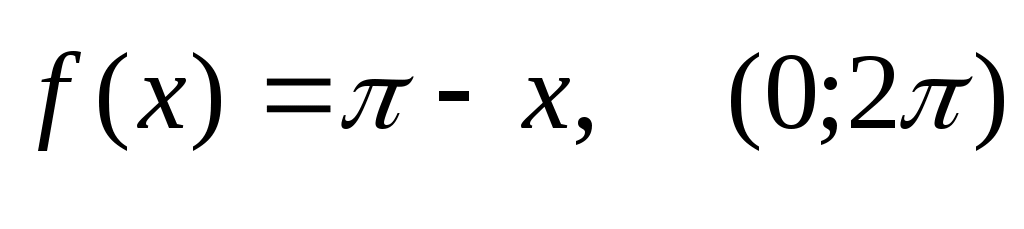
300)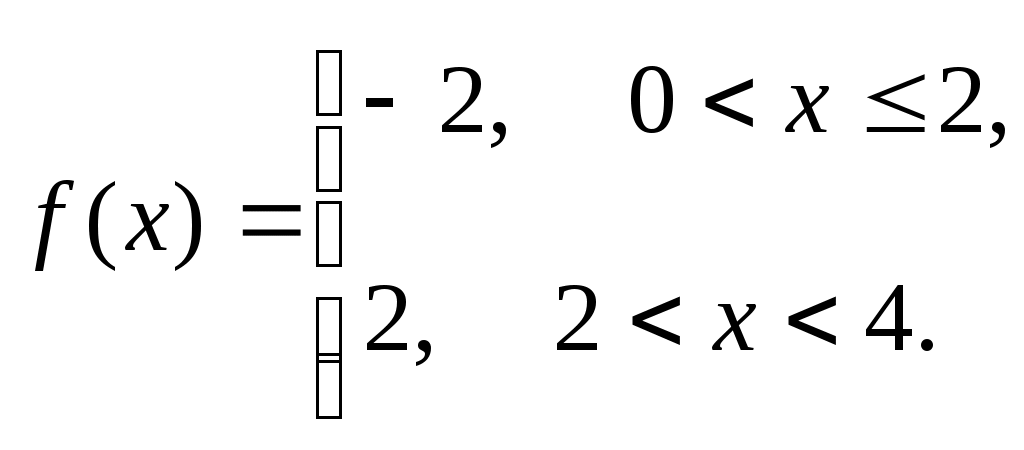
301)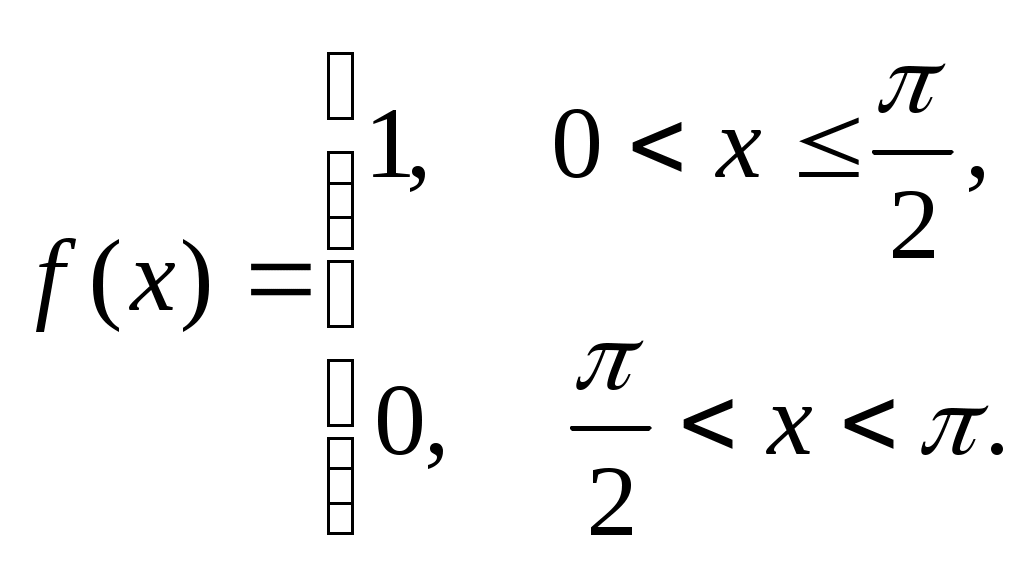 - по синусам.
- по синусам.
302)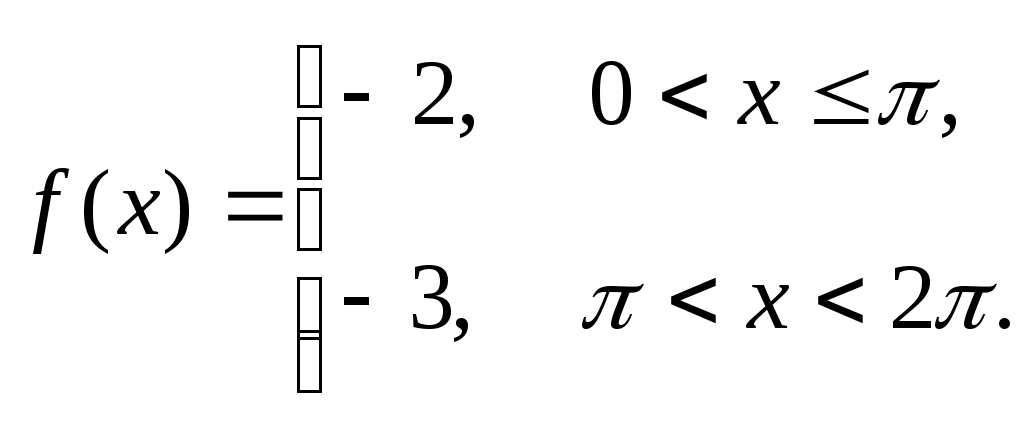
303)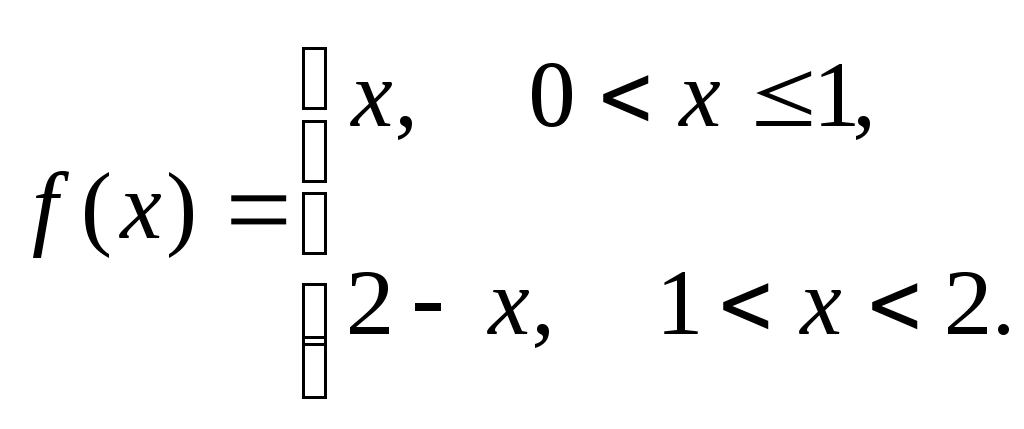 - по косинусам
- по косинусам
304)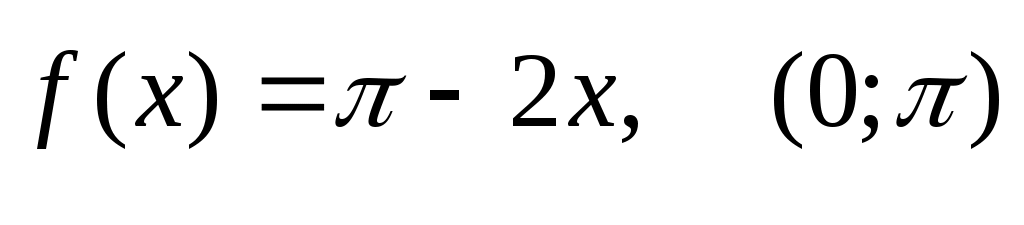 - по синусам.
- по синусам.
305)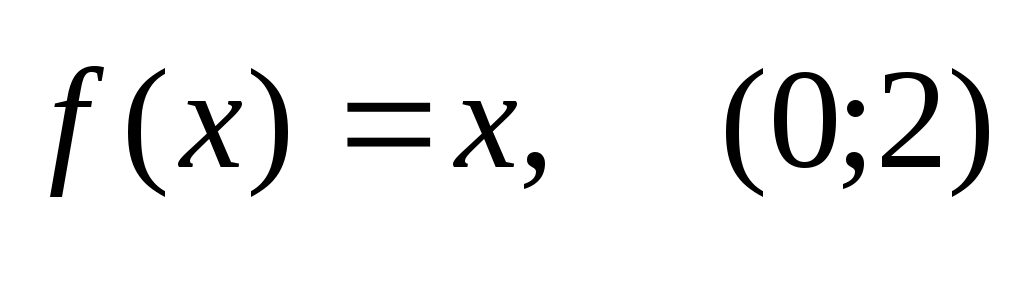 - по косинусам.
- по косинусам.
306)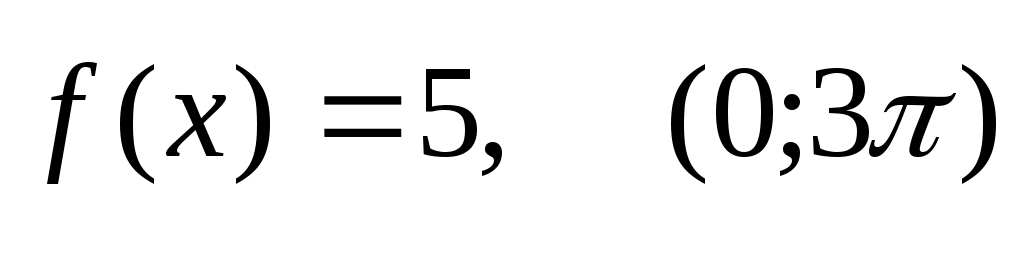 - по синусам.
- по синусам.
249)
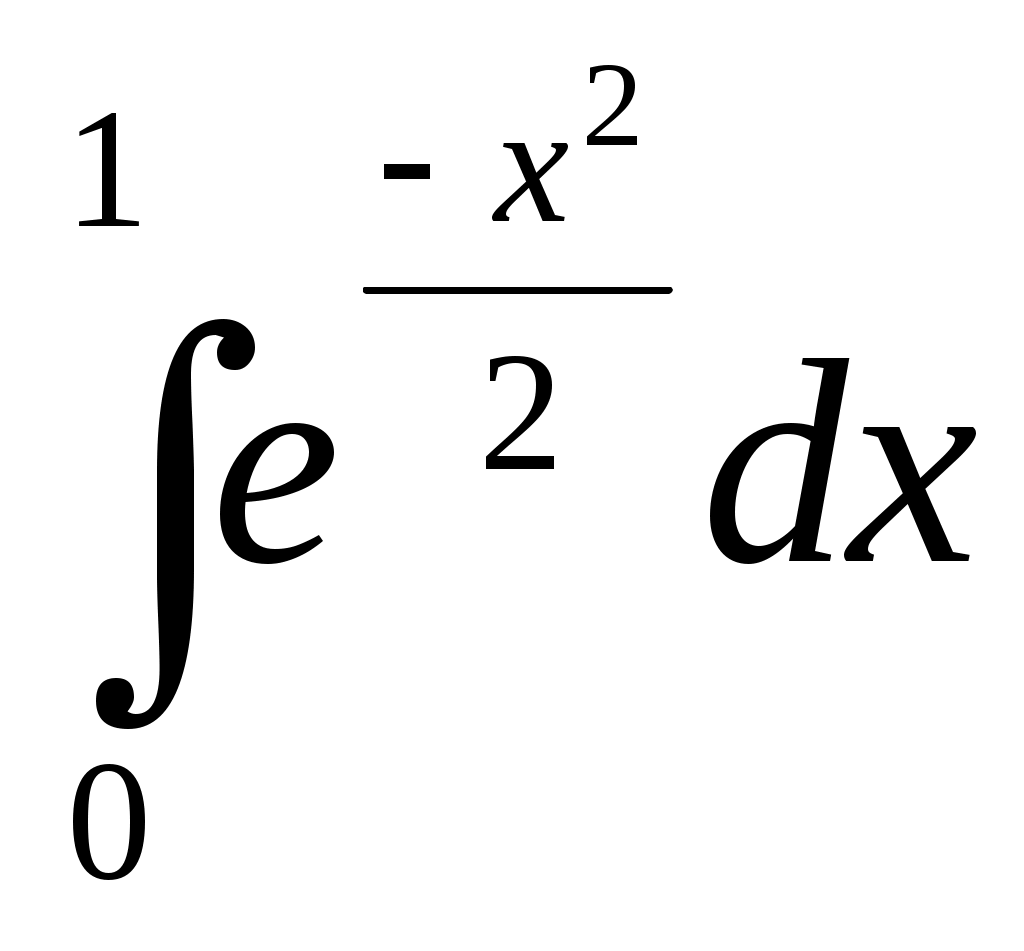 ;
;250)
251)
252)
253)
254)
355)
356)
357)
358)
359)
В задачах 260-279 найти пять первых членов разложения в степенной ряд частного решения дифференциального уравнения при заданных начальных условиях:
260)
261)
262)
263)
264)
265)
266)
267)
268)
269)
270)
271)
272)
; y(0)=1, y’(0)=1.
273)
274)
275)
276)
277)
278)
279)
В задачах 280-287 методом неопределенных коэффициентов найти пять первых членов разложения в степенной ряд частного решения дифференциального уравнения:
280)
281)
282)
283)
284)
285)
286)
§6. Ряды Фурье.
Пусть функция f(x) является периодической с периодом T=2l
Определение. Функциональный ряд вида
где
называется рядом Фурье для функции f(x) в интервале [-l;l] .
Определение. Функция f(x) называется кусочно-гладкой в интервале (a;b), если она имеет на этом интервале лишь конечное число точек разрыва 1-го рода; в этих точках функция имеет предельные значения слева и справа: f(x-0) и f(x+0).
Основная теорема о возможности разложения функции f(x) в ряд Фурье формулируется следующим образом:
Теорема (Условия Дирихле) Если функция f(x) кусочно-гладкая в интервале [-l;l], то ее ряд Фурье сходится к функции f(x) во всех точках, в которых она непрерывна. В точках разрыва функции f(x) ряд сходится к среднему арифметическому ее предельных значений слева и справа, т.е. к значению
Условие кусочной гладкости слева и справа, т.е. у арифметическому ее точках разрыва функции ф(ч)дельные значения слева и справаения дифференциала:в теореме может быть заменено на условие непрерывности и существования конечного числа точек экстремума.
Если функция f(x) четна (f(-x)=f(x)), то все коэффициенты bn=0 и соответствующий ряд Фурье не содержит синусов:
Для нечетной функции (f(-x)=-f(x)), то все коэффициенты bn=0 и соответствующий ряд Фурье содержит только синусы:
Функцию f(x), заданную в интервале [0;l], можно произвольно продолжить в соседний интервал [-l;0) и поэтому ее можно представить различными рядами Фурье. Пользуясь этим, такую функцию обычно представляют неполным рядом Фурье, содержащим только косинусы или только синусы.
Р
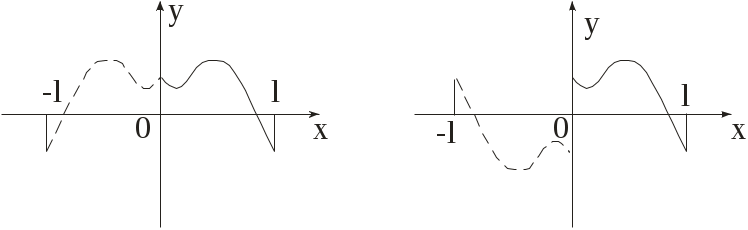 яд по косинусам получается при четном, а ряд по синусам при нечетном продолжении данной функции на соседней слева интервал [-l;0). В первом случае график данной функции продолжается на интервал [-l;0) симметрично относительно оси ординат, а во втором случае – симметрично относительно начала координат (см. рисунок).
яд по косинусам получается при четном, а ряд по синусам при нечетном продолжении данной функции на соседней слева интервал [-l;0). В первом случае график данной функции продолжается на интервал [-l;0) симметрично относительно оси ординат, а во втором случае – симметрично относительно начала координат (см. рисунок).Пример. Разложить в ряд Фурье функции в указанном промежутке
1)
2)
3)
Решение:
-
Используем общие формулы для ряда Фурье; l=π.
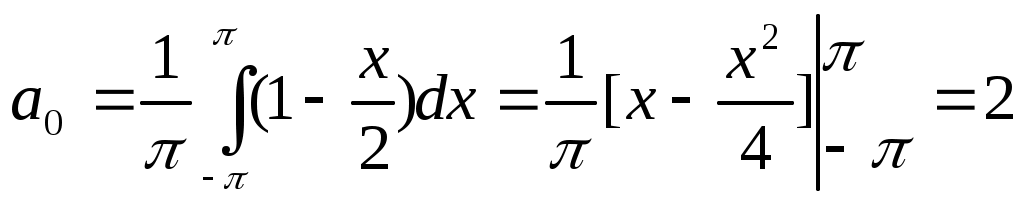
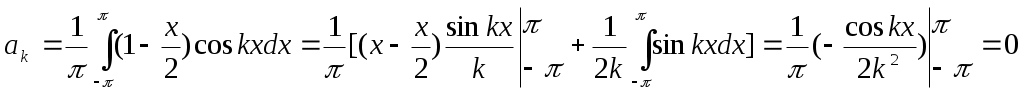
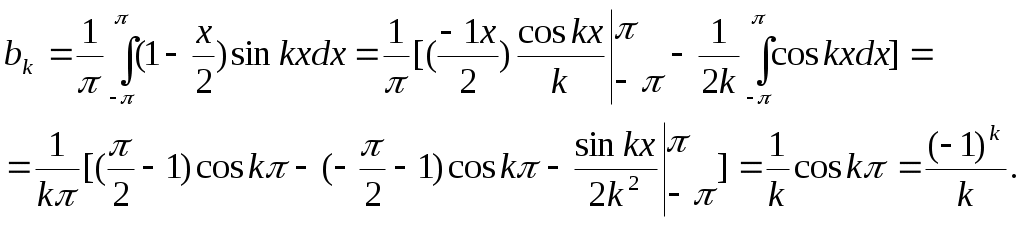
Представляя найденные значения коэффициентов в стандартный ряд, получаем разложения функции в ряд Фурье:

-
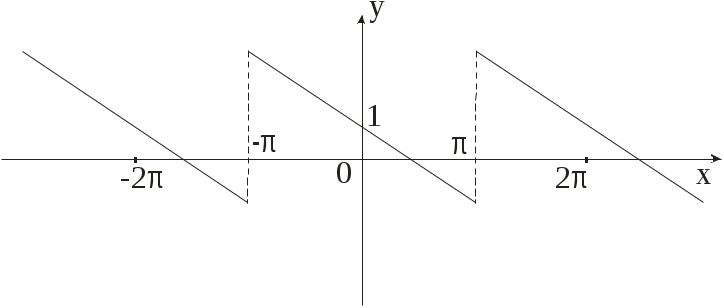
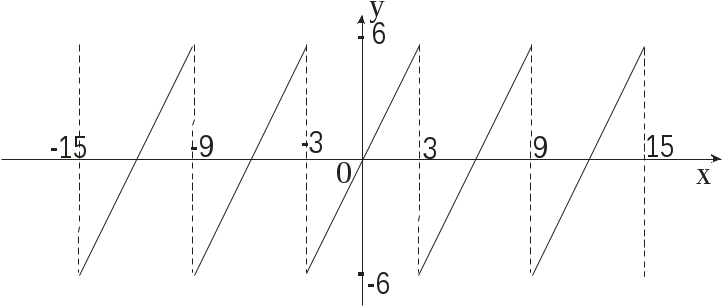
Функция f(x)=2x является нечетной, поэтому разлагается в ряд по синусам: a0=0, ak=0; (l=3)
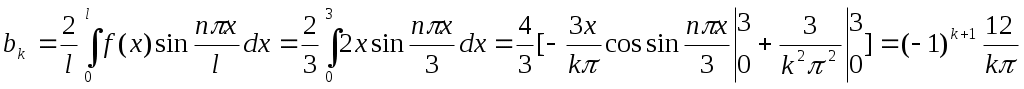 .
.Следовательно,

-
Данная функция четная, в следствии чего коэффициенты bn=0, l=π.
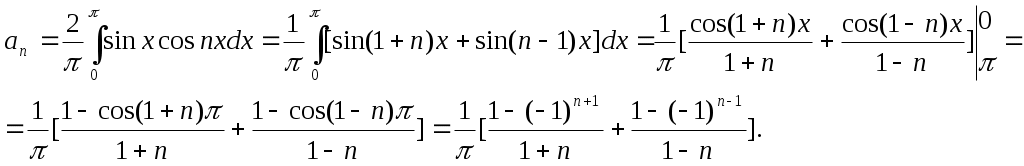
Следовательно,
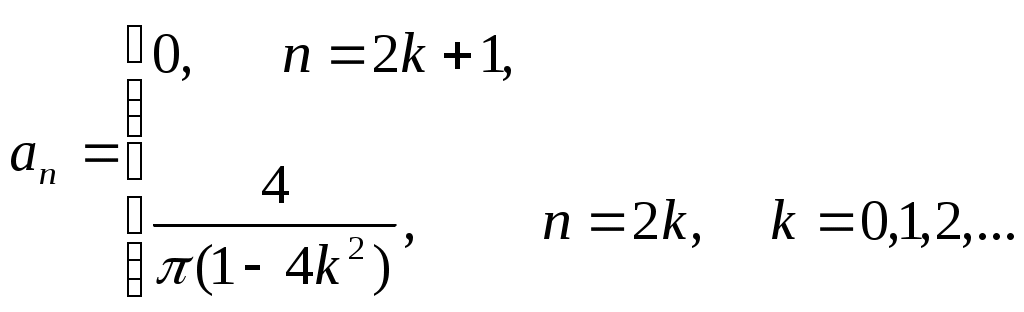
При n=1 полученное здесь общее выражение для an непригодно, вследствие чего коэффициент a1 вычисляется отдельно, полагая n=1 в общей формуле.
Представив значения коэффициентов в ряд, получим искомое разложение:

Задачи для решения
288)
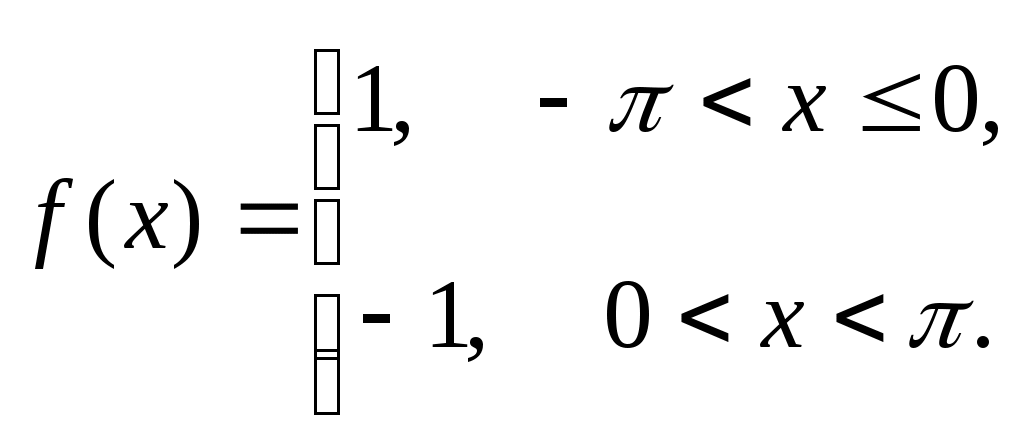
289)
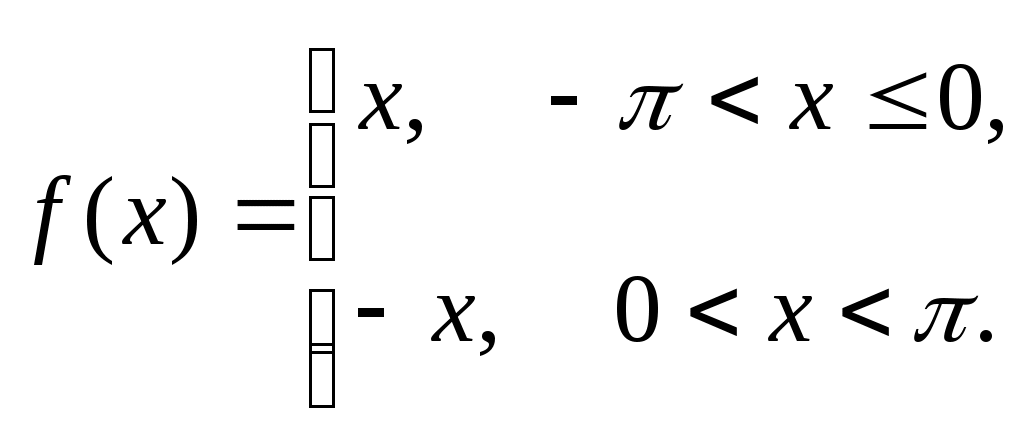
290)
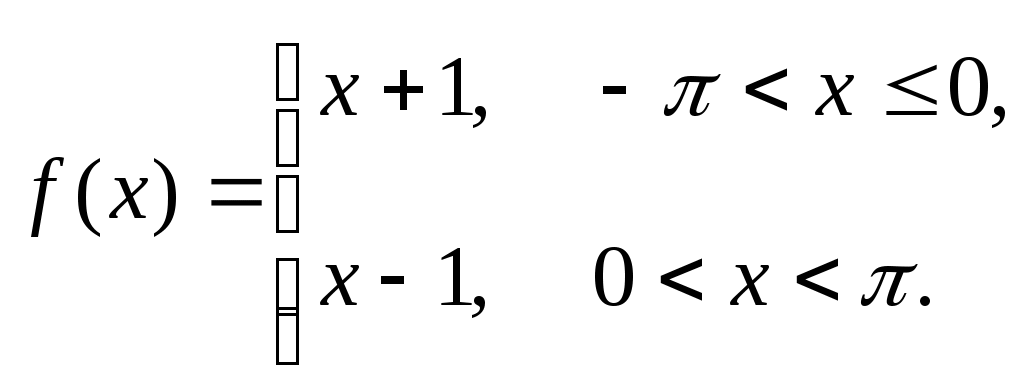
291)
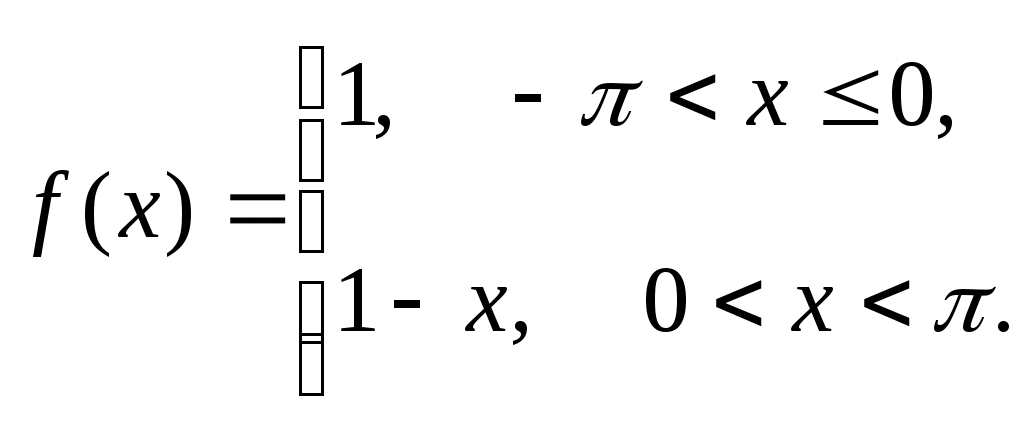
292)
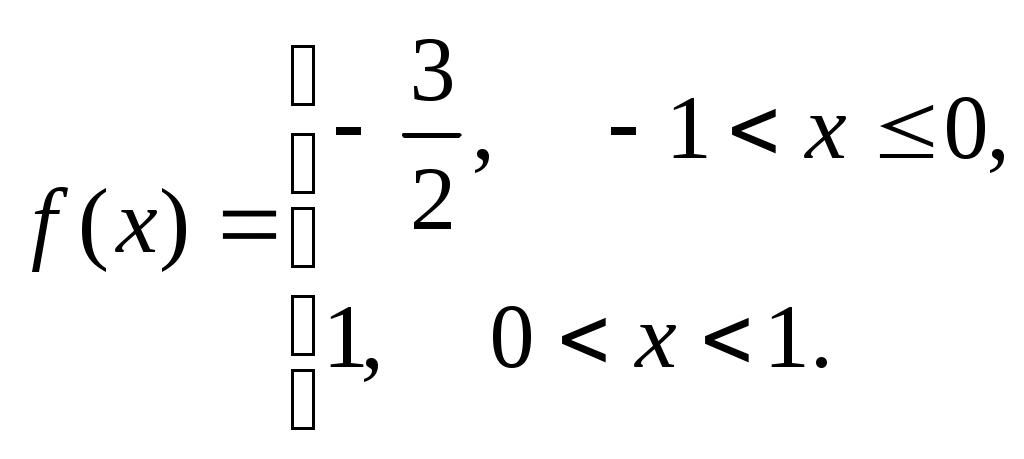
293)
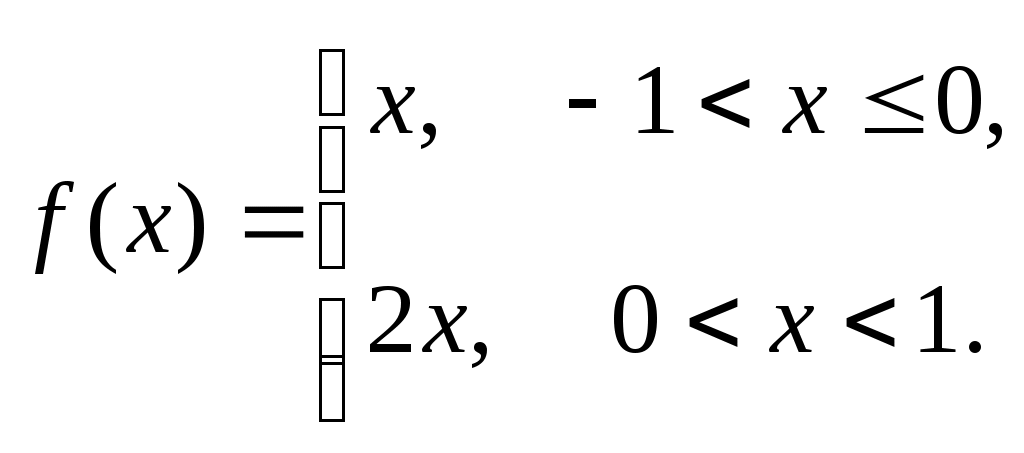
294)
295)
296)
297)
298)
299)
300)
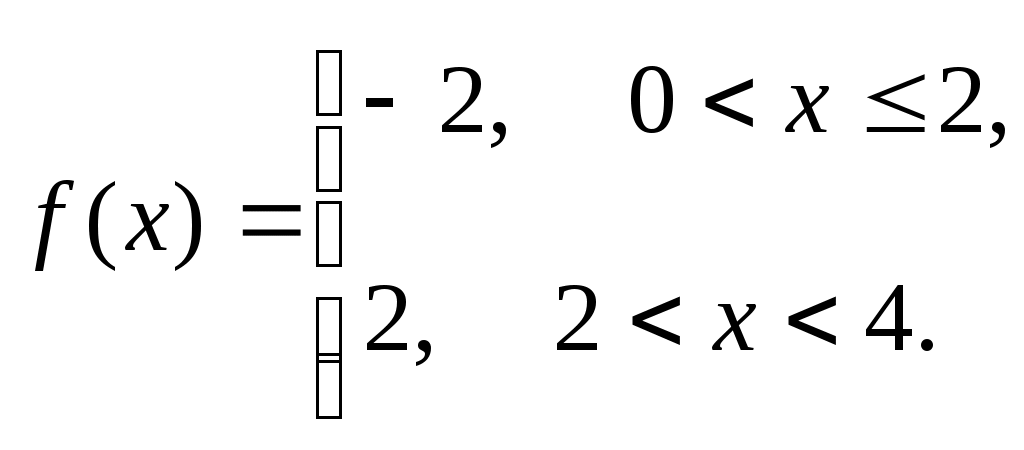
301)
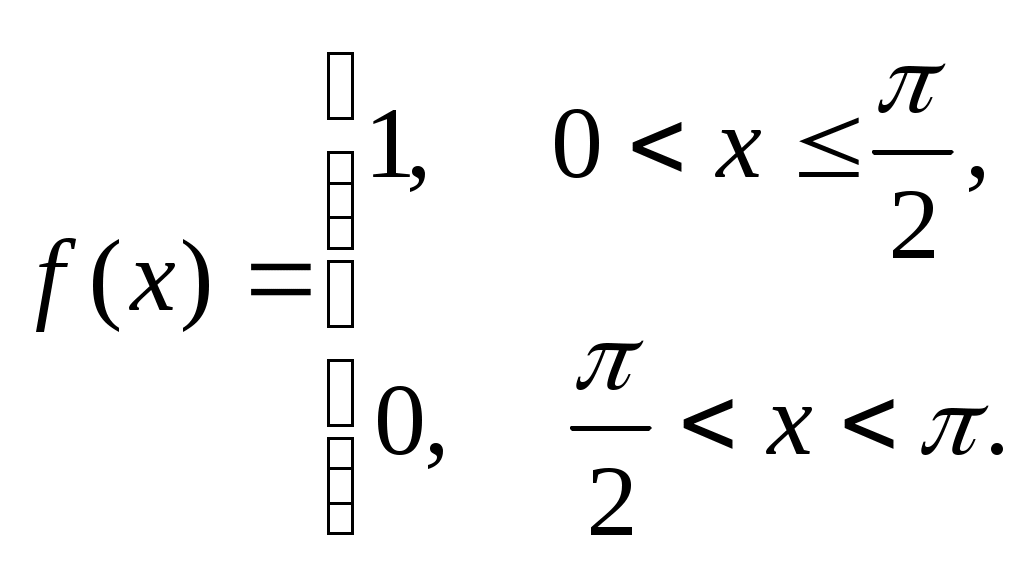 - по синусам.
- по синусам.302)
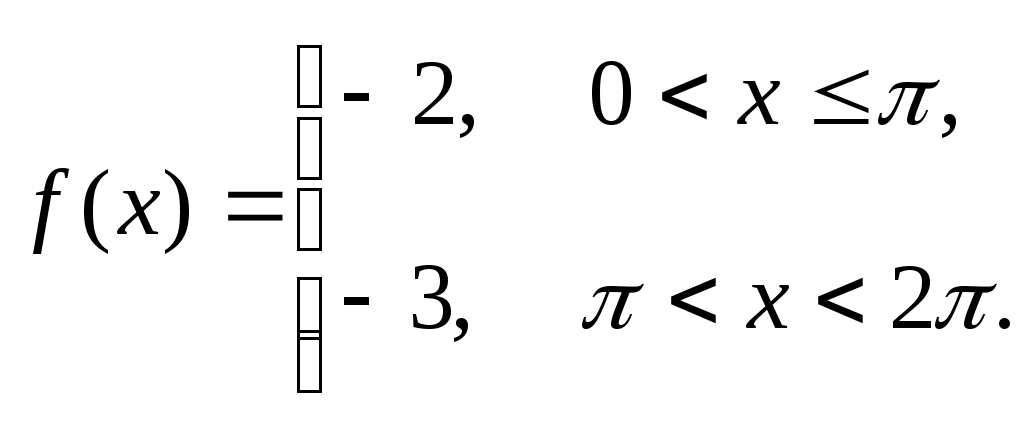
303)
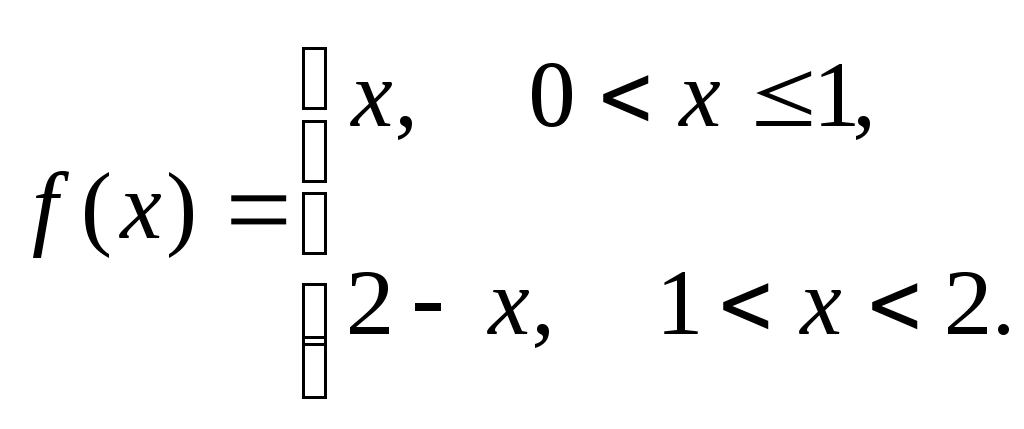 - по косинусам
- по косинусам304)
305)
306)