Файл: Сборник задач по высшей математике. РостовнаДону 2008г. 1.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 60
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
67)
68)
.69)
.70)
.71)
.72)
.В задачах 73-98 исследовать на сходимость ряды:
73)
.74)
.75)
76)
77)
78)
79)
.80)
.81)
82)
83)
84)
85)
86)
87)
88)
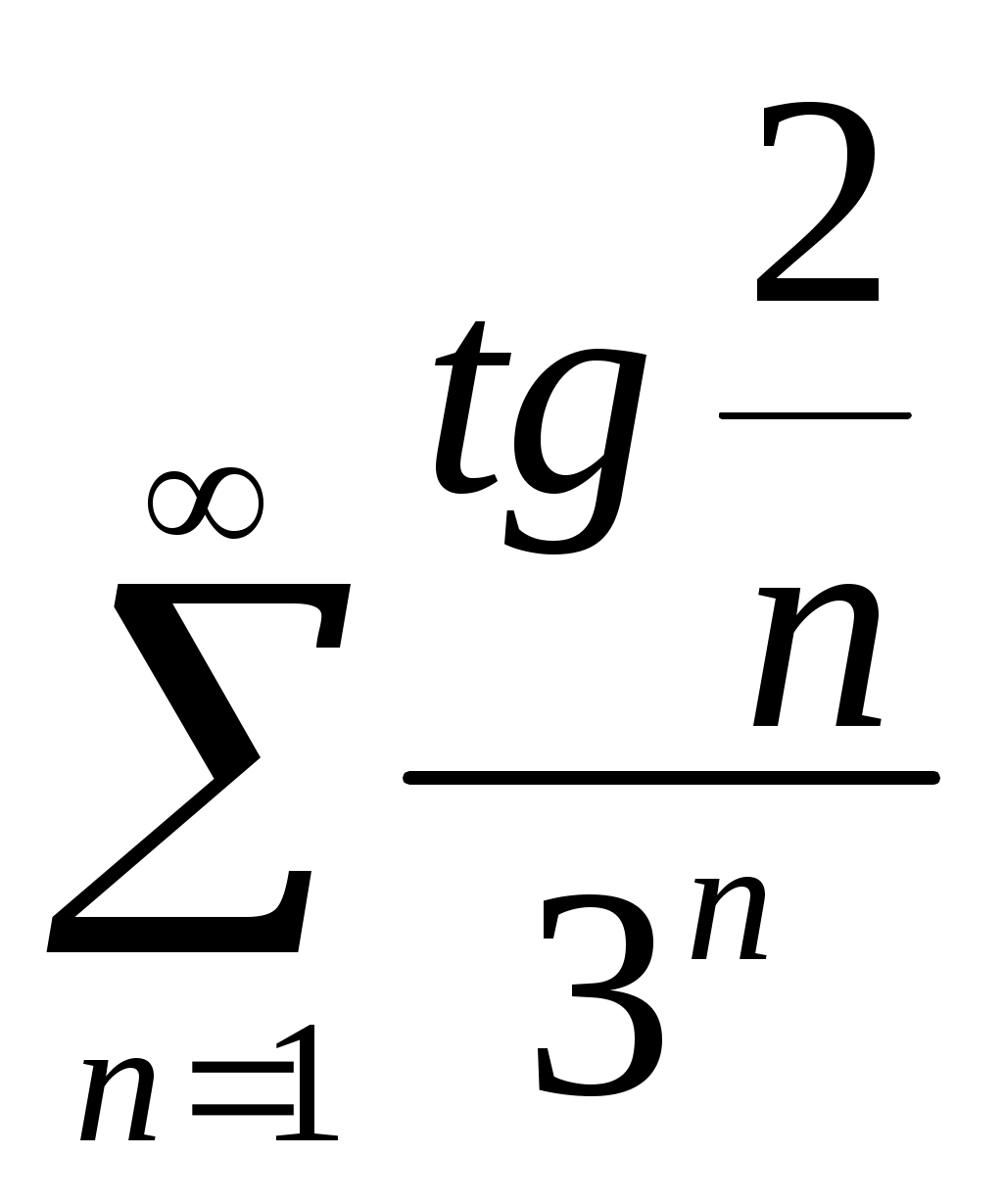
89)
90)
91)
92)
93)
94)
95)
96)
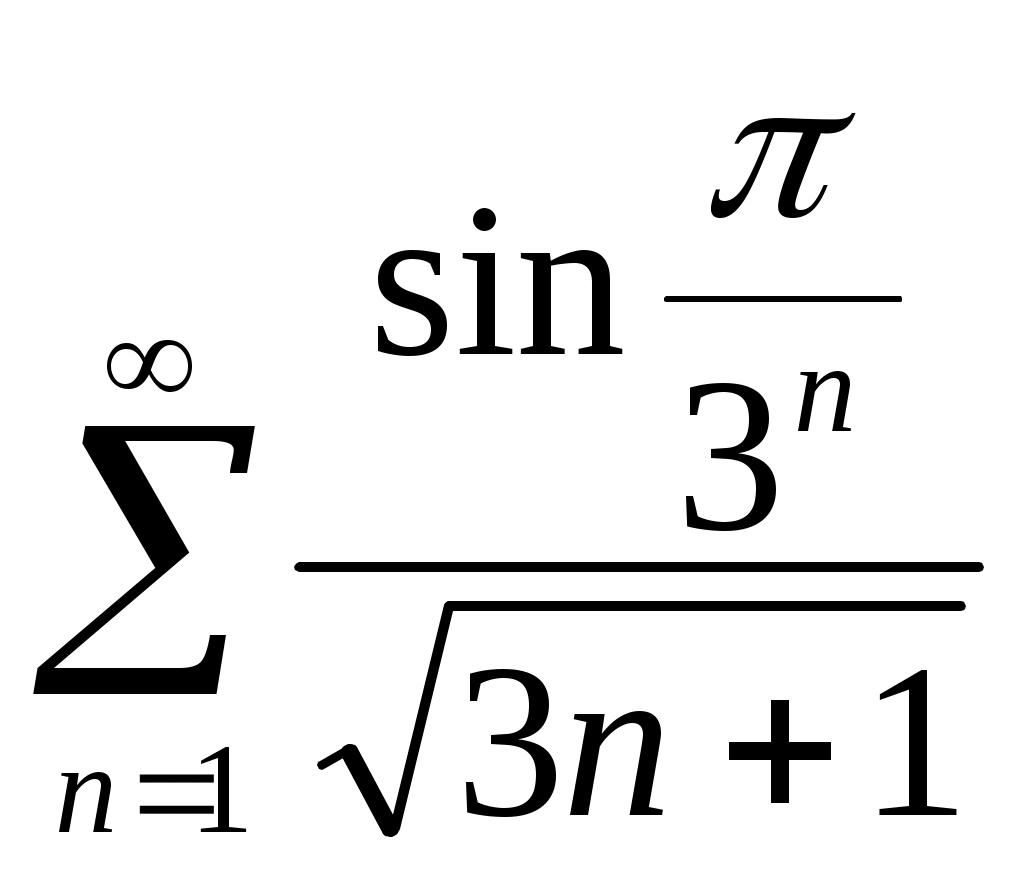
97)
98)
§2. Абсолютная и условная сходимость знакопеременных рядов. Признак сходимости знакочередующегося ряда.
Определение. Знакопеременный ряд (с членами разных знаков)
называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных значений его членов:
Знакопеременный сходящийся ряд (1) называется условно сходящимся, если ряд (2) расходится.
Всякий абсолютно сходящийся ряд, есть ряд сходящийся.
Признак Лейбница.
Знакочередующийся ряд
, 
сходится, если его члены убывают по абсолютному значению, стремясь к нулю, т.е., если
и 
При этом сумма ряда положительна и не превосходит первого члена.
Пример. Исследовать на сходимость:
1)
; 2) 
; 3) 
; 4) 
1) Члены данного знакочередующегося ряда убывают по абсолютному значению, стремясь к нулю:
и 
Поэтому, согласно признаку Лейбница, данный ряд сходится. Чтобы установить, сходится ли абсолютно или условно, исследуем ряд с положительными членами
, составленный из абсолютных значений членов данного ряда. Применим предельный признак сравнения. Рядом сравнения к ряду является расходящийся гармонический ряд 
(т.к. 
)Следовательно, ряд из абсолютных значений членов ряда расходится, а значит, исходный ряд сходится условно.
2) Заменим члены данного знакопеременного ряда, где
- любое число, их абсолютными значениями и исследуем полученный ряд 
с положительными членами. Сравним его с геометрической бесконечно убывающей прогрессией
, которая является сходящимся рядом. Каждый член полученного ряда не превосходит соответствующего члена геометрической прогрессии.
Поэтому согласно признаку сравнения ряд с положительными членами также сходится, а заданный знакопеременный ряд сходится абсолютно.
3) Члены данного знакочередующегося ряда убывают по абсолютному значению, стремясь к нулю:
, 
Поэтому согласно признаку Лейбница, он сходится. Ряд
также сходится согласно признаку Даламбера: 
Следовательно, данный ряд абсолютно сходится.
4) Для данного знакопеременного ряда не выполняется необходимое условие сходимости:
- не существует.Следовательно, ряд расходится.
Задачи для решения.
В задачах 99-128 выяснить, сходится ли абсолютно
, условно или расходится ряд:
99)
100)
101)
102)
103)
104)
105)
106)
107)
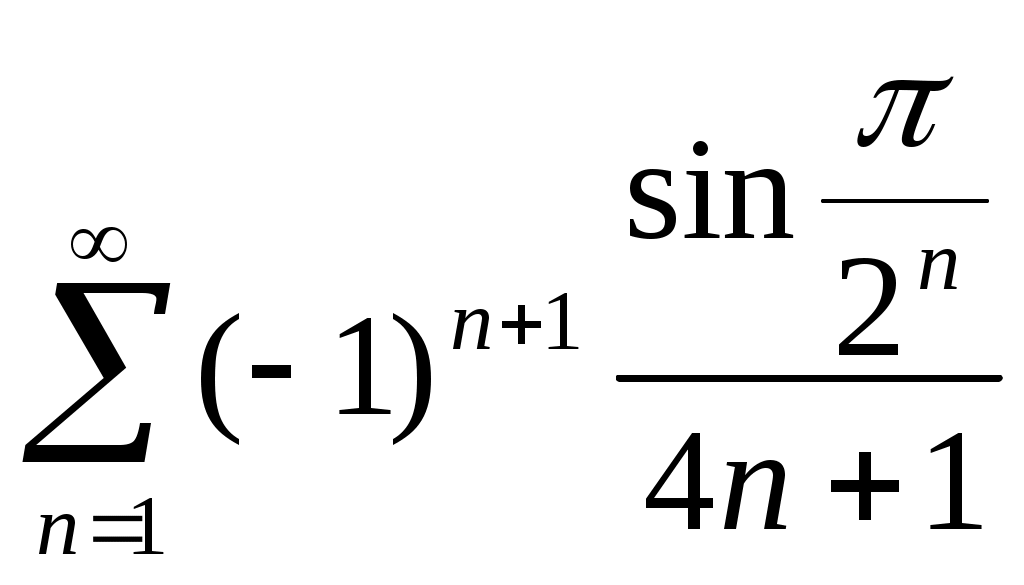
108)
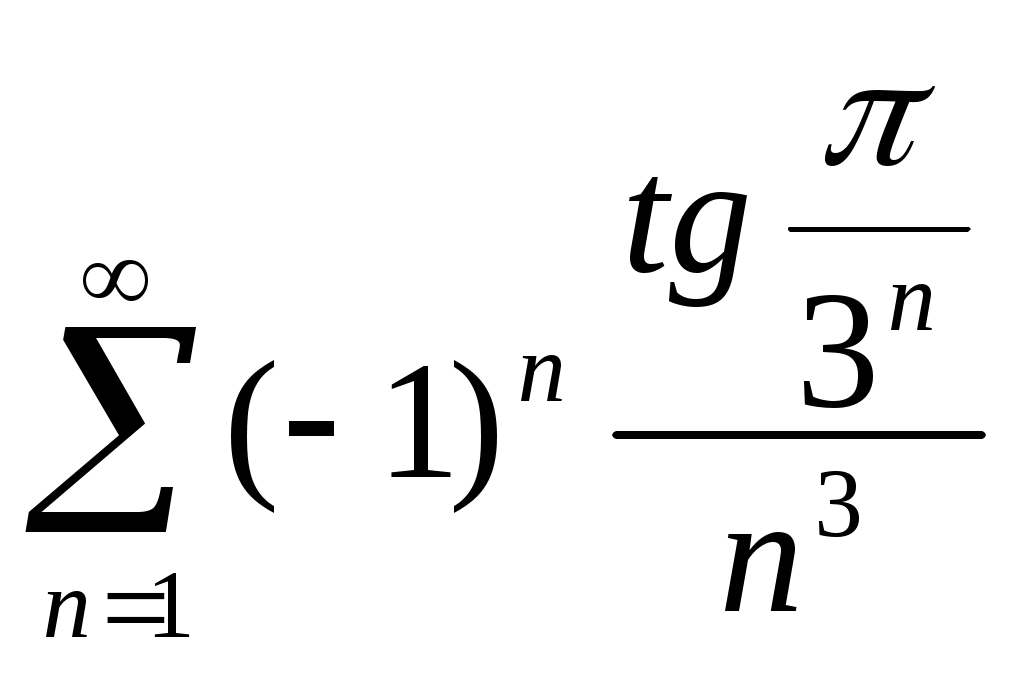
109)
110)
111)
112)
113)
114)
115)
116)
117)
118)
119)
120)
121)
122)
123)
124)
125)
126)
127)
128)
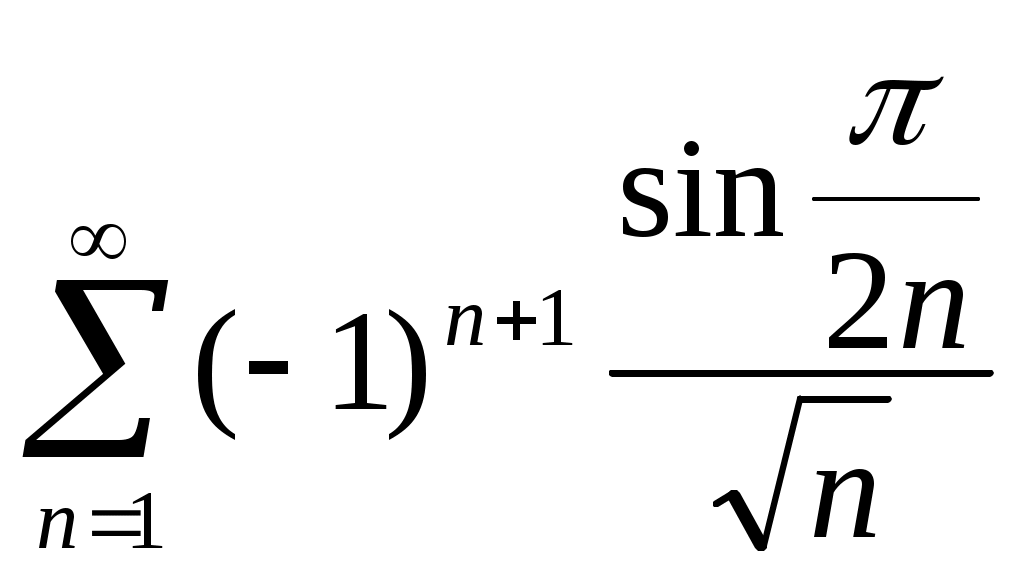
1>1>