Файл: Сборник задач по высшей математике. РостовнаДону 2008г. 1.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 59
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
; 2) 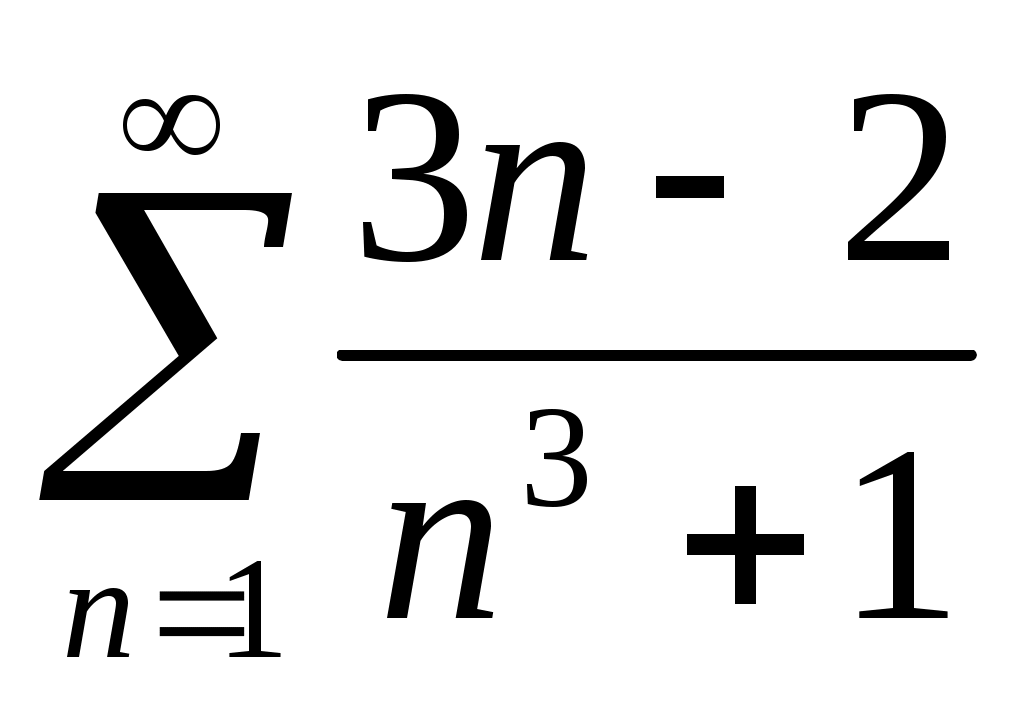
1) Рядом сравнения будет гармонический ряд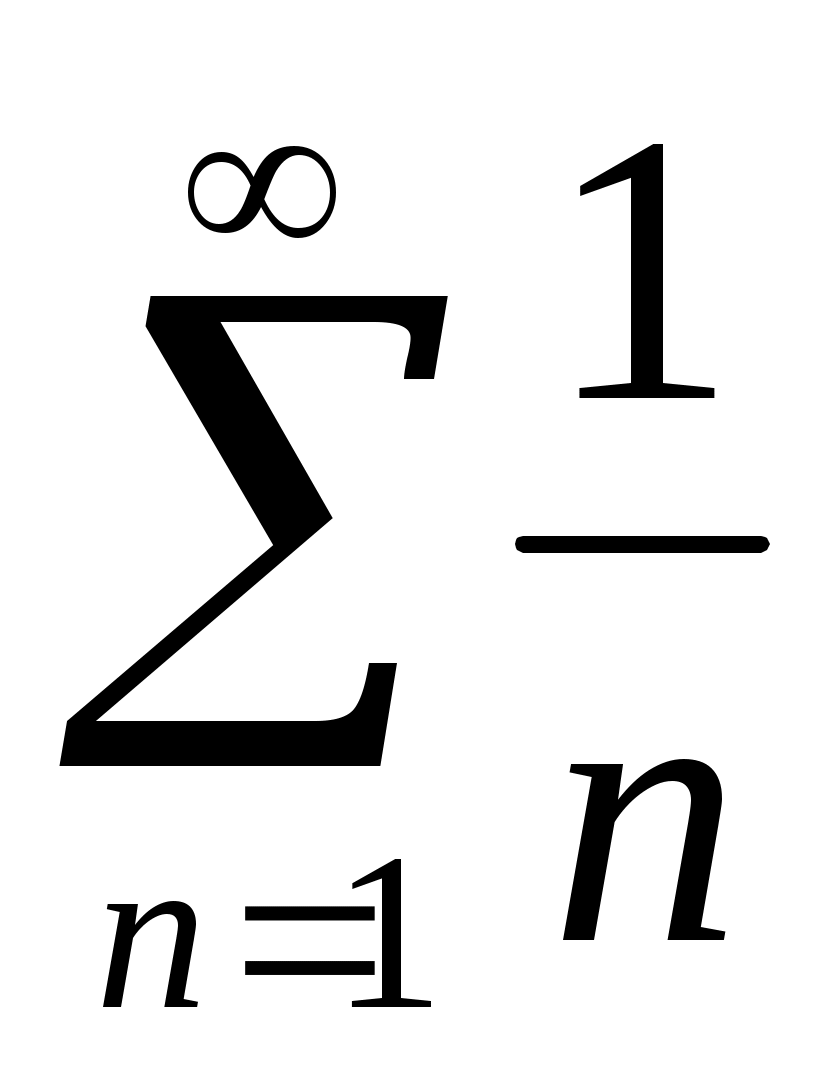 . Действительно,
. Действительно,
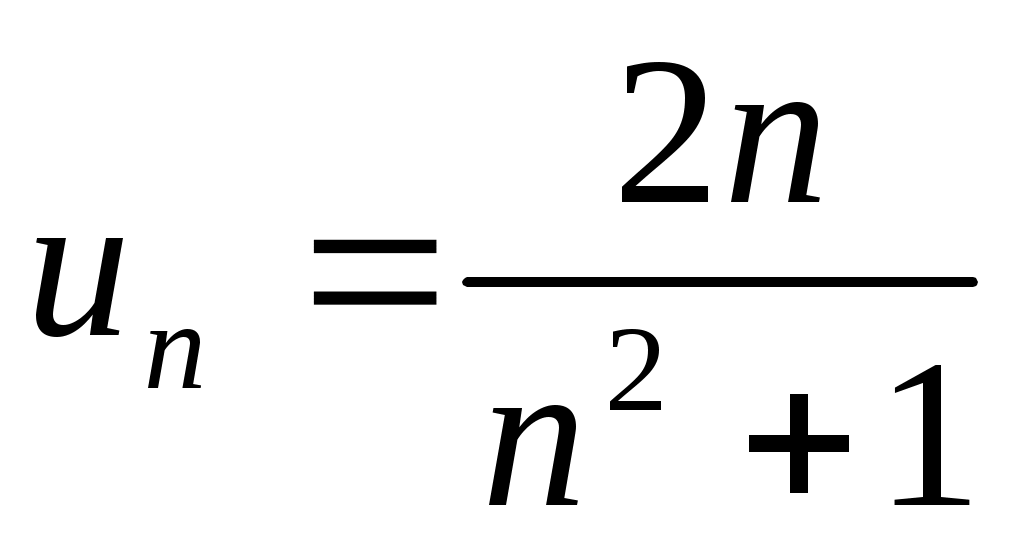 ,
, 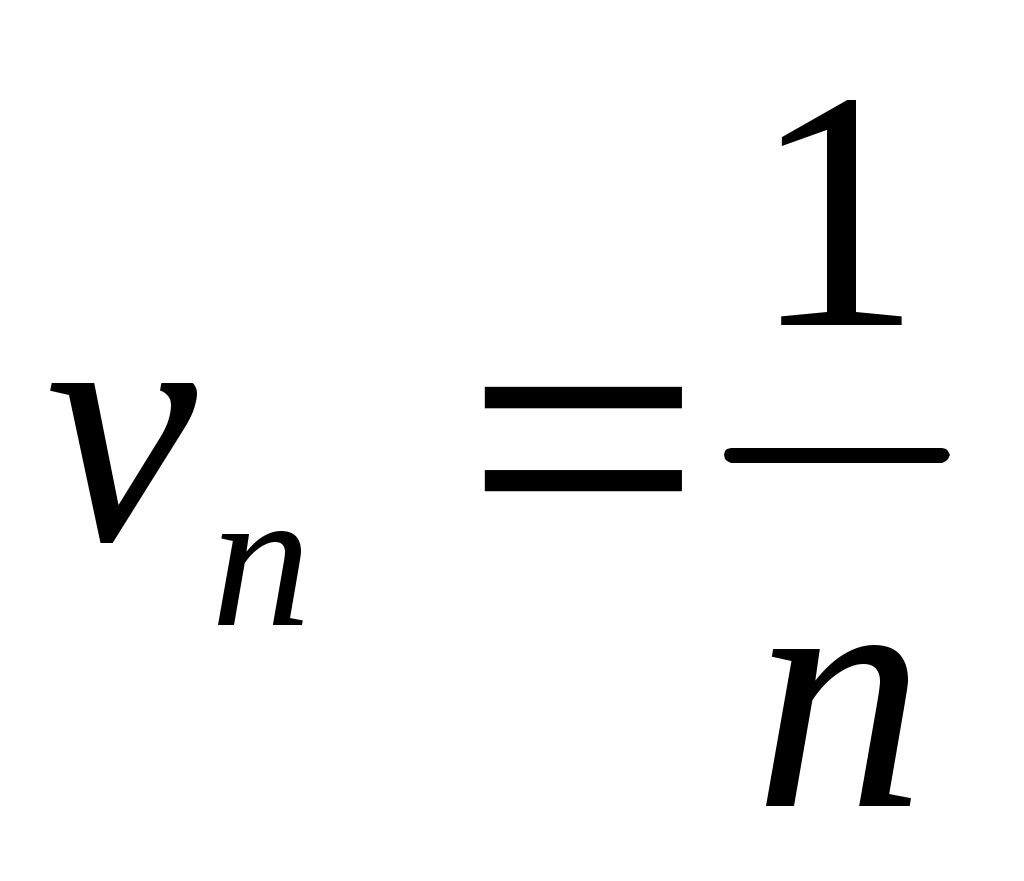 ,
, 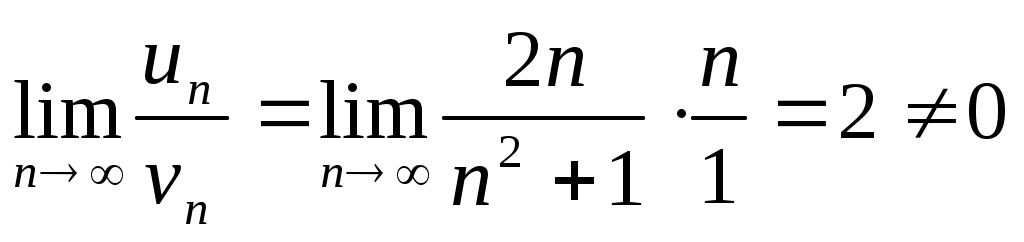 ,
,
следовательно, ряды ведут себя одинаково, а т.к. гармонический ряд расходится, то и данный ряд также расходится.
2) В качестве ряда сравнения выберем обобщенный гармонический ряд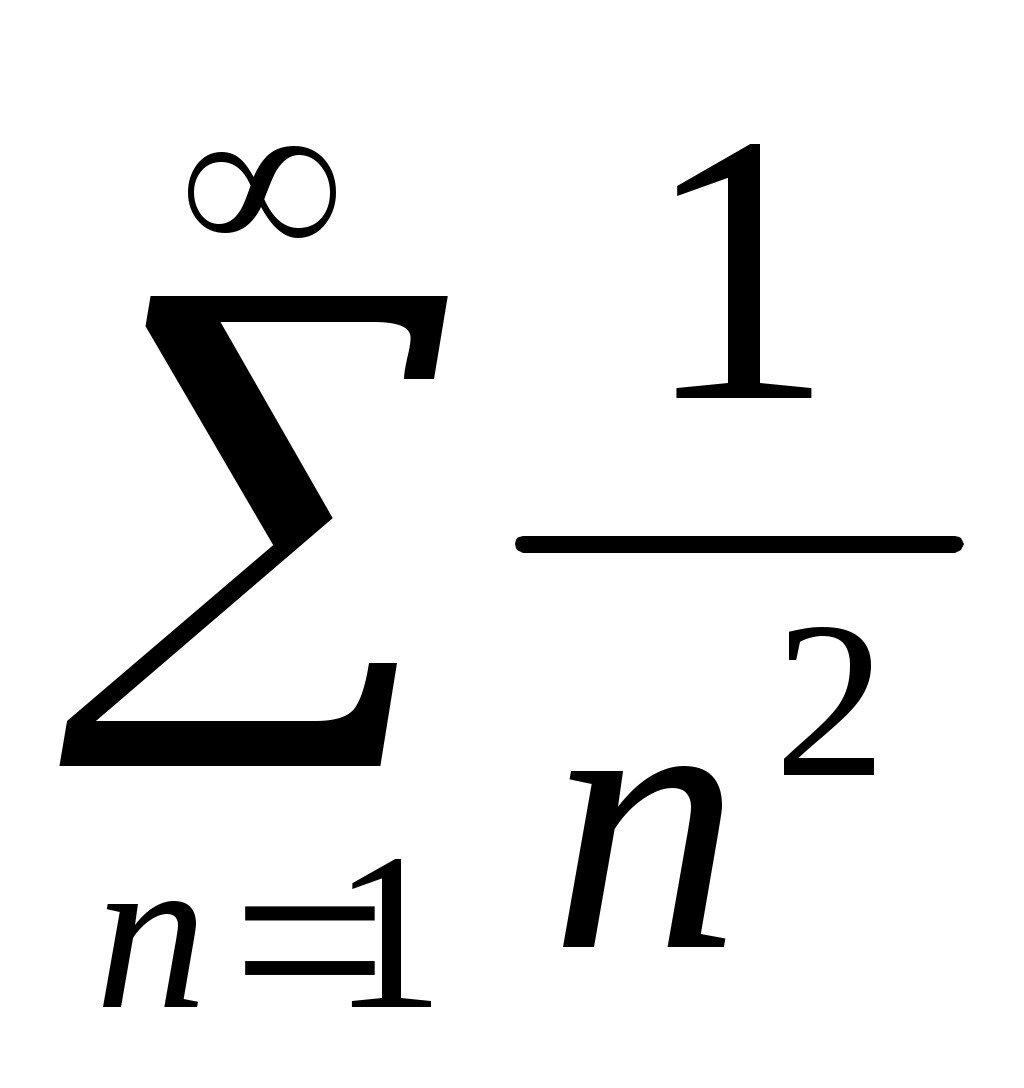 , поскольку
, поскольку
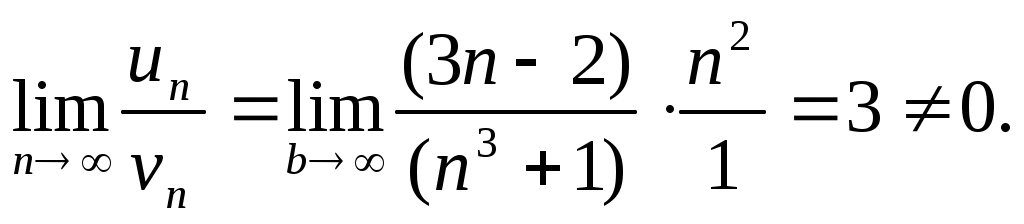 Ряд
Ряд 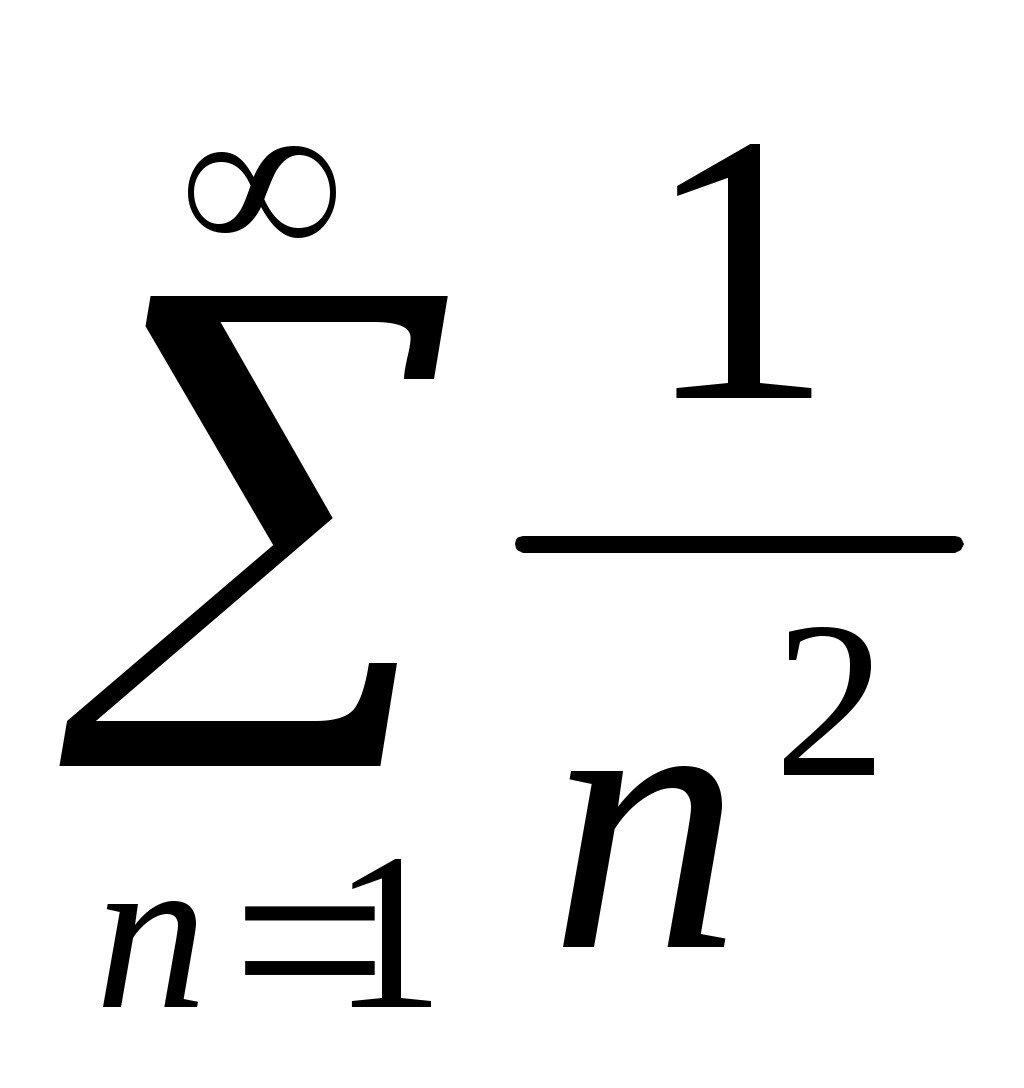 сходится.
сходится.
(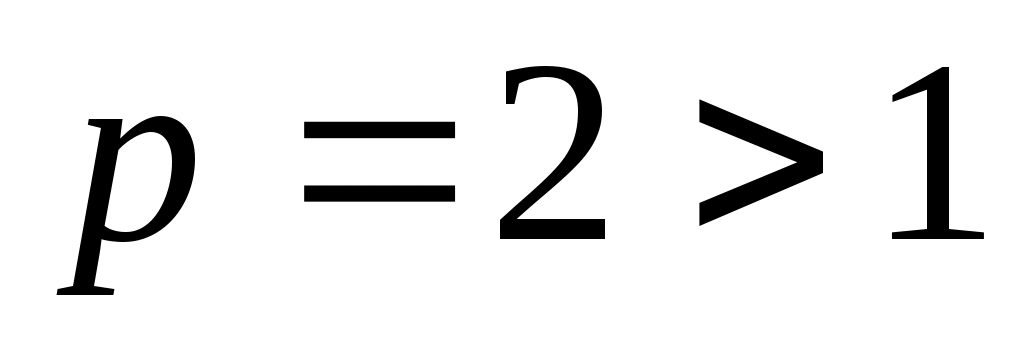 ), поэтому сходится и рассматриваемый ряд.
), поэтому сходится и рассматриваемый ряд.
Из примеров следует вывод:
Чтобы выбрать ряд сравнения, нужно разделить старшую степень числителя на старшую степень знаменателя; образовавшийся после сокращения обобщенный гармонический ряд и есть ряд сравнения.
2. Признак Даламбера.
Если для знакоположительного ряда существует конечный предел
существует конечный предел
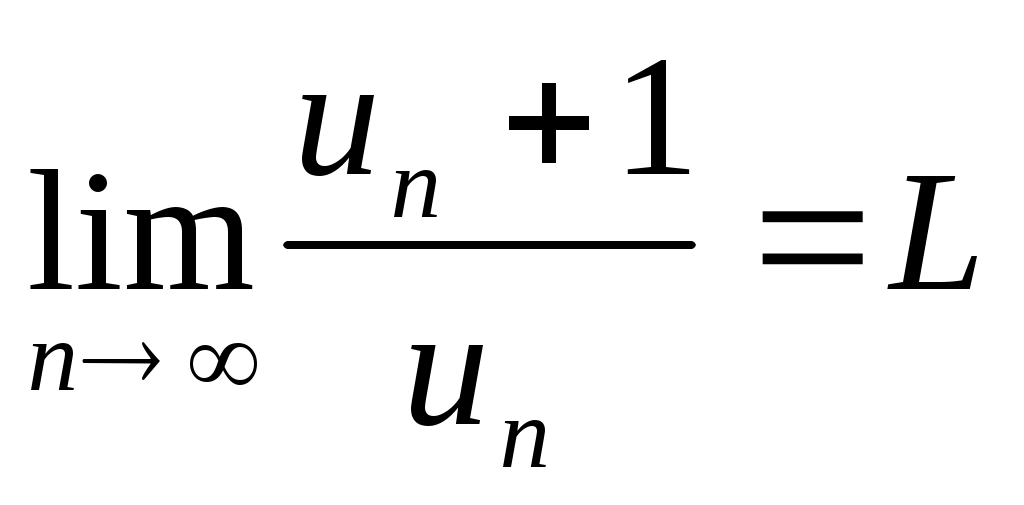
то при 1) L<1 ряд сходится; 2) L>1 ряд расходится; 3) L=1 признак ответа не дает.
Признак Даламбера обычно применяется в том случае, когда общий член ряда содержит факториалы, показательную функцию от n, синус или тангенс бесконечно малого аргумента.
Пример. Исследовать на сходимость:
1)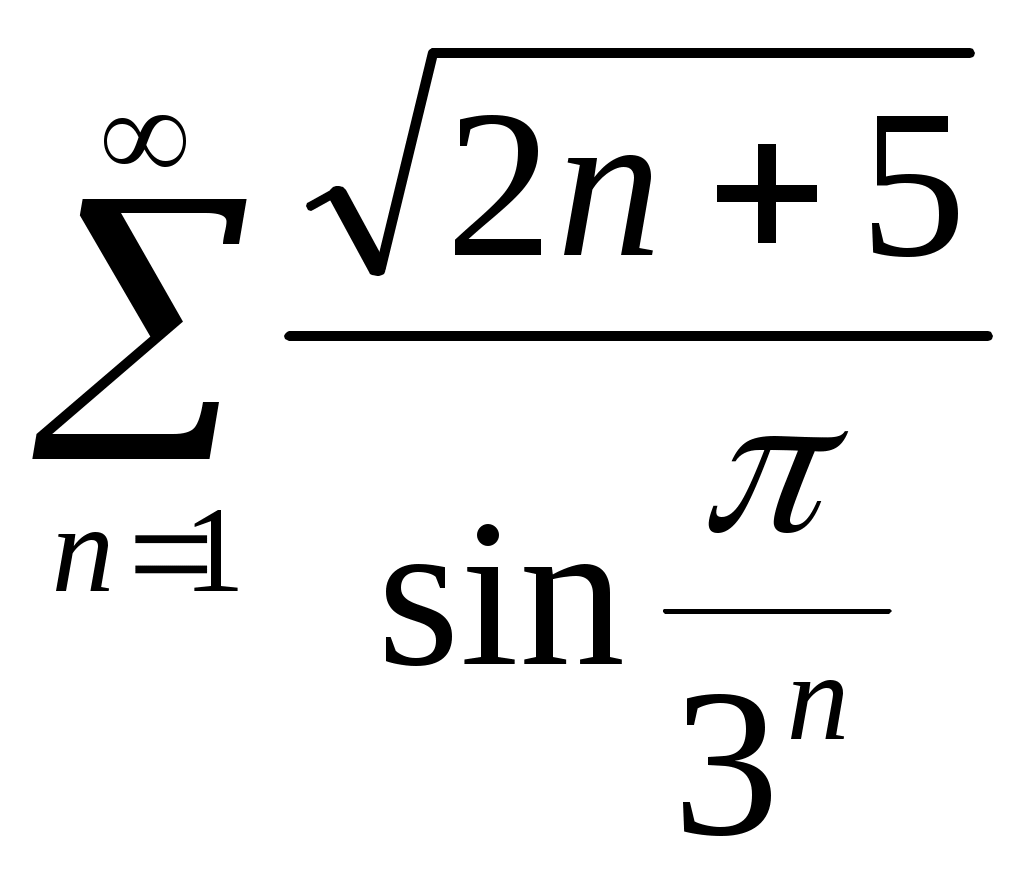 , 2)
, 2) 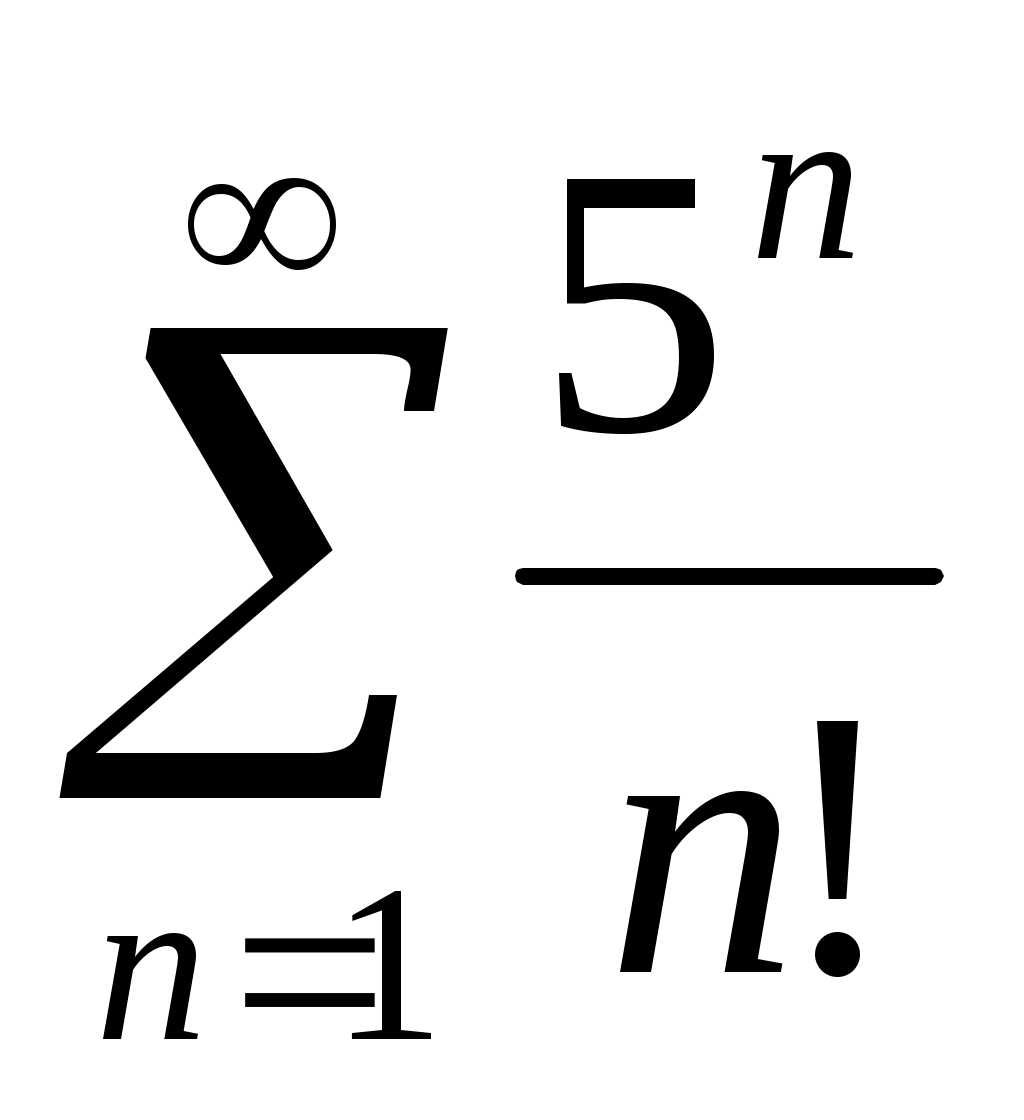
1) Т.к.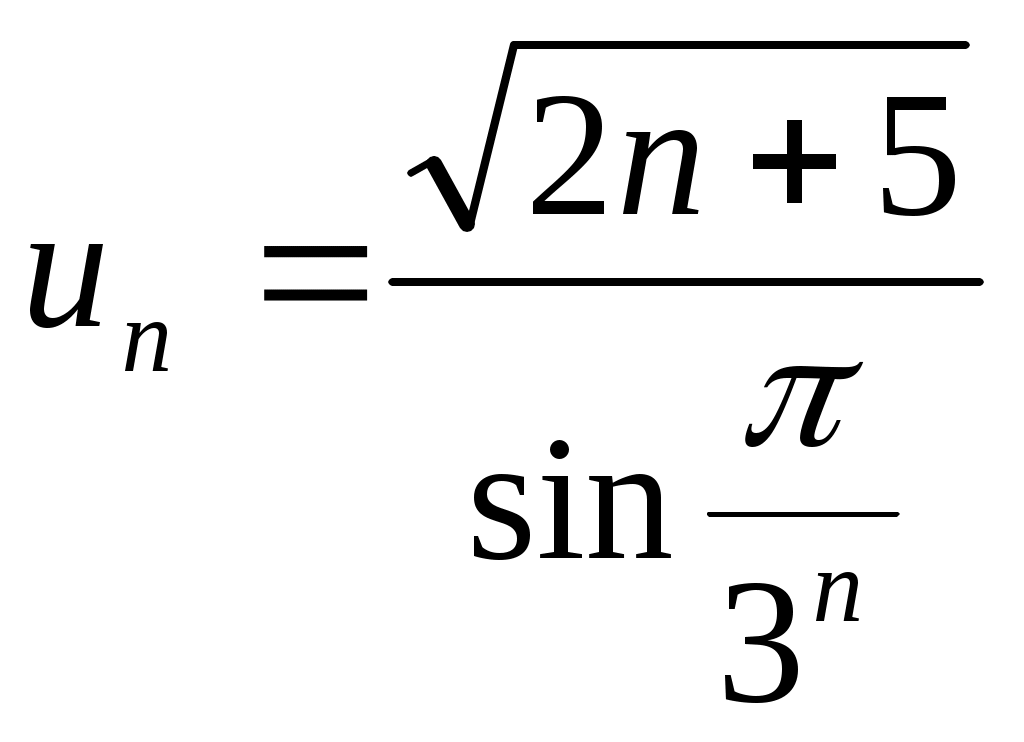 , то
, то 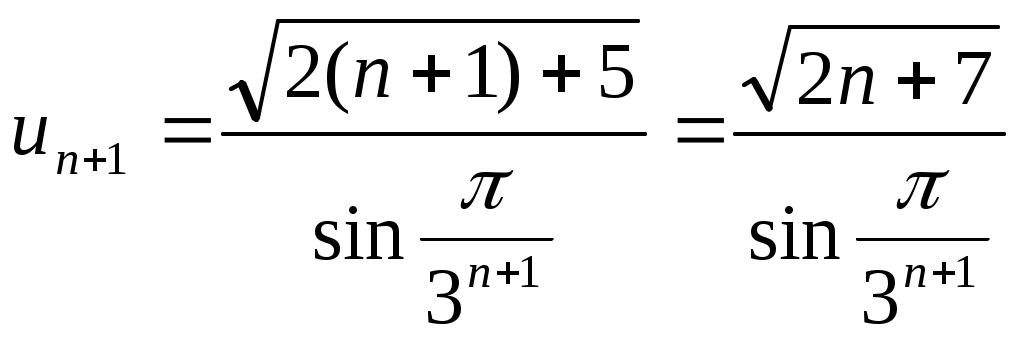
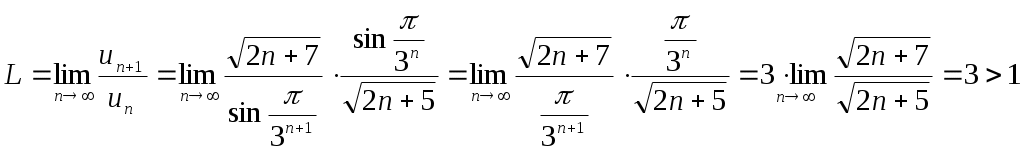 - ряд расходится.
- ряд расходится.
2)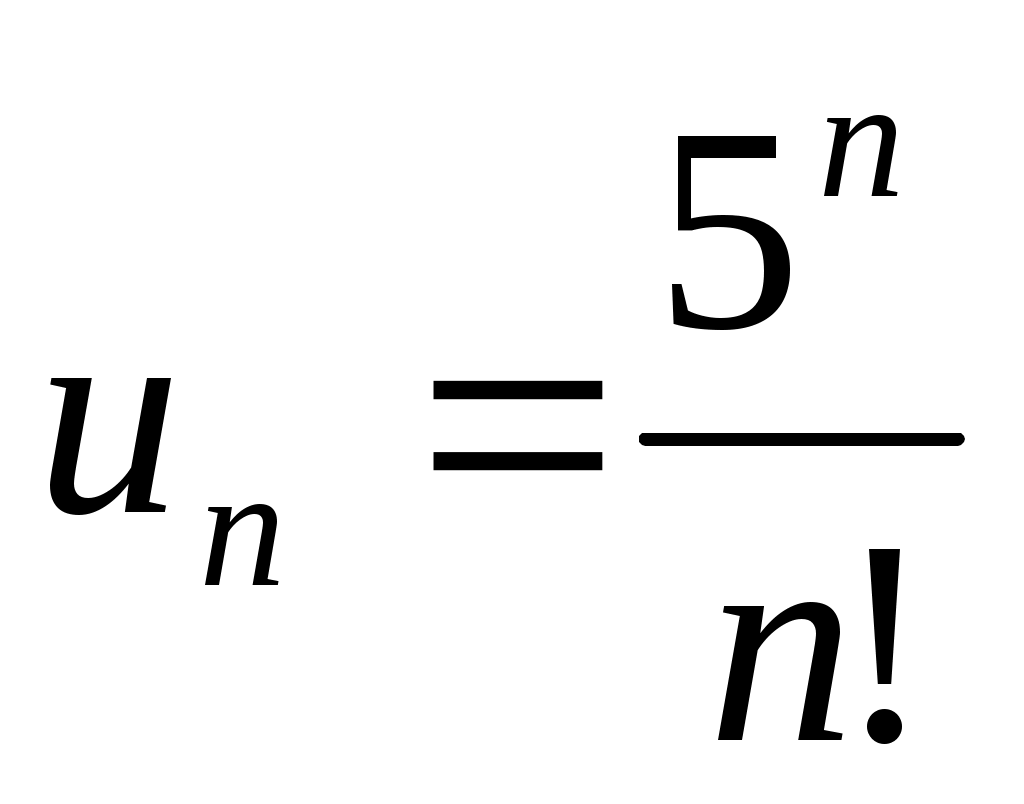
;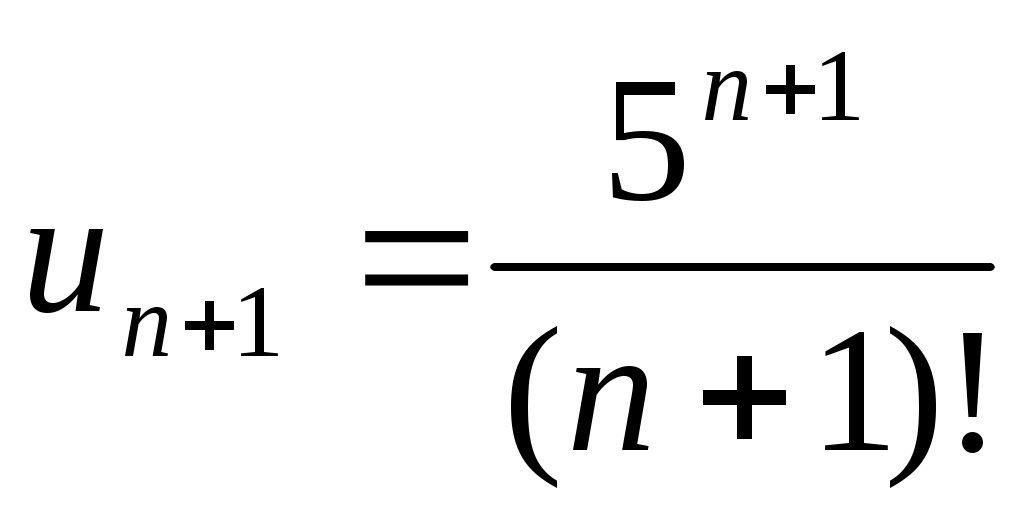
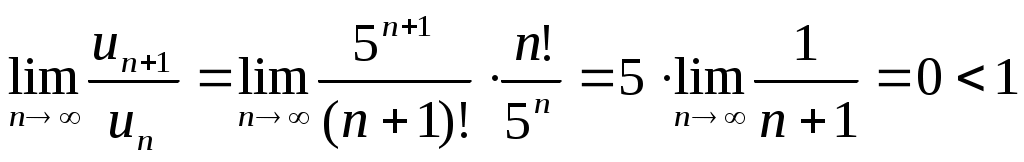 - ряд расходится.
- ряд расходится.
3. Интегральный признак Коши.
Пусть члены ряда u1, u2, u3,..., un,... положительны и не возрастают, т.е.
u1 ≥u2≥ u3≥...
и пусть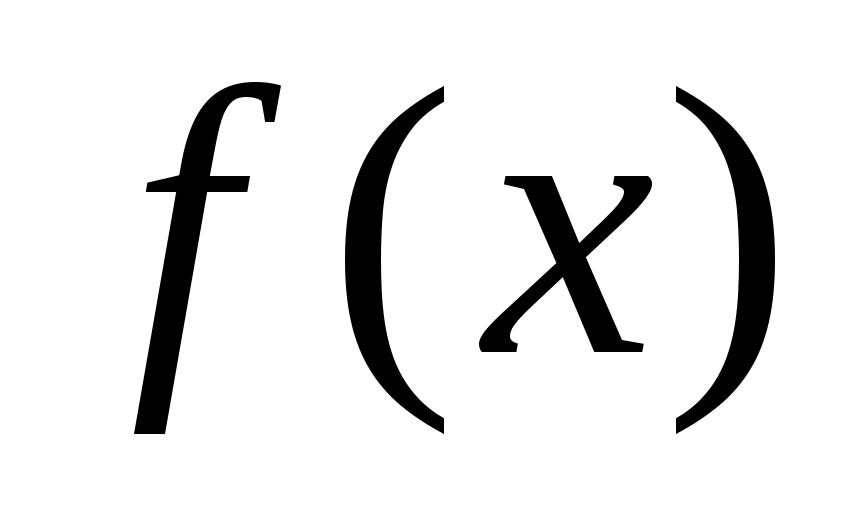 - такая непрерывная невозрастающая функция, что
- такая непрерывная невозрастающая функция, что
f(1)=u1; f(2)=u2;...; f(n)=un
Тогда:
Пример. Исследовать на сходимость:
 ;
; 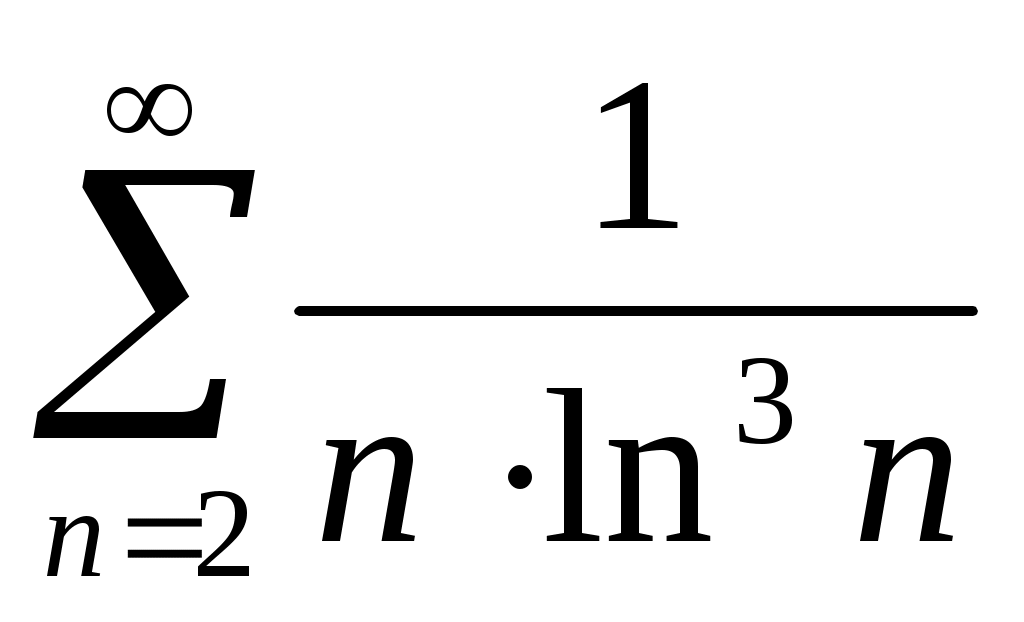 .
.
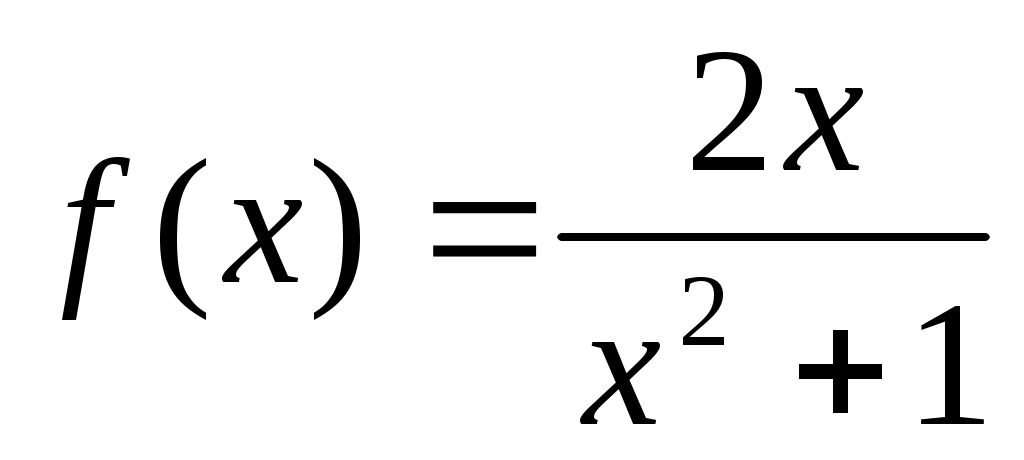
является непрерывной и убывающей на всем бесконечном интервале изменения x. Затем находим несобственный интеграл от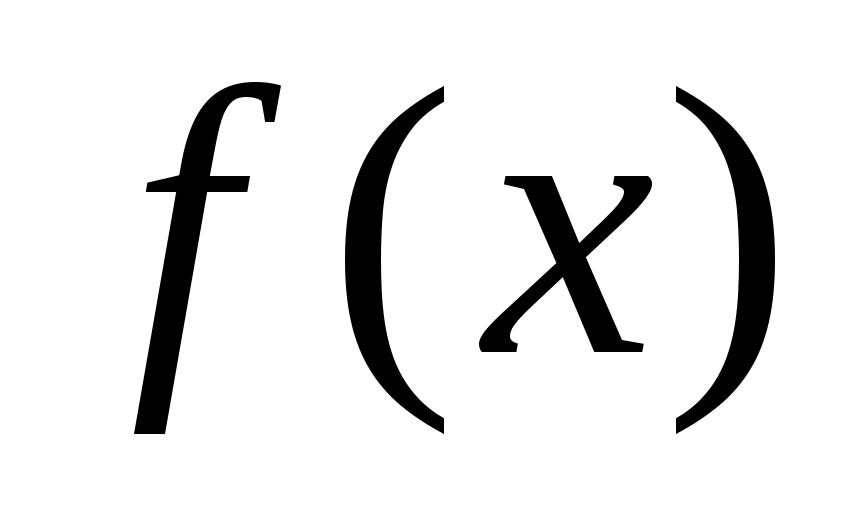 с бесконечным верхним пределом:
с бесконечным верхним пределом:
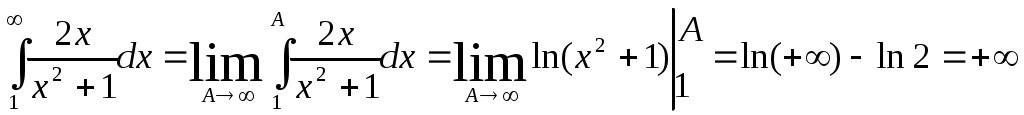
Несобственный интеграл расходится, следовательно, и данный ряд также расходится.
2)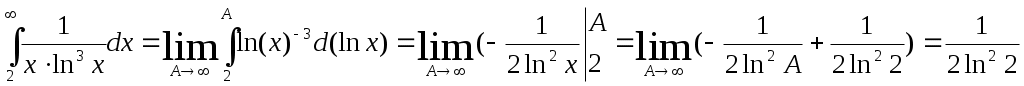
Несобственный интеграл сходится, следовательно, и рассматриваемый ряд также сходится.
4. Радикальный признак Коши.
Если для знакоположительного ряда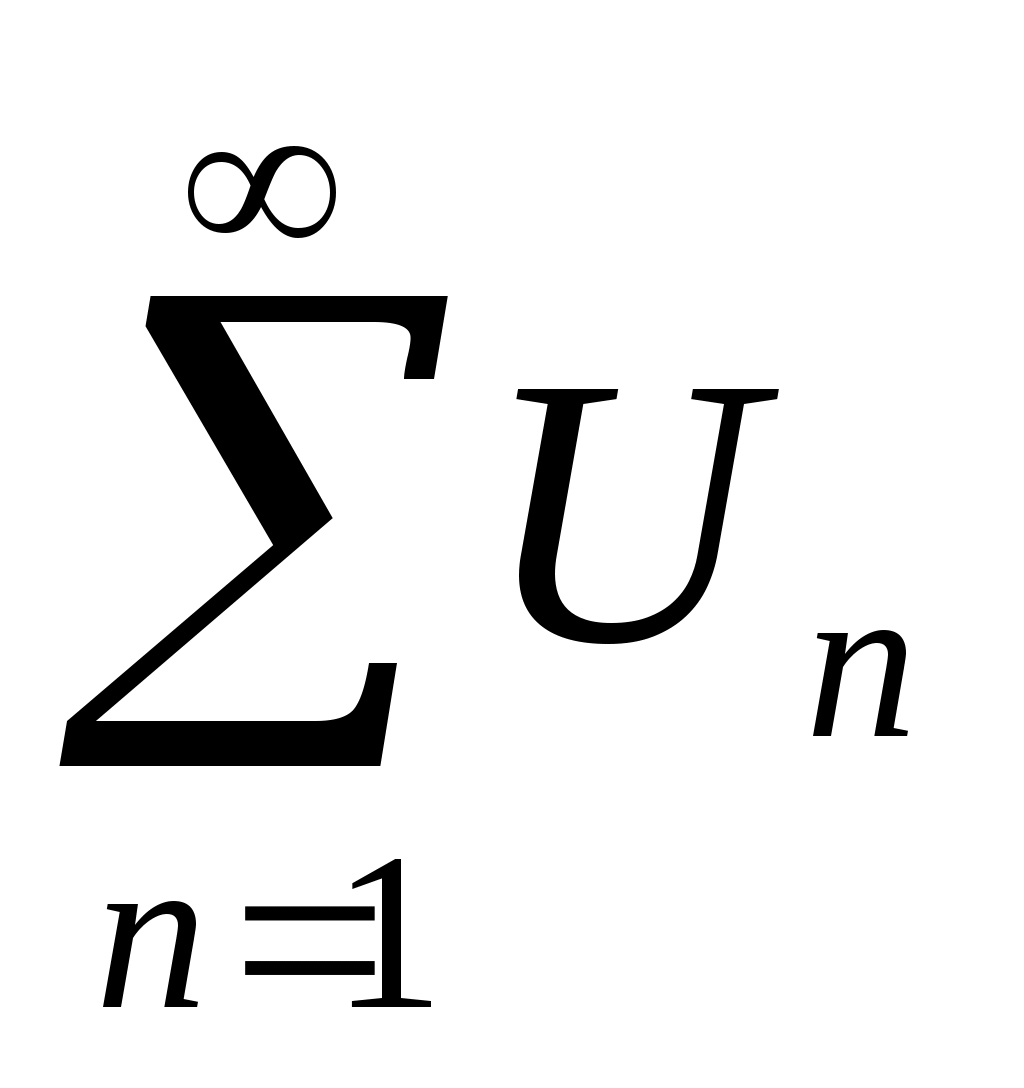 существует предел
существует предел 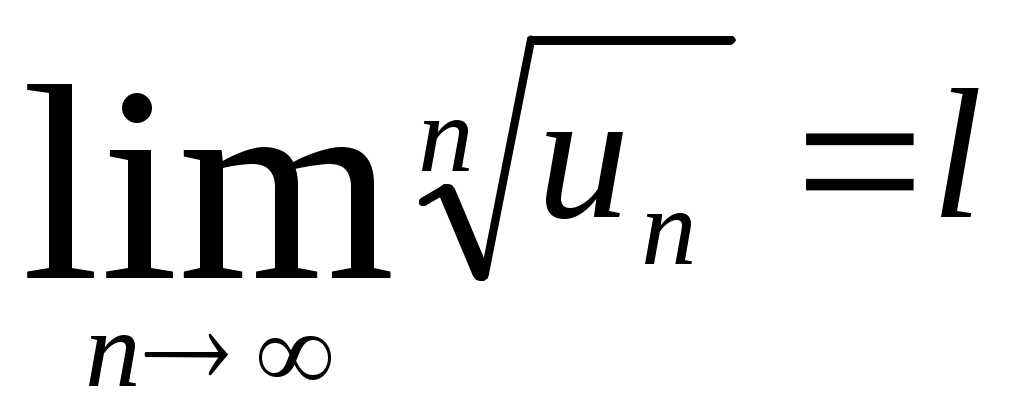 ,
,
то при l<1 ряд сходится, а при l>1 расходится; при l=1 признак ответа не дает.
Пример. Исследовать на сходимость:
1)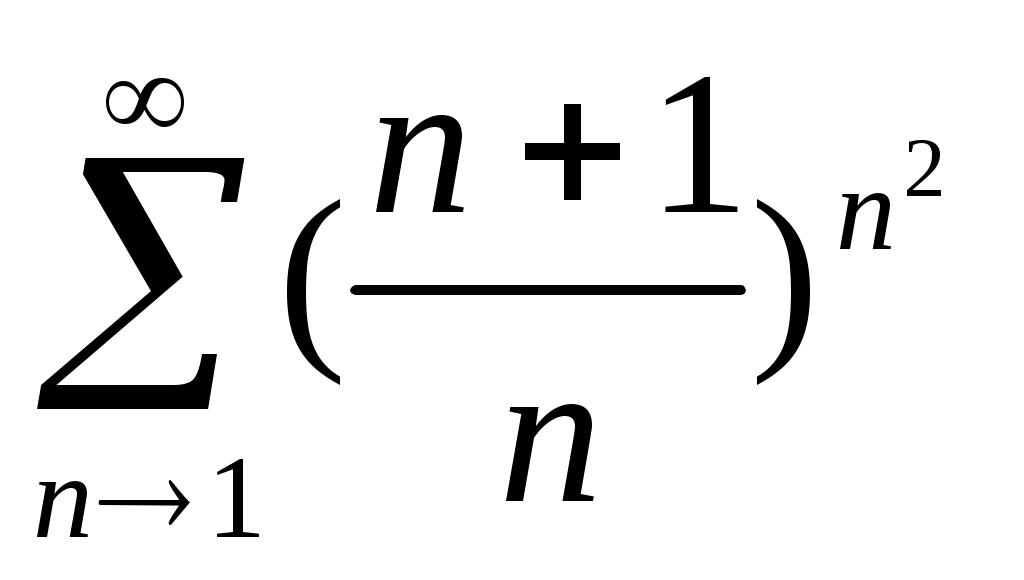
; 2)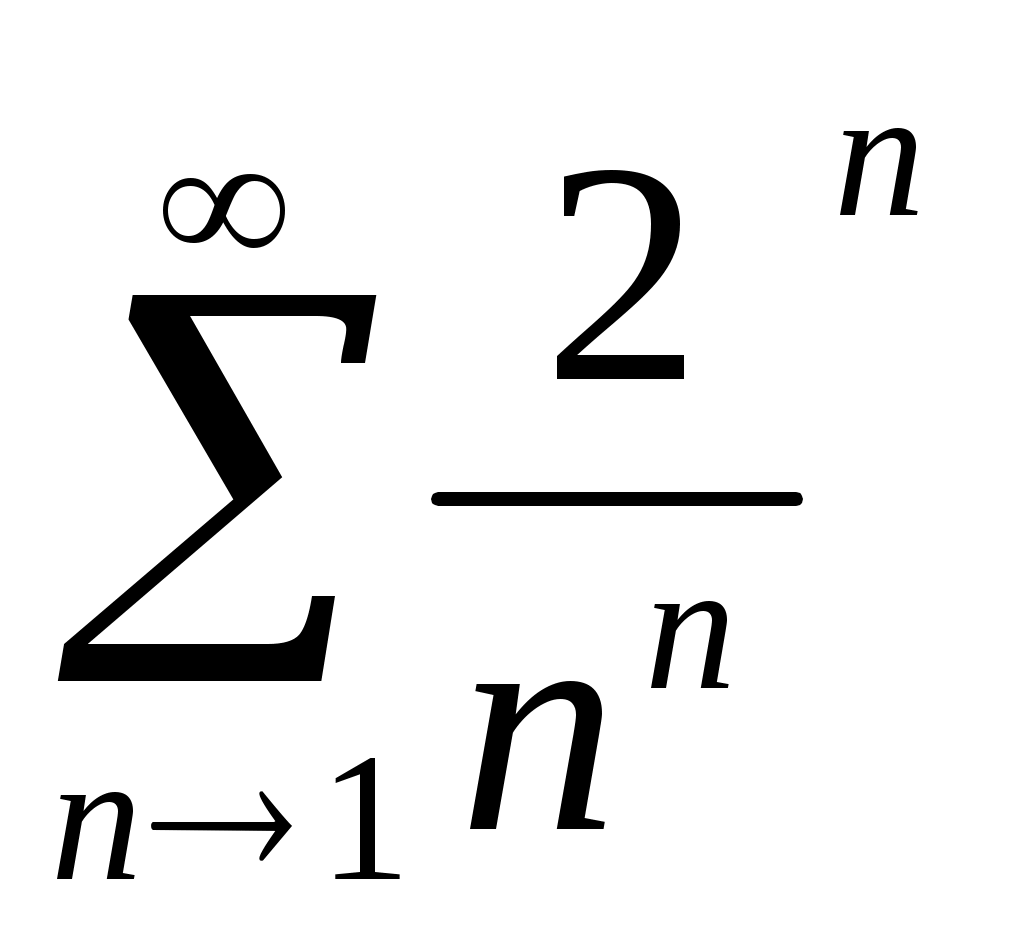
Решение:
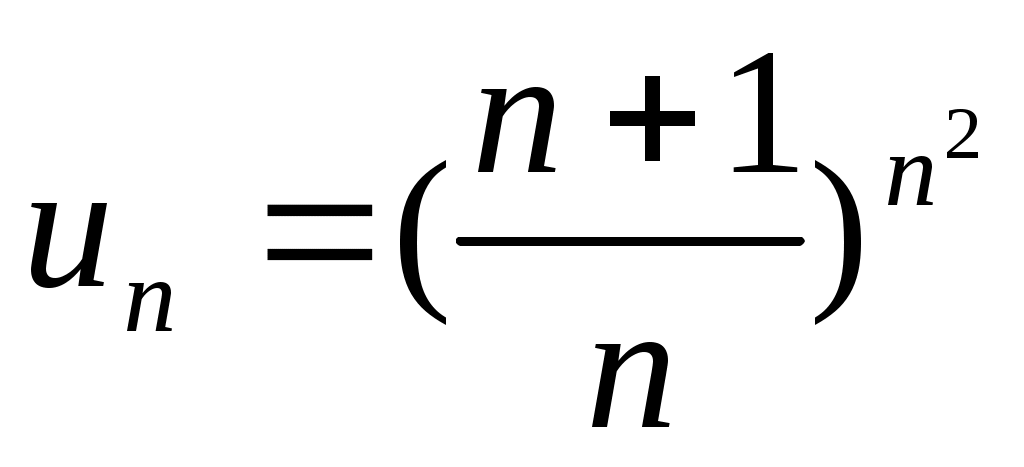 ;
;
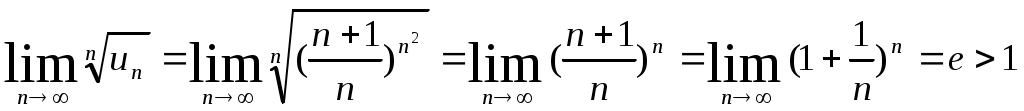 .
.
Следовательно, исходный ряд расходится.
2)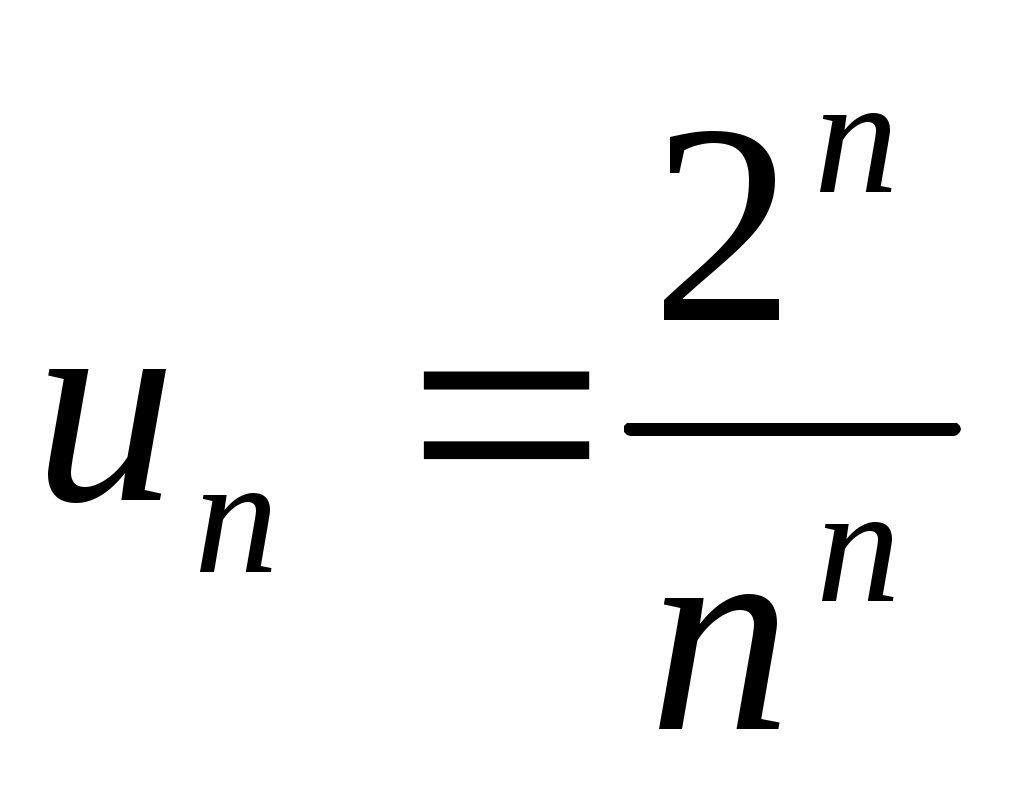 ;
;
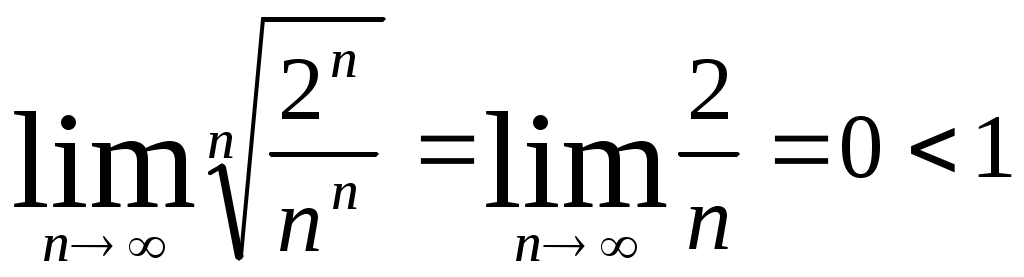 ,
,
следовательно, рассмотренный ряд является сходящимся.
Задачи для решения.
В задачах 1-10 написать формулу n-ого члена ряда.
1)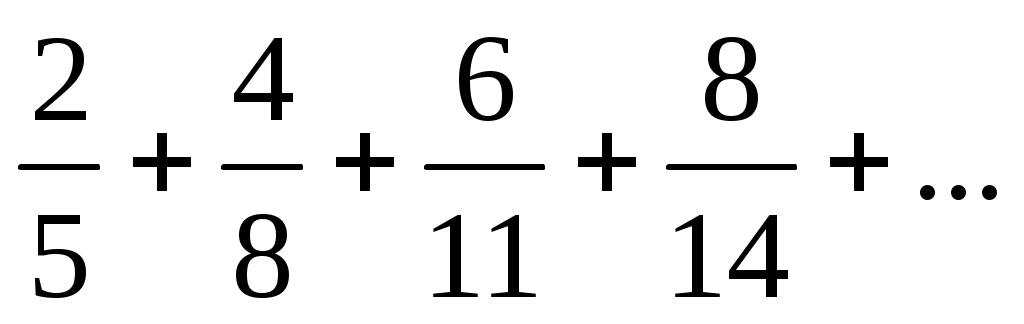
2)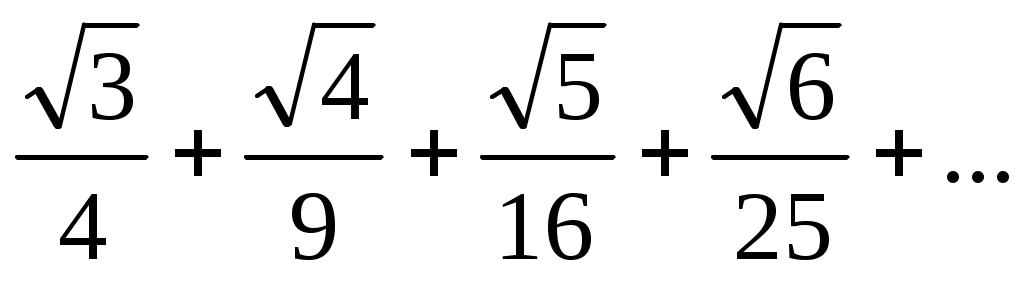
3)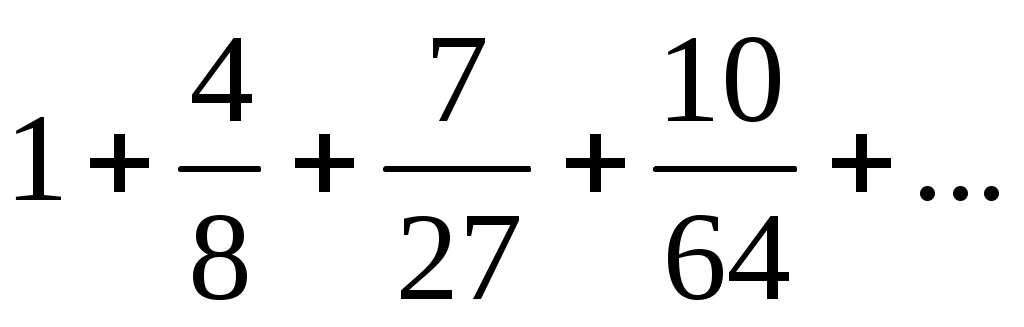
4)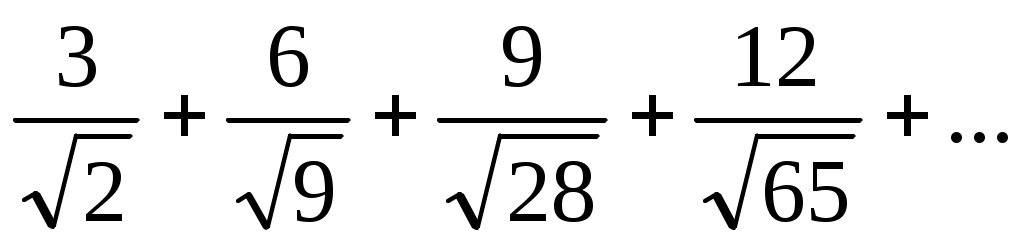
5)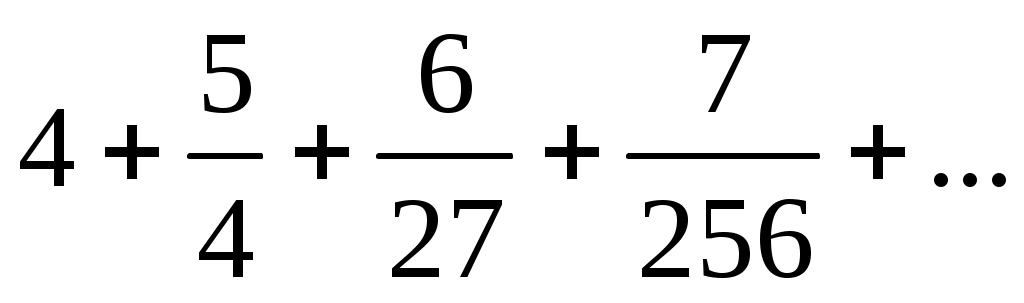
6)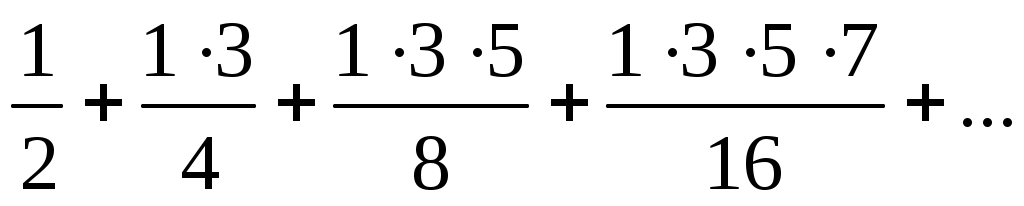
7)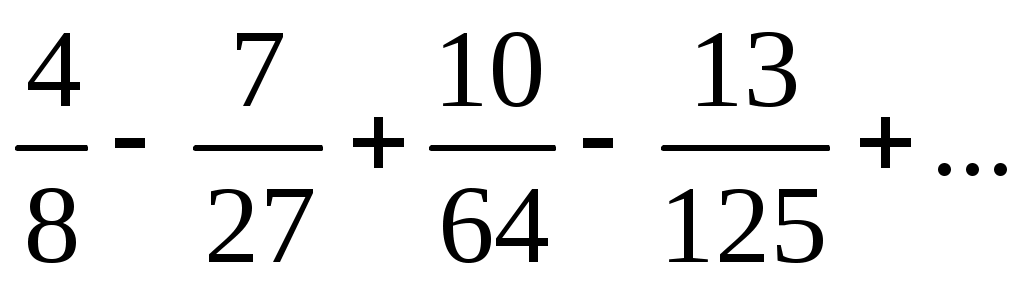
8)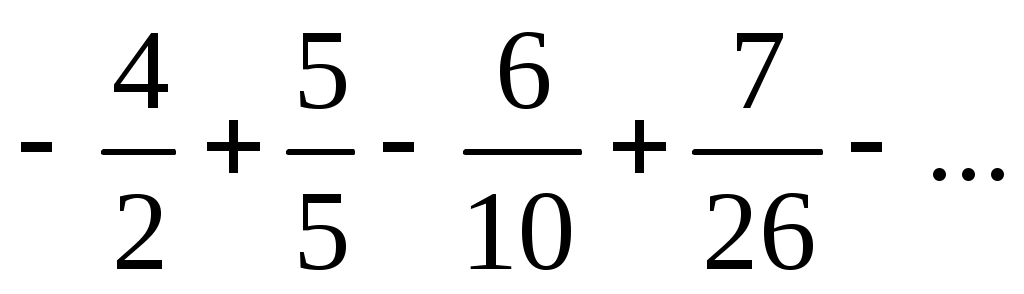
9)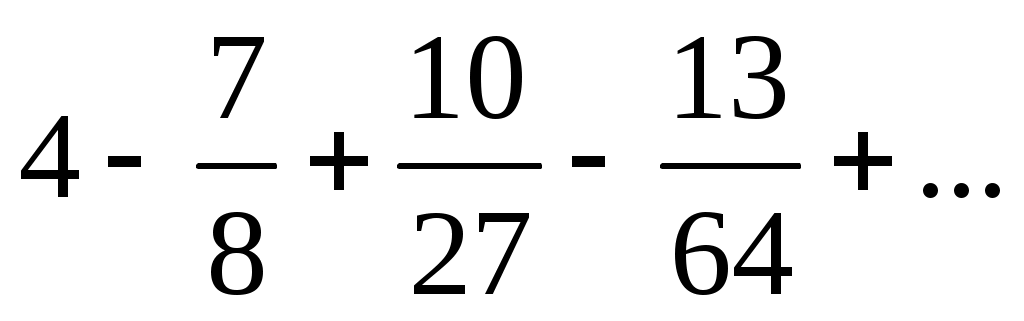
10)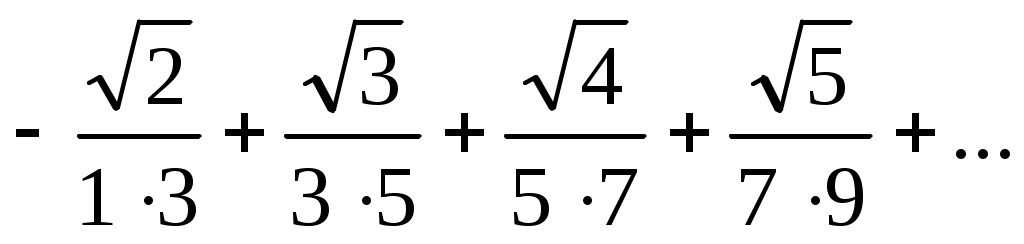
В задачах 11-16 написать 5 первых членов ряда
11)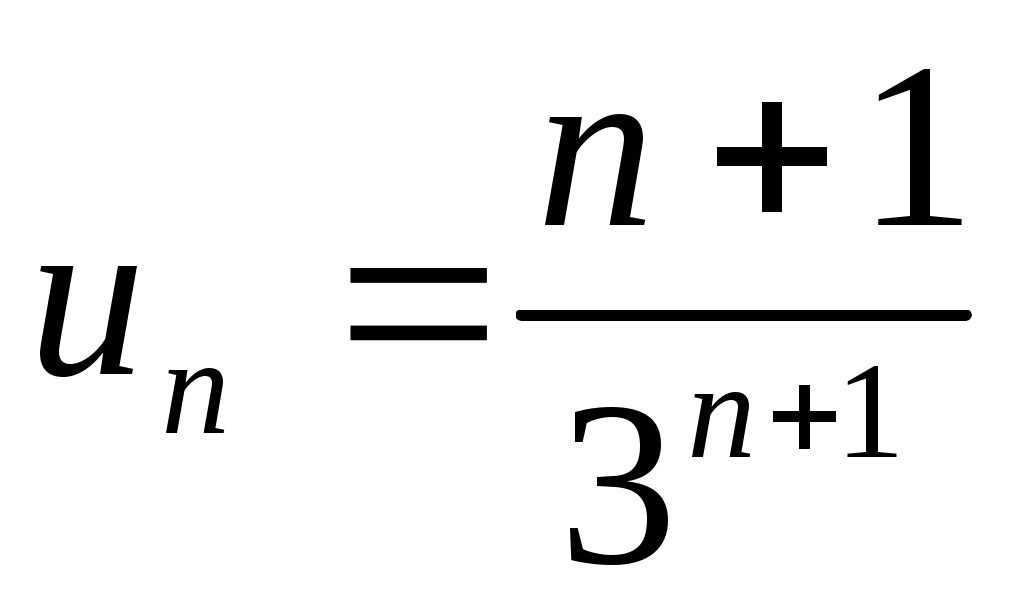 .
.
12)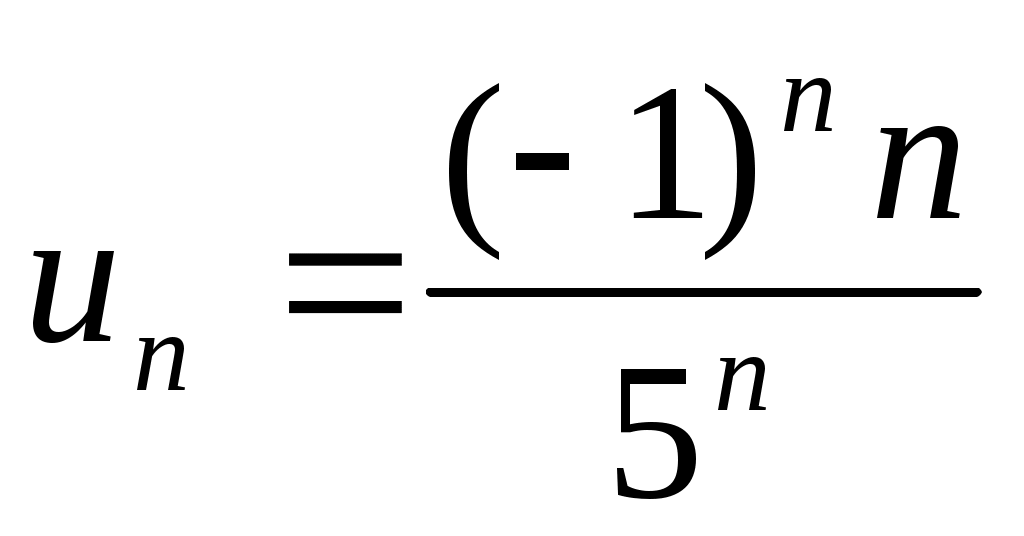 .
.
13)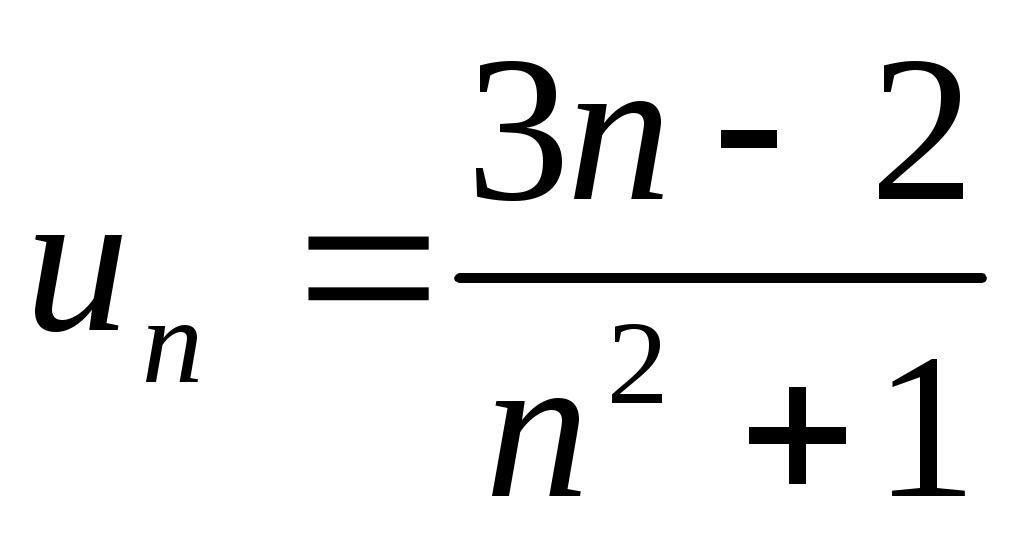 .
.
14)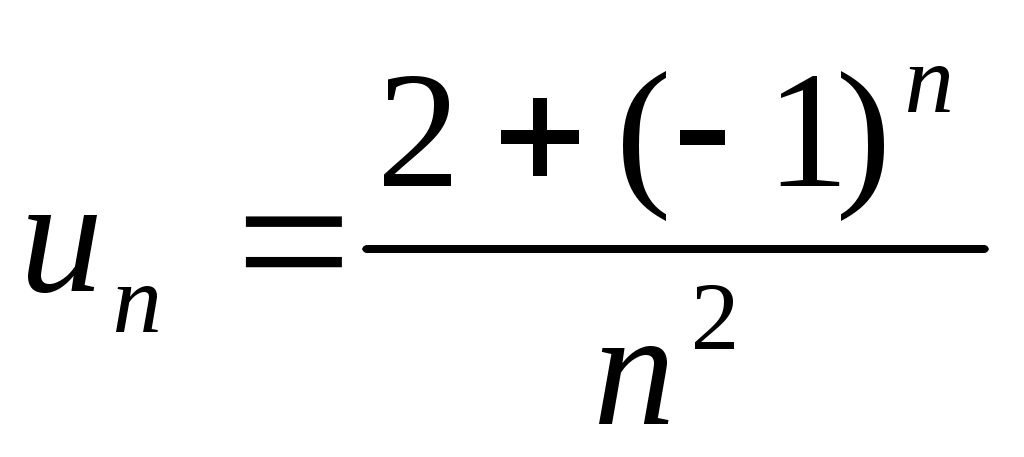 .
.
15)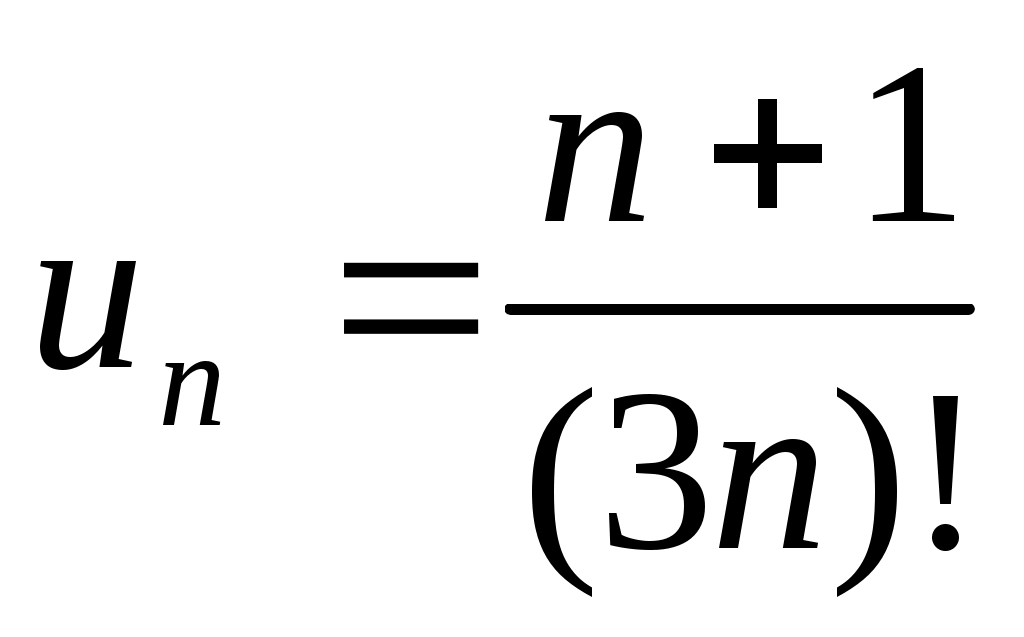 .
.
16)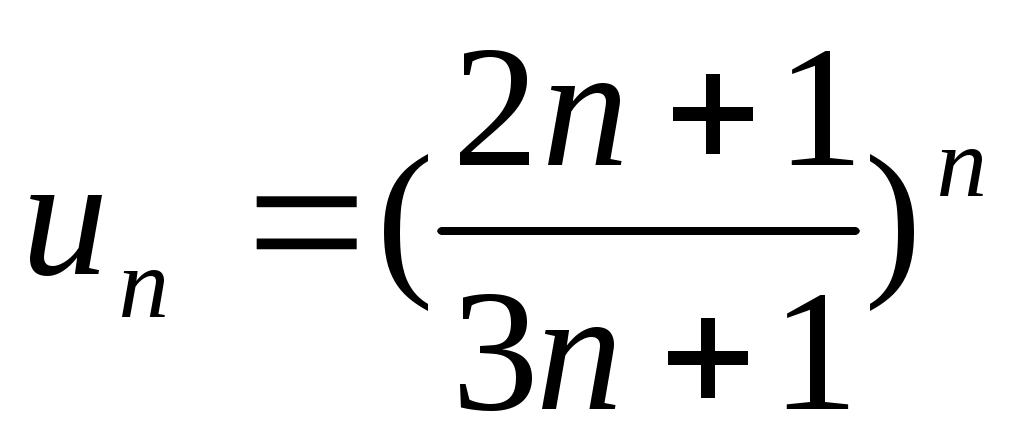 .
.
В задачах 17-24 1) найти сумму n первых членов ряда (Sn), 2) доказать сходимость ряда, пользуясь непосредственно определением сходимости и 3) найти сумму ряда (S):
17)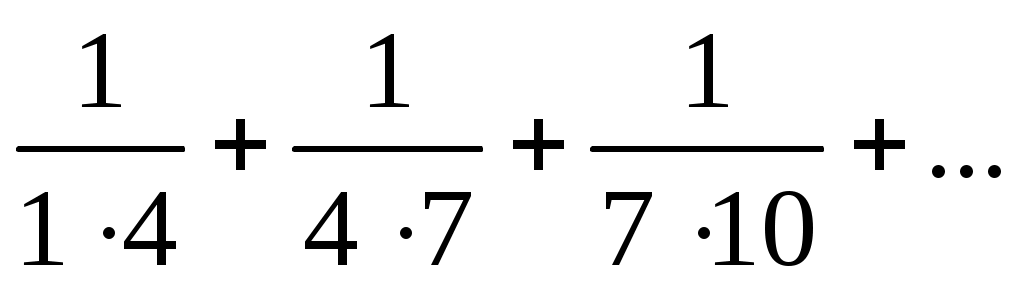
18)
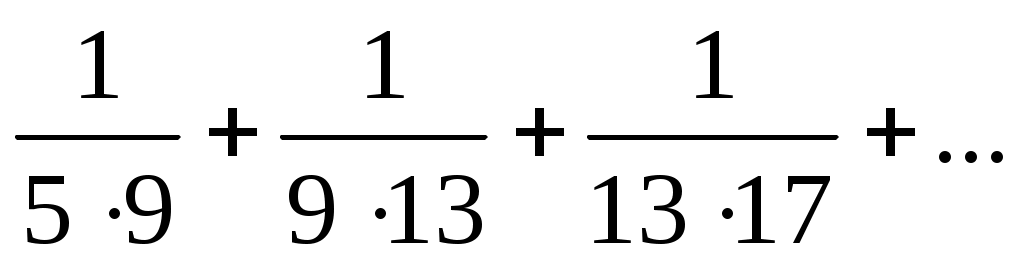
19)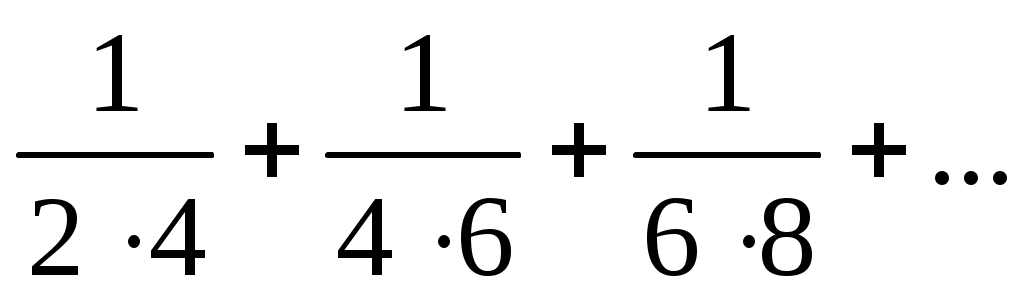
20)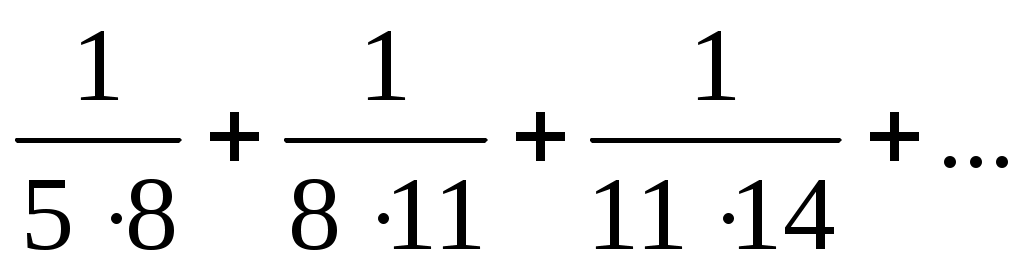
21)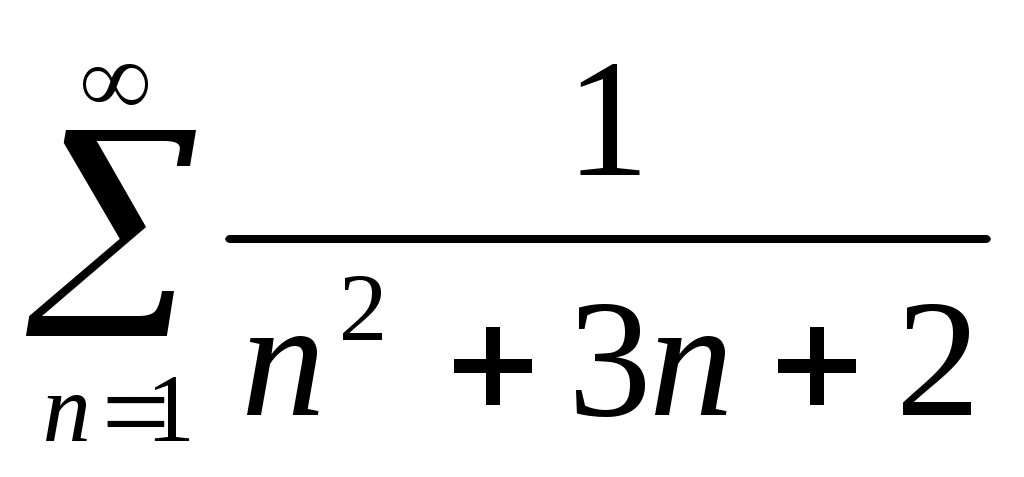 .
.
22)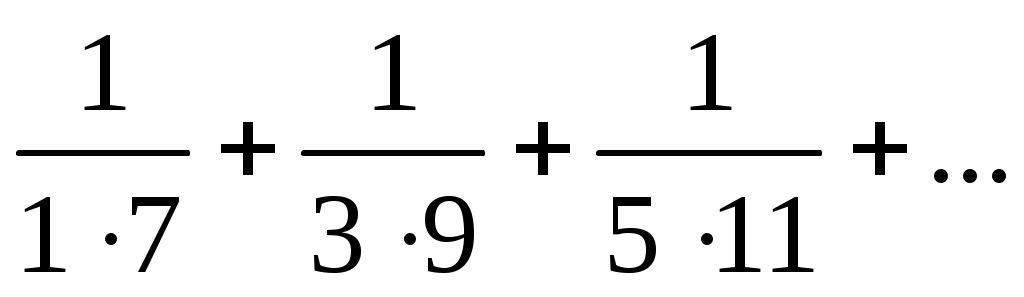
23)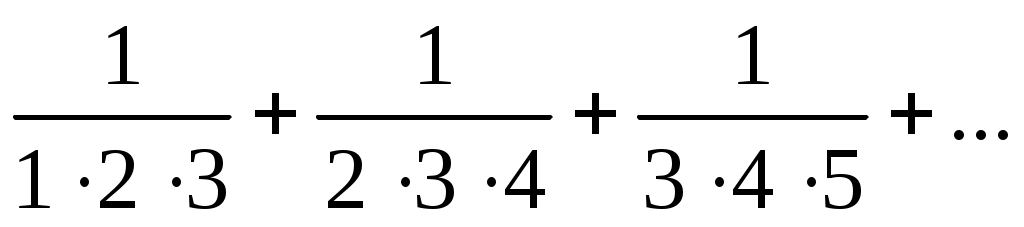
24)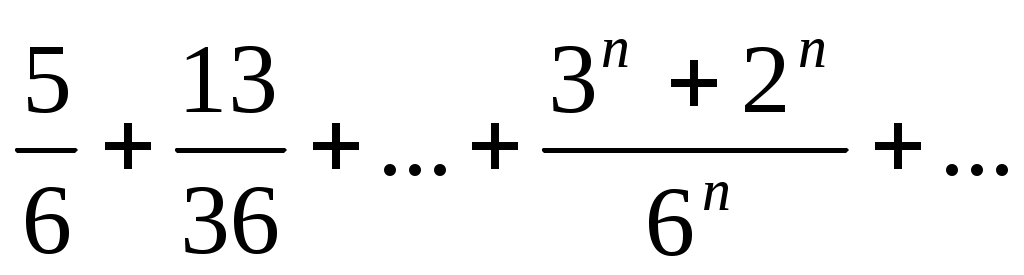
В задачах 25-30 выяснить, сходится ли данный ряд. Для сходящегося ряда найти его сумму:
25)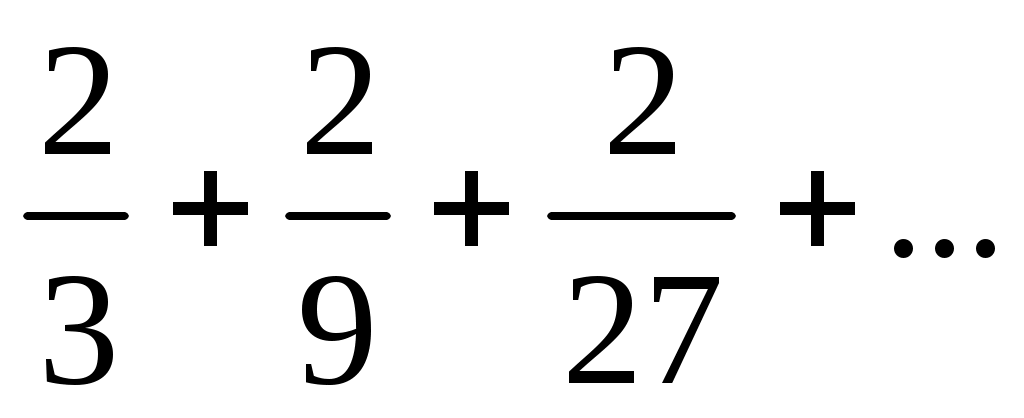
26)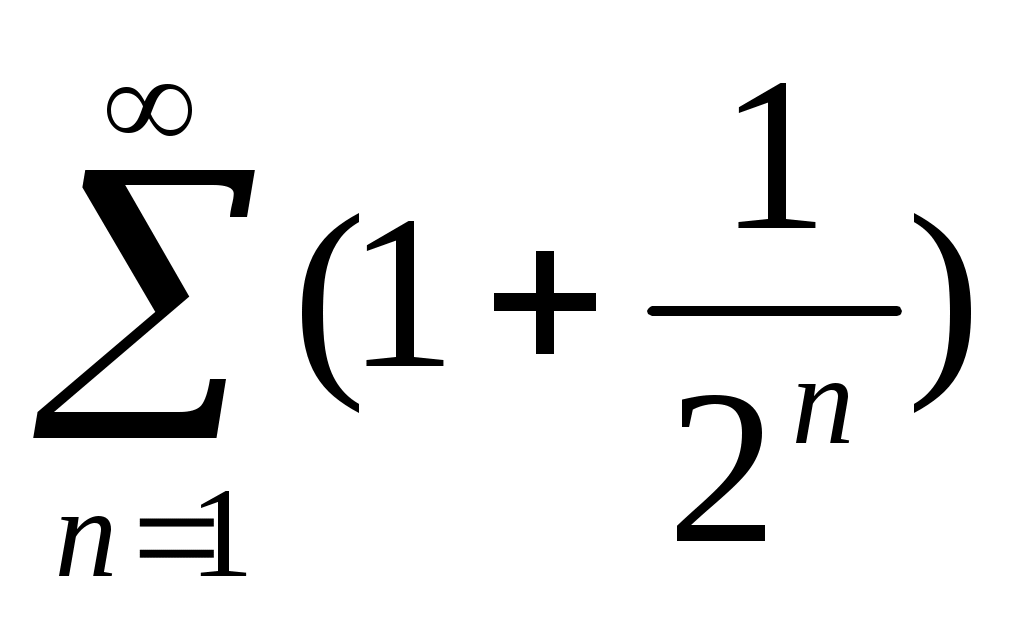 .
.
27)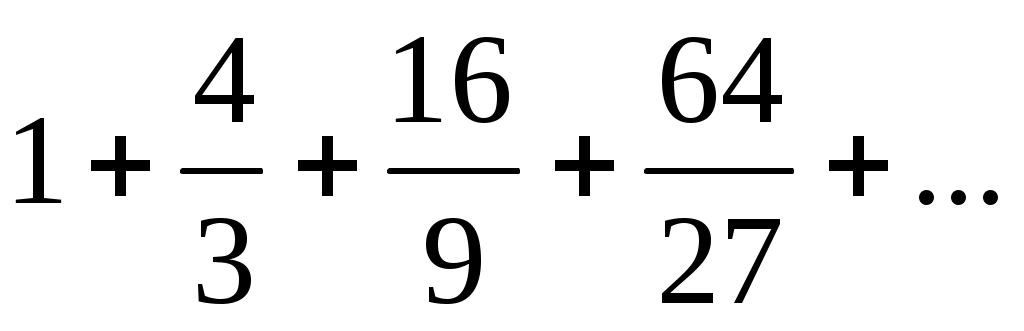
28)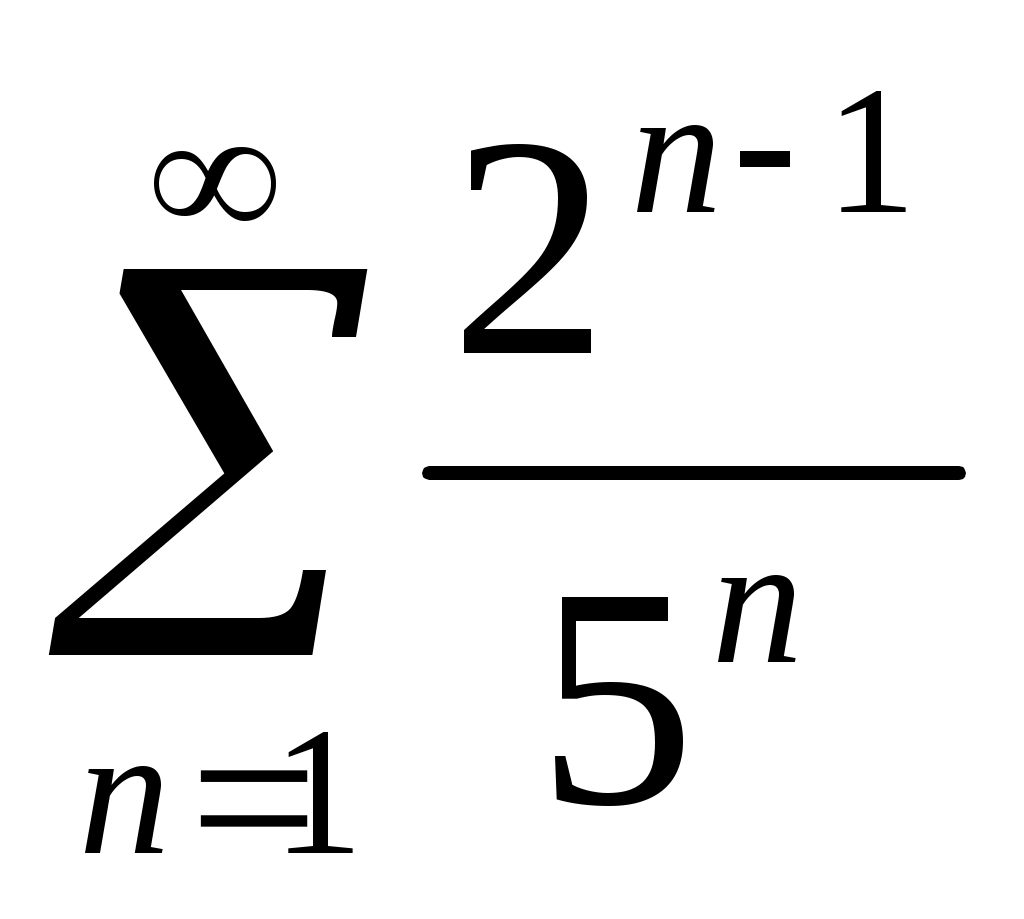 .
.
29)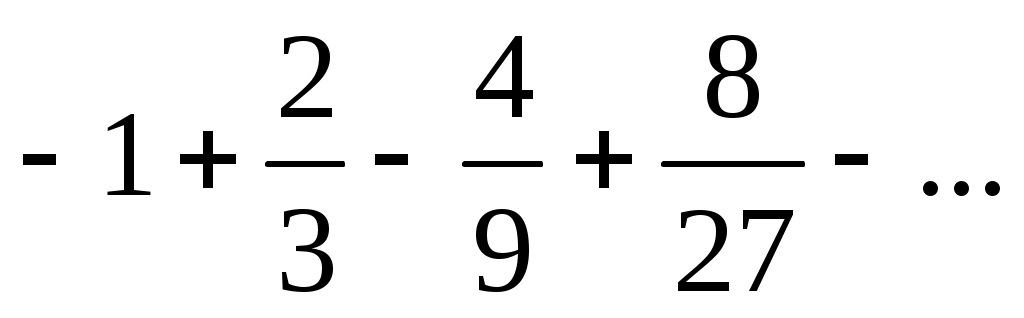
30)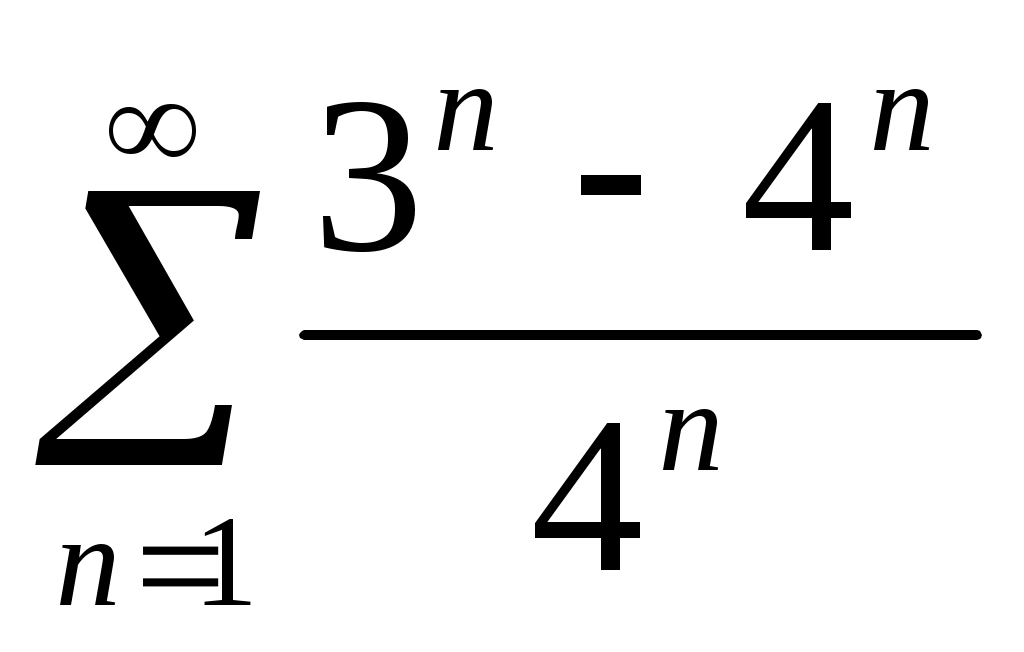 .
.
В задачах 31-45 исследовать сходимость рядов с помощью признаков сравнения и необходимого признака.
31)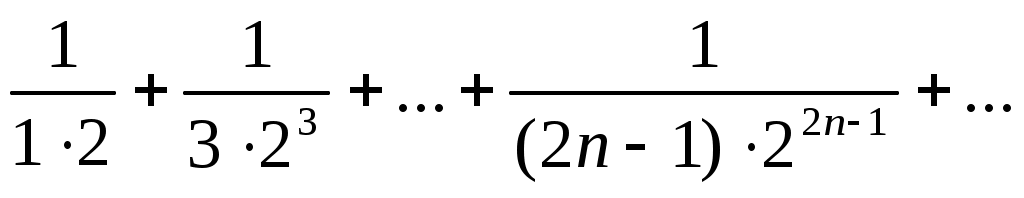
32)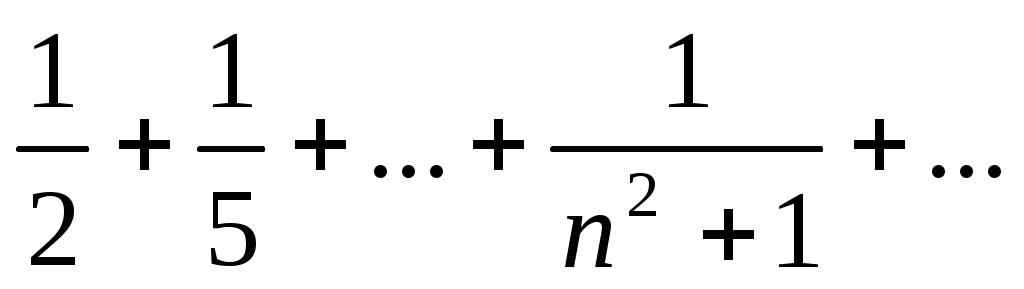
33)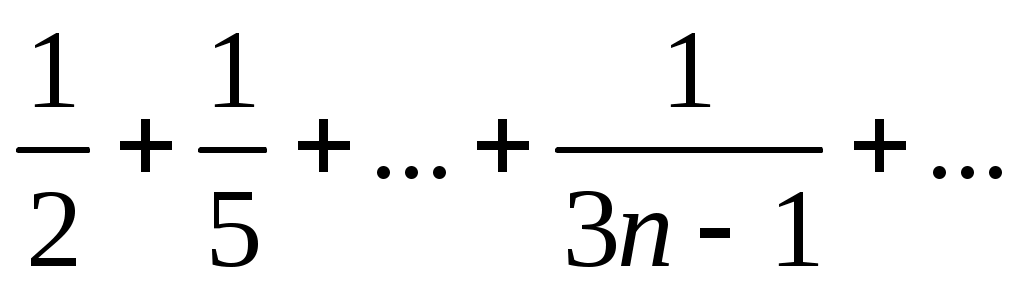
34)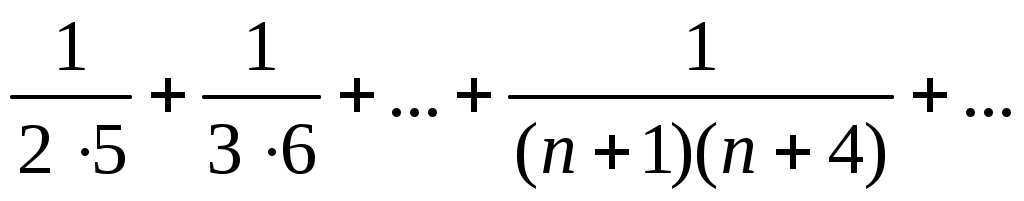
35)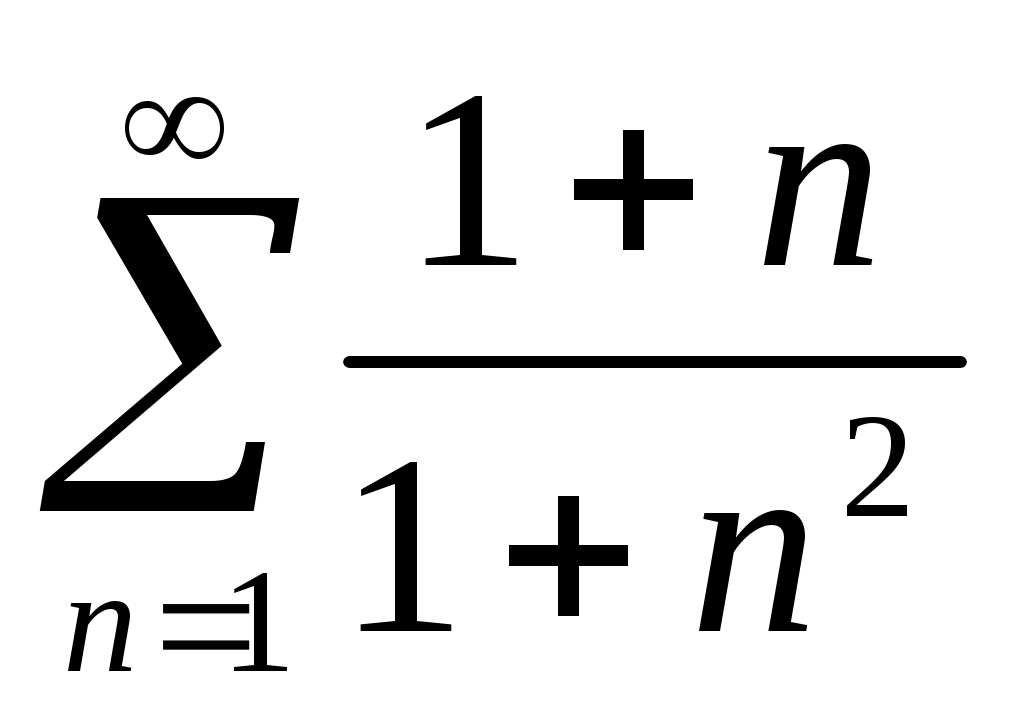
36)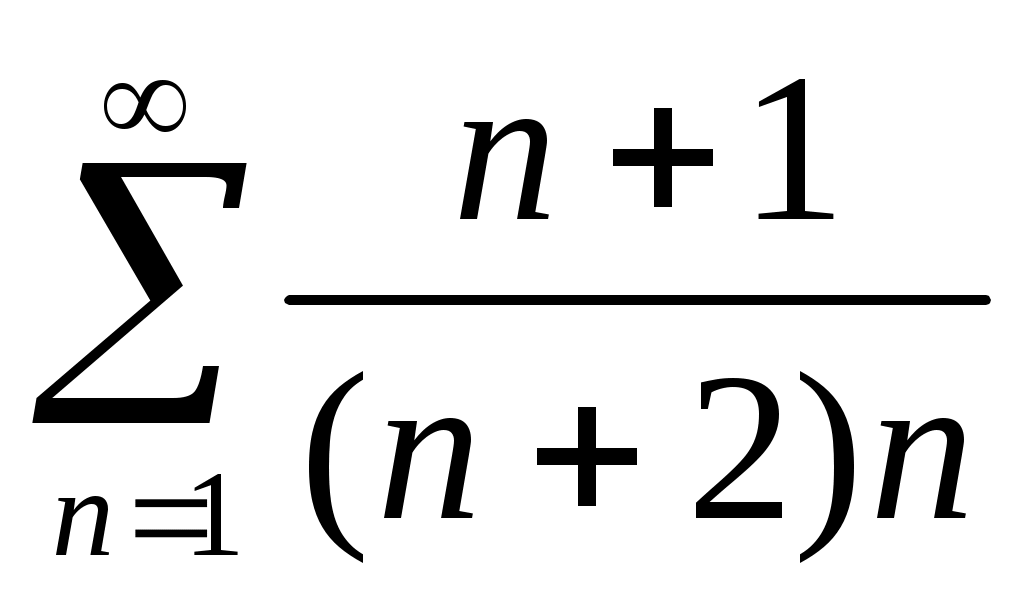
37)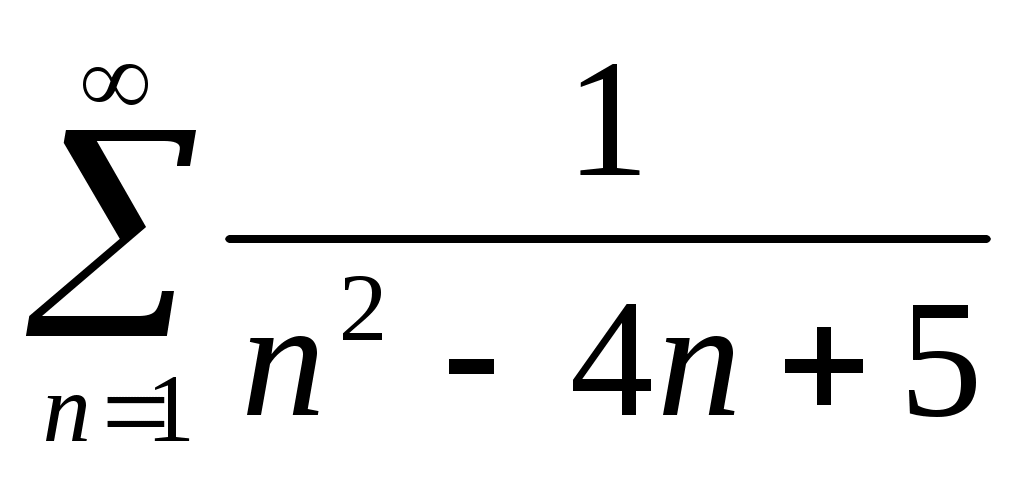
38)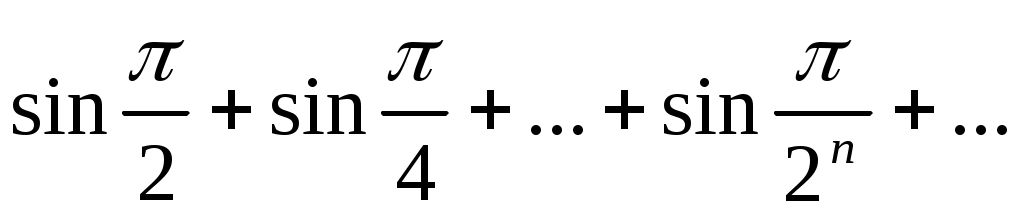
39)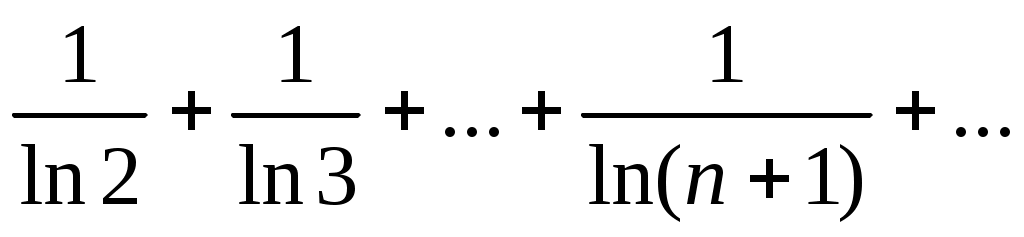
40)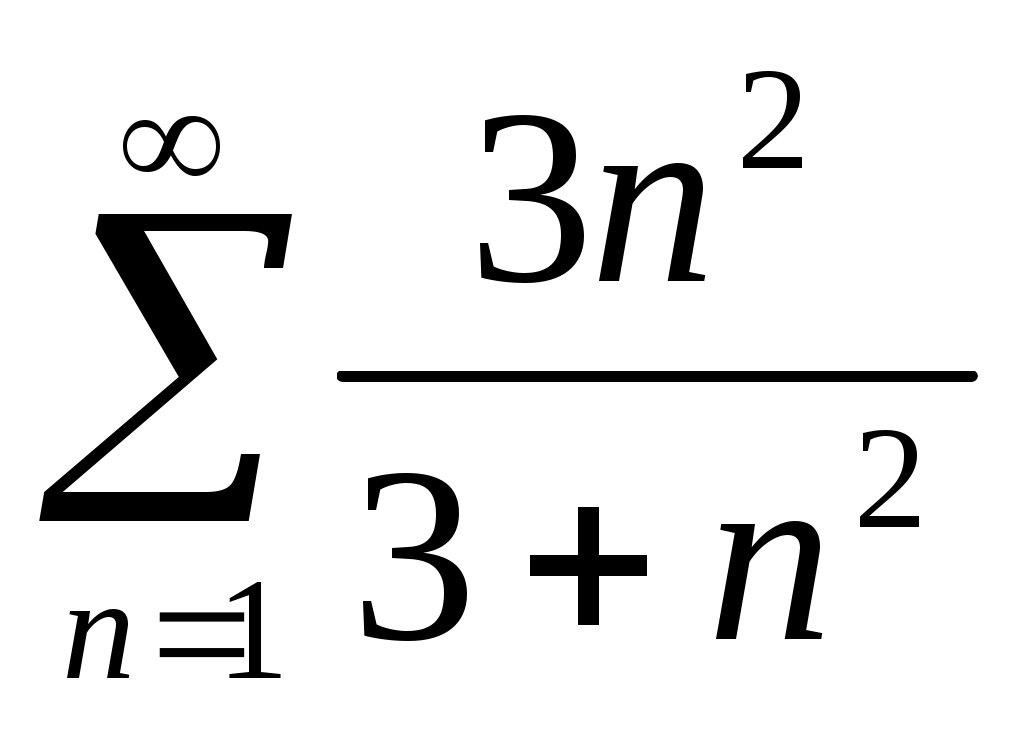
41)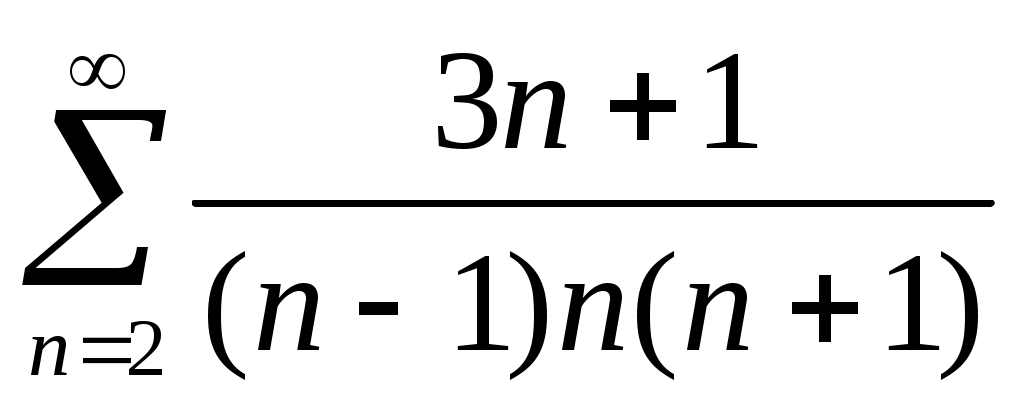
42)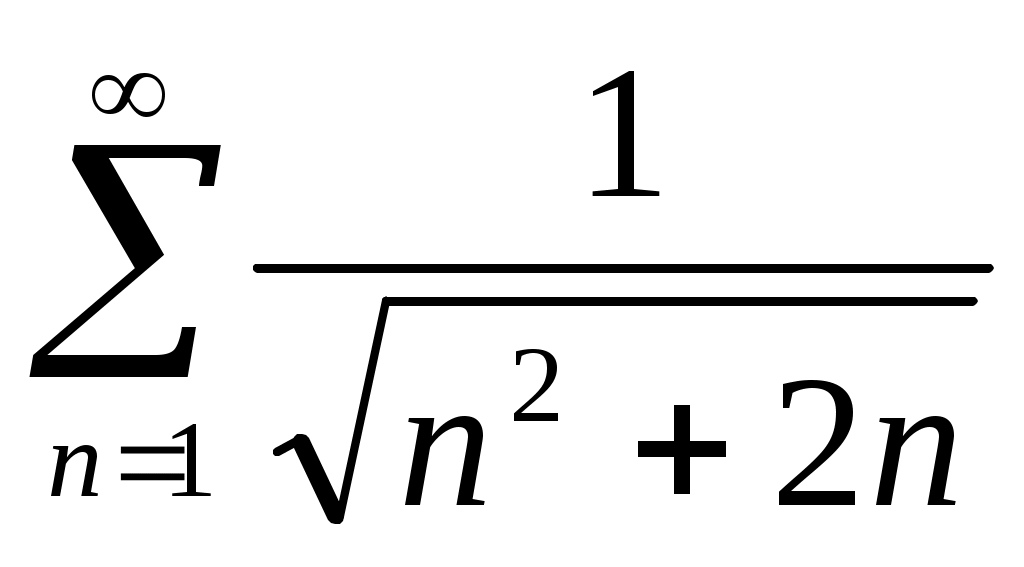
43)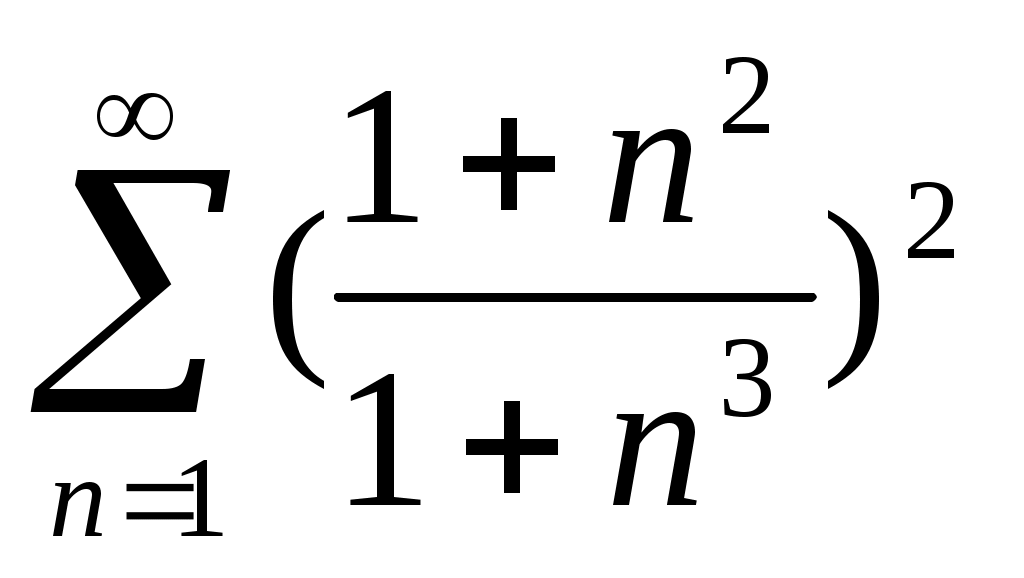
44)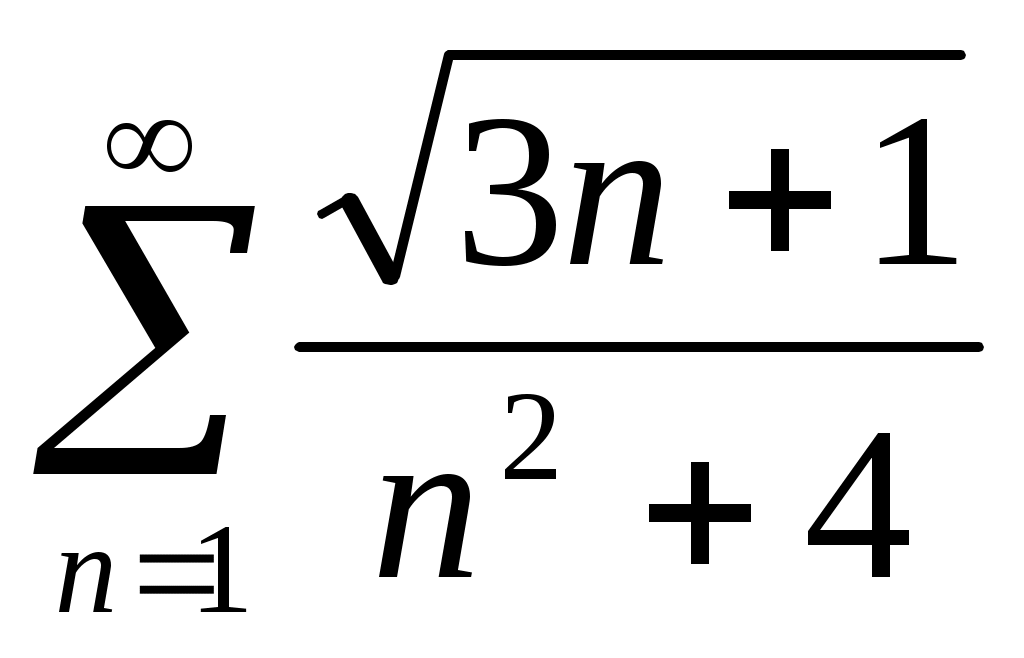
45)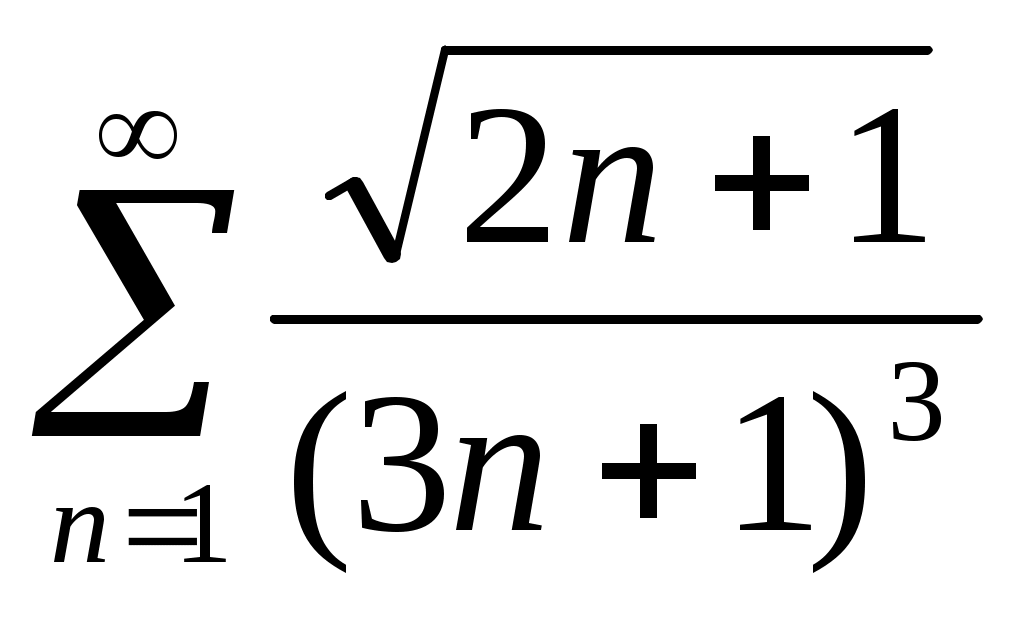
В задачах 46-58 исследовать сходимость рядов с помощью признака Даламбера:
46)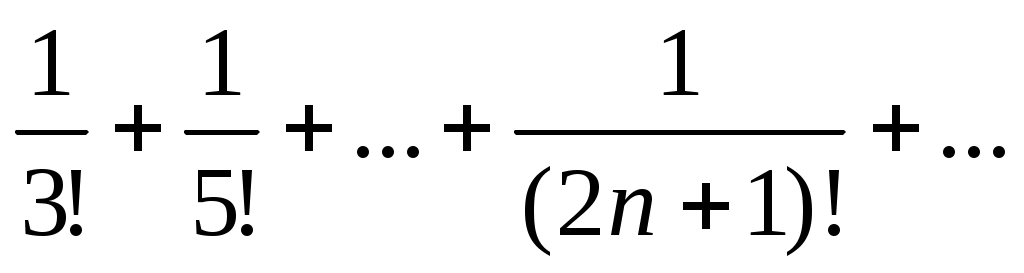
47)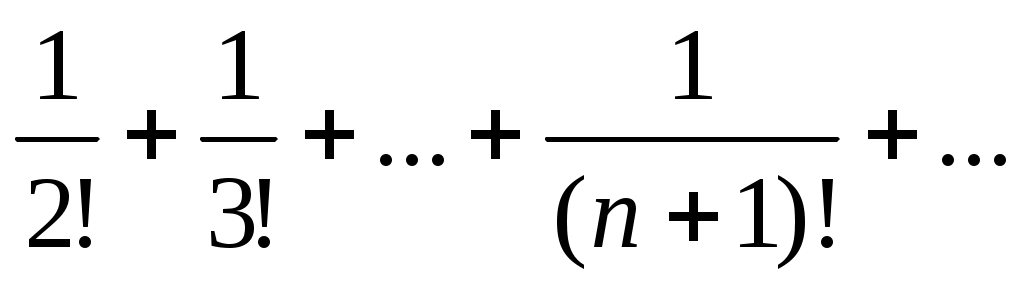
48)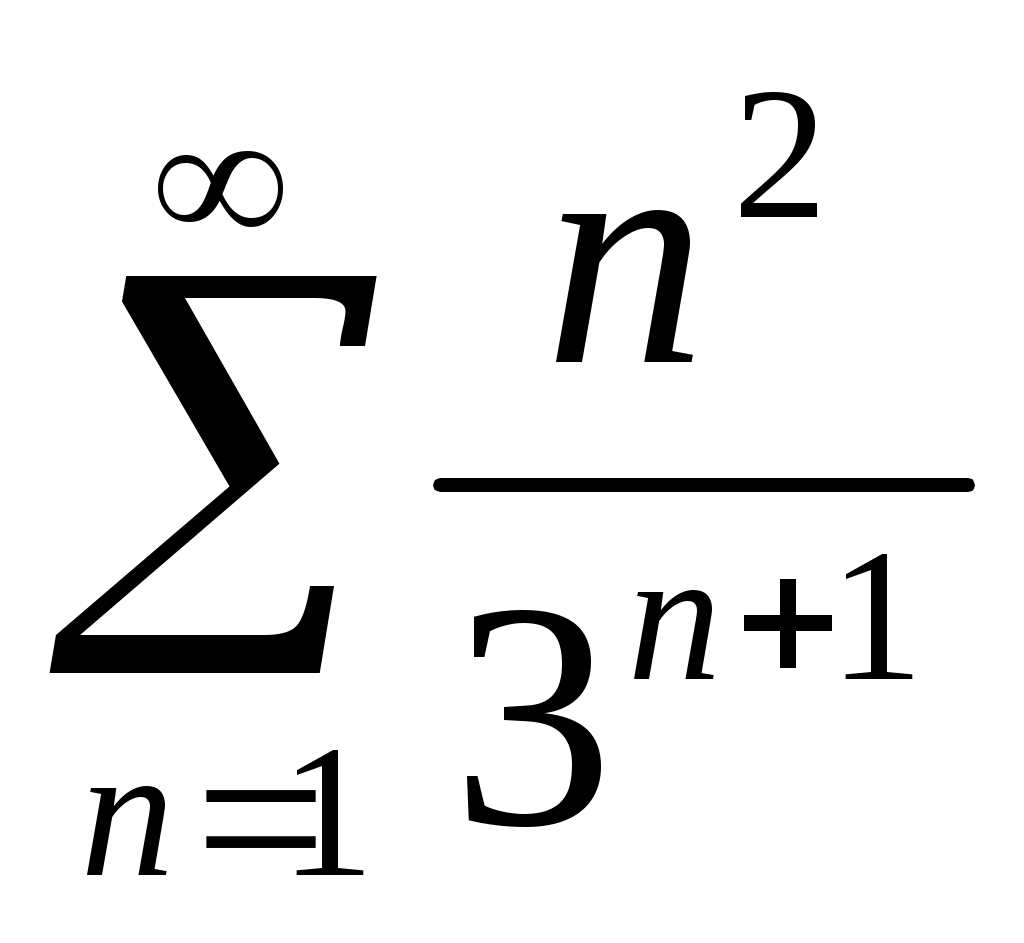 .
.
49)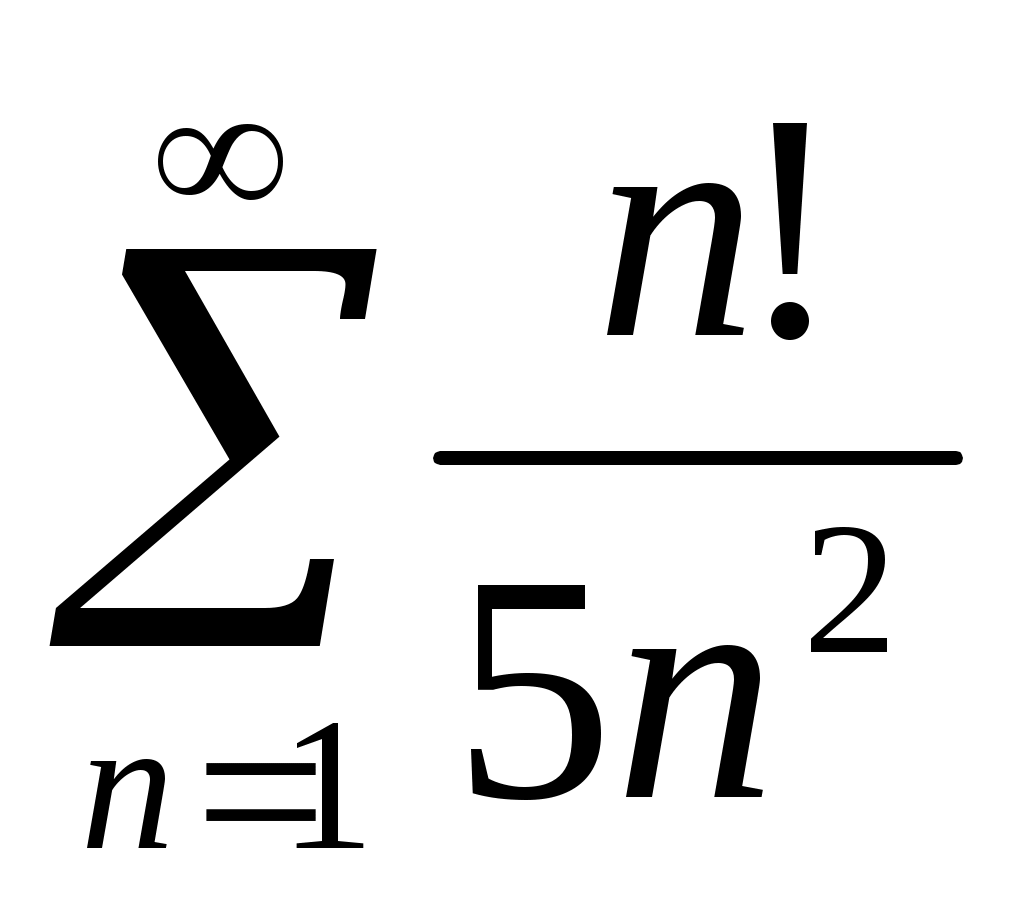 .
.
50)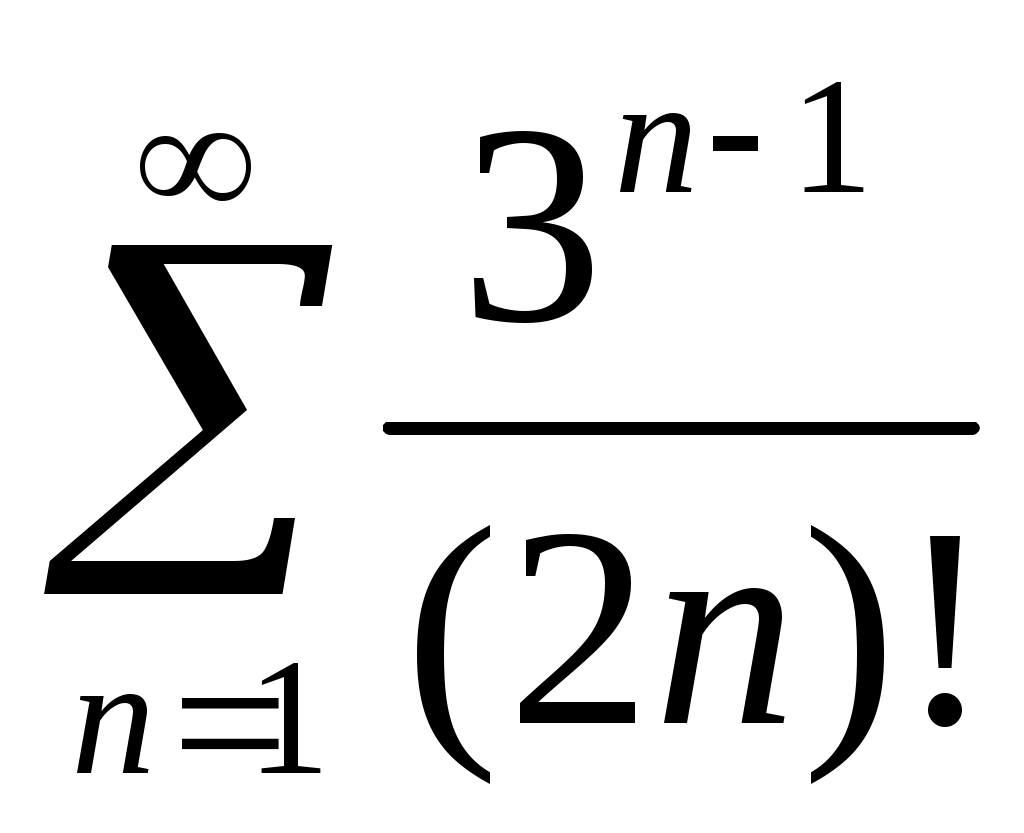 .
.
51)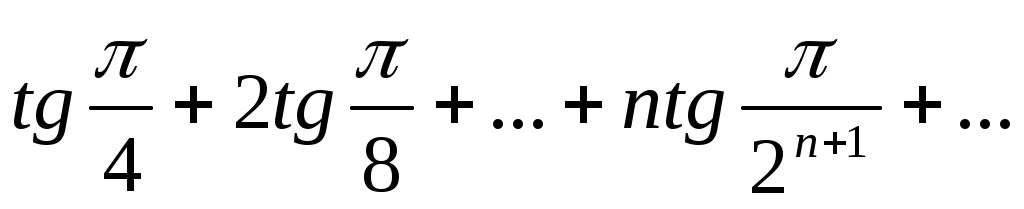
52)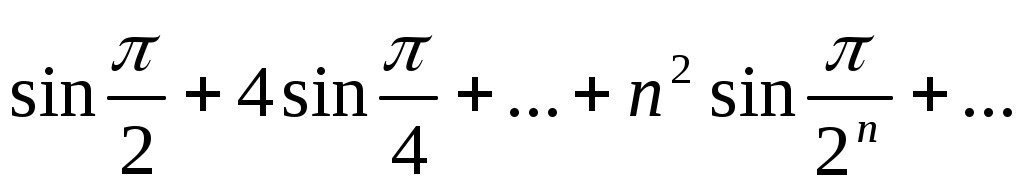
53)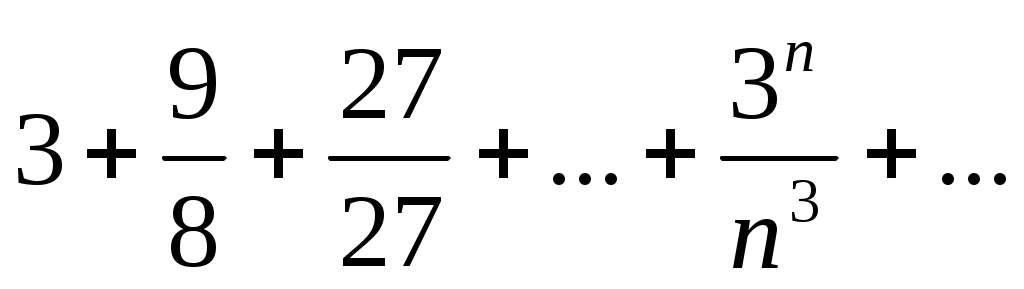 .
.
54)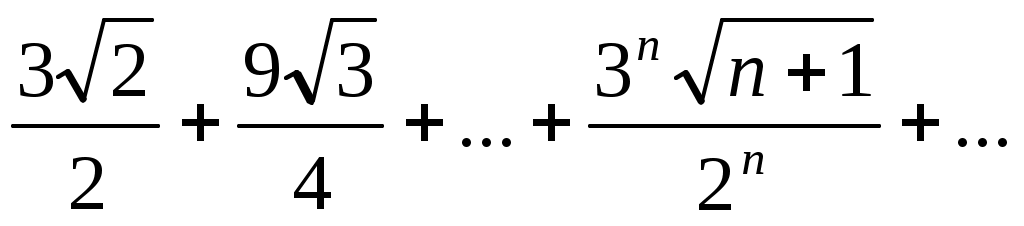 .
.
55)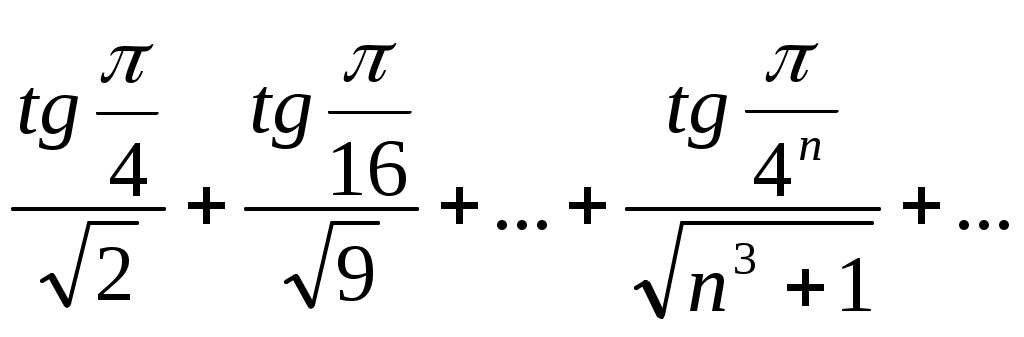
56)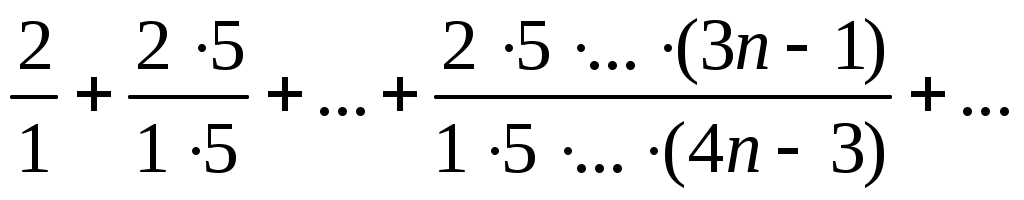
57)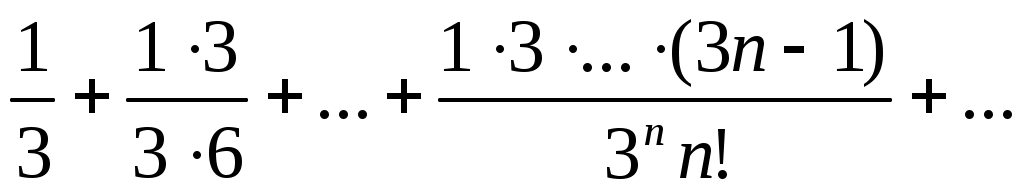
58)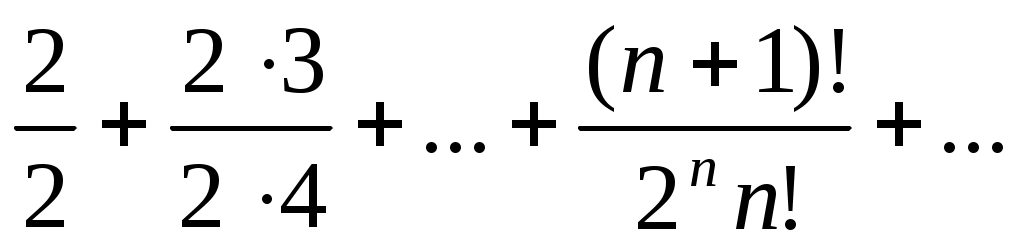
В заданиях 59-65 вопрос о сходимости рядов решить с помощью интегрального признака Коши:
59)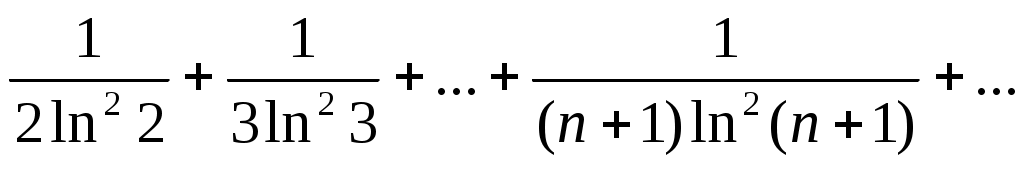
60)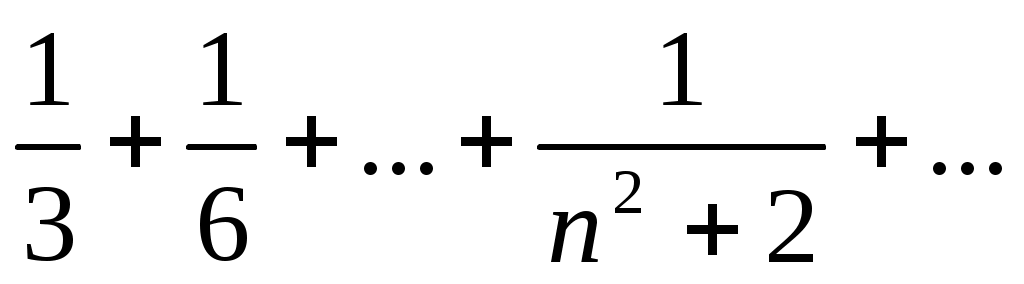
61)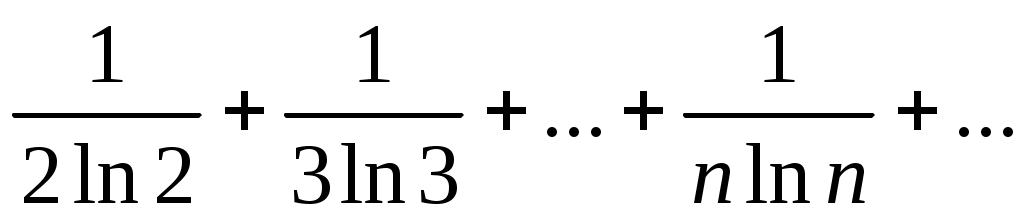
62)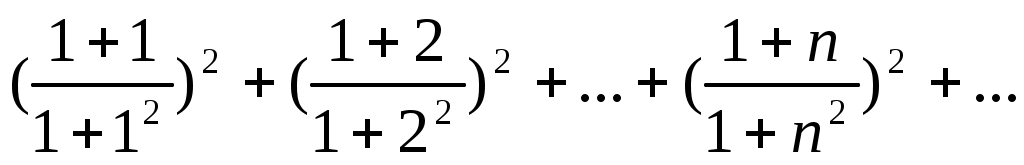
63)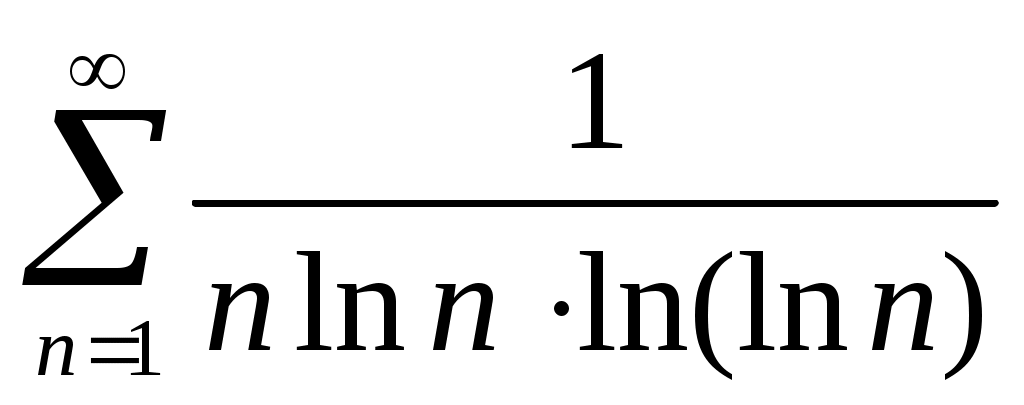 .
.
64)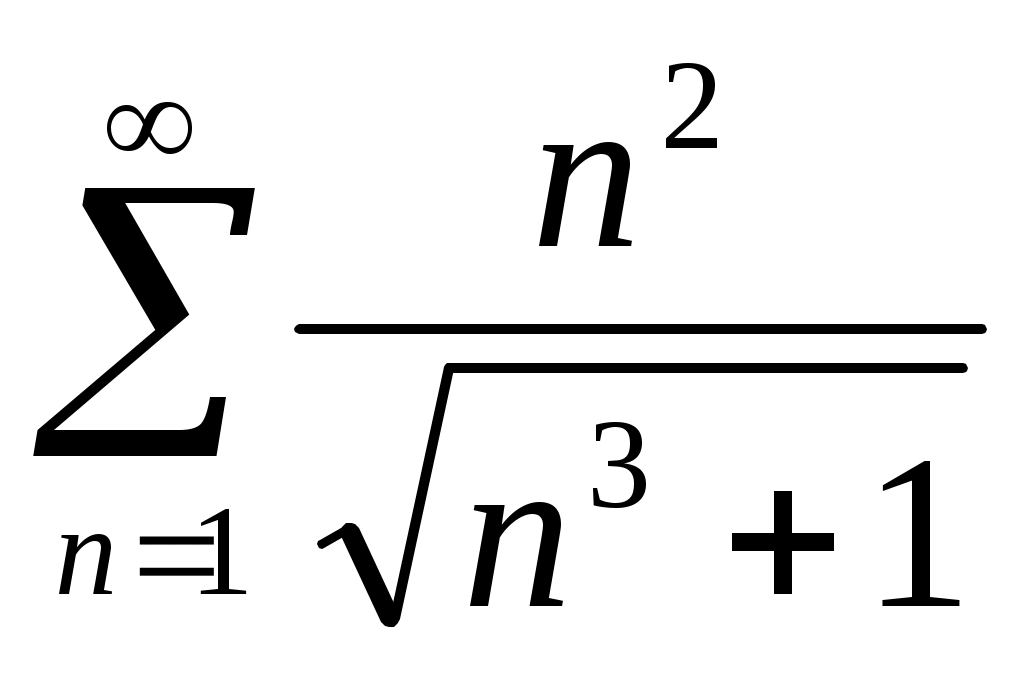 .
.
65)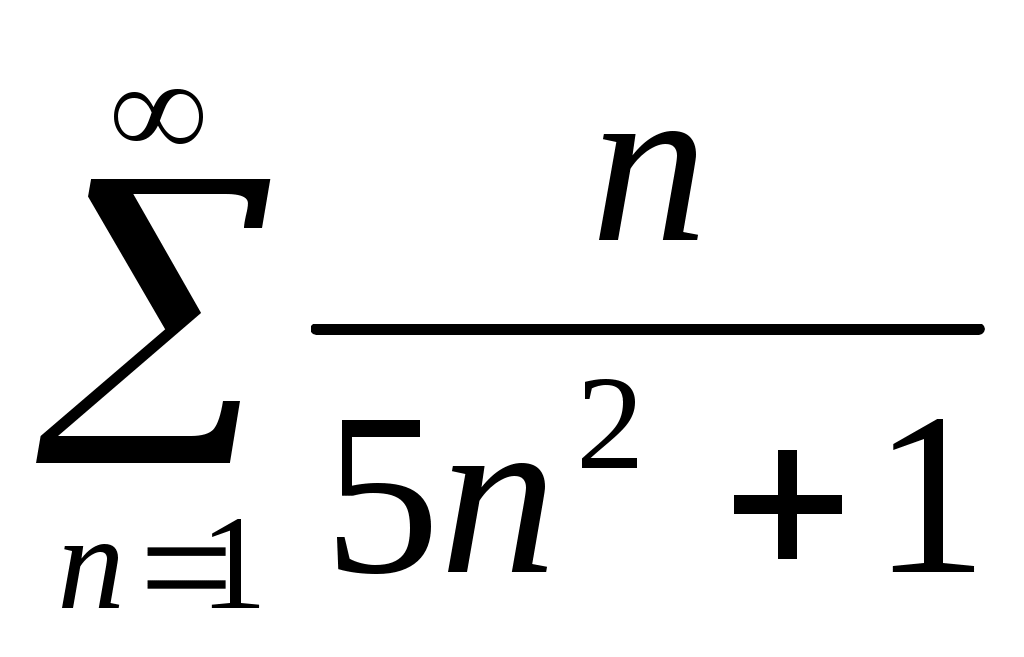 .
.
В задачах 66-72 исследовать сходимость рядов с помощью радикального признака Коши:
66)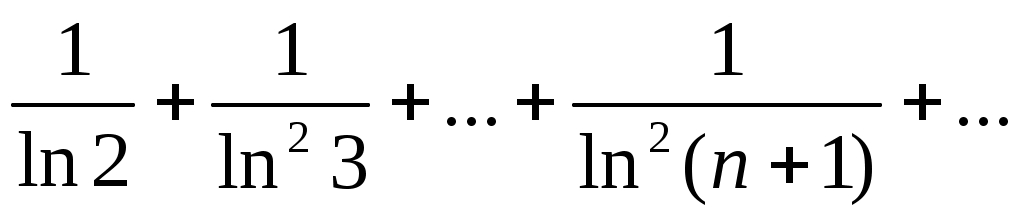
1) Рядом сравнения будет гармонический ряд
следовательно, ряды ведут себя одинаково, а т.к. гармонический ряд расходится, то и данный ряд также расходится.
2) В качестве ряда сравнения выберем обобщенный гармонический ряд
(
Из примеров следует вывод:
Чтобы выбрать ряд сравнения, нужно разделить старшую степень числителя на старшую степень знаменателя; образовавшийся после сокращения обобщенный гармонический ряд и есть ряд сравнения.
2. Признак Даламбера.
Если для знакоположительного ряда
то при 1) L<1 ряд сходится; 2) L>1 ряд расходится; 3) L=1 признак ответа не дает.
Признак Даламбера обычно применяется в том случае, когда общий член ряда содержит факториалы, показательную функцию от n, синус или тангенс бесконечно малого аргумента.
Пример. Исследовать на сходимость:
1)
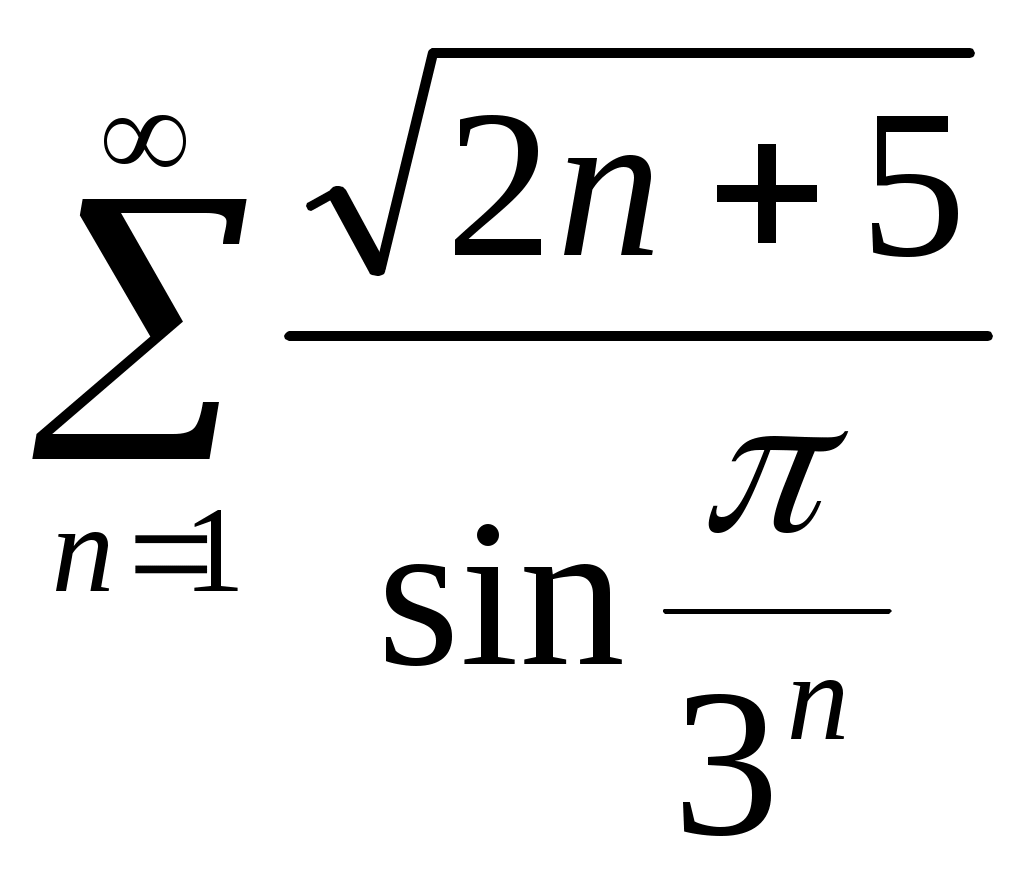 , 2)
, 2) 1) Т.к.
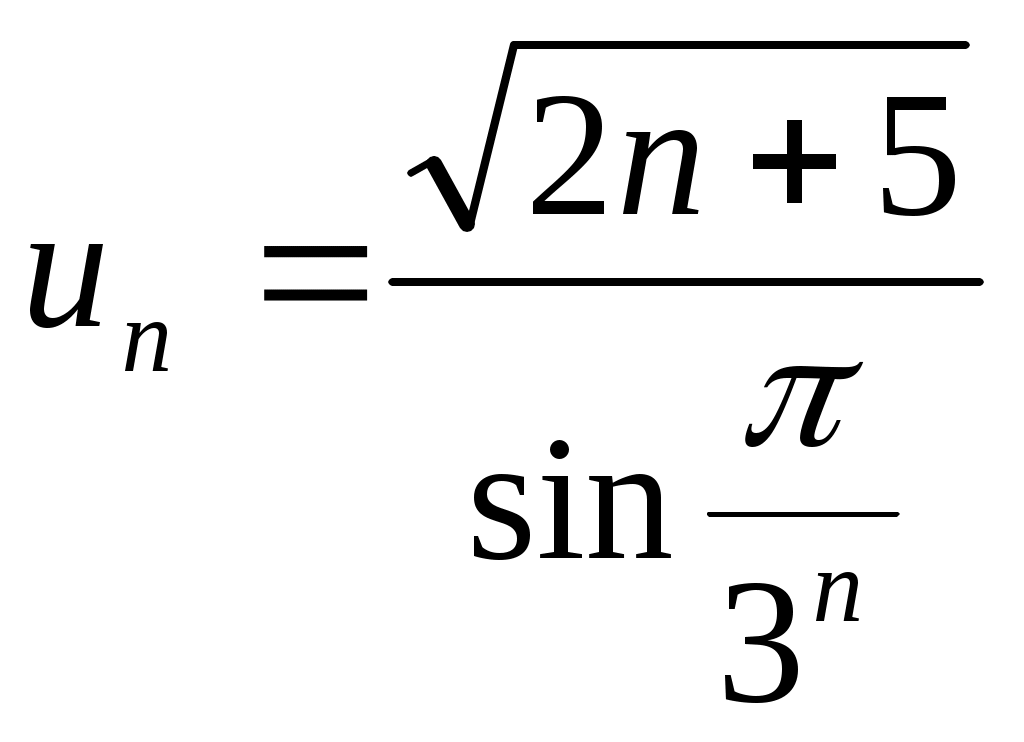 , то
, то 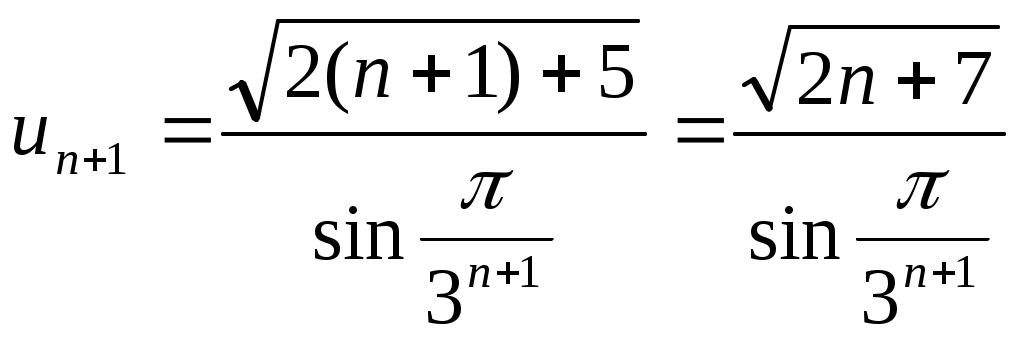
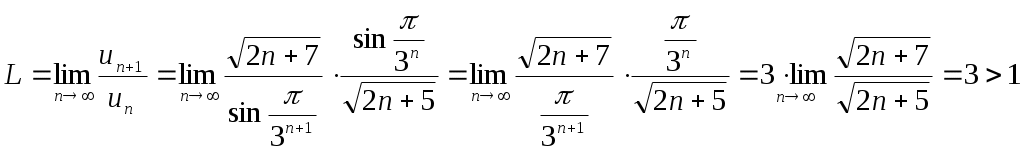 - ряд расходится.
- ряд расходится.2)
;
3. Интегральный признак Коши.
Пусть члены ряда u1, u2, u3,..., un,... положительны и не возрастают, т.е.
u1 ≥u2≥ u3≥...
и пусть
f(1)=u1; f(2)=u2;...; f(n)=un
Тогда:
-
если несобственный интеграл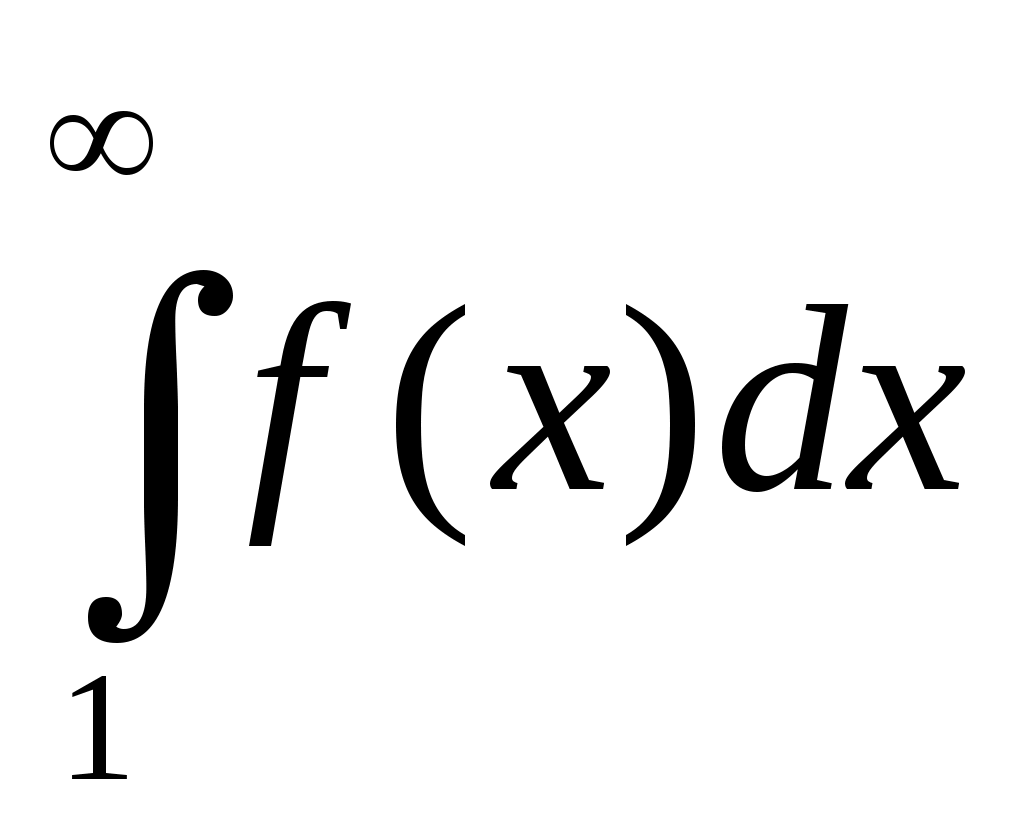 сходится, то и ряд сходится;
сходится, то и ряд сходится; -
если же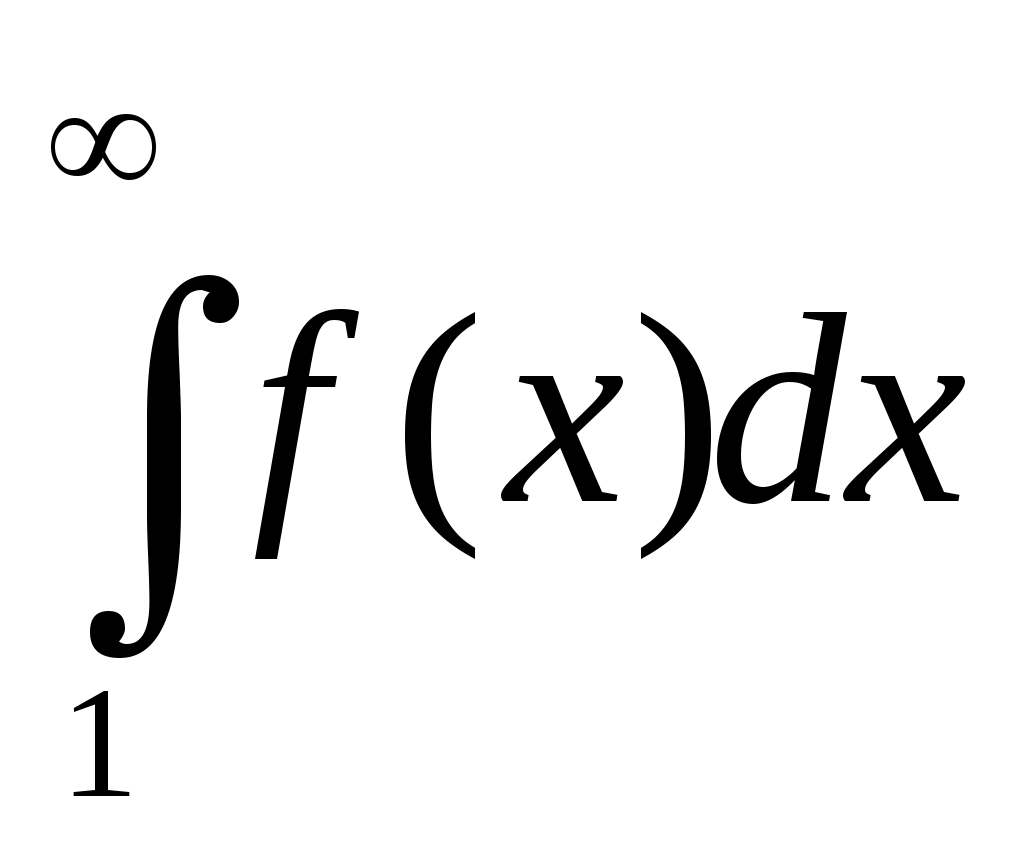 расходится, то и ряд расходится.
расходится, то и ряд расходится.
Пример. Исследовать на сходимость:
-
Заменяем в заданном выражении общего члена ряда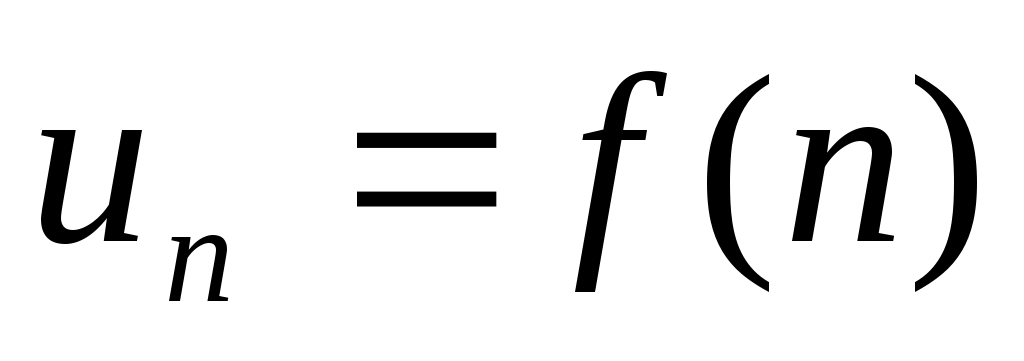 номер n непрерывной переменной x и убеждаемся, что полученная функция
номер n непрерывной переменной x и убеждаемся, что полученная функция
является непрерывной и убывающей на всем бесконечном интервале изменения x. Затем находим несобственный интеграл от
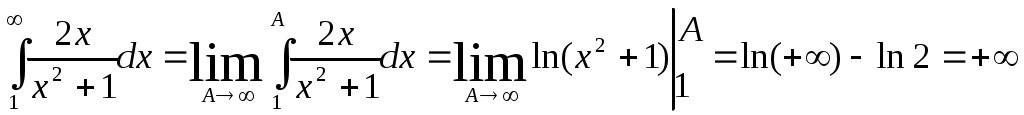
Несобственный интеграл расходится, следовательно, и данный ряд также расходится.
2)
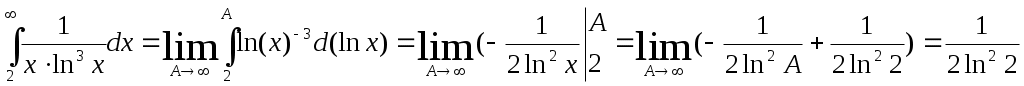
Несобственный интеграл сходится, следовательно, и рассматриваемый ряд также сходится.
4. Радикальный признак Коши.
Если для знакоположительного ряда
то при l<1 ряд сходится, а при l>1 расходится; при l=1 признак ответа не дает.
Пример. Исследовать на сходимость:
1)
; 2)
Решение:
Следовательно, исходный ряд расходится.
2)
следовательно, рассмотренный ряд является сходящимся.
Задачи для решения.
В задачах 1-10 написать формулу n-ого члена ряда.
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
В задачах 11-16 написать 5 первых членов ряда
11)
12)
13)
14)
15)
16)
В задачах 17-24 1) найти сумму n первых членов ряда (Sn), 2) доказать сходимость ряда, пользуясь непосредственно определением сходимости и 3) найти сумму ряда (S):
17)
18)
19)
20)
21)
22)
23)
24)
В задачах 25-30 выяснить, сходится ли данный ряд. Для сходящегося ряда найти его сумму:
25)
26)
27)
28)
29)
30)
В задачах 31-45 исследовать сходимость рядов с помощью признаков сравнения и необходимого признака.
31)
32)
33)
34)
35)
36)
37)
38)
39)
40)
41)
42)
43)
44)
45)
В задачах 46-58 исследовать сходимость рядов с помощью признака Даламбера:
46)
47)
48)
49)
50)
51)
52)
53)
54)
55)
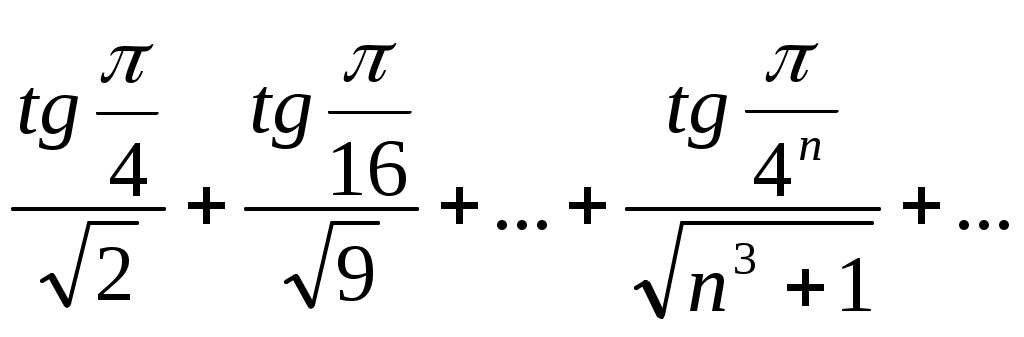
56)
57)
58)
В заданиях 59-65 вопрос о сходимости рядов решить с помощью интегрального признака Коши:
59)
60)
61)
62)
63)
64)
65)
В задачах 66-72 исследовать сходимость рядов с помощью радикального признака Коши:
66)