Исследуем соответствующий остаточный член формулы Тейлора:



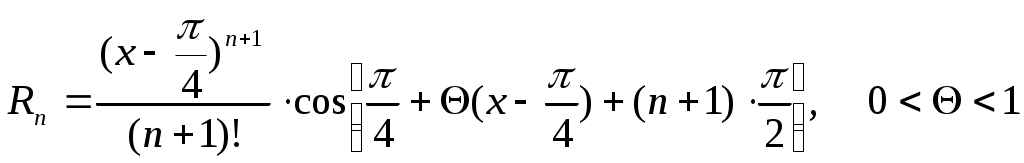
Каково бы ни было значение , всегда найдутся такие два последовательных положительных числа и , между которыми заключается , т.е. . Исходя из этого, получим очевидное неравенство:



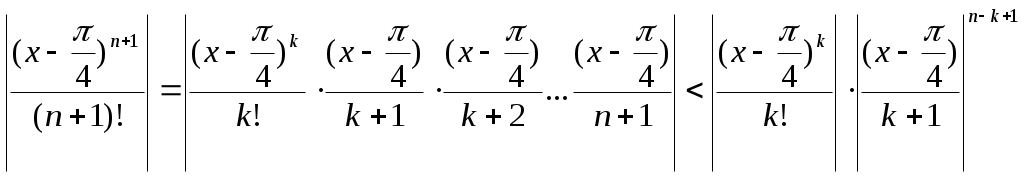
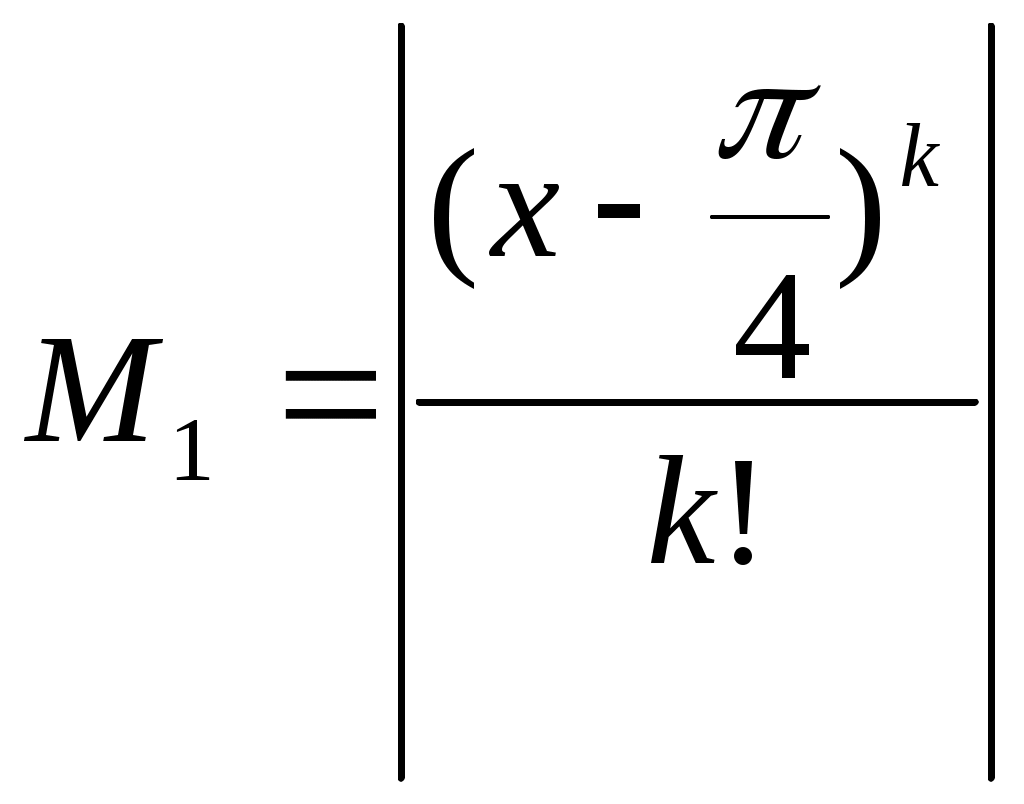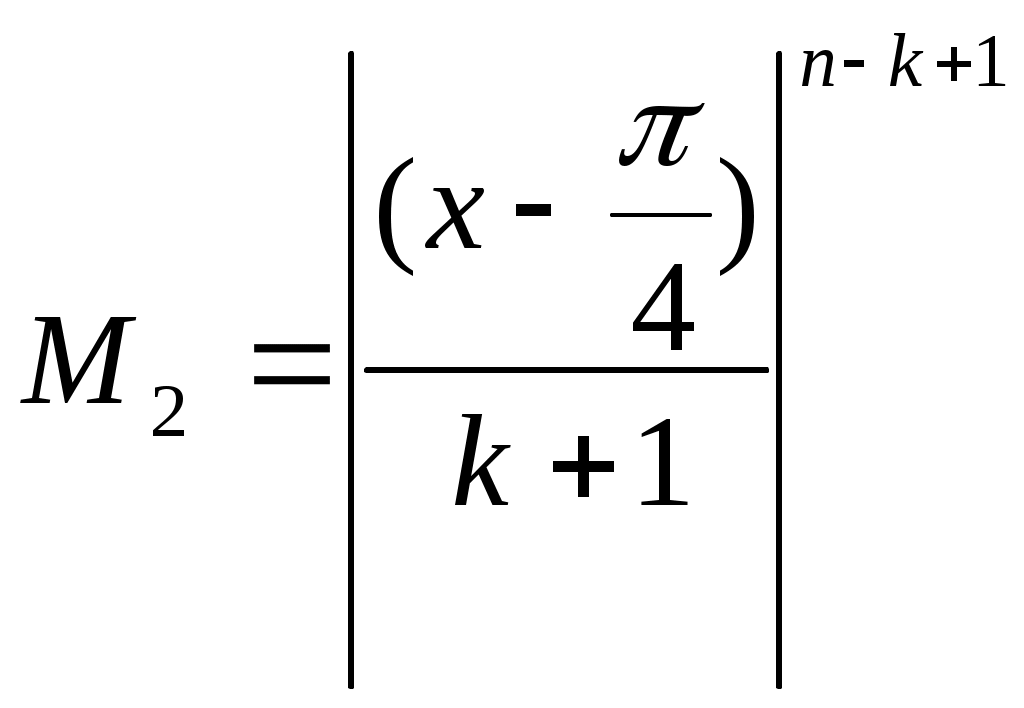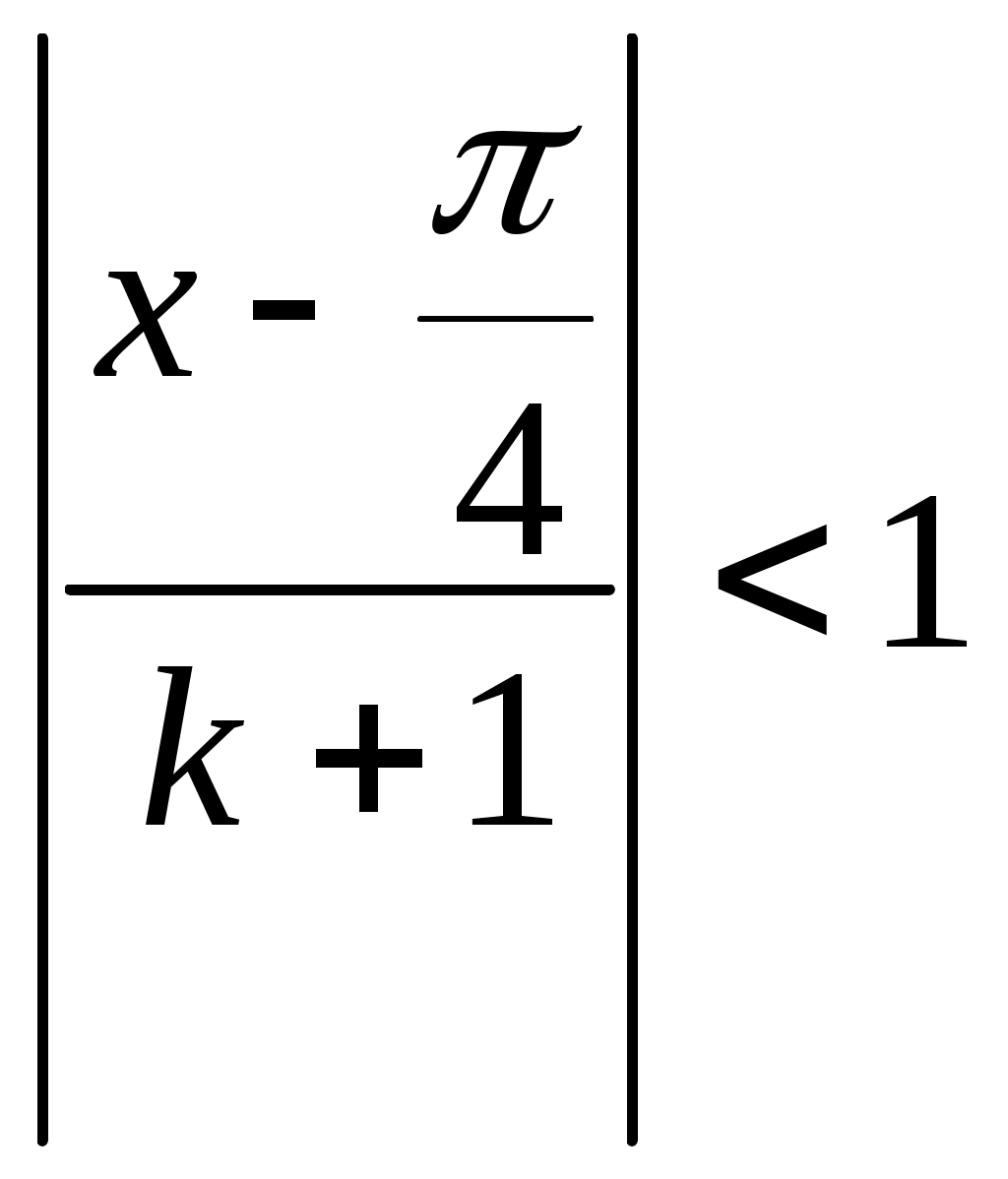Первый множитель не зависит от и при любом данном значении является постоянным; второй множитель при будет величиной бесконечно малой, ибо . Следовательно, 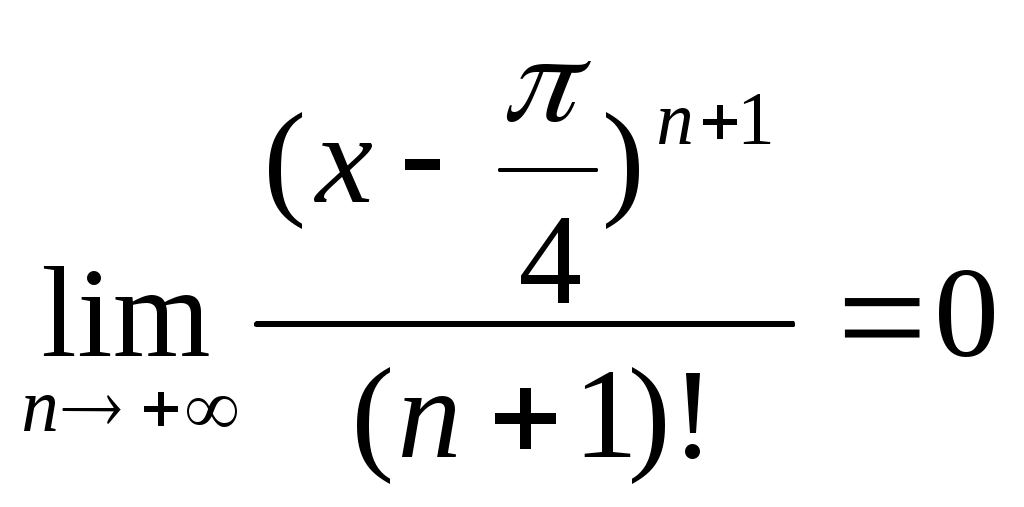, а

Поэтому при любом , т.е. полученный ряд Тейлора для сходится к при любом .

Определение. Если в ряде Тейлора положить x₀=0, получим частный случай ряда Тейлора, который называется рядом Маклорена. Он имеет вид:

---

Остаточный член ряда Маклорена в форме Лагранжа имеет вид:

.

Чтобы он стремился к нулю, достаточно ограниченности производной .

Разложения стандартных функций в ряды Маклорена имеют вид:

1) (сходится при любом x);

2) (сходится при любом x);

3) (сходится при любом x);

4) биномиальный ряд:



(сходится при -1
5) (сходится при -1
6) (сходится при -1≤x≤1).

Пример. Разложить в ряды Маклорена функции:

1) ; 2) ; 3) .

Решение:

1)

Т.к. ряд Маклорена e^x сходится на всей числовой оси, то и полученный ряд сходится к данной функции, при всех значениях x.

2) Преобразуем функцию к виду и воспользуемся биномиальным рядом, в котором положим :



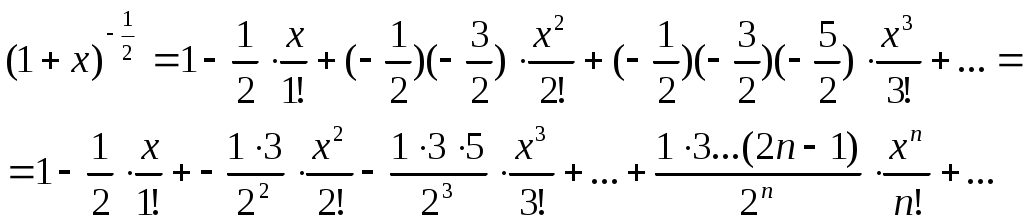
Заменяя в этом выражении x на 3x, получаем:



Окончательно.



Биномиальный ряд сходится при -1 .

3) Преобразуем данную функцию:

. Пишем ряд Маклорена для полученных слагаемых функций

---

(второй ряд получен из первого путем замены x на 2x) и складывая их почленно, имеем:

.
Задачи для решения:
171) Разложить функцию в ряд Тейлора в окрестности точки x=1 (при x₀=1).

172) Разложить функцию в ряд Тейлора в окрестности точки x=1.

173) Разложить функцию в ряд Тейлора в окрестности точки x=-1.

174) Разложить функцию в ряд Тейлора в окрестности точки x=3.

175) Разложить функцию в ряд Тейлора в окрестности точки x=1.

176) Разложить функцию в ряд Тейлора в окрестности точки x=4.

177) Разложить функцию в ряд Тейлора в окрестности точки x=1.

178) Разложить функцию в ряд Тейлора в окрестности точки x=2.

179) Разложить функцию в ряд Тейлора в окрестности точки x=5.
В задачах 180- 186 найти первые пять членов ряда Тейлора для данной функции в окрестности точки x₀:

180)

181)

182)

183)

184)

185)

186)

---

В задачах 187-201 разложит данные функции в окрестности точки x=0, пользуясь формулами разложения в ряд Маклорена функций e^x, sinx, cosx, ln(1+x), (1+x)^mи arctgx:

187)

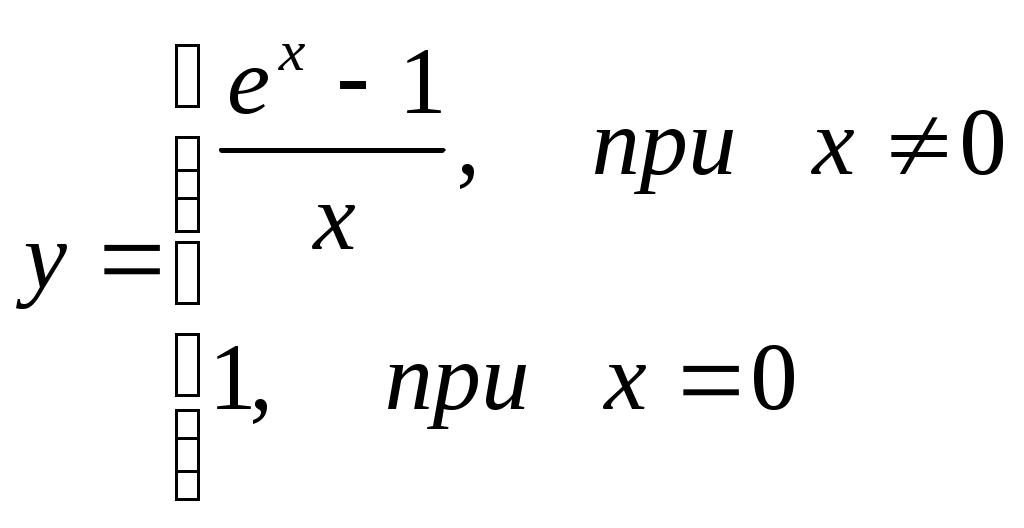
187)

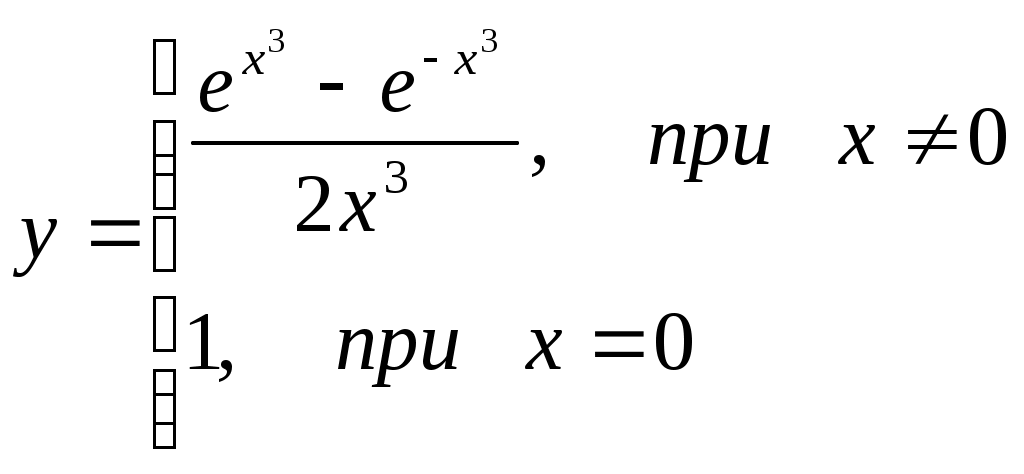
188) .

189)

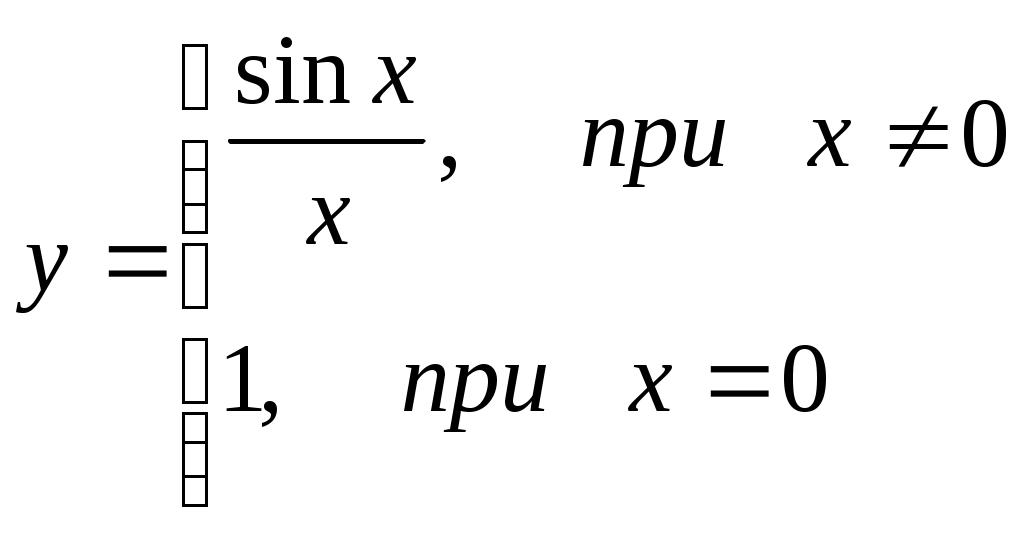
190) .

191)

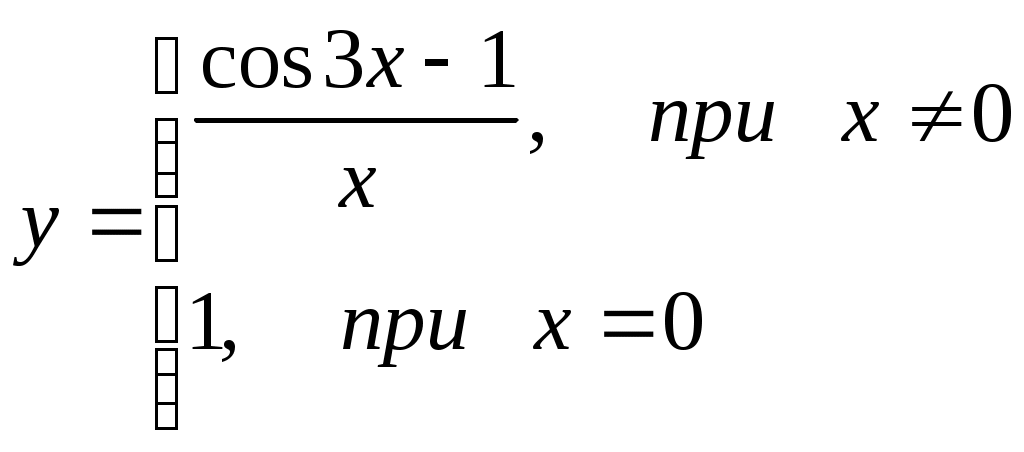
192) .

193) .

194) .

195) .

196) .

197) .

198) .

199) .

200) .

201) .

202) Пользуясь разложением функции в ряд Тейлора, найти значение:

1) седьмой производной функции при x=0,

2) пятой производной функции при x=0,

3) десятой производной функции при x=0.

---

§5. Применение рядов к приближенным вычислениям.
5.1 Приближенное вычисление значений функции.
Допустим, что в окрестности некоторой точке x₀ функция f(x) разлагается в ряд Тейлора. Тогда точное значение функции f(x) в любой точке этой окрестности может быть вычислено по ряду Тейлора, а приближенное ее значение – по частичной сумме этого ряда. Возникающую при этом ошибку можно оценивать по остаточному члену ряда: в случае знакочередующегося ряда – при помощи теоремы Лейбница (ошибка не превосходит по модулю первого отброшенного члени); в случае знакоположительного ряда стараются подобрать другой ряд (обычно геометрическую прогрессию), члены которой больше членов остатка и сумму которой мы можем найти.

Пример. Пользуясь разложением в ряд Маклорена вычислить с точностью до 0,0001 значение .

Решение:

Преобразуем данный корень и применяем биноминальный ряд, пологая , :

.

Чтобы определить, сколько взять первых членов этого знакочередующегося ряда для вычисления с точностью до 0,0001, вычисляем несколько последовательных первых членов ряда: a₁=1; a₂≈0,1562; a₃≈0,00037; a₄≈0,00001.

Согласно теореме Лейбница, если ограничиться суммой первых трех членов ряда, то ошибка искомого приближенного значения будет меньше 2a₄≈2∙0,00001<0,0001.

Следовательно ≈2(1+0,01562-0,00037)≈2,0305.
5.2 Вычисление пределов.
Пример. Вычислить предел, пользуясь разложением функций в ряд Маклорена:



Решение:

Разложим функции в ряды Маклорена:

;

---

Смотрите также файлы

• Теория вероятностей.doc

• Суть стартапа, что это такое.docx

• История Болезни Ф. И. О. больного Чуркин Сергей Геннадьевич 17 лет. Диагноз.doc

• Олимпиада по русскому языку i тур Найди общее начало для частей слов, которые находятся справа, и впиши его.docx

• Основные значения сигналов, подаваемых светофорами (независимо от места установки и их назначения), следующие.pdf