ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 105
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
;  .
.
10.23.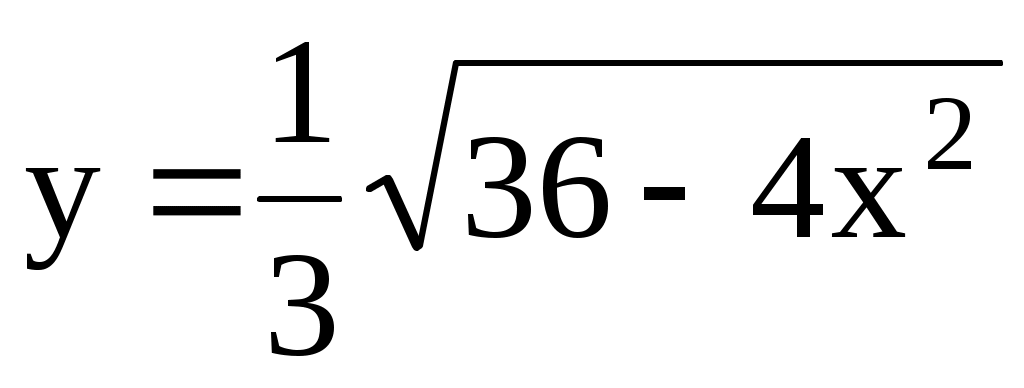 ;
; 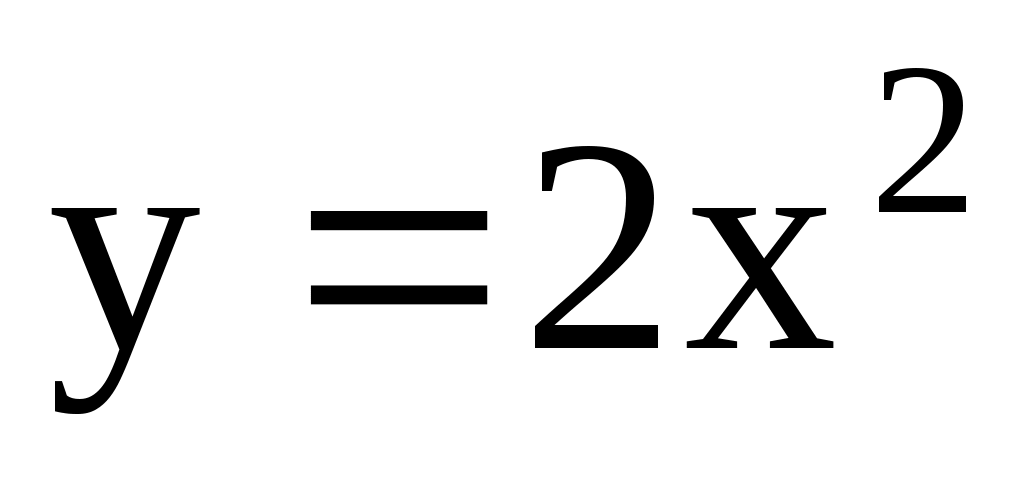 .
.
10.24. ;
; 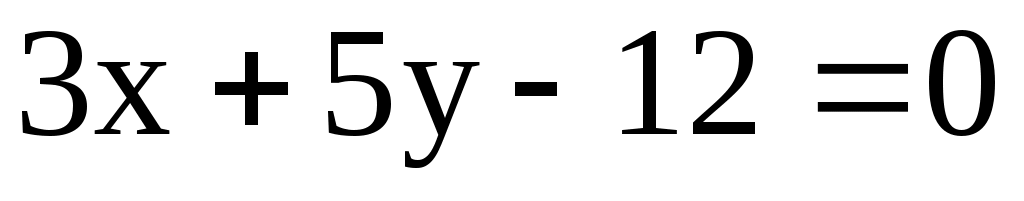 ;
; 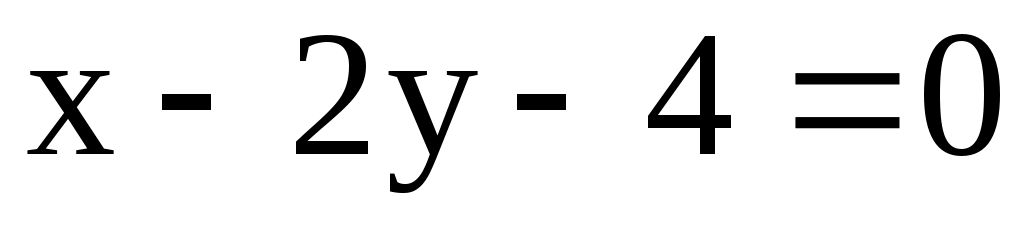 .
.
10.25.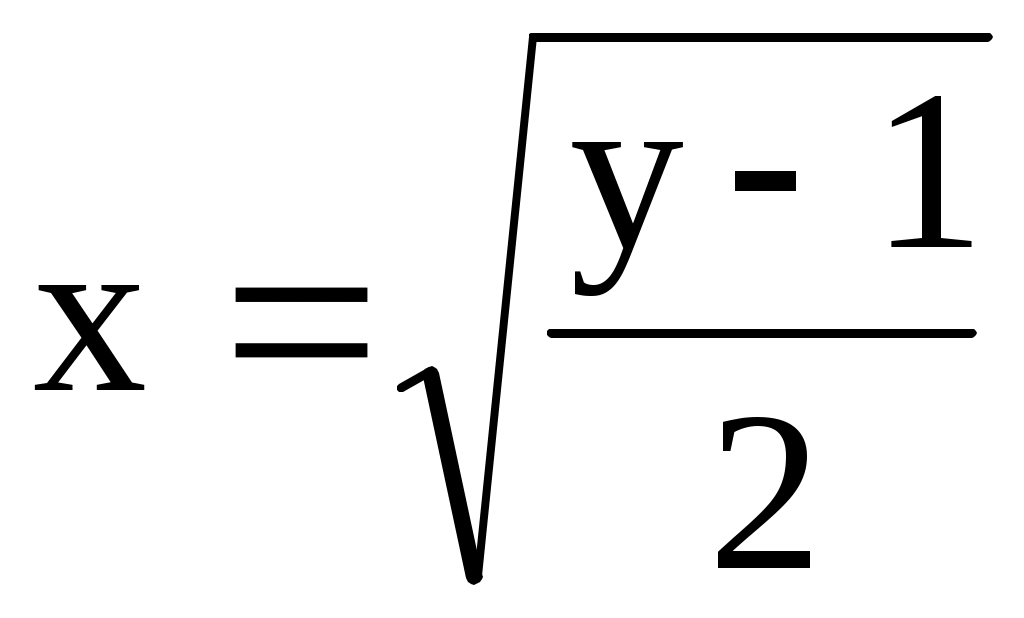 ;
; 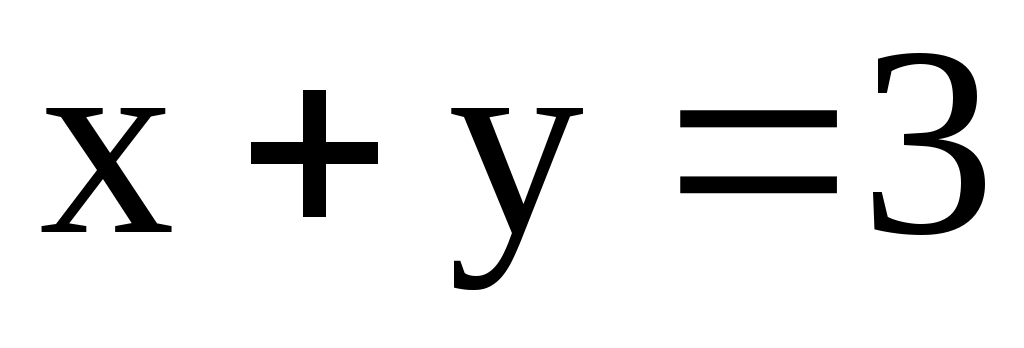 ;
;  ;
;  .
.
10.26.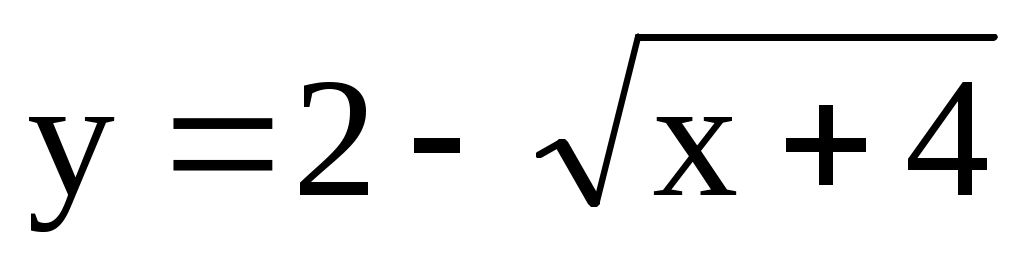 ;
; 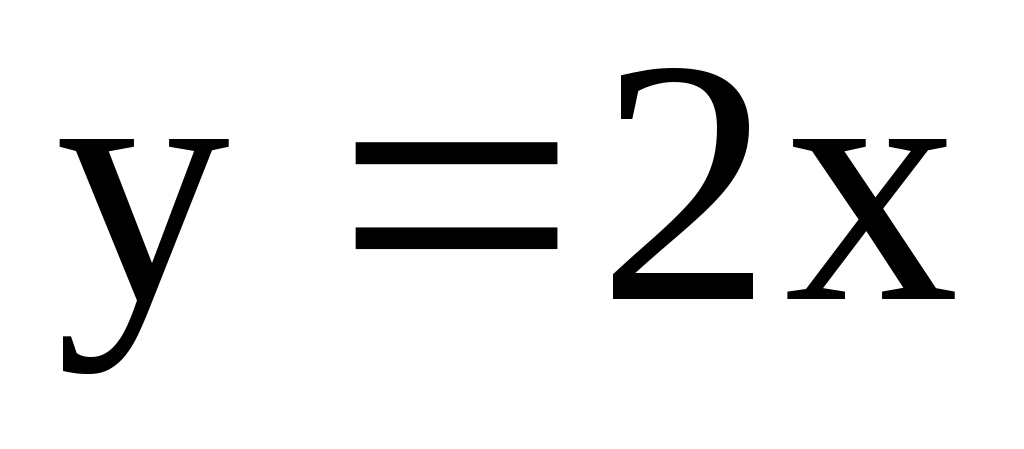 ;
; 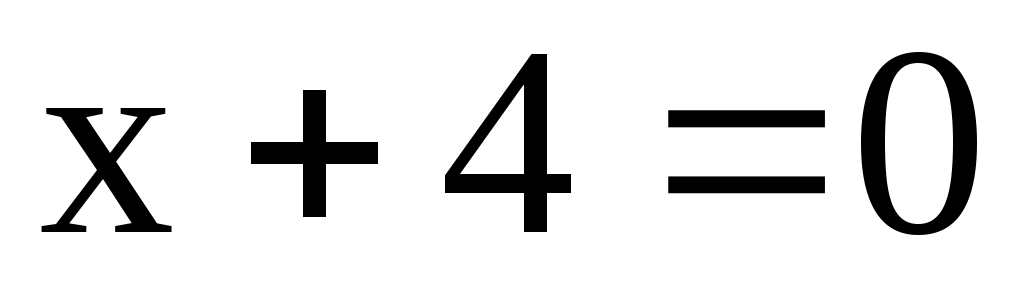 .
.
10.27.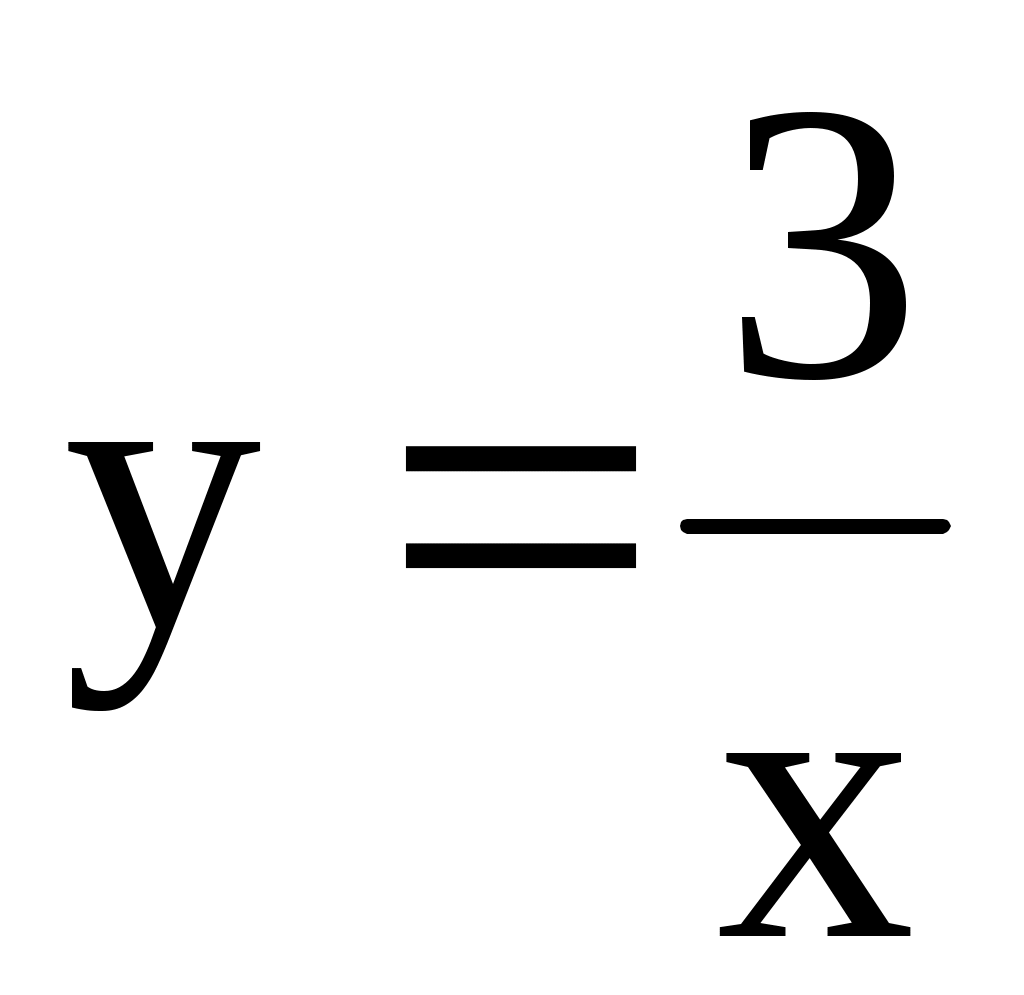 ;
;  ;
; 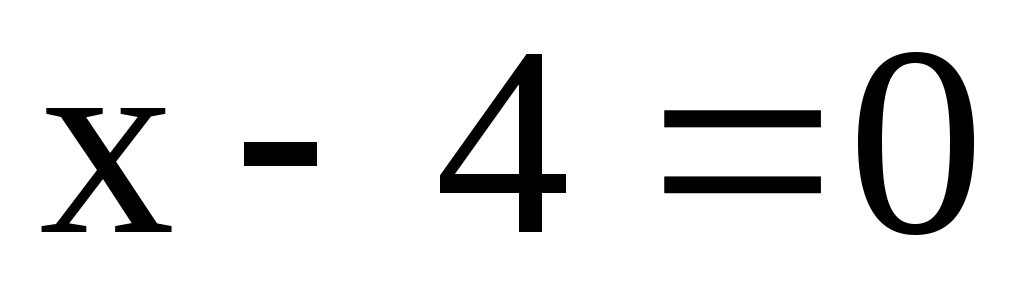 ;
;  .
.
10.28.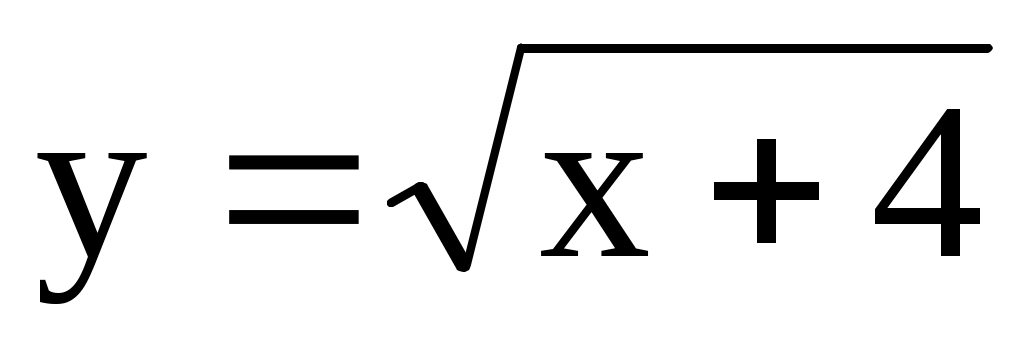 ;
; 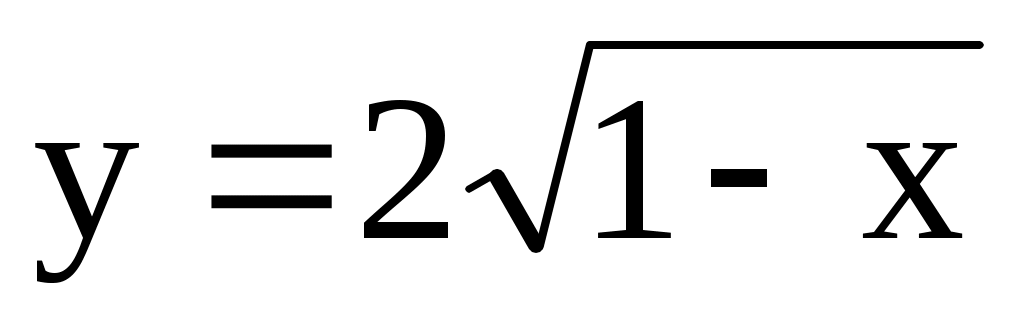 ;
; 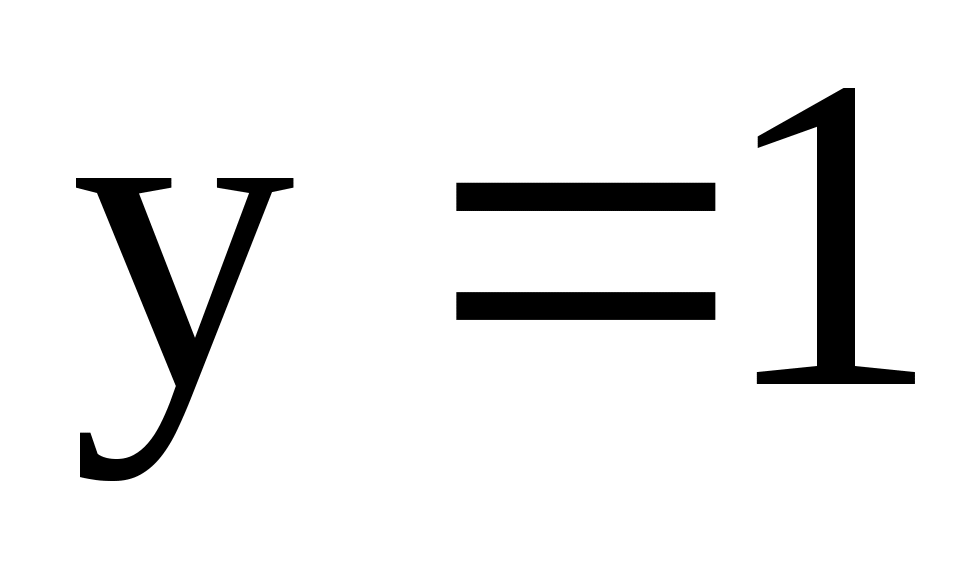 .
.
10.29. ;
; 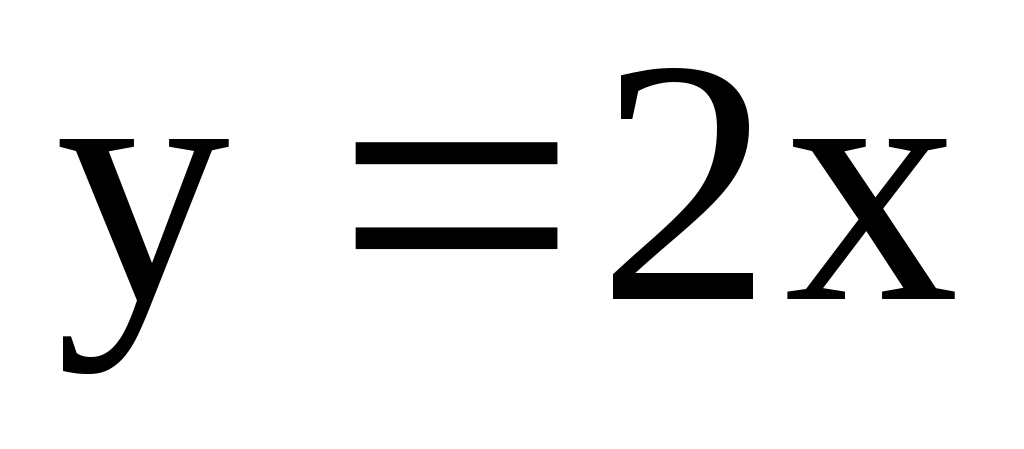 ;
; 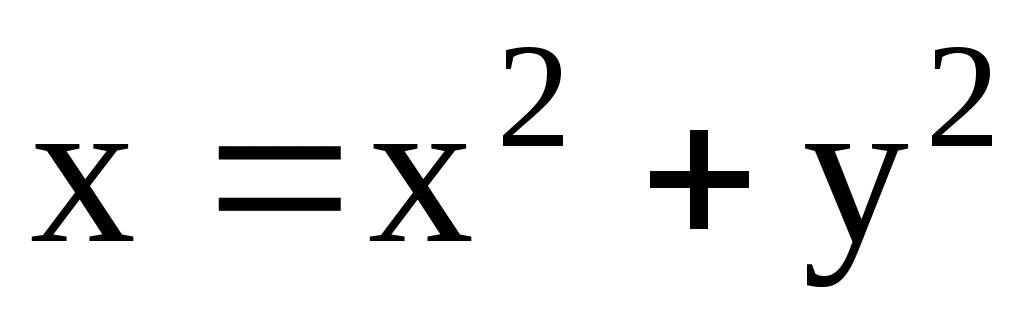 ;
; 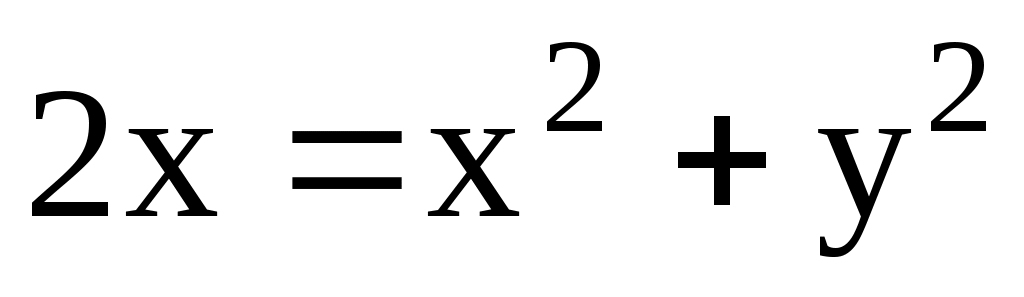 .
.
10.30.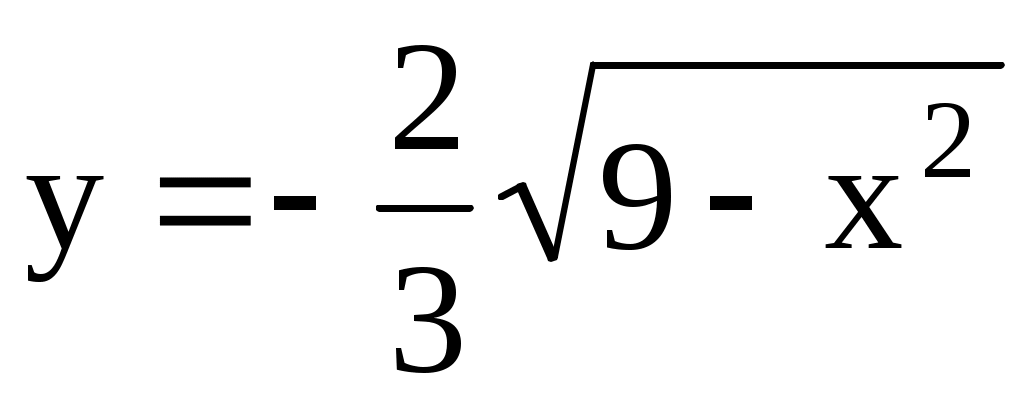 ;
; 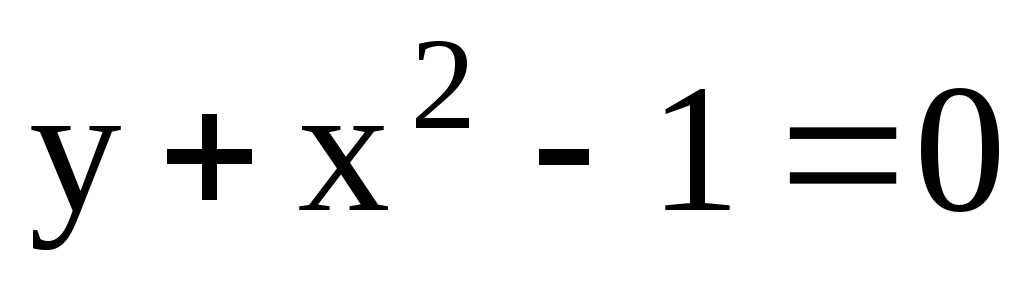 .
.
Задание 11
11.1. Составить уравнение окружности, для которой концами одного диаметра являются точка К(-3; 2) и точка пересечения прямых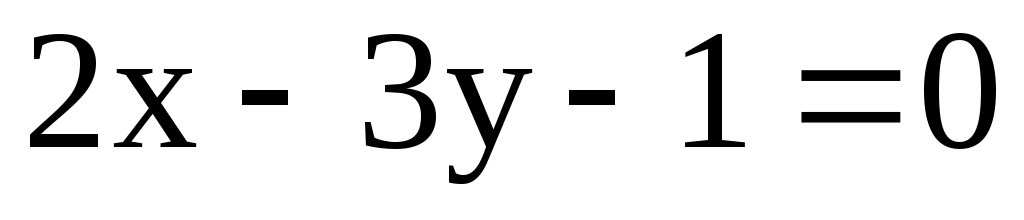 и
и 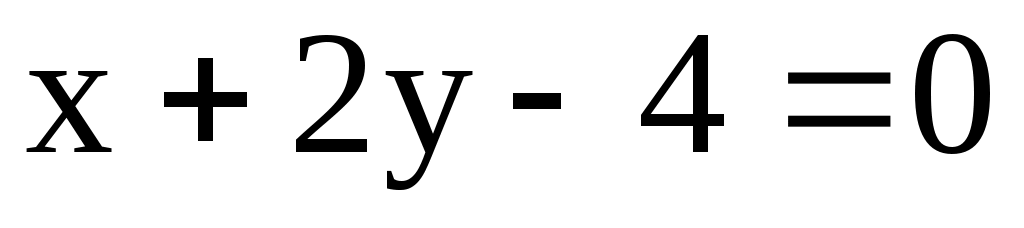 .
.
11.2. Составить уравнение окружности, проходящей через три точки:
А(4; 1), В(-2; 3), С(2; -5).
11.3. Составить уравнение окружности с центром в точке М(1; -3), касающейся прямой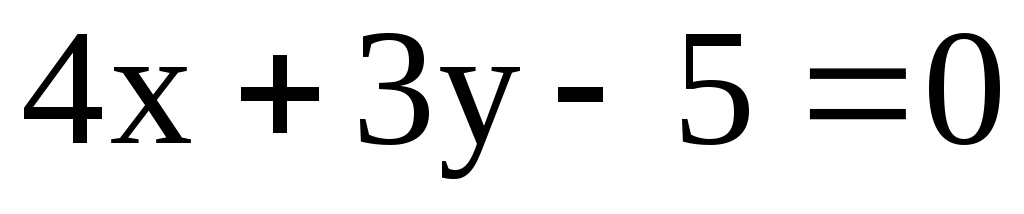 .
.
11.4. Найти кратчайшее расстояние от точки А(-6; 6) до окружности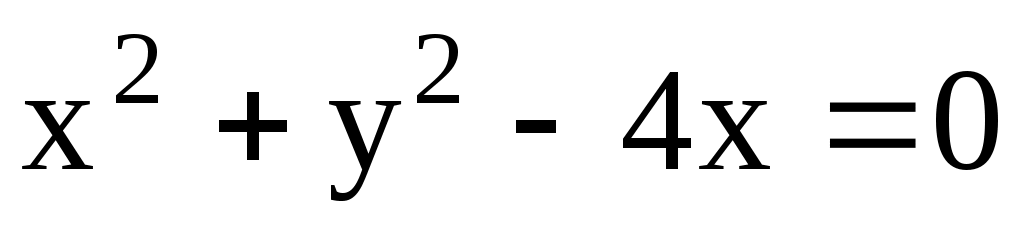 .
.
11.5. Найти расстояние от центра окружности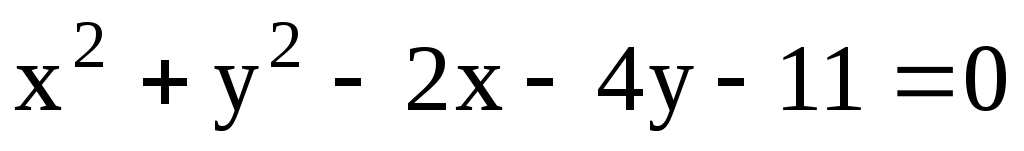 до прямой
до прямой 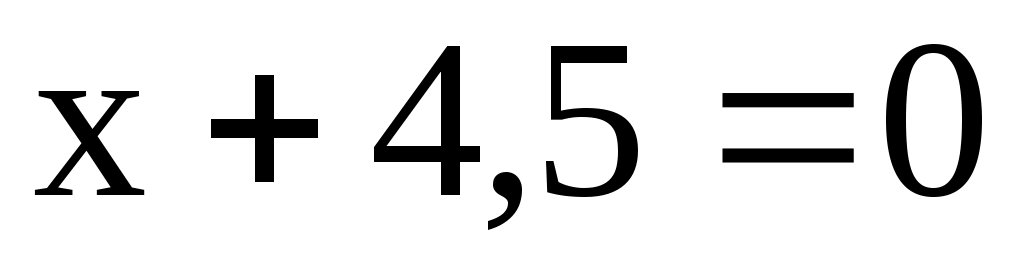 .
.
11.6. Найти расстояние от центра окружности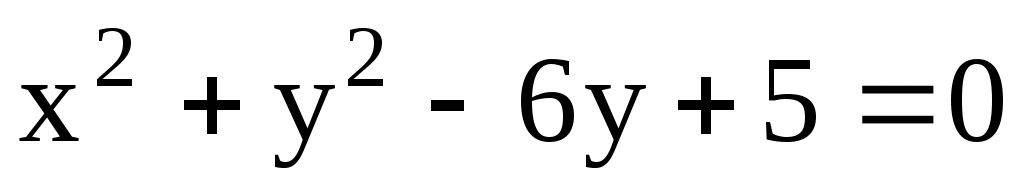 до прямой
до прямой 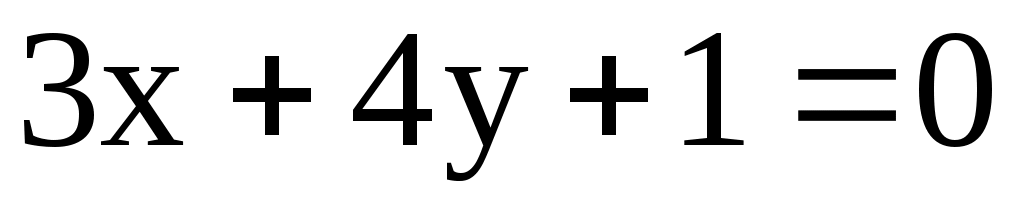 .
.
11.7. Составить уравнение линии центров окружностей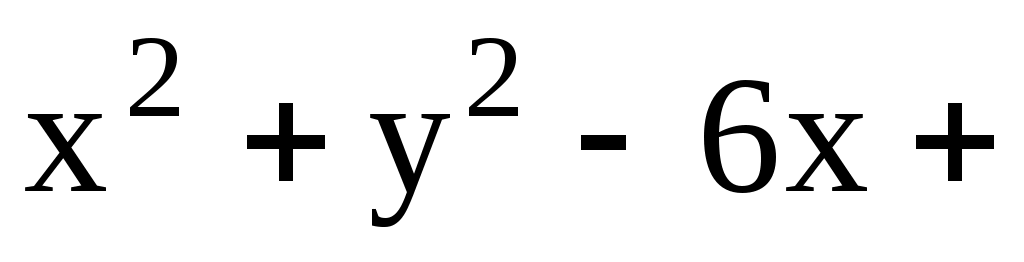
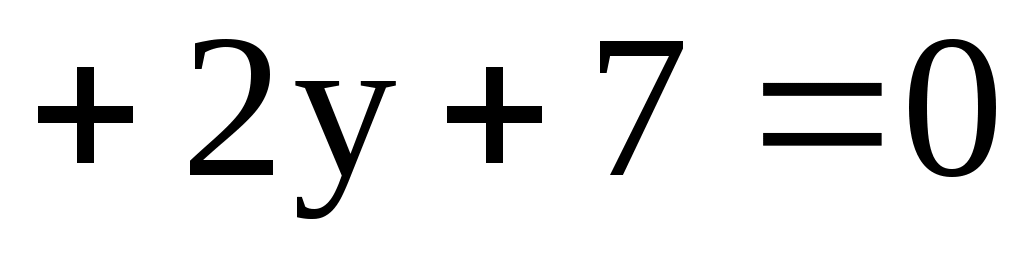 и
и 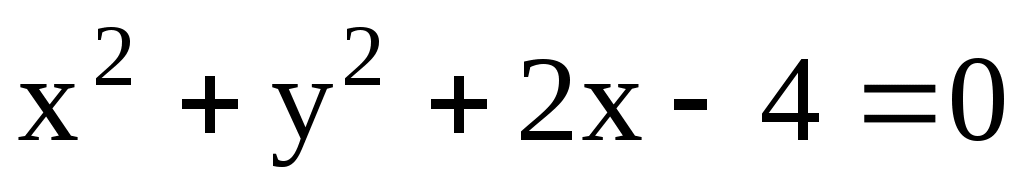 .
.
11.8. Составить уравнение прямой, проходящей через точку С(3; -4) и через центр окружности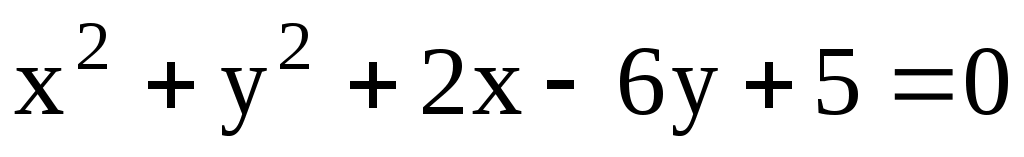 .
.
11.9. Составить уравнение диаметра окружности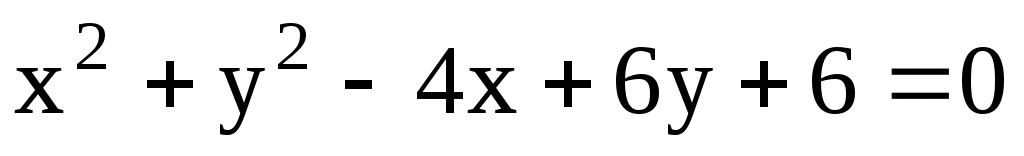 , параллельного прямой
, параллельного прямой 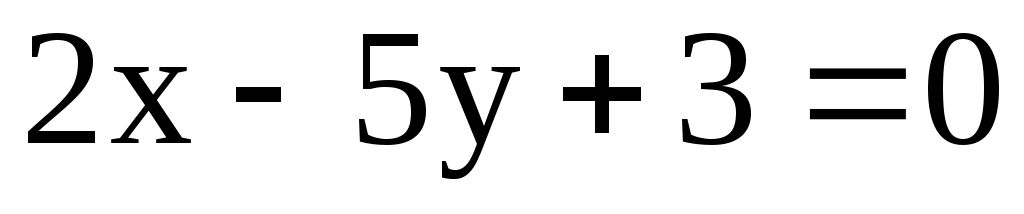 .
.
11.10. Составить уравнение диаметра окружности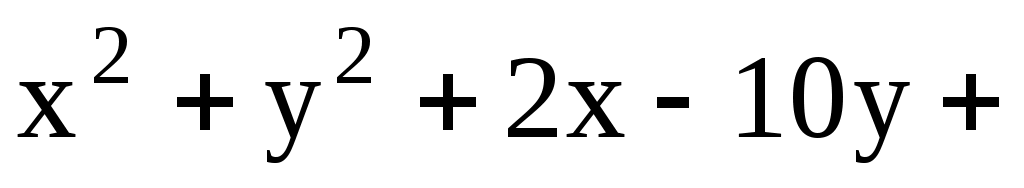
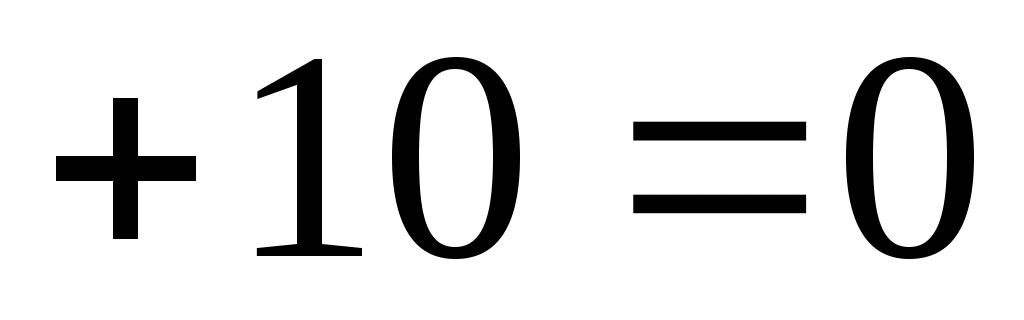 , перпендикулярного прямой
, перпендикулярного прямой 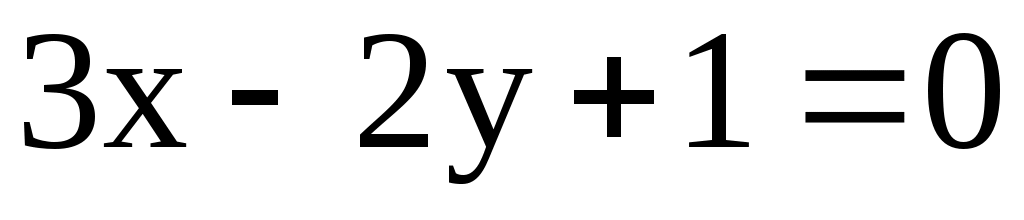 .
.
11.11. Составить уравнение диаметра окружности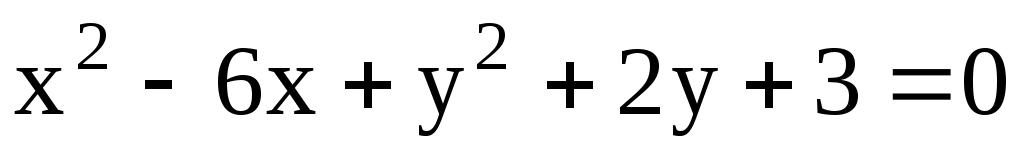
, проходящего через точку пересечения прямых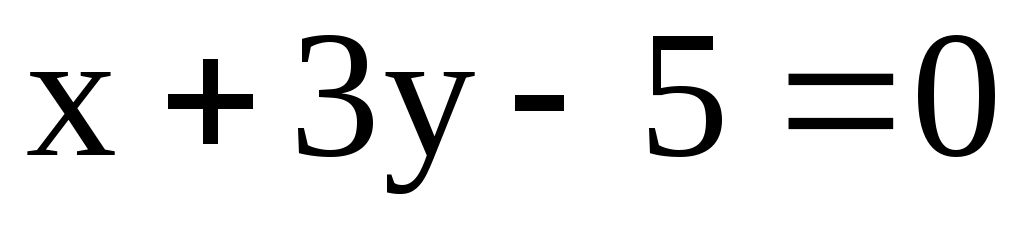 и
и  .
.
11.12. Составить уравнение диаметра окружности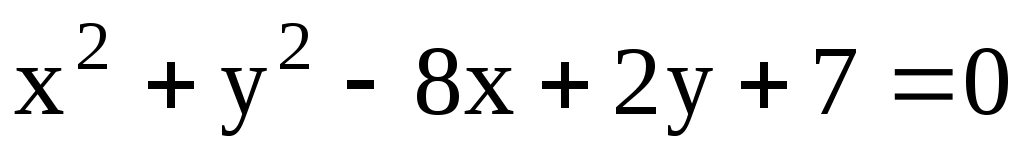 , параллельного биссектрисе II – IV координатных углов.
, параллельного биссектрисе II – IV координатных углов.
11.13. Составить уравнение касательных к окружности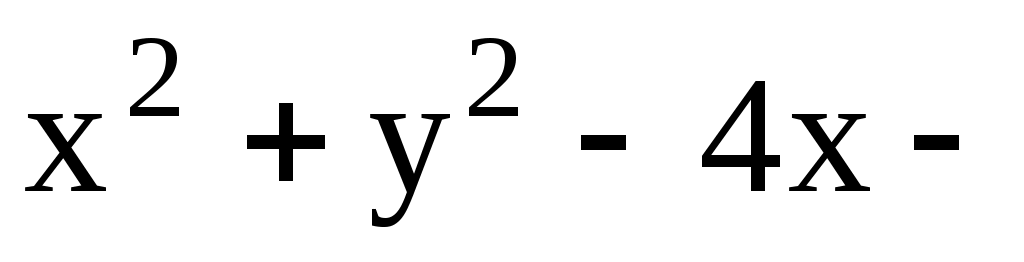
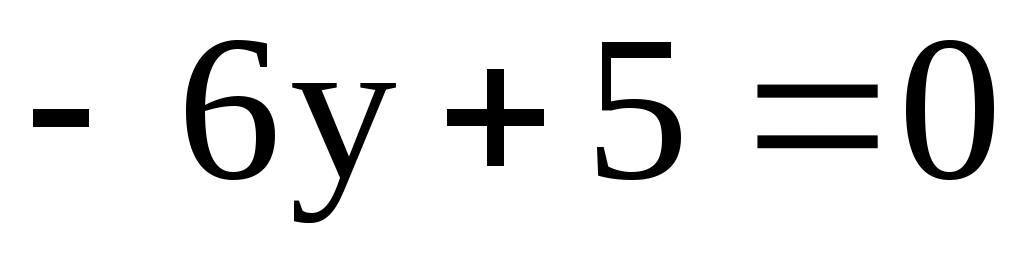 в точках её пересечения с осью Oy.
в точках её пересечения с осью Oy.
11.14. Составить уравнение касательных к окружности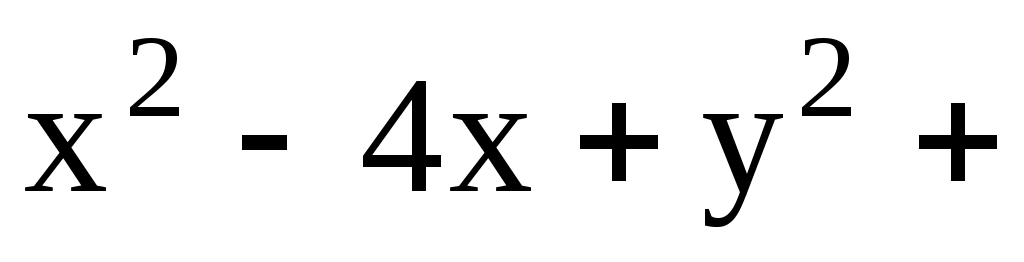
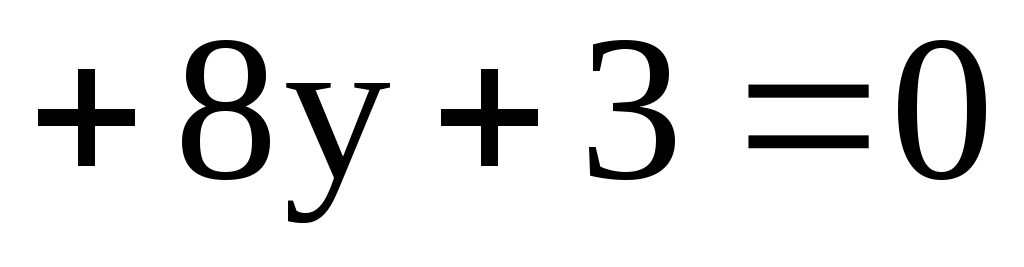 в точках её пересечения с осью Ox.
в точках её пересечения с осью Ox.
11.15. Составить уравнения касательных к окружности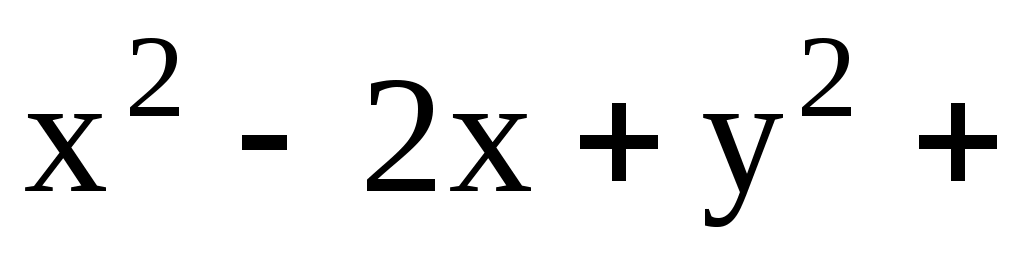
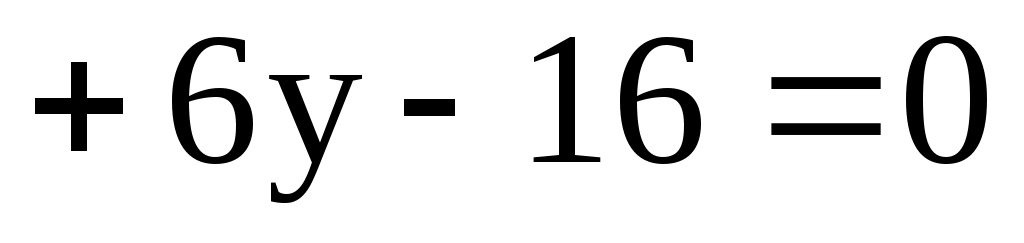 в точках её пересечения с биссектрисой I – III координатных углов.
в точках её пересечения с биссектрисой I – III координатных углов.
11.16. Найти центр и полуоси эллипса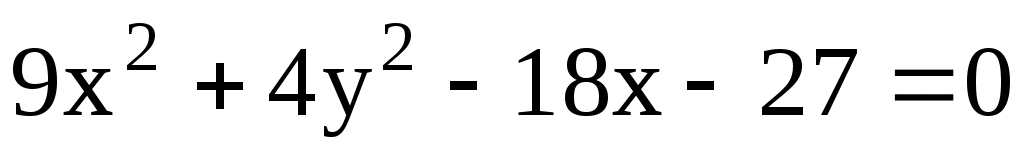 . Сделать чертёж.
. Сделать чертёж.
11.17. Для эллипса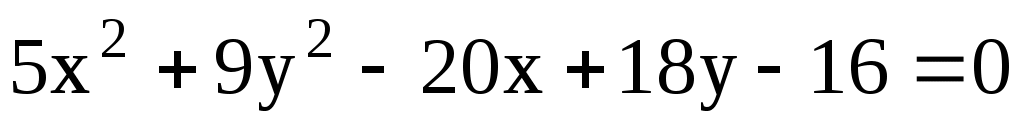 найти его межфокусное расстояние.
найти его межфокусное расстояние.
11.18. Составить уравнение прямой, проходящей через точку С(-3; 4) и через центр эллипса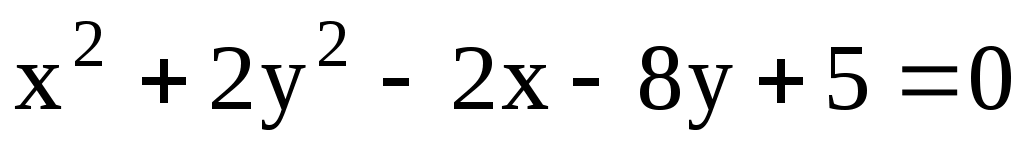 .
.
11.19. Найти эксцентриситет эллипса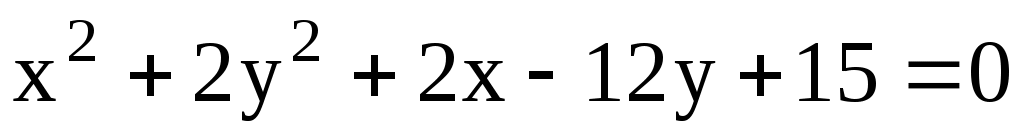 .
.
11.20. Фокусы эллипса совпадают с фокусами гиперболы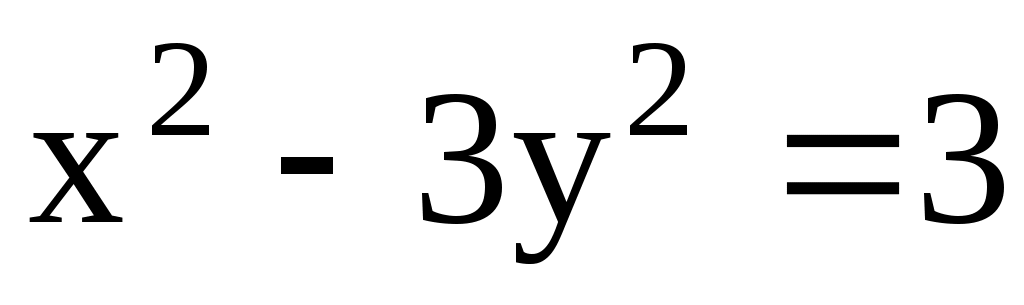 . Составить каноническое уравнение эллипса, если его эксцентриситет
. Составить каноническое уравнение эллипса, если его эксцентриситет 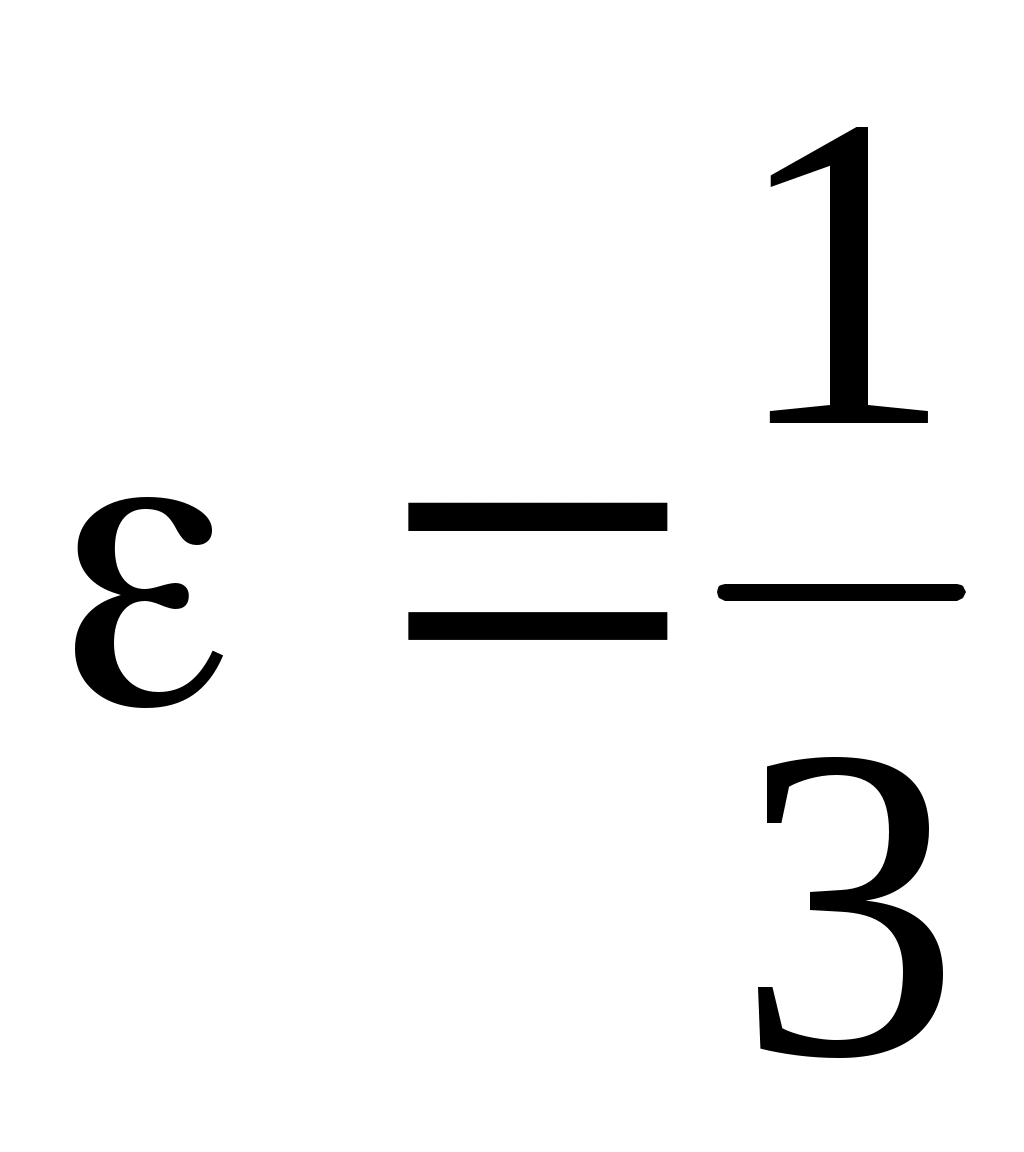 .
.
11.21. Через фокус эллипса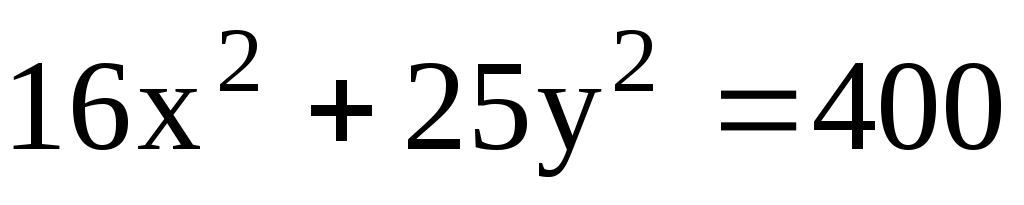 проведена хорда, перпендикулярная к его большой оси. Найти длину хорды.
проведена хорда, перпендикулярная к его большой оси. Найти длину хорды.
11.22. Для гиперболы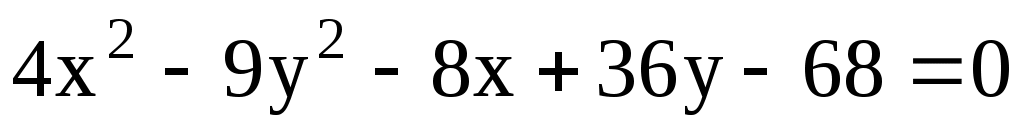 найти полуоси и координаты центра. Сделать чертёж.
найти полуоси и координаты центра. Сделать чертёж.
11.23. Составить уравнение прямой, проходящей через точку М(-1; 3) и через центр гиперболы
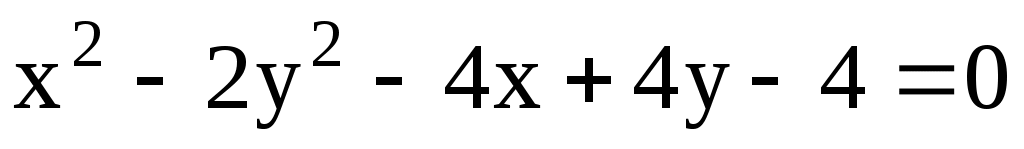 .
.
11.24. Найти координаты фокусов гиперболы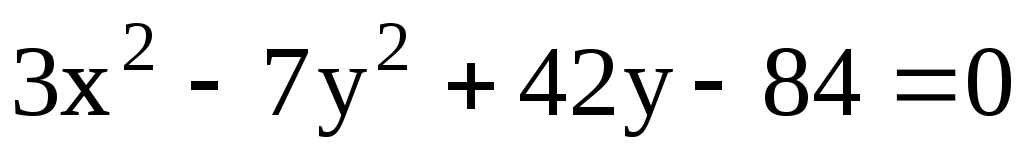 .
.
11.25. Найти эксцентриситет гиперболы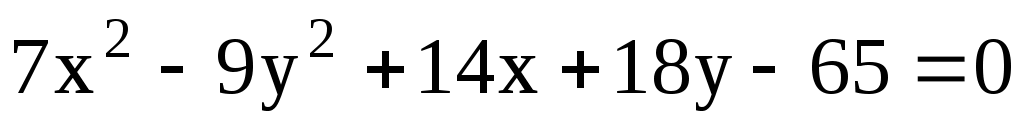 .
.
11.26. Составить уравнения асимптот гиперболы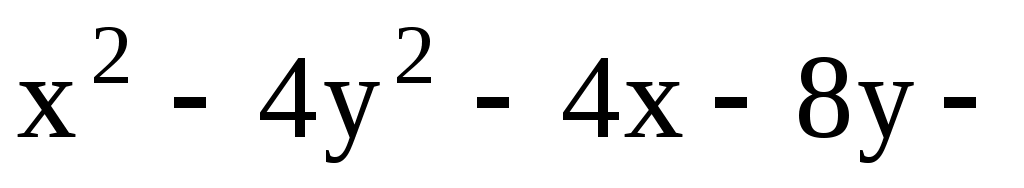
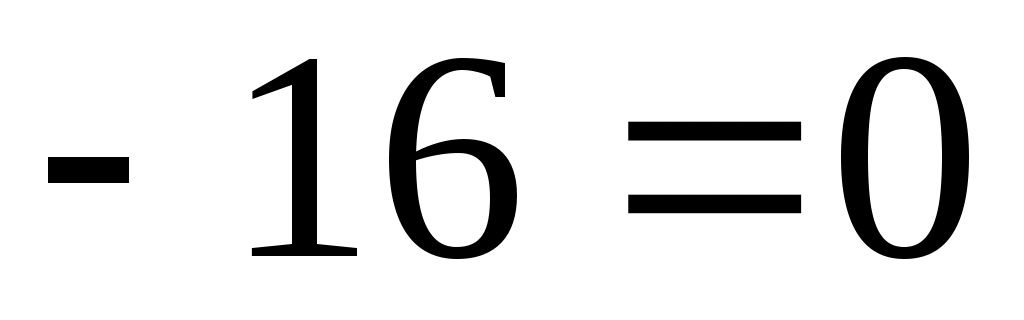 .
.
11.27. Через фокус гиперболы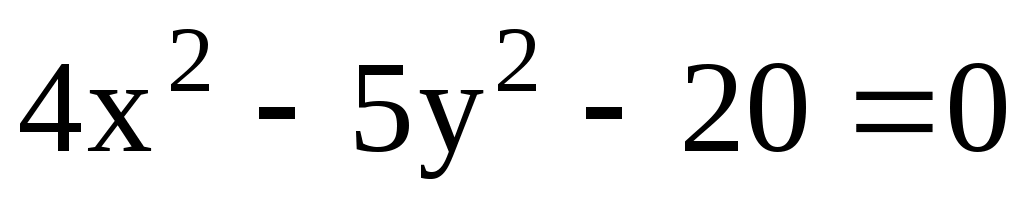 проведена хорда, перпендикулярная к её действительной оси. Найти длину хорды.
проведена хорда, перпендикулярная к её действительной оси. Найти длину хорды.
11.28. Составить уравнение прямой, проходящей через фокус параболы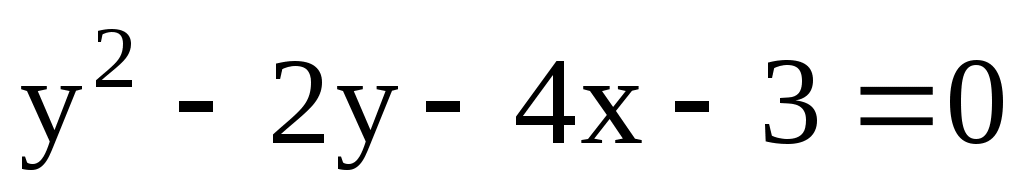 и через точку К(2; 5).
и через точку К(2; 5).
11.29. Составить уравнение прямой, проходящей через вершину параболы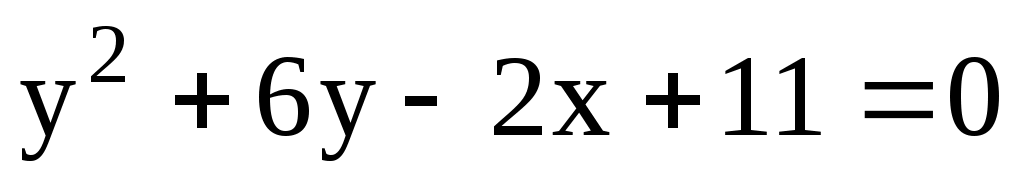 и через точку Р(2; 4).
и через точку Р(2; 4).
11.30. Через фокус параболы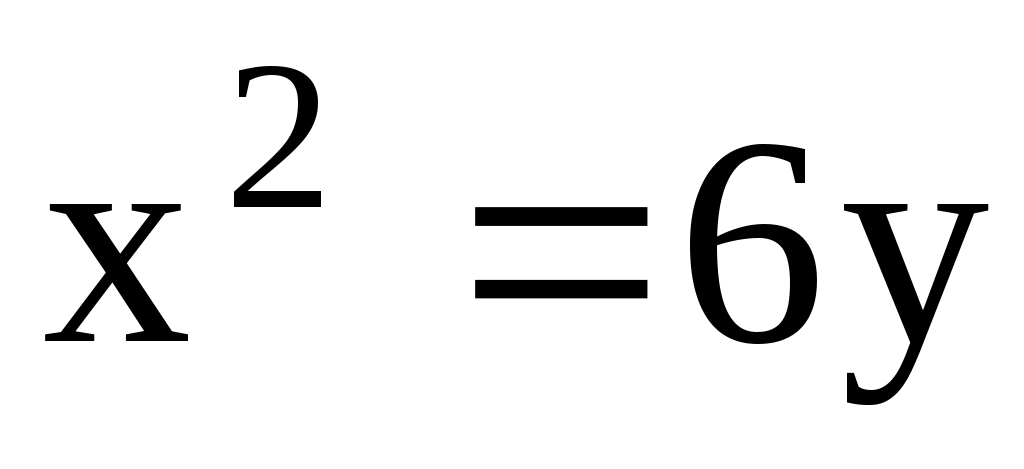 проведена хорда, параллельная оси Ox. Найти её длину.
проведена хорда, параллельная оси Ox. Найти её длину.
Задание 12
Даны координаты вершин пирамиды А1, А2, А3, А4; а) составить уравнение плоскости А1А2А3; б) составить уравнения рёбер А1А2, А1А4 и высоты, опущенной из вершины А4 на грань А1А2А3; в) найти угол между рёбрами А1А2 и А1А4; г) найти угол между ребром А1А4 и гранью А1А2А3.
Задание 13
13.1. Составить уравнение плоскости, проходящей через точку М перпендикулярно плоскостям 1 и 2, если:
а) М(1; -1; 2); 1: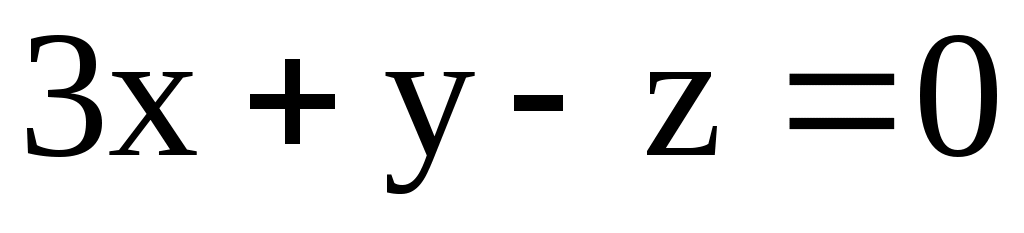 ; 2:
; 2: 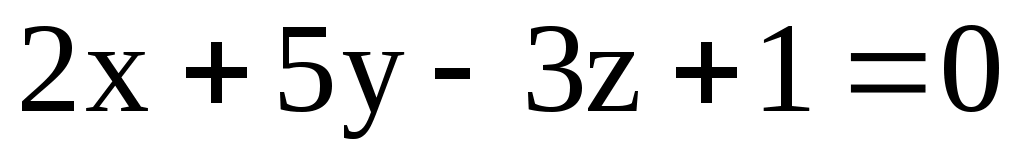 .
.
б) М(2; 1; -3); 1: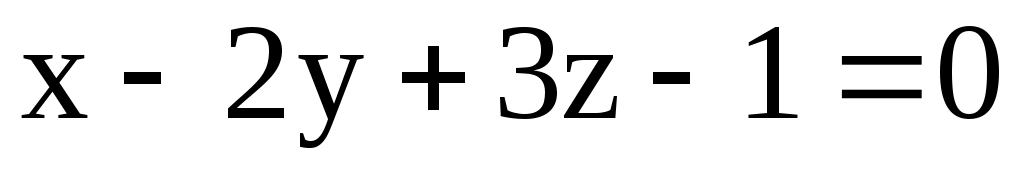 ; 2:
; 2: 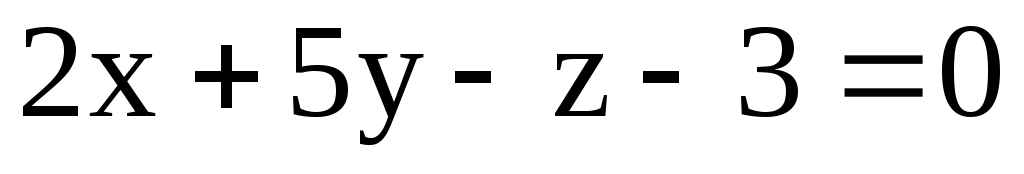 .
.
в) М(-1; 2; 2); 1: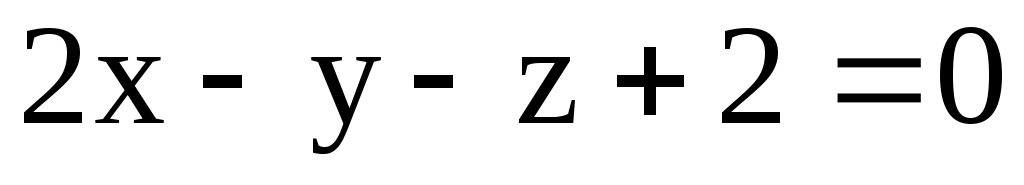 ; 2:
; 2: 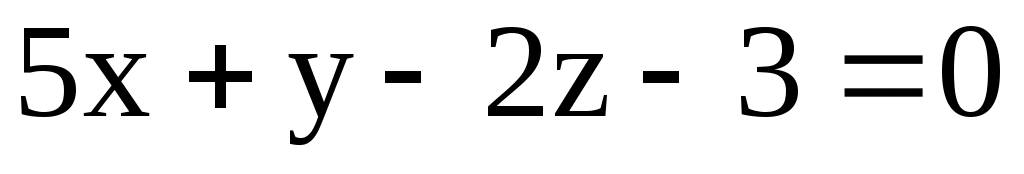 .
.
13.2. Составить уравнение плоскости, проходящей через точки М и N перпендикулярно плоскости , если:
а) М(3; 3; 1); N(-1; 2; 2); :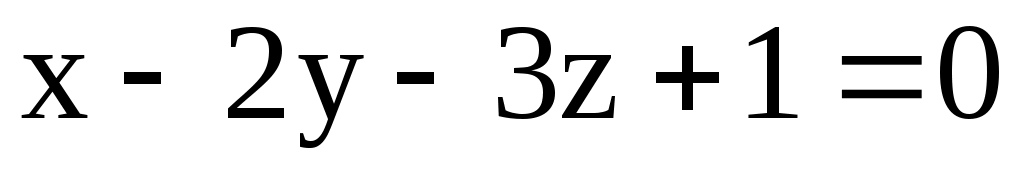 .
.
б) М(-2; 1; 2); N(3; 1; 3); :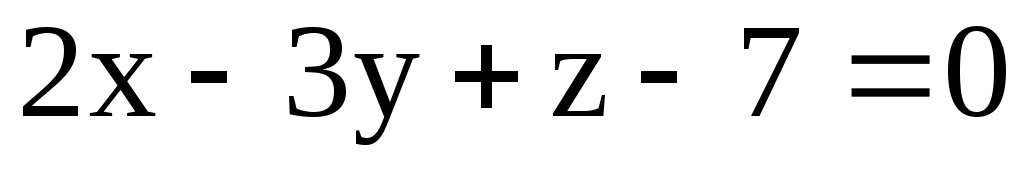 .
.
в) М(1; 2; -1); N(2; 0; 4); :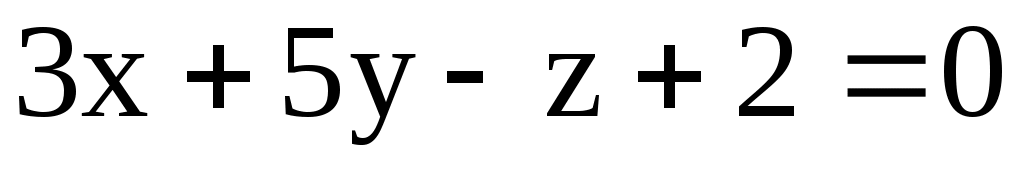 .
.
13.3. Составить уравнение плоскости, проходящей через точку М параллельно прямым l1 и l2, если:
а) М(1; 2; -3); l1: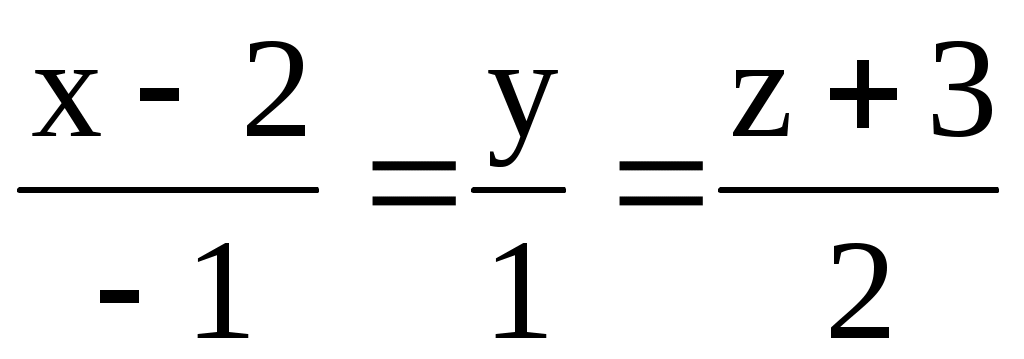 ; l2:
; l2: 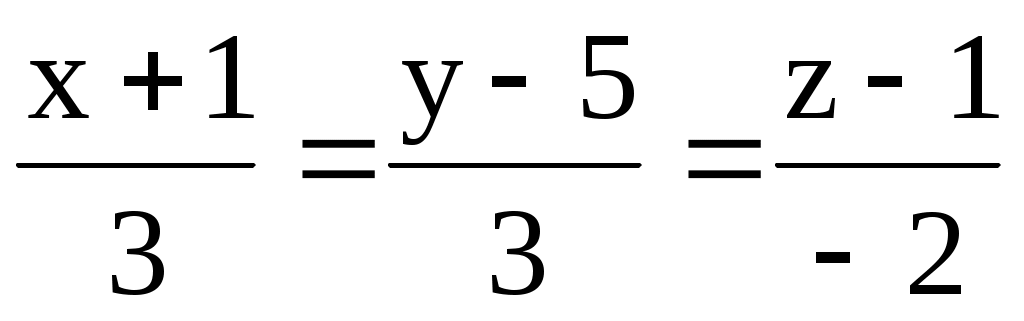 .
.
б) М(-2; 1; 2); l1: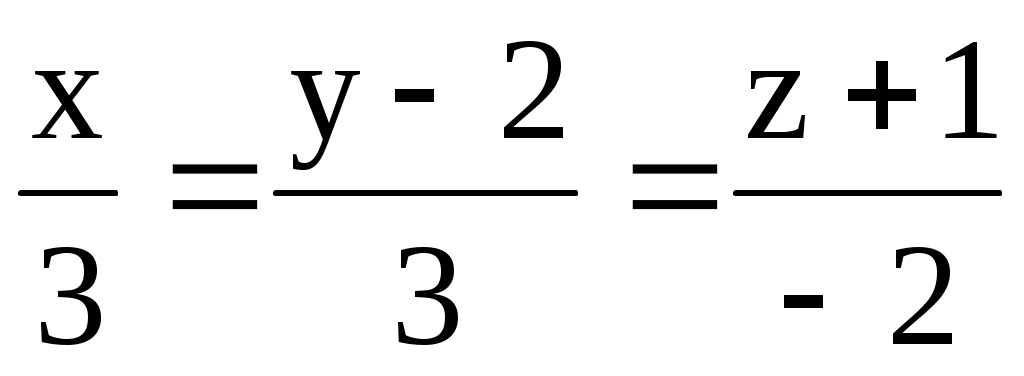 ; l2:
; l2: 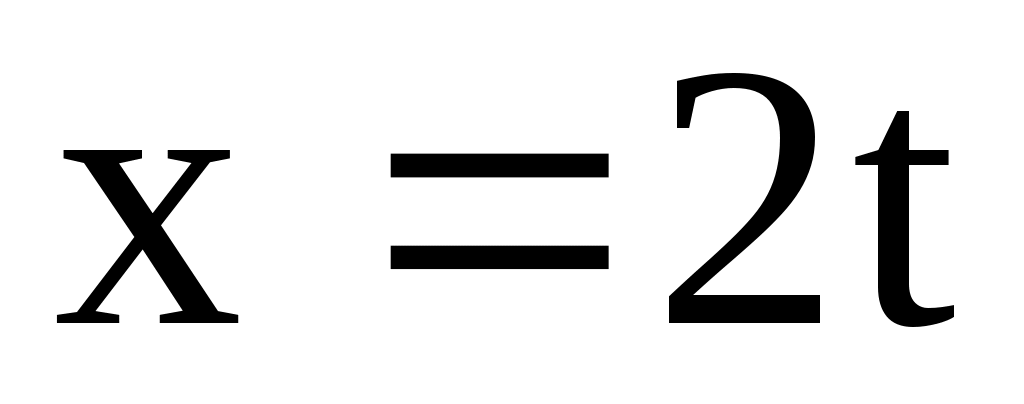 ;
; 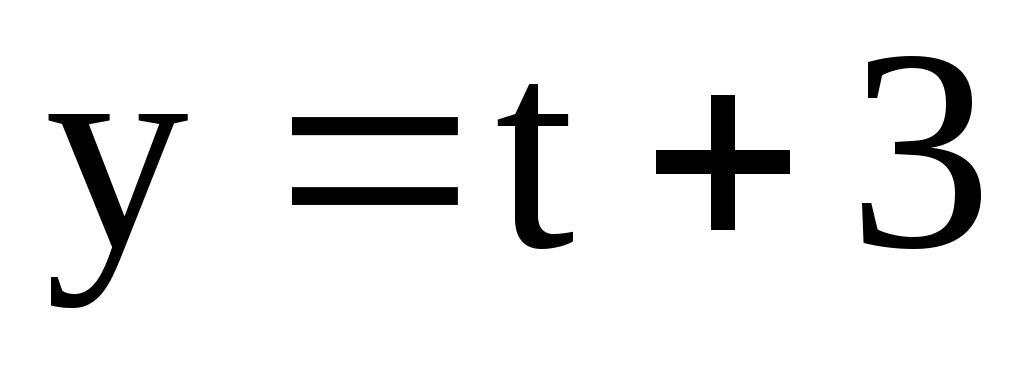 ;
; 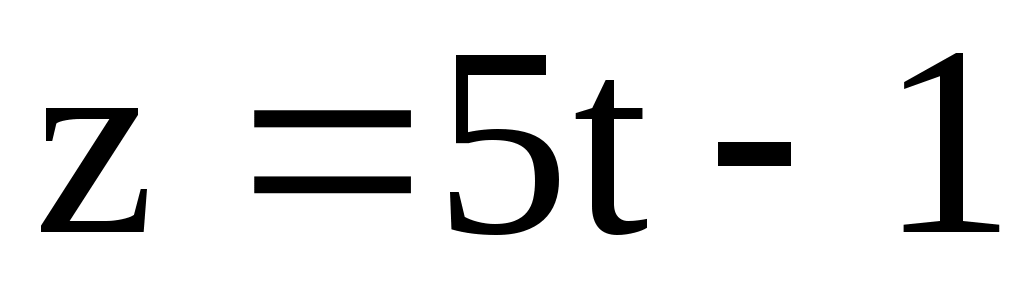 .
.
в) М(3; 0; 1); l1: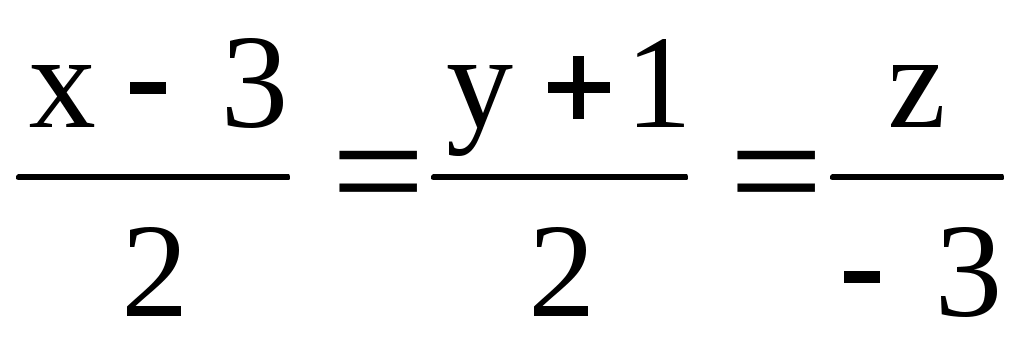 ; l2:
; l2: 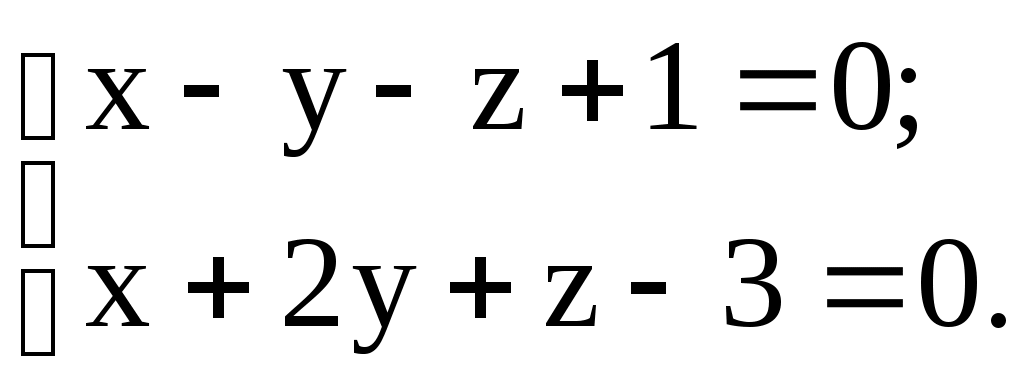
13.4. Составить уравнение плоскости, проходящей через точку М и через прямую l, если:
а) М(1; -1; 1); l: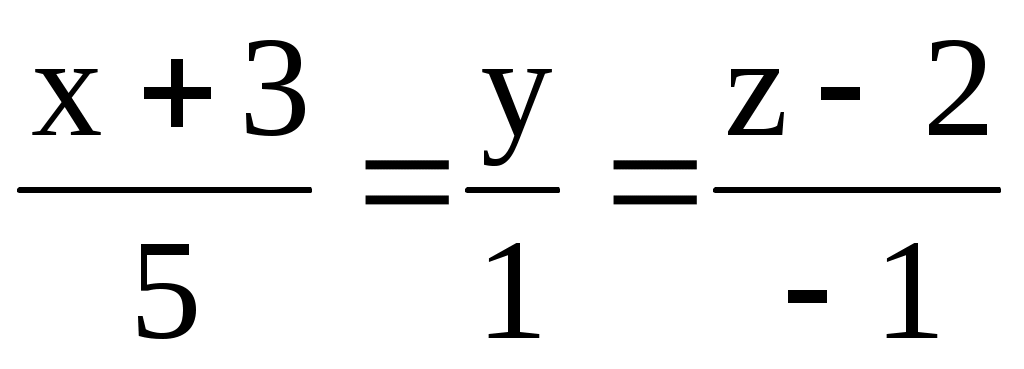 .
.
б) М(3; 1; -2); l: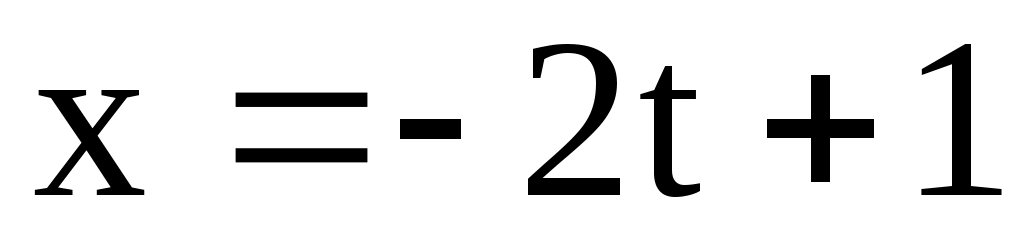
10.23.
10.24.
10.25.
10.26.
10.27.
10.28.
10.29.
10.30.
Задание 11
11.1. Составить уравнение окружности, для которой концами одного диаметра являются точка К(-3; 2) и точка пересечения прямых
11.2. Составить уравнение окружности, проходящей через три точки:
А(4; 1), В(-2; 3), С(2; -5).
11.3. Составить уравнение окружности с центром в точке М(1; -3), касающейся прямой
11.4. Найти кратчайшее расстояние от точки А(-6; 6) до окружности
11.5. Найти расстояние от центра окружности
11.6. Найти расстояние от центра окружности
11.7. Составить уравнение линии центров окружностей
11.8. Составить уравнение прямой, проходящей через точку С(3; -4) и через центр окружности
11.9. Составить уравнение диаметра окружности
11.10. Составить уравнение диаметра окружности
11.11. Составить уравнение диаметра окружности
, проходящего через точку пересечения прямых
11.12. Составить уравнение диаметра окружности
11.13. Составить уравнение касательных к окружности
11.14. Составить уравнение касательных к окружности
11.15. Составить уравнения касательных к окружности
11.16. Найти центр и полуоси эллипса
11.17. Для эллипса
11.18. Составить уравнение прямой, проходящей через точку С(-3; 4) и через центр эллипса
11.19. Найти эксцентриситет эллипса
11.20. Фокусы эллипса совпадают с фокусами гиперболы
11.21. Через фокус эллипса
11.22. Для гиперболы
11.23. Составить уравнение прямой, проходящей через точку М(-1; 3) и через центр гиперболы
11.24. Найти координаты фокусов гиперболы
11.25. Найти эксцентриситет гиперболы
11.26. Составить уравнения асимптот гиперболы
11.27. Через фокус гиперболы
11.28. Составить уравнение прямой, проходящей через фокус параболы
11.29. Составить уравнение прямой, проходящей через вершину параболы
11.30. Через фокус параболы
Задание 12
Даны координаты вершин пирамиды А1, А2, А3, А4; а) составить уравнение плоскости А1А2А3; б) составить уравнения рёбер А1А2, А1А4 и высоты, опущенной из вершины А4 на грань А1А2А3; в) найти угол между рёбрами А1А2 и А1А4; г) найти угол между ребром А1А4 и гранью А1А2А3.
| № | А1 | А2 | А3 | А4 |
| 12.1 | (10; 6; 6) | (-2; 8; 2) | (6; 8; 9) | (7; 10; 3) |
| 12.2 | (1; 8; 2) | (5; 2; 6) | (5; 7; 4) | (4; 10; 9) |
| 12.3 | (6; 6; 5) | (4; 9; 5) | (4; 6; 11) | (6; 9; 3) |
| 12.4 | (7; 2; 2) | (5; 7; 7) | (5; 3; 1) | (2; 3; 7) |
| 12.5 | (6; 6; 4) | (10; 5; 5) | (5; 6; 8) | (8; 10; 7) |
| 12.6 | (7; 7; 2) | (6; 5; 8) | (3; 5; 8) | (8; 4; 10) |
| 12.7 | (-3; 1; 4) | (1; 6; 1) | (1; 1; 6) | (0; 4; -1) |
| 12.8 | (-3; 3; 9) | (-6; 9; 1) | (-1; 7; 3) | (-8; 5; 8) |
| 12.9 | (-3; 5; 4) | (-5; 8; 3) | (-1; 9; 9) | (-6; 4; 8) |
| 12.10 | (-2; 4; 3) | (-7; 6; 3) | (-4; 9; 3) | (-3; 6; 7) |
| 12.11 | (-9; 5; 5) | (7; 3; 1) | (-5; 7; 8) | (-6; 9; 2) |
| 12.12 | (0; 7; 1) | (-4; 1; 5) | (-4; 6; 2) | (-3; 9; 8) |
| 12.13 | (-5; 5; 4) | (-3; 8; 4) | (-3; 5; 10) | (-5; 8; 2) |
| 12.14 | (-6; 1; 1) | (-4; 6; 6) | (-4; 2; 0) | (-1; 2; 6) |
| 12.15 | (-7; 5; 3) | (-9; 4; 4) | (-4; 5; 7) | (-7; 9; 6) |
| 12.16 | (-6; 6; 2) | (-5; 4; 7) | (-2; 4; 7) | (-7; 3; 0) |
| 12.17 | (3; 1; 4) | (-1; 6; 1) | (-1; 1; 6) | (0; 4; -1) |
| 12.18 | (3; 3; 9) | (6; 9; 1) | (1; 7; 3) | (8; 5; 8) |
| 12.19 | (3; 5; 4) | (5; 8; 3) | (1; 9; 9) | (6; 4; 8) |
| 12.20 | (2; 4; 3) | (7; 6; 3) | (4; 9; 3) | (3; 6; 9) |
| 12.21 | (9; 5; 5) | (-3; 7; 1) | (5; 7; 8) | (6; 9; 2) |
| 12.22 | (0; 7; 1) | (4; 1; 5) | (4; 6; 3) | (3; 9; 8) |
| 12.23 | (5; 5; 4) | (3; 8; 4) | (3; 5; 10) | (5; 8; 2) |
| 12.24 | (6; 1; 1) | (4; 6; 6) | (4; 2; 0) | (1; 2; 6) |
| 12.25 | (7; 5; 3) | (9; 4; 4) | (4; 5; 7) | (7; 9; 6) |
| 12.26 | (6; 6; 2) | (5; 4; 7) | (2; 4; 7) | (7; 3; 0) |
| 12.27 | (4; 2; 5) | (0; 7; 2) | (0; 2; 7) | (1; 5; 0) |
| 12.28 | (4; 4; 10) | (7; 10; 2) | (2; 8; 4) | (9; 6; 9) |
| 12.29 | (4; 6; 5) | (6; 9; 4) | (2; 10; 10) | (7; 5; 9) |
| 12.30 | (3; 5; 4) | (8; 7; 4) | (5; 10; 4) | (4; 7; 8) |
Задание 13
13.1. Составить уравнение плоскости, проходящей через точку М перпендикулярно плоскостям 1 и 2, если:
а) М(1; -1; 2); 1:
б) М(2; 1; -3); 1:
в) М(-1; 2; 2); 1:
13.2. Составить уравнение плоскости, проходящей через точки М и N перпендикулярно плоскости , если:
а) М(3; 3; 1); N(-1; 2; 2); :
б) М(-2; 1; 2); N(3; 1; 3); :
в) М(1; 2; -1); N(2; 0; 4); :
13.3. Составить уравнение плоскости, проходящей через точку М параллельно прямым l1 и l2, если:
а) М(1; 2; -3); l1:
б) М(-2; 1; 2); l1:
в) М(3; 0; 1); l1:
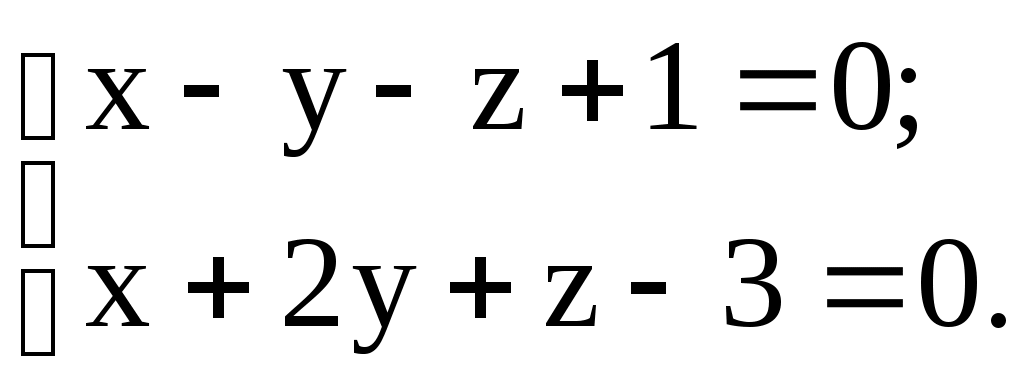
13.4. Составить уравнение плоскости, проходящей через точку М и через прямую l, если:
а) М(1; -1; 1); l:
б) М(3; 1; -2); l: