Файл: Лекция матрицы план Понятие матрицы. Типы матриц. Алгебра матриц.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.12.2023
Просмотров: 109
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Матрицы А и В называются согласованными, если число столбцов матрицы А равно числу строк матрицы В. Так, если  ,
, 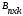 , m≠k, то матрицы А и В согласованные, так как n = n, а в обратном порядке матрицы В и А несогласованные, так как m ≠ k. Квадратные матрицы согласованы, когда у них одинаковый порядок n, причем согласованы как А и В, так и В и А. Если
, m≠k, то матрицы А и В согласованные, так как n = n, а в обратном порядке матрицы В и А несогласованные, так как m ≠ k. Квадратные матрицы согласованы, когда у них одинаковый порядок n, причем согласованы как А и В, так и В и А. Если  , а
, а 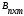 , то будут согласованы матрицы А и В, а также матрицы В и А, так как n = n, m = m.
, то будут согласованы матрицы А и В, а также матрицы В и А, так как n = n, m = m.
Произведением двух согласованных матриц  и
и 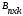
А=
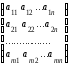 , В=
, В=
называется матрица С порядка mk:
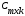 =
= ∙
∙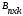 , элементы которой вычисляются по формуле:
, элементы которой вычисляются по формуле: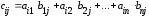 (
( 1, 2, 3, …, m , j=1, 2, 3, …, k),
1, 2, 3, …, m , j=1, 2, 3, …, k),то есть элемент
 i –ой строки и j –го столбца матрицы С равен сумме произведений всех элементов i –ой строки матрицы А на соответствующие элементы j –го столбца матрицы В.
i –ой строки и j –го столбца матрицы С равен сумме произведений всех элементов i –ой строки матрицы А на соответствующие элементы j –го столбца матрицы В.Пример. Найти произведение матриц А и В.
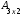 =
=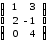 ,
, 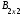 =
=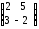 ,
,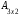 ∙
∙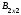 =
=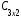 =
=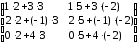 =
=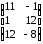 .
.Произведение матриц В∙А не существует, так как матрицы В и А не согласованы: матрица В имеет порядок 22, а матрица А – порядок 32.
Рассмотрим свойства произведения матриц:
1) некоммутативность: АВ ≠ ВА, даже если А и В, и В и А согласованы. Если же АВ = ВА, то матрицы А и В называются коммутирующими (матрицы А и В в этом случае обязательно будут квадратными).
Пример 1.
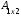 =
= 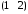 ,
, 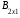 =
=  ;
; 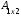
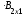 =
=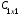 =
=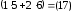 ;
; 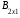
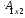 =
=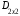 =
=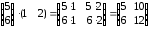 .
. Очевидно, что
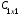 ≠
≠ 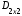 .
.Пример 2.
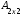 =
= 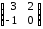 ,
,  =
= 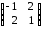 ;
;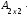
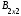 =
= 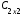 =
= 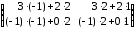 =
=
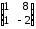 ;
;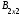
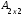 =
= 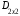 =
= 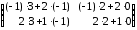 =
= 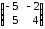 .
.Вывод:
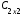 ≠
≠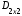 , хотя матрицы
, хотя матрицы 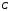 и
и 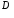 одного порядка.
одного порядка.2) для любых квадратных матриц единичная матрица Е является коммутирующей к любой матрице А того же порядка, причем в результате получим ту же матрицу А, то есть АЕ = ЕА = А.
Пример.
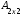 =
=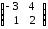
,
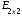 =
=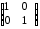 ;
;
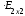 =
=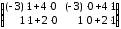 =
=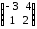 =
= ;
;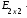
 =
=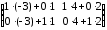 =
=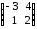 =
= .
.3) A·0 = 0·A = 0.
4) произведение двух матриц может равняться нулю, при этом матрицы А и В могут быть ненулевыми.
Пример.
 =
= 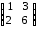 ,
,  =
= 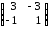 ;
;
 =
= 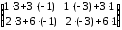 =
=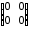 =
=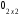 .
.5) ассоциативность АВС=А(ВС)=(АВ)С:
 · (
· ( ·
·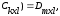
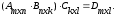
Пример.
Имеем матрицы
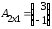 ,
, 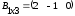 ,
, 
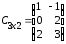 ;
;тогда Аּ(ВּС) =
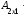 (
(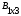 ·
·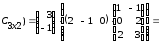
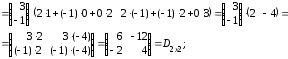
(АּВ)ּС=
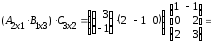
=
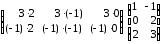 =
=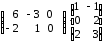 =
==
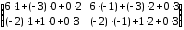 =
=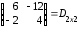 .
.Таким образом, мы на примере показали, что Аּ(ВּС) = (АּВ)ּС.
6) дистрибутивность относительно сложения:
(А+В)∙С = АС + ВС, А∙(В + С)=АВ + АС.
7) (А∙В)
 = В
= В ∙А
∙А .
.Пример.
 =
=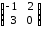 ,
, 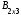 =
=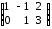 ,
,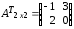 ,
, 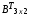 =
=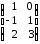 .
.Тогда АВ=
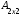 ∙
∙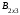 =
=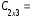
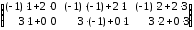 =
==
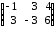
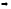 (А∙В)
(А∙В) =
= 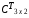 =
=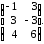
В
 ∙А
∙А =
=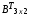 ∙
∙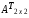 =
= 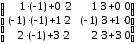 =
=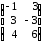 =
=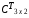 .
.Таким образом, (А∙В)
 = В
= В А
А .
.8) λ(АּВ) = (λА)ּ
В = Аּ (λВ), λ,
 R.
R.Рассмотрим типовые примеры на выполнение действий над матрицами, то есть требуется найти сумму, разность, произведение (если они существуют) двух матриц А и В.
Пример 1.
 ,
, 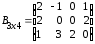 .
.Решение.
1)
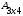 +
+ 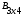 =
= 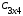 =
= 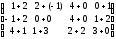 =
=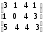 ;
;2)
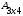 –
– 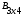 =
=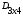 =
=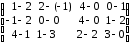 =
=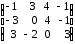 ;
;3) произведение
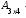
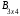 не существует, так как матрицы А и В несогласованы, впрочем, не существует и произведения
не существует, так как матрицы А и В несогласованы, впрочем, не существует и произведения 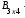
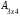 по той же причине.
по той же причине.Пример 2.
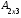 =
=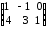 ,
, 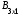 =
= .
.Решение.
1) суммы матриц, как и их разности, не существует, так как исходные матрицы разного порядка: матрица А имеет порядок 23, а матрица В – порядок 31;
2) так как матрицы А и В согласованны, то произведение матриц АּВ существует:
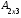 ·
·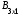 =
=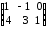 ·
· =
=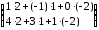 =
=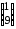 ,
,произведение матриц ВּА не существует, так как матрицы