Файл: Лекция матрицы план Понятие матрицы. Типы матриц. Алгебра матриц.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.12.2023
Просмотров: 107
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
ЛЕКЦИЯ 3. ОБРАТНАЯ МАТРИЦА
План
Свойства обратной матрицы.
ЕДИНСТВЕННОСТЬ ОБРАТНОЙ МАТРИЦЫ
В теории чисел наряду с числом определяют число, противоположное ему (
определяют число, противоположное ему (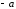 ) такое, что
) такое, что 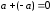 , и число, обратное ему
, и число, обратное ему 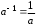 такое, что
такое, что 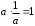 . Например, для числа 5 противоположным будет число
. Например, для числа 5 противоположным будет число
(– 5), а обратным будет число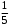 . Аналогично, в теории матриц мы уже ввели понятие противоположной матрицы, ее обозначение (– А). Обратной матрицейдля квадратной матрицы А порядка n называется матрица
. Аналогично, в теории матриц мы уже ввели понятие противоположной матрицы, ее обозначение (– А). Обратной матрицейдля квадратной матрицы А порядка n называется матрица 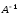 , если выполняются равенства
, если выполняются равенства
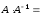
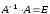 , (1)
, (1)
где Е – единичная матрица порядка n.
Сразу же отметим, что обратная матрица существует только для квадратных невырожденных матриц.
Квадратная матрица называется невырожденной(неособенной), если det A ≠ 0. Если же det A = 0, то матрица А называется вырожденной(особенной).
Отметим, что невырожденная матрица А имеет единственную обратную матрицу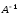 . Докажем это утверждение.
. Докажем это утверждение.
Пусть для матрицы А существует две обратные матрицы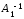 ,
,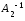 , то есть
, то есть
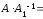
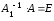 и
и 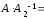
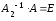 .
.
Тогда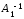 =
=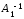 ּ
ּ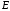 =
=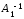 ּ
ּ
(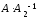 ) =
) =
= ( ּ
ּ )
)  =
=
 =
=

 =
= .
.
Что и требовалось доказать.
Найдем определитель обратной матрицы. Так как определитель произведения двух матриц А и В одинакового порядка равен произведению определителей этих матриц, т. е. , следовательно, произведение двух невырожденных матриц АВ есть невырожденная матрица.
, следовательно, произведение двух невырожденных матриц АВ есть невырожденная матрица.
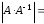
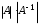 =
=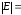 1
1 
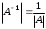 .
.
Делаем вывод, что определитель обратной матрицы есть число, обратное определителю исходной матрицы.
2. АЛГОРИТМ ПОСТРОЕНИЯ ОБРАТНОЙ МАТРИЦЫ.
СВОЙСТВА ОБРАТНОЙ МАТРИЦЫ
Покажем, что, если матрица А невырожденная, то для нее существует обратная матрица, и построим ее.
Пусть
А=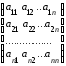 ,
, 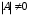 .
.
Составим матрицу из алгебраических дополнений элементов матрицы А:
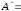
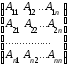
Транспонируя ее, получим так называемую присоединеннуюматрицу:
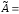
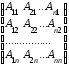 .
.
Найдем произведение ּ
ּ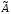 . С учетом теоремы Лапласа и теоремы аннулирования:
. С учетом теоремы Лапласа и теоремы аннулирования:
 ּ
ּ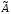
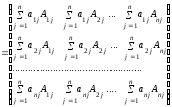
= =
=
=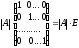

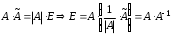 .
.
Делаем вывод:
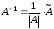 . (2)
. (2)
Алгоритм построения обратной матрицы.
Пример. Найти обратную матрицу.
а). Пусть А=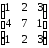 . Так как матрица А имеет две одинаковые строки, то определитель матрицы равен нулю. Следовательно, матрица вырожденная, и для нее не существует обратной матрицы.
. Так как матрица А имеет две одинаковые строки, то определитель матрицы равен нулю. Следовательно, матрица вырожденная, и для нее не существует обратной матрицы.
б). Пусть А=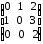 .
.
Вычислим определитель матрицы
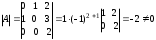
 обратная матрица существует.
обратная матрица существует.
Составим матрицу из алгебраических дополнений
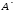 =
= 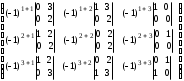 =
= 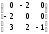 ;
;
транспонируя матрицу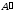 , получим присоединенную матрицу
, получим присоединенную матрицу 

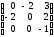 ;
;
по формуле (2) найдем обратную матрицу
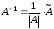 =
=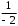
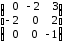
=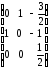 .
.
Проверим правильность вычислений


 =
=
=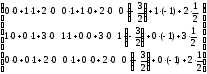 =
= 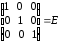 .
.
Следовательно, обратная матрица построена верна.
Свойства обратной матрицы
1.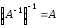 ;
;
2.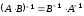 ;
;
3.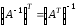 .
.
4. ЗАДАЧИ И УПРАЖНЕНИЯ
4.1 Матрицы и действия над ними
а)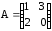 ,
, 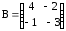 ;
;
б)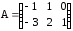 ,
, 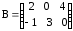 ;
;
в)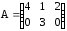 ,
, 
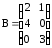 ;
;
г)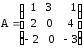 ,
, 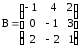 ;
;
д)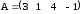 ,
, 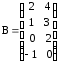 ;
;
е)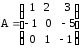 ,
, 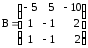 ;
;
ж)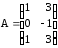 ,
, 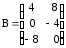 ;
;
з)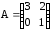 ,
, 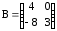 ;
;
и)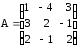 ,
, 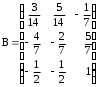 .
.
а)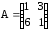 ,
, 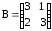 ; б)
; б) 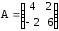 ,
, 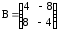
.
а)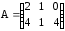 ,
, 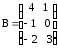 ,
, 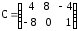 ;
;
б)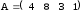 ,
, 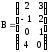 ,
, 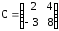 .
.
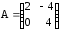 ,
, 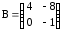 ,
, 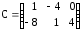 .
.
а)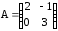 ; б)
; б) 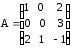 .
.
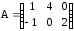 ,
, 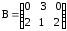 .
.
а)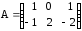 ,
, 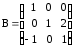 ,
, 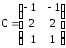 ;
;
б)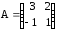 ,
, 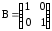 ,
, 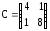 .
.
б) произведения АВ и ВА не существуют;
в)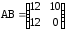 ,
, 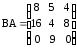 ;
;
г)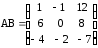 ,
, 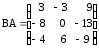 ;
;
д) суммы, разности и произведения ВА матриц не существуют,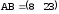 ;
;
е)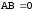 ,
, 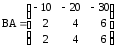 ;
;
ж) произведения матриц не существуют;
з)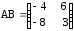 ,
, 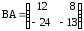
ЛЕКЦИЯ 3. ОБРАТНАЯ МАТРИЦА
План
-
Понятие обратной матрицы. Единственность обратной матрицы. -
Алгоритм построения обратной матрицы.
Свойства обратной матрицы.
-
ПОНЯТИЕ ОБРАТНОЙ МАТРИЦЫ.
ЕДИНСТВЕННОСТЬ ОБРАТНОЙ МАТРИЦЫ
В теории чисел наряду с числом
 определяют число, противоположное ему (
определяют число, противоположное ему (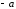 ) такое, что
) такое, что 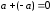 , и число, обратное ему
, и число, обратное ему 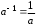 такое, что
такое, что 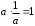 . Например, для числа 5 противоположным будет число
. Например, для числа 5 противоположным будет число (– 5), а обратным будет число
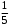 . Аналогично, в теории матриц мы уже ввели понятие противоположной матрицы, ее обозначение (– А). Обратной матрицейдля квадратной матрицы А порядка n называется матрица
. Аналогично, в теории матриц мы уже ввели понятие противоположной матрицы, ее обозначение (– А). Обратной матрицейдля квадратной матрицы А порядка n называется матрица 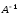 , если выполняются равенства
, если выполняются равенства 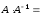
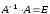 , (1)
, (1)где Е – единичная матрица порядка n.
Сразу же отметим, что обратная матрица существует только для квадратных невырожденных матриц.
Квадратная матрица называется невырожденной(неособенной), если det A ≠ 0. Если же det A = 0, то матрица А называется вырожденной(особенной).
Отметим, что невырожденная матрица А имеет единственную обратную матрицу
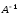 . Докажем это утверждение.
. Докажем это утверждение.Пусть для матрицы А существует две обратные матрицы
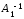 ,
,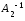 , то есть
, то есть 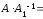
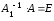 и
и 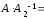
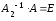 .
. Тогда
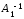 =
=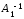 ּ
ּ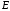 =
=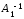 ּ
ּ
(
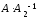 ) =
) = = (
 ּ
ּ )
)  =
=
 =
=

 =
= .
. Что и требовалось доказать.
Найдем определитель обратной матрицы. Так как определитель произведения двух матриц А и В одинакового порядка равен произведению определителей этих матриц, т. е.
 , следовательно, произведение двух невырожденных матриц АВ есть невырожденная матрица.
, следовательно, произведение двух невырожденных матриц АВ есть невырожденная матрица.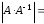
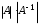 =
=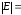 1
1 
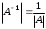 .
.Делаем вывод, что определитель обратной матрицы есть число, обратное определителю исходной матрицы.
2. АЛГОРИТМ ПОСТРОЕНИЯ ОБРАТНОЙ МАТРИЦЫ.
СВОЙСТВА ОБРАТНОЙ МАТРИЦЫ
Покажем, что, если матрица А невырожденная, то для нее существует обратная матрица, и построим ее.
Пусть
А=
 ,
, 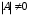 .
.Составим матрицу из алгебраических дополнений элементов матрицы А:
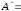

Транспонируя ее, получим так называемую присоединеннуюматрицу:
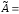
 .
.Найдем произведение
 ּ
ּ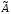 . С учетом теоремы Лапласа и теоремы аннулирования:
. С учетом теоремы Лапласа и теоремы аннулирования: ּ
ּ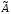
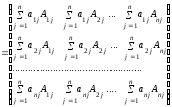
=
 =
==
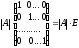

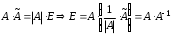 .
.Делаем вывод:
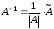 . (2)
. (2)Алгоритм построения обратной матрицы.
-
Вычислить определитель матрицы А. Если определитель равен нулю, то обратной матрицы не существует. -
Если определитель матрицы не равен нулю, то составить из алгебраических дополнений соответствующих элементов матрицы А матрицу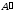 .
. -
Транспонируя матрицу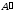 , получить присоединенную матрицу
, получить присоединенную матрицу  .
. -
По формуле (2) составить обратную матрицу .
. -
По формуле (1) проверить вычисления.
Пример. Найти обратную матрицу.
а). Пусть А=
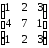 . Так как матрица А имеет две одинаковые строки, то определитель матрицы равен нулю. Следовательно, матрица вырожденная, и для нее не существует обратной матрицы.
. Так как матрица А имеет две одинаковые строки, то определитель матрицы равен нулю. Следовательно, матрица вырожденная, и для нее не существует обратной матрицы.б). Пусть А=
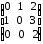 .
.Вычислим определитель матрицы
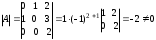
 обратная матрица существует.
обратная матрица существует.Составим матрицу из алгебраических дополнений
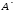 =
= 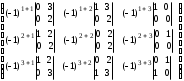 =
= 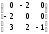 ;
;транспонируя матрицу
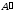 , получим присоединенную матрицу
, получим присоединенную матрицу 

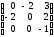 ;
;по формуле (2) найдем обратную матрицу

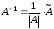 =
=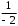
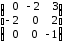
=
 .
.Проверим правильность вычислений


 =
==
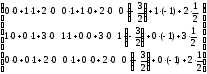 =
= 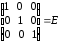 .
.Следовательно, обратная матрица построена верна.
Свойства обратной матрицы
1.
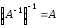 ;
;2.
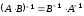 ;
;3.
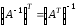 .
.4. ЗАДАЧИ И УПРАЖНЕНИЯ

4.1 Матрицы и действия над ними
-
Найти сумму, разность, произведения двух матриц А и В.
а)
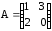 ,
, 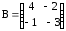 ;
; б)
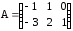 ,
, 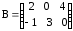 ;
;в)
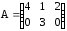 ,
, 
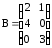 ;
; г)
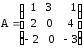 ,
, 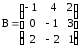 ;
;д)
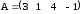 ,
, 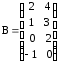 ;
; е)
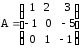 ,
, 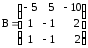 ;
;ж)
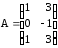 ,
, 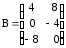 ;
; з)
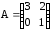 ,
, 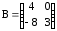 ;
;и)
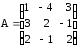 ,
, 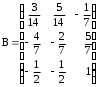 .
.-
Доказать, что матрицы А и В коммутирующие.
а)
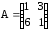 ,
, 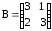 ; б)
; б) 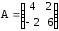 ,
, 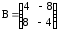
.
-
Даны матрицы А. В и С. Показать, что (АВ)·С=А·(ВС).
а)
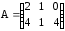 ,
, 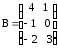 ,
, 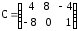 ;
;б)
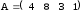 ,
, 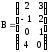 ,
, 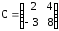 .
.-
Вычислить (3А – 2В)·С, если
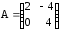 ,
, 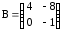 ,
, 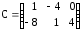 .
.-
Найти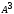 , если
, если
а)
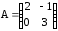 ; б)
; б) 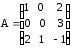 .
.-
Найти матрицу Х, если 3А+2Х=В, где
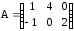 ,
, 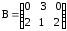 .
.-
Найти АВС, если
а)
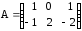 ,
, 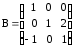 ,
, 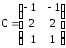 ;
;б)
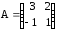 ,
, 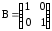 ,
, 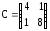 .
.ОТВЕТЫ ПО ТЕМЕ «МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ»
-
а)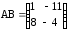 ,
, 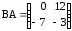 ;
;
б) произведения АВ и ВА не существуют;
в)
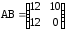 ,
, 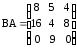 ;
;г)
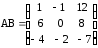 ,
, 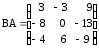 ;
;д) суммы, разности и произведения ВА матриц не существуют,
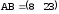 ;
;е)
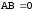 ,
, 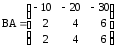 ;
;ж) произведения матриц не существуют;
з)
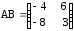 ,
,