Файл: Лекция матрицы план Понятие матрицы. Типы матриц. Алгебра матриц.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.12.2023
Просмотров: 106
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

 –
– 

 ,
, (2)
т. е. каждое слагаемое в формуле (2) представляет собой произведение элементов определителя, взятых по одному и только одному из каждой строки и каждого столбца. Чтобы запомнить, какие произведения в формуле (2) брать со знаком плюс, а какие со знаком минус, полезно знать правило треугольников (правило Саррюса):

Пример. Вычислить определитель
 =
=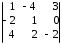 =
==
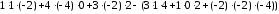 =
==
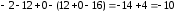 .
.Следует отметить, что свойства определителя второго порядка, рассмотренные выше, без изменений переносятся на случай определителей любого порядка, в том числе и третьего.
2. ТЕОРЕМЫ ЛАПЛАСА И АННУЛИРОВАНИЯ
Рассмотрим еще два очень важных свойства определителей.
Введем понятия минора и алгебраического дополнения.
Минором элемента определителя называется определитель, полученный из исходного определителя вычеркиванием той строки и того столбца, которым принадлежит данный элемент. Обозначают минор элемента
 через
через 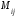 .
.Пример.
 =
=  .
. Тогда, например,
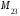 =
=  ,
, 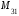 =
= 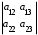 .
.Алгебраическим дополнением элемента
 определителя
определителя  называется его минор
называется его минор 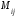 , взятый со знаком
, взятый со знаком 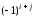 . Алгебраическое дополнение будем обозначать
. Алгебраическое дополнение будем обозначать
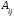 , то есть
, то есть 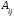 =
=
 .
.Например:
 =
=  ,
, 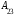 =
=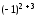
 =
=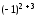
 = –
= – ,
,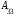 =
=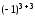
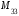 =
=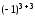
 =
= .
.Вернемся к формуле (2). Группируя элементы и вынося за скобки общий множитель, получим:
 =
= (
(
 –
– 
 ) +
) + (
(
 –
– 
 ) +
) + (
(
 –
–
 )=
)==
 ּ
ּ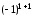
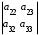 +
+
ּ
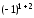
 +
+ ּ
ּ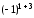
 =
==

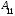 +
+
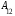 +
+
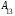 .
.Аналогично доказываются равенства:
 =
=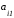
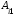 +
+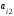
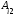 +
+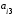
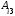 ,
,  1, 2, 3; (3)
1, 2, 3; (3) =
=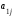
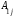 +
+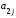
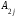 +
+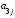
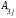 ,
, 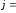 1, 2, 3.
1, 2, 3.Формулы (3) называются формулами разложения определителя по элементам i-ой строки (j-го столбца), или формулами Лапласа для определителя третьего порядка.
Таким образом, мы получаем восьмое свойство определителя:
Теорема Лапласа. Определитель равен сумме всех произведений элементов какой-либо строки (столбца) на соответствующие алгебраические дополнения элементов этой строки (столбца).
Заметим, что данное свойство определителя есть не что иное, как определение определителя любого порядка. На практике его используют для вычисления определителя любого порядка. Как правило, прежде чем вычислять определитель, используя свойства 1 – 7, добиваются того, если это возможно, чтобы в какой-либо строке (столбце) были равны нулю все элементы, кроме одного, а затем раскладывают по элементам строки (столбца).
Пример. Вычислить определитель
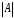 =
=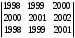 = (из второй строки вычтем первую) =
= (из второй строки вычтем первую) ==
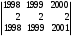 = (из третьей строки вычтем первую)=
= (из третьей строки вычтем первую)==
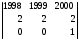 = (разложим определитель по элементам третьей
= (разложим определитель по элементам третьей строки) = 1ּ

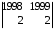 = (из второго столбца вычтем первый столбец) =
= (из второго столбца вычтем первый столбец) = 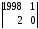 = 1998ּ0 – 1ּ2 = –2.
= 1998ּ0 – 1ּ2 = –2.Пример.
Рассмотрим определитель четвертого порядка. Для его вычисления воспользуемся теоремой Лапласа, то есть разложением по элементам строки (столбца).
 =
= = (так как второй столбец содержит три нулевых элемента, то разложим определитель по элементам второго столбца)= =3ּ
= (так как второй столбец содержит три нулевых элемента, то разложим определитель по элементам второго столбца)= =3ּ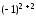
 = (из второй строки вычтем первую, умноженную на 3, а из третьей строки вычтем первую, умноженную на 2) =
= (из второй строки вычтем первую, умноженную на 3, а из третьей строки вычтем первую, умноженную на 2) = = 3ּ
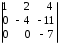 = (разложим определитель по элементам первого столбца) = 3ּ1ּ
= (разложим определитель по элементам первого столбца) = 3ּ1ּ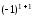
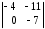 =
= 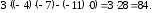
Девятое свойство определителя носит название теорема аннулирования:
сумма всех произведений элементов одной строки (столбца) определителя на соответствующие алгебраические дополнения элементов другой строки (столбца) равна нулю, то есть
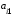
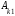 +
+
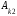 +
+
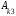 = 0,
= 0, 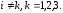
Пример.
 =
= 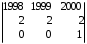 = (разложим по элементам третьей строки)=
= (разложим по элементам третьей строки)== 0ּ
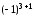
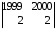 +0ּ
+0ּ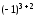
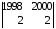 +
+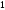 ּ
ּ
 = –2.
= –2.Но, для этого же примера: 0ּ
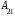 +0ּ
+0ּ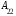 +1ּ
+1ּ =
== 0ּ
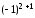
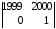 +0ּ
+0ּ
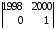 +1ּ
+1ּ
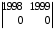 = 0.
= 0.Если определитель любого порядка имеет треугольный вид
 =
=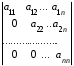 , то он равен произведению элементов, стоящих на диагонали:
, то он равен произведению элементов, стоящих на диагонали:  =
= ּ
ּ ּ … ּ
ּ … ּ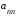 . (4)
. (4)Пример. Вычислить определитель.
 =
=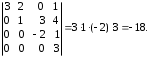
Иногда при вычислении определителя с помощью элементарных преобразований удается свести его к треугольному виду, после чего применяется формула (4).
Что касается определителя произведения двух квадратных матриц, то он равен произведению определителей этих квадратных матриц: