Файл: Реферат Высшая математика Нахождение производных функций одной переменной, заданных параметрически.docx

Скачать файл (0,17Мб)

Заказать решение

ВУЗ: Не указан

Категория: Реферат

Дисциплина: Не указана

Добавлен: 07.12.2023

Просмотров: 115

Скачиваний: 3

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

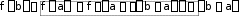– другая редакция формулы Лагранжа.
Замечание3

^Точекc^может^быть^{несколько.}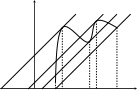

ac₁c₂c₃b
Замечание4

Если

fa fb^,^то

f^c  0 ^–^{утверждение}^{теоремы}^Ролля.

Замечание5

Теорему Лагранжа можно использовать для приближенных вычислений.

fb fa 

f^a b ab a^,

0    1.

Положим

  ¹, тогда

2

fb 

fa 

f^^^a^^b^b a.

_₂_

Погрешность тем меньше, чем ближе bк a.

Пример

b 1,1,

a 1,0 ,

^arctg1,1– ?

1 2 3 4 5 6 7 8 9

arctg1,1  arctg1  0,1 arctg x^

,

xc

^arctg x^^¹,

1  x²

_c_1,0 1,1 _,

2

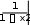_c_2,1

2

_1

2,1
 0,5 ^,

arctg1,1 

^ 0,05 .

4

Если

Теорема Коши

ТеоремаКоши

fx^,^^^x^^–^{непрерывны}^на^^a^,^b^^;

²⁾f^x^,^^^^x^^на^^a^,^b^^;

3) ^^^^x^^⁰

то

^^x^^^a^,^b^,

^^c^^^a^,^b^:
Доказательство

^^^b^^^^^a^, так как иначе по теореме Ролля

^x

обращалась бы в

нуль, по крайней мере, в одной точке

^c^^^a^,^b^.

Рассмотрим вспомогательную функцию:

Fx 

fx 

fa ^f^^b^^^f^^a^x  a.

   
 b  a

Она удовлетворяет всем условиям теоремы Ролля 

^^c^^^a^,^b^такая, что ^F^^^c^^⁰

   
f^c ^f^^b^^^f^^a^ ^c.

 b  a

Разделим равенство на

^^^^c^с учетом того, что

^^^^c^^⁰:

^f^^b^^^f^^a^^f^^^c^, что и требовалось доказать.

b  a ^c

Замечание

Теорема Лагранжа является частным случаем теоремы Коши.

Смотрите также файлы

Эссе по психологии.docx

Интерактивные методы обучения на уроках истории.docx

Рекомендованные фразы и выражения для написания дневника пп в поликлиники.docx

Контрольная работа по дисциплине Методы принятия управленческих решений Темы.docx

Вопросы экзаменационных билетов.doc

Файл: Реферат Высшая математика Нахождение производных функций одной переменной, заданных параметрически.docx

arctg1,1  arctg1  0,1 arctg x^

Теорема Коши

Смотрите также файлы

Информация

Списки файлов

Дополнительно

Файл: Реферат Высшая математика Нахождение производных функций одной переменной, заданных параметрически.docx

arctg1,1  arctg1  0,1 arctg x

Теорема Коши

Смотрите также файлы

Информация

Списки файлов

Дополнительно

arctg1,1  arctg1  0,1 arctg x^