Файл: Реферат Высшая математика Нахождение производных функций одной переменной, заданных параметрически.docx

Сделать презентацию

Скачать файл (0,17Мб)

Заказать решение

ВУЗ: Не указан

Категория: Реферат

Дисциплина: Не указана

Добавлен: 07.12.2023

Просмотров: 362

Скачиваний: 3

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Федеральное государственное бюджетное образовательное учреждение высшего образования «Санкт-Петербургский университет Государственной противопожарной службы Министерства РФ по делам гражданской обороны, чрезвычайным ситуациям и ликвидации последствий стихийных бедствий

имени Героя Российской Федерации генерала армии Е.Н. Зиничева»

Кафедра высшей математики системного моделирования сложных процессов

Реферат
Высшая математика
Нахождение производных функций одной переменной, заданных параметрически

Выполнил обучающийся
Группа

Проверил преподаватель

Санкт-Петербург

2022

ОГЛАВЛЕНИЕ1. ПРОИЗВОДНАЯ ФУНКЦИИ 1.1. Определение производной функции 1.2. Односторонние производные функции 2. ДИФФЕРЕНЦИАЛ ФУНКЦИИ 2.1. Определение дифференциала функции 2.2. Дифференциал независимой переменной 3. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙИ ДИФФЕРЕНЦИАЛА 3.1. Геометрический смысл производной 3.2. Геометрический смысл дифференциала 3.3. Приближенное вычисление малых приращений функции 4. ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ. ПРОИЗВОДНЫЕЭЛЕМЕНТАРНЫХ ФУНКЦИЙ 4.1. Свойства производных (правила дифференцирования) 4.2. Производная обратной функции 4.3. Производные элементарных функций 5. ДИФФЕРЕНЦИРОВАНИЕ СЛОЖНОЙ ФУНКЦИИ, ФУНКЦИИ, ЗАДАННОЙ НЕЯВНО И ПАРАМЕТРИЧЕСКИ 5.1. Производная сложной функции 5.2. Производная неявной функции 5.3. Логарифмическая производная 5.4. Производная функции, заданной параметрически 6.ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХПОРЯДКОВ6.1. Производные высших порядков 6.2. Дифференциалы высших порядков 7.ОСНОВНЫЕ ТЕОРЕМЫ ДИФФЕРЕНЦИАЛЬНОГОИСЧИСЛЕНИЯ 7.1. Теорема Ролля 7.2. Теорема Лагранжа 7.3. Теорема Коши

ПРОИЗВОДНАЯ ФУНКЦИИ

Определение производной функции.
Односторонние производные.

Определение производной функции

Рассмотримследующуюзадачу,которая

позволит лучше понять смысл производной.

Материальная точка совершает прямолинейное неравномерное движение.

Пусть

s₀ ^–^путь,^{пройденный}^за^время

t₀ ^,s^–^путь,^{пройденный}^за^времяt^.

Отрезок пути

s s s₀

точка пройдет за промежуток времени

t t t₀^.

^{Средняя}^{скорость}^на^{интервале}^{времени}^отt₀

s, равна:

^доt^,^или^на^{участке}^пути

v ^^s^.

ср __t

Средняя скорость зависит от

t. При уменьшении t

соответствующий

промежуток пути s

^{времени}t₀ ^:

уменьшается. Мгновенная скорость движения в момент

v lim

s_.

t0 __t

Перейдем к определению понятия производной.

Рассмотрим функцию

fx^,^{определенную}^на^{интервале}^^a^,^b^^,

^x^^^a^,^b^–

фиксированная точка. Число x

таково, что точка

^x^^^x^^^a^,^b^.

Отношение

y(x,x)

x

зависит от xи

x.

Определение

Производной функции

приращений
fx
^в^точкеx^{называется}^предел^{отношения}

lim

y_
lim

fxxfx _,

x0 __x

при условии, что он существует.
Обозначение

x0 __x

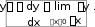
Примеры

^y^^sin^x.

2cos^x ^^x^sin ^^x

sinxxsinx

⁰

 ₂ ₂

y^x 

lim _

 __

lim ^^



 cos x.

x0 _x

⁰

x0 _x

yx  log _ax^,

0  a 1.

y log

x x  log
x log

^1  ^^x^^,

a

 log

a

_₁_x_

_a _x

1

_a 

y^x 

lim

 ^x _^⁰^_

lim

log

^1  ^^x^x 

x0 __x

_₀_

x0 ^a^_x^

 1

 ^x ^x

a _
 

 lim

log

^₁_^^x^^x^

 ¹log e^.

x0

_ _x __x_a

 

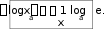
Частный случай при

a e:

Односторонние производные функции

Одностороннимипроизводныминазываютсяодносторонниепределы:^y^⁽^x⁾^^lim^^y– леваяпроизводная вточкеx,^x0__x^y^⁽^x⁾^^lim^^y–праваяпроизводная вточкеx.^x0__x

Для существования производной функции

y f(x)

^{в точке}x

необходимо и достаточно существование и равенство односторонних ^{производных}^{функции в}^точкеx^.

ДИФФЕРЕНЦИАЛ ФУНКЦИИ

Определение дифференциала функции.
Дифференциал независимой переменной.

Определение дифференциала функции

Пусть

y fx ^{дифференцируема}^на^^a^,^b^^.

xa,b
 lim

y _

^f^^^x^

y _

f^x  ,

x0 __x

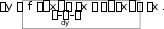 – бесконечно малая при Тогда

x

x 0 .

(*)

Введем обозначение
dy

f^x x^.

В общем случае

f^x  0 

lim

dy_

^f^^^x^

x0 __x

  x ox

– бесконечно малая более высокого порядка малости

чем
x , т. к. Итак,
lim

x0

xx_₀_.

x

Определение

Величина ^в^точкеx^.

dy

f^x x

называется дифференциаломфункции

y fx

Из равенства (*) следует, что ^dy– главнаялинейнаячастьприращения

функции.

Главная, т. к. остаток малости.

x

бесконечно малая более высокого порядка

Смотрите также файлы

Эссе по психологии.docx

Интерактивные методы обучения на уроках истории.docx

Рекомендованные фразы и выражения для написания дневника пп в поликлиники.docx

Контрольная работа по дисциплине Методы принятия управленческих решений Темы.docx

Вопросы экзаменационных билетов.doc

Файл: Реферат Высшая математика Нахождение производных функций одной переменной, заданных параметрически.docx

ПРОИЗВОДНАЯ ФУНКЦИИ

Определение производной функции

Производной функции

Односторонние производные функции

ДИФФЕРЕНЦИАЛ ФУНКЦИИ

Определение дифференциала функции

функции.

Смотрите также файлы

Информация

Списки файлов

Дополнительно