Файл: Реферат Высшая математика Нахождение производных функций одной переменной, заданных параметрически.docx

Скачать файл (0,17Мб)

Заказать решение

ВУЗ: Не указан

Категория: Реферат

Дисциплина: Не указана

Добавлен: 07.12.2023

Просмотров: 114

Скачиваний: 3

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

осуществляется через параметр t. Как вычислить
Теорема

y^_x^?

Если

1)
^x^^t^,
yt
дифференцируемы ( ^^x^^^t^,
y^t⁾^на^{интервале}^^^,^^^,^и
xt

строго монотонна на ^^^,^^;

2) ^x^^^t^^⁰

то

^^t^^^^,^^,

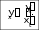
Доказательство

Рассмотрим систему равенств

y yt^,^t^^t^^x^^,где t– промежуточный аргумент,

y– сложная функция аргумента x.

По теореме о производной сложной функции производной обратной функции
y^_x
 y_t^ t^_x^.^П^о^тео^р^еме^о

t
t^ ¹.

Таким образом,

^x x^

y^ ^y^t^, что и требовалось доказать.

t
^x x^

Пример

^_x t² ,

3


^_y t ,
^t^^^^^,0^.

y^_x^–^?

Решениеx_t^ 2t ^,y_t^ 3t² ,

y^ ³t.

x ₂

ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ

Производные высших порядков.
Дифференциалы высших порядков.

Производные высших порядков

Определение

f^x   f^x^

втораяпроизводная– первая производная от производной

первого порядка;

f^ⁿ^x  f^ⁿ^¹^x^

производная n-гопорядка– первая производная от

производной ^ⁿ^¹^-го порядка.
Примеры

^y^^sin^x.

y^ cos x ^,y^ sin x ^,y^ cos x^.

y xⁿ.

y^ n xⁿ^¹ ,

y^ nn1xⁿ^² ,

…

y^^k^ nn1...n k1xⁿ^^k

( k n).

y e^x.

y^ⁿ^ e^x.

Вторая производная от неявной функции

^Пусть^{неявная}^{функция}y^{аргумента}x^{задается равенством}
Fx, y  0^.

Правило

Для отыскания высшей производной от yпо x , нужно соответствующее число раз дифференцировать заданное равенство, помня, что yи все ее производные являются функциями независимой переменной x.

Пример

y²  x²  1.

y^^{– ?}

2y y^ 2x 0 

y^  ^x,

y

2y

^²
 2y y^
 2  0 
y^ 

1  y^²y

__x²  y²

.
_y3

Вторая производная функции, заданной параметрически

Рассмотрим функцию y, заданную параметрическим способом

_x xt ,


^y yt.

Выше была получена формула для первой производной этой функции

y^_x

_y^t_.

x^t

Новая задача – вычисление второй производной

y^_x^_x^{– ?}

y^t^

y^ x^ y^ x^1

y^ x^ y^ x^

y^_x^_x

^^^y^_x^^'^x^_____t^^t^_x^^t

t t t _t


2 _

t t t

.
3

_xt_

x_t^ ^x_t

x_t^

Пример

^x^^a^^t^^sin^t^,
y a1 cost^,
   t .

y^_x^–^?

y^_x^_x^–^?


y^_x
a sin ta1  cost ^,

t


 __

^ctg_₂_

xx

a1  cos t
y^ ^_

^^__.

Дифференциалы высших порядков

Дифференциал независимой переменной, как было показано выше, равен

ее приращению

dx x, которое независитотx!

Дифференциал функции

dy

f^xdx

при фиксированном dx– зависит

от аргумента x , то есть является функцией. Поэтому можно поставить вопрос о дифференциале этой функции или дифференциале дифференциала.

Дифференциал дифференциала функции – второй дифференциал функции или дифференциал второго порядка.

Определения и обозначения

d² fx  ddfx – дифференциал второго порядка;

d³ fx  dd² fx – дифференциал третьего порядка;

…

dⁿfx  ddⁿ^¹ fx – дифференциал n-го порядка.