Файл: Реферат Высшая математика Нахождение производных функций одной переменной, заданных параметрически.docx

Скачать файл (0,17Мб)

Заказать решение

ВУЗ: Не указан

Категория: Реферат

Дисциплина: Не указана

Добавлен: 07.12.2023

Просмотров: 113

Скачиваний: 3

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Линейная, т. к. ^dyпропорционален xв первой степени.
Теорема

Необходимым и достаточным условием существования дифференциала является существование производной функции.

Дифференциал независимой переменной

Рассмотрим
Вывод

y x^,

y^_x 1^,

y x

 ^dy^^^x

(см. (*)).

dx x

приращению.

 ^{дифференциал независимой переменной равен ее}

С учетом полученного:

dy y^_x x y^_x dx^.

– формула для вычисления первого дифференциала.

Вывод

Дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.

Отсюда

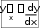
– производная есть отношение дифференциалов.

ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ

И ДИФФЕРЕНЦИАЛА

Геометрический смысл производной.
Геометрический смысл дифференциала.
Приближенное вычисление малых приращений функции.

Геометрический смысл производной

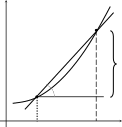
Рассмотрим график функции

y fx^.

fx₀  x_P
y


fx₀ _M
x₀x₀ x

x

Точки графика секущей MP.

Определение

Px₀  x, fx₀  x^,

Mx₀, fx₀ 

принадлежат

Касательнойк графику

y fx

в точке

x₀ ^{называется}^{предельное}

положение секущей при

Теорема

x 0

( P M).

Еслифункция

y fx ^имеет^в^точке

x₀ ^{производную}

f^x₀^,

то график функции в точке

f^x₀ ^.

Доказательство

x₀ ^имеет^{касательную}^с^{угловым}^{коэффициентом}

Угловой коэффициент секущей равен

tg   ^^y.

x

Если
x 0 , то

tg   lim

y_

f^x.

x0 __x⁰

Таким образом:

существует предельное положение секущей;

^kкасат^

f^x₀ ^.

Уравнение касательной к графику функции в точке

Mx₀, fx₀

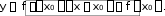
Определение

Нормальюк графику функции
fx ^в^точке
x₀ ^{называется}^{прямая,}^{проходящая}

через точку

Mx₀, fx₀ ^пе^р^п^е^н^д^и^к^у^л^я^р^но^к^асател^ь^н^о^{й в}^э^т^о^й^т^о^ч^ке.

Угловой коэффициент нормали связан с угловым коэффициентом касательной:

k_н 

1 _.

f^x₀

Уравнение нормали к графику функции в точке

Mx₀, fx₀ ^:

Пример

Составить уравнения касательной и нормали к графику функции

y ln x

в точке

x 1.

Решение

y1  0 ^.

y^ ¹,

x

y^1  1^.

y x 1
– уравнение касательной.

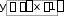– уравнение нормали.

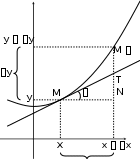
Геометрический смысл дифференциала

Рассмотрим график функции

M^x x, y y^.

y fx^{. Точки графика}^–

Mx, y^,

x
MT– касательная к графику в точке M.

В треугольнике

MNT:

MN x,

NT x tg   x y^_x^.^Таким^{образом}

Вывод

Дифференциал функции
y fx
в точке x есть приращение ординаты

касательной к графику этой функции, когда xполучает приращение x.

Приращение функции

NM^ y NT^.

Для вогнутой кривой (выпуклой вниз)

^^y^^dy.

Для выпуклой кривой (выпуклой вверх)

^^y^^dy.

Для линейной функции

^y^^ax^^b:

^^y^^dy.

Пример

Рассмотрим функцию
y  x² .

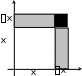
y x x² x² .

y 2x x x².

^dy^²^x^^^x.

^^y– площадь окрашенной части квадрата, ^dy– та же площадь за

вычетом x².

Если

x 20,

^^x^^0,1,
y 2  20  0,1  0,1² 4,01.

^dy^²^²⁰^^0,1^^4,00.

Итак, ^^y

и ^dyотличаются на величину

^^^0,01, что существенно

меньше x.

Приближенное вычисление малых приращений функции

Если x

мало, то

fx  dfx^.

Геометрический смысл приближенного равенства: данная функция на

участке xзаменяется своей касательной, то есть, линейной функцией.
Примеры

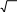Вычислить приближенно ³1,1 .

Решение

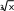y ,

x 1,

^^x^^0,1.

yx x ^–^?

yx x  yx  y^xx

Смотрите также файлы

Эссе по психологии.docx

Интерактивные методы обучения на уроках истории.docx

Рекомендованные фразы и выражения для написания дневника пп в поликлиники.docx

Контрольная работа по дисциплине Методы принятия управленческих решений Темы.docx

Вопросы экзаменационных билетов.doc

Файл: Реферат Высшая математика Нахождение производных функций одной переменной, заданных параметрически.docx

Дифференциал независимой переменной

ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ

И ДИФФЕРЕНЦИАЛА

Геометрический смысл производной

Геометрический смысл дифференциала

Приближенное вычисление малых приращений функции

Смотрите также файлы

Информация

Списки файлов

Дополнительно