Файл: Реферат Высшая математика Нахождение производных функций одной переменной, заданных параметрически.docx

Скачать файл (0,17Мб)

Заказать решение

ВУЗ: Не указан

Категория: Реферат

Дисциплина: Не указана

Добавлен: 07.12.2023

Просмотров: 117

Скачиваний: 3

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Пусть

fx  x^,^тогда

f^x  0

^d²x 0 ^.

f^x 0 ^

d³x 0 ^и^так^далее.

Вывод

Дифференциалы высших порядков от независимой переменной равны нулю.

ОСНОВНЫЕ ТЕОРЕМЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
1. Теорема Ролля.
2. Теорема Лагранжа.
3. Теорема Коши.

Если

Теорема Ролля

ТеоремаРолля(онулепроизводной)

fx ^–^{непрерывна}^на^^a^,^b^^;

²⁾f^x ^на^^a^,^b^^;

³⁾fa fb^,

то ^^^a^,^b^:

^* Подчеркнем, что

dx²  dx².

Доказательство

Так как

fx ^{непрерывна}^на^^a^,^b^^,^она^{достигает}^на^^a^,^b^^{наибольшего}

M^и^{наименьшего}m^{значений.}^{Возможны}^{два случая.}

M m.

Тогда

fx M m^

f x ^–const^.

f^x 0 ^.

M m.

Тогда хотя бы одно из этих значений достигается внутри ^^a^,^b^, то есть

в точке Пусть

^^^a^,^b^,так как

f   M^,^где

fa fb^.

^^^^a^,^b^. Так как  – внутренняя точка,

^тоf^^.

Докажем, что

f^  0^.

f ^ 
lim

x0

fxf_.

x

f

f  x

x.
lim

x00
fxf _

x

^fп^рав
  0 , (*)

lim

x00

fxf _

x

^fл^ев

  0. (**)

Но из существования

f^

следует, что

f ^ 

f_п^_рав 

f_л^_ев^^

f^  0

с учетом (*) и (**), что и требовалось доказать. Аналогично

выполняется доказательство для

f m^{. Теорема}^{доказана.}

Геометрическая интерпретация

Если функция удовлетворяет условиям теоремы Ролля на отрезке ^^a^,^b^, то в некоторой точке отрезка ее касательная параллельна оси OX.

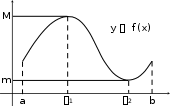
Теорема Ролля позволяет узнать об обращении производной в нуль без ее вычисления.

Пример

fx  xx1x 2x 3^.

Доказать, что все корни уравнения

^^^3,0^.

Доказательство

f ^x  0

принадлежат интервалу

f0 

f1 

f 2 

f 3  0 ^.

Для каждого из отрезков ^^^3,^²^, ^^^2,^¹^, ^^^1,0^

выполняются

условия теоремы Ролля, следовательно, есть три точки, по одной на каждом из соответствующих интервалов, в которых производная обращается в нуль.

Замечание

Все условия теоремы Ролля необходимы для справедливости ее утверждения.

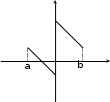
Непрерывностьна ^^a^,^b^.

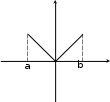
Дифференцируемостьна ^^a^,^b^.

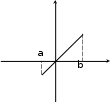
Равенство

fa 

fb^.

Если

Теорема Лагранжа

ТеоремаЛагранжа

fx ^–^{непрерывна}^на^^a^,^b^^;

²⁾f^x ^–^на^^a^,^b^^,

то

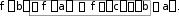
 ca,b^:

Доказательство
Введем обозначение

fbfa __Q_.

b a

Рассмотрим вспомогательную функцию

Fx

fx

fa Qx a^.

Функция

1)

2)

3)

^F^^x^удовлетворяет всем условиям теоремы Ролля:

^F^^x^непрерывна на ^^a^,^b^;

^^F^^^x^на ^^a^,^b^;

^F^^a^^^F^^b^^⁰.

Следовательно,

c:

^c^^^a^,^b^,

^F^^^c^^⁰.

Далее

F^x

f^x Q^,

F^c  f^c Q 0^,

f^c  Q^,

fbfa _

b a
f^c, что и требовалось доказать.

Геометрический смысл теоремы Лагранжа

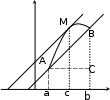
CB_fbfa

угловой коэффициент секущей AB.

x c.

AC

f^c

b a

угловой коэффициент касательной к кривой

y fx
в точке

На дуге ABнайдется, по крайней мере, одна точка M , в которой касательная параллельна хорде AB теорема Ролля является частным случаем теоремы Лагранжа.