Файл: Положение о равномерном распределении молекул в пространстве и равномерном распределении их скоростей по всем направлениям называют.docx

Рис. 3.8. Зависимость относительной концентрации молекул кислорода от высоты при разных температурах T₁ = 300 K и T₂ = 1 300 KВидно, что число частиц в единице объема при большей температуре медленнее убывает с высотой. При уменьшении температуры большая часть частиц располагается на меньшей высоте. А при Т = 0 все частицы расположились бы на поверхности Земли. Этот факт имеет простое физическое объяснение. Каждое конкретное распределение молекул по высоте устанавливается в результате действия двух тенденций:

• 
  притяжение молекул к Земле, характеризуемое потенциальной энергией m₀gh, стремится расположить их на поверхности Земли;
  
• 
  тепловое движение, характеризуемое энергией k_BТ, стремится разбросать молекулы по всем высотам равномерно.
  

Обозначив Е_р = m₀gh, получим

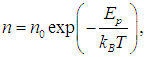(3.53)

то есть концентрация молекул больше там, где меньше их потенциальная энергия. Частицы будут с большей вероятностью располагаться в тех точках пространства, где потенциальная энергия меньше.Больцман доказал, что такое распределение осуществляется в поле любых сил, а не только в гравитационном поле. Поэтому распределение (3.53), где n — концентрация частиц с потенциальной энергией Е_рназывается распределением Больцмана.

---

3.5. Распределение Максвелла — Больцмана

Мы установили функцию, описывающую распределение молекул по скоростям (распределение Максвелла), и зависимость, характеризующую распределение молекул по значениям потенциальной энергии (распределение Больцмана). Обе зависимости можно объединить в одно обобщенное распределение. Рассмотрим бесконечно малый объем dV газа, расположенный в точке с радиусом-вектором   в большой системе, представляющей идеальный газ при постоянной температуре во внешних силовых полях. Число молекул в выделенном объеме есть n(   ) d³r. Поскольку объем невелик, в его пределах плотность частиц можно считать постоянной. Это означает, что выполнено условие справедливости распределения Максвелла. Тогда для числа молекул dN, имеющих скорости от v до v + dv и находящихся в объеме d³r, в результате объединения зависимостей (3.11) и (3.27), получаем следующую формулу:

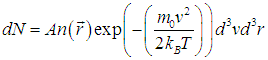(3.54)

 Но концентрация молекул n(r) зависит от расположения этого объема во внешних силовых полях:

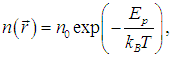(3.55)

где n₀ — концентрация молекул в точке, где Е_p = 0. Тогда

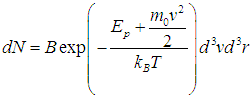(3.56)

Поскольку выражение

(3.57)

---

представляет собой полную энергию частицы во внешнем потенциальном силовом поле, мы приходим к обобщенному распределению Максвелла — Больцмана по энергиям молекул:

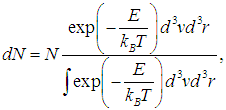(3.58)

 где N — полное число частиц в системе, a dN — число частиц с координатами между r и r + dr и (одновременно) со скоростями между v и v + dv.  Средняя энергия квантового осциллятора. Распределение Максвелла — Больцмана было получено в классической физике, но оно оказалось справедливым и в квантовой механике, где были подвергнуты пересмотру многие казавшиеся незыблемыми положения. В качестве примера рассмотрим задачу о грузе массой т, закрепленном на конце пружинки с жесткостью k. 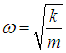Уравнение движения хорошо известно, и его решением являются гармонические колебания тела с круговой частотойКлассическая энергия системы, моделирующей колебания атомов в молекуле дается формулой (3.62) и может принимать любые значения в зависимости от амплитуды колебаний. 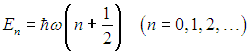Как нам известно из квантовой механики, энергия колебаний квантуется, то есть принимает дискретный ряд значений, определяемых формулой:В соответствии с общими принципами статистической физики вероятность Р_n найти осциллятор в состоянии, характеризуемом неким значением n колебательного квантового числа, определяется формулой

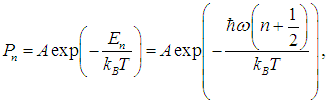(1)

где А — нормировочная постоянная. Для ее определения надо воспользоваться условием нормировки вероятности

---

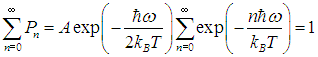(2)

Для этого в известную формулу для геометрической прогрессии

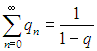(3)

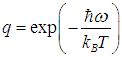
подставим значениеПолучаем тогда вместо (2)

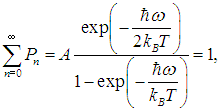(4)

откуда следует выражение для постоянной А. Используя его в выражении (1), приходим к вероятности

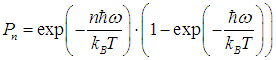(5)

Видно, что чем больше значение квантового числа n, тем меньше вероятность обнаружить осциллятор в таком состоянии. Чем выше температура, тем большие значения n становятся практически значимыми для системы. Прик нулю стремятся все вероятности Р_n с n > 1, и лишьИными словами, при нулевой температуре нет тепловых возбуждений, и осциллятор совершает «нулевые колебания» — находится в основном состоянии с наименьшей энергиейРаспределение осцилляторов по энергиям в зависимости от температуры системы показано на рис. 3.9

---

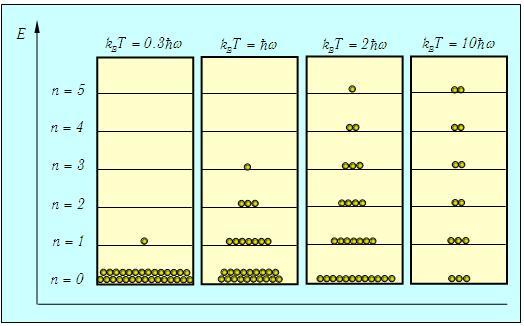
Рис. 3.9. Примерное распределение N = 30 квантовых осцилляторов по энергетическим уровням в зависимости от температуры. Показаны только основной и пять первых возбужденных уровней энергии. При Т = 0 все осцилляторы находятся в основном состоянии. По мере роста температуры становятся доступными все более высокие энергии, и распределение осцилляторов по уровням становится все более равномернымДля наглядности мы взяли систему из небольшого (N = 30) числа осцилляторов (строго говоря, статистические законы применимы к системам с гораздо большим числом частиц). Возникает вопрос: каково среднее значение  колебательного квантового числа n при некоторой температуре T? Для ответа мы должны подсчитать сумму:

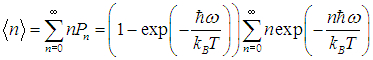(6)

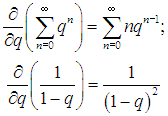
Чтобы сделать это, продифференцируем по q обе части равенства (3.67) для геометрической прогрессии:откуда получаем

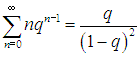(7)

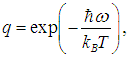
Используя (7) приполучаем из (6) выражение для искомого среднего

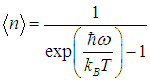(8)

 Теперь легко получить среднюю энергию осциллятора

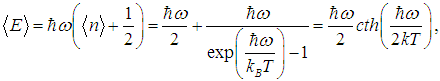(9)

где функция cth — гиперболический котангенс определена соотношением

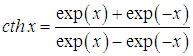(10)

---