Файл: Положение о равномерном распределении молекул в пространстве и равномерном распределении их скоростей по всем направлениям называют.docx

Очевидность полученного результата иллюстрирует высказывание французского математика Лапласа, что теория вероятностей есть здравый смысл, сведенный к математическому исчислению.

Рассмотрим вновь коллектив из ста человек. Здесь мы имеем дело с вероятностями того, что рост индивидуума заключен в определенных пределах. Так, мы знаем вероятность того, что рост находится в пределах от 175 см до 180 см равна 0,15, вероятность того, что рост находится в пределах от 180 см до 185 см равна 0,10, а вероятность того, что рост находится в пределах от 185 см до 190 см равна 0,05. Какова вероятность того, что рост наугад выбранного человека из этого же коллектива превышает 175 см? По закону сложения вероятности приходим к ответу



Аналогично находится вероятность того, что рост будет ниже 175 см:



Зададим теперь вопрос: чему равна вероятность того, что произвольно выбранный индивидуум имеет какой-нибудь рост? Вероятность эта равна единице:



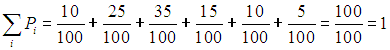
что согласуется с определением вероятности. Мы рассмотрели пример условия нормировки вероятности.

Итак, события, исходы которых принимают непрерывный ряд значений, описываются непрерывной функцией распределения. Для нашего примера с распределением ростов в большом коллективе функцию распределения обозначим w(h). Тогда бесконечно малая величина w(h)dh равна вероятности того, что рост индивидуума заключен в пределах от h до h + dh. Чтобы узнать вероятность P(h₁, h₂), что индивидуум имеет рост в пределах



надо просуммировать все эти бесконечно малые величины, то есть вычислить площадь под частью кривой w(h) между точками с координатами h₁ и h₂

---

:

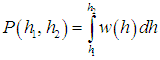(3.3)

Интеграл от функции распределения по всей области ее определения должен быть равен единице, поскольку сумма всех возможных событий является достоверным событием.

Закон умножения вероятностей.

Произведением, (или пересечением), событий А и В называется одновременное осуществление обоих из них.

 

Два события называются независимыми, если наступление одного из них не влияет на вероятность наступления другого.

Для двух независимых событий выполняется закон умножение вероятностей:

(3.4)

Пример 2. Пусть бросаются две игральные кости. Какова вероятность, что сумма чисел на гранях равна 12?

Такой исход возможен при выпадении шестерок на каждой из костей, причем число очков на одной из костей с очевидностью не влияет на число очков на другой. Искомая вероятность равна



Пример 3. Возьмем три коллектива по сто человек в каждом, один из которых состоит исключительно из блондинов, другой — из брюнетов, а третий — из шатенов. Пусть в каждом из них имеется то же самое распределение по росту, что и в рассмотренном выше примере. Перемешаем коллективы и получим новый коллектив из трехсот человек. Ясно, что при таком перемешивании распределение по росту не изменилось, причем рост индивидуума не зависит от цвета его волос. Вероятности того, что индивидуум будет брюнетом, блондином или шатеном равны между собой и равны 1/3. Вопрос: какова вероятность, что наугад выбранный человек окажется брюнетом с ростом в пределах от 175 см до 180 см?

Ответ получается на основе закона умножения вероятностей:

---

Средние величины. Понятие статистического среднего, по сути дела, ничем не отличается от привычного нам понятия среднего арифметического и является его прямым обобщением. В рассматриваемом примере у нас имеется ряд значений роста индивидуума. Под арифметическим средним мы понимаем отношение суммы всех значений некоторой величины к полному их числу, то есть сумму вида



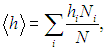
где h_i — значение роста, N_i — число индивидуумов, имеющих это значение роста, N — полное число индивидуумов (измерений).

Статистическое среднее величины h, которое мы будем обозначать через , — это предел отношения   (3.5)

где, соответственно определению, P_i — вероятность того, что величина h имеет значение h_i.

Для случая вычисления среднего роста в рассмотренном выше примере получаем



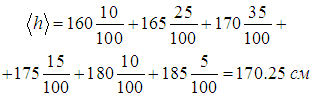
В случае непрерывно распределенных событий мы должны будем вычислить соответствующий интеграл



взятый в пределах всей области изменения переменной h.

3.2. Распределение молекул по скоростям

В этом разделе, являющемся центральным для данной темы, устанавливается вид так называемого распределения Максвелла.

Газ, предоставленный самому себе и находящийся в постоянных внешних условиях, приходит в состояние равновесия. С макроскопической точки зрения в нем устанавливаются постоянная температура и постоянное давление. Если газ состоит из нескольких компонентов (как, например, воздух), то и состав газа в разных местах в сосуде будет одинаков. Молекулы газа даже в равновесии движутся беспорядочно, сталкиваясь между собой и со стенками сосуда, беспрерывно меняя свою скорость.

---

Однако не все столь хаотично, как кажется на первый взгляд. Как бы ни изменялись скорости отдельных молекул, среднее значение квадрата скорости, как это следует из формулы (1.14) молекулярно-кинетической теории идеальных газов) остается постоянным и равным

(3.6)

Зададим вопрос: сколько молекул (или лучше, какая доля молекул) движется с определенной скоростью (смотри ниже о том, что имеется в виду под «с определенной скоростью») в данный момент? Из предположения о хаотическом характере молекулярного движения следует, что возможно появление молекул с любыми скоростями, так что распределение молекул по скоростям надо характеризовать непрерывной функцией. Несмотря на полную хаотичность молекулярных движений, несмотря на случайный характер столкновений и вызываемых ими изменений скоростей молекул, их распределение по скоростям, как показывают теория и опыт, оказывается вполне определенным. На характер распределения по скоростям не влияют даже внешние поля при условии, что состояние системы является равновесным.

Будем считать, что возможные значения скорости заключены в интервале от 0 до бесконечности. В реальных системах скорость не может быть бесконечно большой, так как всякая система состоит из большого, но конечного числа молекул. Поэтому даже если представить себе такой практически невероятный случай, при котором все молекулы остановятся, передав всю энергию одной единственной молекуле, то и тогда энергия этой молекулы и, следовательно, ее скорость будет конечной. Мы здесь даже не говорим об ограничениях, налагаемых теорией относительности, согласно которой скорость любой молекулы не может превысить скорость света. Очень малые и очень большие по сравнению со средним значением скорости мы будем считать в принципе возможными, но, как мы убедимся, они окажутся маловероятными.

Прежде чем приступить к рассмотрению закона распределения молекул газа по скоростям, выясним сущность задачи о распределении. Определить распределение молекул по скоростям, казалось бы, означает определить число молекул, обладающих той или иной заданной скоростью. Однако в такой постановке вопрос не имеет смысла, так как число молекул, имеющих точно (математически точно!) заданную скорость, равно нулю. Действительно, число различных значений скорости бесконечно велико (непрерывное множество), число же молекул конечно.

---

Поэтому число молекул, приходящихся на долю каждого точно заданного значения скорости, равно нулю. Вследствие этого вопрос должен быть сформулирован иначе: сколько молекул (или какая доля молекул) обладает скоростями, лежащими в некотором интервале вблизи заданной скорости?

Итак, найти распределение молекул по скоростям — это означает определить, сколько молекул или какая доля молекул из общего числа N обладают скоростями, лежащими в интервале от v до v + Dv.

Функция распределения молекул по скоростям. В дальнейшем речь, прежде всего, пойдет о распределении вероятностей для вектора скорости  , то есть о том, какова вероятность следующего события: вектор скорости   имеет проекции на оси некоторой декартовой системы координат в пространстве скоростей одновременно принадлежащие следующим интервалам                                                



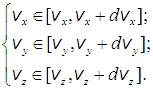
О чем можно сказать и так: конец вектора   находится внутри элемента объема в пространстве скоростей                                               



или: вектор   принадлежит элементу объема  . При использовании в пространстве скоростей не декартовой, а, к примеру, сферической системы координат, изменится лишь набор координат и форма записи элемента объема. При использовании сферической системы координат будем иметь следующее:                                                 



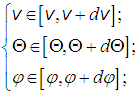
где 

---