Файл: Положение о равномерном распределении молекул в пространстве и равномерном распределении их скоростей по всем направлениям называют.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.12.2023
Просмотров: 104
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
kBТ/2. Три степени свободы поступательного движения молекулы как раз соответствуют полученному здесь результату (3.44). В сущности, именно для того, чтобы получить такое соответствие, мы выбрали должным образом коэффициент α в (3.26 ).
).
Эксперимент по проверке распределения Максвелла. Необходимо еще раз подчеркнуть, что установленный Максвеллом закон распределения молекул по скоростям и все вытекающие из него следствия справедливы только для газа, находящегося в равновесии.
Закон справедлив для любого числа молекул N, если только это число достаточно велико. Закон Максвелла — статистический, а законы статистики выполняются тем точнее, чем к большему числу одинаковых объектов они применяются. При малом числе объектов могут наблюдаться значительные отклонения от предсказанной статистики — флуктуации.
Экспериментальное определение распределения скоростей молекул было осуществлено впервые О. Штерном в 1920 г. Исследовалось распределение по скоростям одноатомных молекул паров металлов (Ag или Pt), из которых была изготовлена нить, расположенная на оси двух цилиндров. Нить нагревалась электрическим током, и металл испарялся (см. рис 3.5).
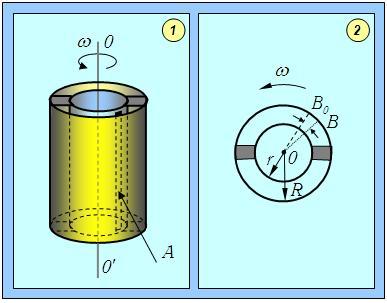
Рис. 3.5 Схема опыта Штерна: 1 — вид установки сбоку; 2 — вид установки сверху
Молекулы, прошедшие через щель во внутреннем цилиндре, летели по прямой и оседали на стенке холодного внешнего цилиндра. Если привести всю установку во вращение (щель все время против точки В0), то молекулы, обладающие большой скоростью v, попадут в некоторую точку вблизи В0, а более медленные затратят на путь больше времени и попадут в точки, отстоящие дальше от В0. Следует обратить внимание, что вылетающие молекулы движутся по прямой, они не участвуют во вращательном движении. Поскольку молекулы в зависимости от скорости попадают в разные точки внешнего цилиндра, то исследуя толщину слоя металла, осевшего на его стенку, можно составить представление о распределении молекул по скоростям.
Найдем распределение молекул по расстояниям S от точки В0 до места их попадания на стенку цилиндра. Если R и r —радиусы большого и малого цилиндров, соответственно (см. рис.), то время полета от щели до стенки цилиндра
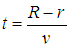
За это время цилиндр повернется на угол
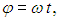
где ω — угловая скорость вращения установки. Соответственно, точка попадания будет смещена относительно В0 на расстояние
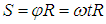
Подставляя сюда время полета, получаем связь скорости молекулы с расстоянием S:
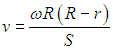
Подставляя, в свою очередь, полученное выражение в распределение Максвелла и учитывая, что
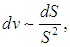
находим распределение молекул по расстояниям S:
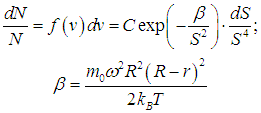
(мы опускаем выражение для нормировочной постоянной С).
Опыты Штерна подтвердили справедливость закона, установленного Максвеллом.
3.4. Распределение молекул по координатам
В этом разделе мы перейдем теперь к анализу распределения молекул газа по координатам. Очевидно, что если на молекулы газа не действуют внешние силы, то, в состоянии термодинамического равновесия, газ равномерно распределен по заданному объему. В этом случае давление и плотность газа одинаковы во всех точках. Если же газ находится в силовом поле (как, например, атмосферный воздух, который испытывает притяжение Земли), то давление и плотность газа уже не будут всюду одинаковыми, а будут меняться от точки к точке.
Видео 3.4. Распределение молекул газа по высоте сосуда, находящегося в однородном поле тяжести.
Барометрическая формула. Найдем закон, по которому изменяется давление атмосферы (или плотность воздуха) по мере удаления от поверхности Земли. Выделим вертикальный столб воздуха с площадью горизонтального сечения
S.
Предположим, что
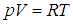
Атмосферное давление на высоте h обусловлено весом вышележащих слоев газа. Пусть на высоте h давление р,тогда на высоте h + dh давление р + dp (рис. 3.6). При этом, если dh > 0, то давление уменьшается, dp < 0, так как уменьшается вес вышележащих слоев атмосферы.
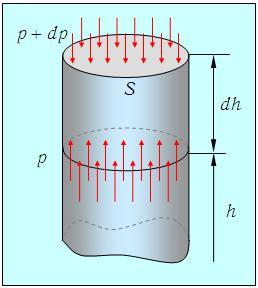
Рис. 3.6.Вертикальный воздушный цилиндр (к выводу барометрической формулы)
Выделенный слой газа, высотой dh и массой m, находится в равновесии. Следовательно, сумма действующих на него сил равна нулю:
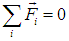
В проекции на вертикальную ось получаем
где r — плотность газа на высоте h. Раскрывая скобки иприводя подобные члены, переходим к уравнению
Воспользуемся уравнением Клапейрона — Менделеева для выделенной массы газа m и выразим плотность через давление:
Подставляя (3.47) в (3.46), окончательно получаем
Это уравнение можно проинтегрировать в случае изотермической атмосферы (Т = const):
Видео 3.5. Барометрическая формула: язычок пламени в роли весьма чувствительного индикатора убывания давления с высотой.
Постоянная интегрирования р0равна давлению на поверхности (h = 0). Полученная зависимость называется барометрической формулой. Она описывает распределение давления газа по высоте в однородном поле тяжести при постоянной температуре. Следует обратить внимание на то, что распределение зависит от рода газа. Чем меньше m, тем меньше по абсолютной величине показатель степени, и тем медленнее для такого газа уменьшается давление при увеличении высоты. На рис. 3.7 показаны зависимости давления от высоты при температуре Т = 300 К (27 °С) для трех газов различной молярной массы — водорода Н2 (m1 = 2,016 г/моль), азота N2 (m2 = 28,013 г/моль) и кислорода 02 (m3 = 31,999 г/моль).
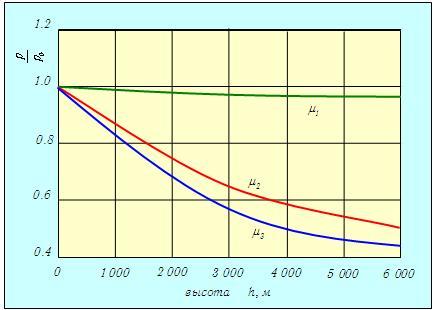
Рис. 3.7. Зависимость давления трех разных газов Н2, N2 и O2 от высоты
Пример. Определим, на какой высоте давление кислорода уменьшается в два раза (при Т = 300 К).
Применяем барометрическую формулу.
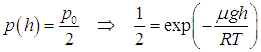
Тогда
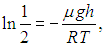
откуда
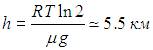
Используя уравнение идеального газа в форме
из барометрической формулы легко получить закон изменения с высотой числа n молекул в единице объема:
Из (3.51) следует, что состав воздуха с ростом высоты будет меняться количественно: возрастет концентрация газов с малой молярной массой, например водорода и гелия.
У поверхности воздух представляет собой смесь газов: N2 — 78,08 %, O2 — 20,95 %, СO2 — 0,03 %, инертные газы — 0,94 %. Посмотрим, как изменится отношение концентраций кислорода и азота в изотермической атмосфере (Т = 300 К) на высоте 10 км.
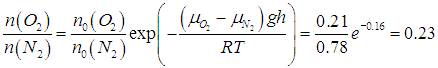
Отношение концентраций кислорода и азота уменьшится от 0,27 до 0,23. Наш расчет справедлив лишь для изотермической атмосферы и сравнительно небольших высот, для которых ускорение свободного падения изменяется незначительно: g = const, T = const.
Распределение Больцмана. Число молекул в единице объема зависит от высоты h и температуры Т, причем обе переменные входят в показатель экспоненты. Уравнение (3.51) можно записать в виде
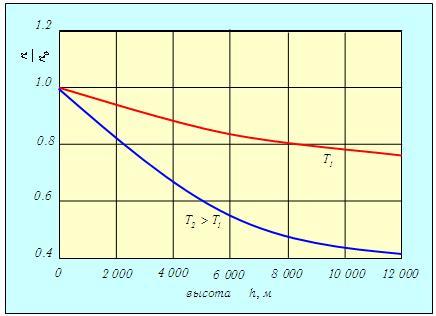
где kB — масса одной молекулы газа. При этом выражение m0gh,стоящее в числителе, есть не что иное, как потенциальная энергия одной молекулы в поле тяжести Земли. Поэтому можно говорить, что мы имеем распределение молекул по значениям потенциальной энергии. При этом чем больше потенциальная энергия, тем меньше таких молекул. В знаменателе показателя степени стоит kBТ — величина, пропорциональная средней энергии теплового движения молекулы. Чем выше температура, то есть чем больше энергия теплового движения молекул, тем экспоненциальный множитель, пропорциональный концентрации молекул, с ростом высоты убывает медленнее. На рис. 3.8 показаны кривые относительной концентрации молекул кислорода O2на разных высотах при двух различных температурах Т1 = 300 К и Т2 = 1 300 К (последний случай, конечно, нереален и используется лишь как иллюстрация).
 ).
).Эксперимент по проверке распределения Максвелла. Необходимо еще раз подчеркнуть, что установленный Максвеллом закон распределения молекул по скоростям и все вытекающие из него следствия справедливы только для газа, находящегося в равновесии.
Закон справедлив для любого числа молекул N, если только это число достаточно велико. Закон Максвелла — статистический, а законы статистики выполняются тем точнее, чем к большему числу одинаковых объектов они применяются. При малом числе объектов могут наблюдаться значительные отклонения от предсказанной статистики — флуктуации.
Экспериментальное определение распределения скоростей молекул было осуществлено впервые О. Штерном в 1920 г. Исследовалось распределение по скоростям одноатомных молекул паров металлов (Ag или Pt), из которых была изготовлена нить, расположенная на оси двух цилиндров. Нить нагревалась электрическим током, и металл испарялся (см. рис 3.5).

Рис. 3.5 Схема опыта Штерна: 1 — вид установки сбоку; 2 — вид установки сверху
Молекулы, прошедшие через щель во внутреннем цилиндре, летели по прямой и оседали на стенке холодного внешнего цилиндра. Если привести всю установку во вращение (щель все время против точки В0), то молекулы, обладающие большой скоростью v, попадут в некоторую точку вблизи В0, а более медленные затратят на путь больше времени и попадут в точки, отстоящие дальше от В0. Следует обратить внимание, что вылетающие молекулы движутся по прямой, они не участвуют во вращательном движении. Поскольку молекулы в зависимости от скорости попадают в разные точки внешнего цилиндра, то исследуя толщину слоя металла, осевшего на его стенку, можно составить представление о распределении молекул по скоростям.
Найдем распределение молекул по расстояниям S от точки В0 до места их попадания на стенку цилиндра. Если R и r —радиусы большого и малого цилиндров, соответственно (см. рис.), то время полета от щели до стенки цилиндра
За это время цилиндр повернется на угол
где ω — угловая скорость вращения установки. Соответственно, точка попадания будет смещена относительно В0 на расстояние
Подставляя сюда время полета, получаем связь скорости молекулы с расстоянием S:
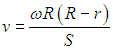
Подставляя, в свою очередь, полученное выражение в распределение Максвелла и учитывая, что
находим распределение молекул по расстояниям S:
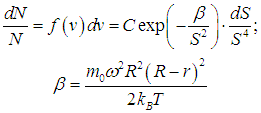
(мы опускаем выражение для нормировочной постоянной С).
Опыты Штерна подтвердили справедливость закона, установленного Максвеллом.
3.4. Распределение молекул по координатам
В этом разделе мы перейдем теперь к анализу распределения молекул газа по координатам. Очевидно, что если на молекулы газа не действуют внешние силы, то, в состоянии термодинамического равновесия, газ равномерно распределен по заданному объему. В этом случае давление и плотность газа одинаковы во всех точках. Если же газ находится в силовом поле (как, например, атмосферный воздух, который испытывает притяжение Земли), то давление и плотность газа уже не будут всюду одинаковыми, а будут меняться от точки к точке.
Видео 3.4. Распределение молекул газа по высоте сосуда, находящегося в однородном поле тяжести.
Барометрическая формула. Найдем закон, по которому изменяется давление атмосферы (или плотность воздуха) по мере удаления от поверхности Земли. Выделим вертикальный столб воздуха с площадью горизонтального сечения
S.
Предположим, что
-
этот столб находится в тепловом равновесии, то есть температура везде одинакова (в реальной атмосфере это не так, но для простоты анализа будем предполагать Т = const); -
газ идеальный, то есть для него справедливо уравнение Клапейрона — Менделеева
-
можно пренебречь изменением ускорения свободного падения g с высотой (что справедливо для не очень больших высот).
Атмосферное давление на высоте h обусловлено весом вышележащих слоев газа. Пусть на высоте h давление р,тогда на высоте h + dh давление р + dp (рис. 3.6). При этом, если dh > 0, то давление уменьшается, dp < 0, так как уменьшается вес вышележащих слоев атмосферы.

Рис. 3.6.Вертикальный воздушный цилиндр (к выводу барометрической формулы)
Выделенный слой газа, высотой dh и массой m, находится в равновесии. Следовательно, сумма действующих на него сил равна нулю:
В проекции на вертикальную ось получаем
| | | (3.45) |
где r — плотность газа на высоте h. Раскрывая скобки иприводя подобные члены, переходим к уравнению
| | | (3.46) |
Воспользуемся уравнением Клапейрона — Менделеева для выделенной массы газа m и выразим плотность через давление:
| | | (3.47) |
Подставляя (3.47) в (3.46), окончательно получаем
| | 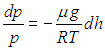 | (3.48) |
Это уравнение можно проинтегрировать в случае изотермической атмосферы (Т = const):
| | 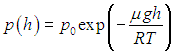 | (3.49) |
Видео 3.5. Барометрическая формула: язычок пламени в роли весьма чувствительного индикатора убывания давления с высотой.
Постоянная интегрирования р0равна давлению на поверхности (h = 0). Полученная зависимость называется барометрической формулой. Она описывает распределение давления газа по высоте в однородном поле тяжести при постоянной температуре. Следует обратить внимание на то, что распределение зависит от рода газа. Чем меньше m, тем меньше по абсолютной величине показатель степени, и тем медленнее для такого газа уменьшается давление при увеличении высоты. На рис. 3.7 показаны зависимости давления от высоты при температуре Т = 300 К (27 °С) для трех газов различной молярной массы — водорода Н2 (m1 = 2,016 г/моль), азота N2 (m2 = 28,013 г/моль) и кислорода 02 (m3 = 31,999 г/моль).

Рис. 3.7. Зависимость давления трех разных газов Н2, N2 и O2 от высоты
Пример. Определим, на какой высоте давление кислорода уменьшается в два раза (при Т = 300 К).
Применяем барометрическую формулу.
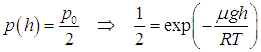
Тогда
откуда
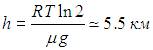
Используя уравнение идеального газа в форме
| | | (3.50) |
из барометрической формулы легко получить закон изменения с высотой числа n молекул в единице объема:
| | 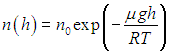 | (3.51) |
Из (3.51) следует, что состав воздуха с ростом высоты будет меняться количественно: возрастет концентрация газов с малой молярной массой, например водорода и гелия.
У поверхности воздух представляет собой смесь газов: N2 — 78,08 %, O2 — 20,95 %, СO2 — 0,03 %, инертные газы — 0,94 %. Посмотрим, как изменится отношение концентраций кислорода и азота в изотермической атмосфере (Т = 300 К) на высоте 10 км.
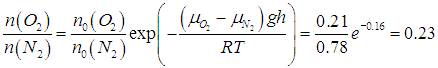
Отношение концентраций кислорода и азота уменьшится от 0,27 до 0,23. Наш расчет справедлив лишь для изотермической атмосферы и сравнительно небольших высот, для которых ускорение свободного падения изменяется незначительно: g = const, T = const.
Распределение Больцмана. Число молекул в единице объема зависит от высоты h и температуры Т, причем обе переменные входят в показатель экспоненты. Уравнение (3.51) можно записать в виде
| | 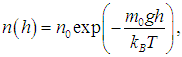 | (3.53) |
где kB — масса одной молекулы газа. При этом выражение m0gh,стоящее в числителе, есть не что иное, как потенциальная энергия одной молекулы в поле тяжести Земли. Поэтому можно говорить, что мы имеем распределение молекул по значениям потенциальной энергии. При этом чем больше потенциальная энергия, тем меньше таких молекул. В знаменателе показателя степени стоит kBТ — величина, пропорциональная средней энергии теплового движения молекулы. Чем выше температура, то есть чем больше энергия теплового движения молекул, тем экспоненциальный множитель, пропорциональный концентрации молекул, с ростом высоты убывает медленнее. На рис. 3.8 показаны кривые относительной концентрации молекул кислорода O2на разных высотах при двух различных температурах Т1 = 300 К и Т2 = 1 300 К (последний случай, конечно, нереален и используется лишь как иллюстрация).
