Файл: Положение о равномерном распределении молекул в пространстве и равномерном распределении их скоростей по всем направлениям называют.docx

Соотношения (3.31), (3.32) могут быть полезны для анализа изменения функции распределения при изменении температуры газа или при изменении рода газа, то есть массы молекул. Отметим, что как следует из (3.26) – (3.29), распределение Максвелла зависит не отдельно от массы молекул и отдельно от температуры газа, а от их отношения  . Поэтому распределение не только «буквенно» но и численно одно и тоже, например, для  молекулярного водорода      при температуре   и для гелия      при температуре  .

 

С ростом температуры наиболее вероятная скорость v_ВЕР (3.31) увеличивается, то есть максимум функции f(v) сдвигается вправо (см. рис. 3.3), Т₂ > Т₁. При этом f(v_ВЕР) уменьшается, то есть кривая становится более пологой. Так же деформируется кривая, если температура постоянна, но масса молекул уменьшается. Напомним, что при любых деформациях функции распределения f(v) площадь под кривыми постоянна и равна единице в соответствии с формулой (3.30 ).

 

Относительное количество молекул, скорость которых превышает некоторое значение v₀, определяется выражением

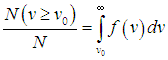(3.33)

На графике (см. рис. 3.3) этому интегралу соответствует лежащая справа от v₀ часть площади (отмечена штриховкой), ограниченная кривой 

---

f(v) и осью скоростей. Как видно из рис. 3.3, относительное количество молекул, имеющих скорости, превышающие v₀, растет с повышением температуры.

 

В заключение этого раздела заметим, что во всех формулах для функции распределения и характерных скоростей входит отношение массы молекулы к постоянной Больцмана



Умножая числитель и знаменатель на число Авогадро N_A и учитывая, что



— молярная масса газа, a



— универсальная газовая постоянная, мы всюду можем использовать это отношение в наиболее удобной для конкретной задачи форме



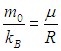
Распределение молекул по величинам безразмерной скорости. Если при графическом изображении функции распределения Максвелла (3.29) по оси абсцисс откладывать скорости молекул v, то форма кривой и положение максимума будут зависеть от массы молекул и от температуры газа. Но если по горизонтальной оси откладывать отношение скорости к наиболее вероятной скорости, то есть безразмерную скорость



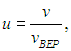
то для всех температур и любых масс молекул (любых газов) получится одна и та же кривая (рис. 3.4).



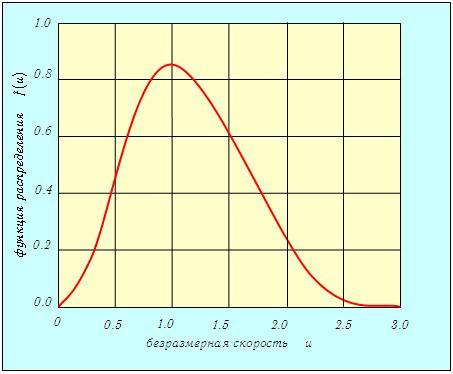
Рис. 3.4.Распределение Максвелла по величинам безразмерной скорости

Сделав замену переменной



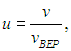
в (3.29 ) и учитывая, что

---

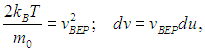
получим распределение Максвелла в форме

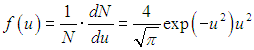(3.34)

Эта формула и соответствующий ей график (см. рис. 3.4) удобны для решения многих задач.

Пример. Найдем, какая часть общего числа молекул кислорода имеет при температуре 27 °С скорости, отличающиеся от наиболее вероятной не более, чем на 1 %; а также скорости в интервале 562–572 м/с.

Произведем необходимые вычисления. Чтобы ответить на первый вопрос задачи, учтем, что u = 1 при v = v_ВЕР. Величина интервала du = 0,02. Следовательно,



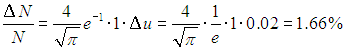
Вычислим наиболее вероятную скорость:



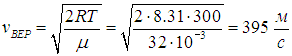
Найдем отношение v = 562 м/с к v_ВЕР = 395 м/с



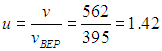
Определим по кривой (см. рис. 3.4) значение функции f(u) при u = 1,42. Получаем f(u) = 0,62. Ширина интервала Dv = 10 м/с(Du = 10/395 = 0,0253). Следовательно, доля молекул в этом интервале



Интересно отметить, что молекула кислорода проходит за секунду путь, равный в среднем 0,4 км. Но не нужно забывать о соударениях молекул. Из-за них молекула по прямой движется очень недолго, и ее путь представляет собой ломаную линию. Поэтому молекула, двигаясь с огромной скоростью по отдельным звеньям ломаной траектории, передвигается от слоя к слою газа со сравнительно небольшой скоростью.

Средняя арифметическая скорость. Знание функции распределения молекул по скоростям f(v) дает возможность найти среднее значение скорости, а также любой величины, являющейся функцией скорости, например квадрата скорости 

---

v² или кинетической энергии молекулы mv²/2.

Средняя арифметическая скорость  — это отношение суммы абсолютных величин скоростей всех молекул в системе к числу этих молекул.

Разобьем интервал всех возможных значений скорости от 0 до бесконечности на малые интервалы Dv_i. Каждому интервалу соответствует количество молекул

(3.35)

Так как интервалы Dv_i, малы, то можно приближенно считать скорости молекул данного интервала одинаковыми и равными v_i. Сумма значений скоростей молекул интервала

(3.36)

Сумма значений скоростей всех молекул

(3.37)

Разделив эту сумму на число молекул, получим выражение для средней арифметической скорости

(3.38)

Переходя от суммы к интегралу, получаем

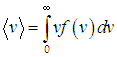(3.39)

Вычисляя интеграл, получаем среднюю арифметическую скорость молекул

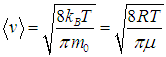(3.40)

---

Среднеквадратичная скорость. Чтобы найти среднее значение произвольной функции L(v) скорости, нужно эту функцию умножить на функцию распределения и проинтегрировать по всем возможным значениям скорости:

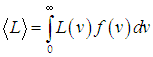(3.41)

В частности, при L(v) = v отсюда находится .

Среднее значение квадрата скорости равно отношению суммы квадратов скоростей всех молекул системы к общему числу молекул. Таким образом,

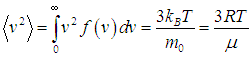(3.41)

Среднеквадратичная скорость — это корень квадратный из среднего значения квадрата скорости молекул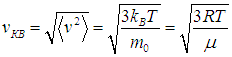

Следует отметить, что характерные скорости отличаются друг от друга лишь численными множителями, причем

(3.43)

а зависимость от Т и m₀ (или m) у них одинаковая.

Через среднеквадратичную скорость выражается средняя кинетическая энергия поступательного движения молекул

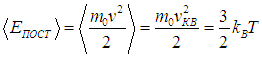(3.44)

Этот результат находится в согласии с формулой (1.14) кинетической теории идеальных газов и с законом о равнораспределении энергии, который гласит, что на каждую степень свободы молекулы приходится энергия 

---