Файл: Учебнометодическое пособие по дисциплине физика часть 1 Физические основы механики. Электричество. Электромагнетизм. Для студентов 1 курса.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.12.2023
Просмотров: 535
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Дж.
При определении теплоты пределы интегрирования
пределы интегрирования 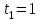 с,
с, 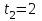 с и
с и
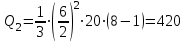 Дж.
Дж.
Следовательно,
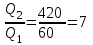 ,
,
т. е. за вторую секунду выделится теплоты в 7 раз больше, чем за первую.
П р и м е р 11 . Электрон , влетевший в однородное магнитное поле под некоторым углом к линиям индукции
к линиям индукции 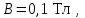 движется по винтовой линии с радиусом R=0,2 мм и шагом h =1,4 мм. Определить скорость электрона .
движется по винтовой линии с радиусом R=0,2 мм и шагом h =1,4 мм. Определить скорость электрона .
Дано: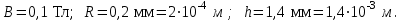
Найти :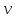
Р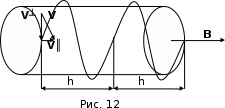 е ш е н и е. На движущийся в магнитном поле электрон (рис. 12) действует сила Лоренца, перпендикулярная векторам магнитной индукции
е ш е н и е. На движущийся в магнитном поле электрон (рис. 12) действует сила Лоренца, перпендикулярная векторам магнитной индукции 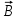 и скорости электрона
и скорости электрона 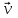 .
.
Абсолютная величина силы Лоренца выражается формулой
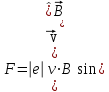
Известно, что постоянная сила, перпендикулярная скорости, вызывает движение по окружности. Следовательно, электрон, влетевший в магнитное поле, будет двигаться по окружности в плоскости, перпендикулярной вектору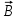 , со скоростью
, со скоростью 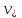 .
.
Одновременно он будет двигаться и вдоль поля со скоростью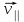 :
:
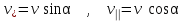
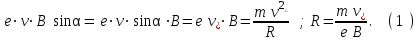
Шаг винтовой линии, т.е. путь, проходимый электроном вдоль поля за время одного оборота,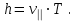
Поскольку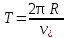 , для шага получаем выражение
, для шага получаем выражение
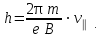 (2)
(2)
Выразим составляющие скорости электрона из (1) и (2):
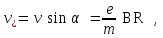
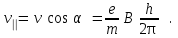
Исключая угол , находим
, находим :
:
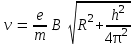
Проверим размерность результата:
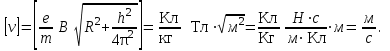
Рассчитаем результат:
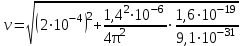

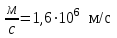 ‒
‒
П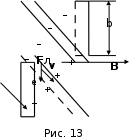 р и м е р 12. При наблюдении эффекта Холла в пластине с шириной
р и м е р 12. При наблюдении эффекта Холла в пластине с шириной 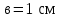 (рис. 13) холловская разность потенциалов составила
(рис. 13) холловская разность потенциалов составила 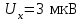 .Определить скорость упорядоченного движения носителей тока
.Определить скорость упорядоченного движения носителей тока  , если магнитная индукция
, если магнитная индукция 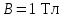 .
.
Дано:
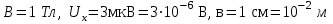
Найти:
Р
j =nev
е ш е н и е . Получим выражение для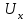 . Пусть ток течет по пластине, помещенной в магнитное поле, перпендикулярное ее широким граням. На носители тока, имеющие скорость упорядоченного движения
. Пусть ток течет по пластине, помещенной в магнитное поле, перпендикулярное ее широким граням. На носители тока, имеющие скорость упорядоченного движения  , действует сила Лоренца
, действует сила Лоренца
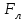 :
:

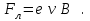
Сила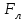 перпендикулярна
перпендикулярна  , она отклоняет носители к ”горизонтальным” (см. рис. 13) граням, вызывая перераспределение зарядов и, следовательно, дополнительное поперечное электрическое поле
, она отклоняет носители к ”горизонтальным” (см. рис. 13) граням, вызывая перераспределение зарядов и, следовательно, дополнительное поперечное электрическое поле 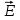 и связанную с ним холловскую разность потенциалов
и связанную с ним холловскую разность потенциалов  . Величину последней найдем из условия стационарности возникшего электрического поля,выражаемого равенством силы Лоренца силе, действующей со стороны этого поля :
. Величину последней найдем из условия стационарности возникшего электрического поля,выражаемого равенством силы Лоренца силе, действующей со стороны этого поля :
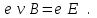 (1)
(1)
Поскольку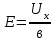 получим
получим
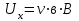 . (2)
. (2)
Скорость можно выразить из формулы для плотности тока
можно выразить из формулы для плотности тока 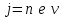 , где n – концентрация носителей тока:
, где n – концентрация носителей тока:
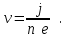 (3)
(3)
С учетом этого имеем
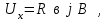 (4)
(4)
где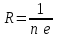 -постоянная Холла.
-постоянная Холла.
Ответ на вопрос задачи получим из формулы(2):
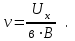
Проверим размерность результата:
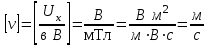
Р ассчитаем результат:
ассчитаем результат:
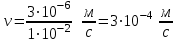
П
a
р и м е р 13. Плоский квадратный контур со стороной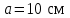 , по которому течет ток
, по которому течет ток 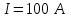 , свободно установился в однородном магнитном поле с индукцией B=1Тл (рис. 14). Определить работу
, свободно установился в однородном магнитном поле с индукцией B=1Тл (рис. 14). Определить работу  , совершаемую внешними силами при повороте контура относительно оси, проходящей через середину его противоположных сторон, на угол: 1)
, совершаемую внешними силами при повороте контура относительно оси, проходящей через середину его противоположных сторон, на угол: 1)
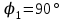 ; 2)
; 2)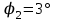 . При повороте контура сила тока в нем поддерживается неизменной.
. При повороте контура сила тока в нем поддерживается неизменной.
Дано: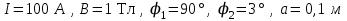

Найти: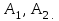
Р е ш е н и е . Как известно, на контур с током в магнитном поле действует момент сил
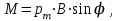 (1)
(1)
где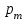 -магнитный момент контура,
-магнитный момент контура, 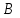 –магнитная индукция;
–магнитная индукция;  - угол между вектором
- угол между вектором 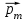 , направленным по нормали к контуру, и вектором
, направленным по нормали к контуру, и вектором 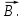
По условию задачи, в начальном положении контур свободно установился в магнитном поле. При этом момент сил равен нулю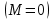 , а значит,
, а значит, 
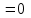 ,т.е. вектора
,т.е. вектора 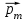 и
и  совпадают по направлению.
совпадают по направлению.
Если внешние силы выведут контур из положения равновесия, то возникающий момент сил, определяемый формой (1), будет стремиться возвратить контур в исходное положение. Против этого момента и будет совершаться работа внешними силами. Так как момент сил переменный (зависит от угла поворота ), то для подсчета работы применим формулу работы в дифференциальной форме
), то для подсчета работы применим формулу работы в дифференциальной форме
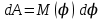
Подставив сюда выражение М по формуле (1) и учтя, что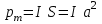 ,
,
где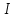 - сила тока в контуре,
- сила тока в контуре,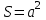 - площадь контура, получим
- площадь контура, получим
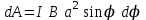 (2)
(2)
1. Работа при повороте на угол :
:
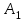 =
=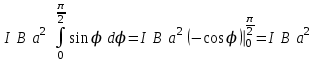 (3)
(3)
2. Работа при повороте на угол . В этом случае, учитывая малость угла
. В этом случае, учитывая малость угла 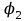 , заменим в выражении (2)
, заменим в выражении (2) 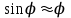 :
:
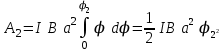
Здесь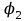 следует выразить в радианах .
следует выразить в радианах .
Рассчитаем результат:
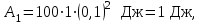
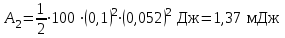 .
.
Отметим, что задача могла быть решена и другим способом. Известно, что работа внешних сил по перемещению контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока через контур
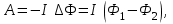
где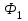 -магнитный поток , пронизывающий контур до перемещения ;
-магнитный поток , пронизывающий контур до перемещения ;
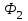 -то же после перемещения .
-то же после перемещения .
П
B
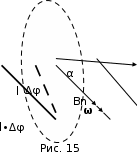 р и м е р 14. В однородном магнитном поле (B= 0,2 мТл) равномерно вращается с частотой
р и м е р 14. В однородном магнитном поле (B= 0,2 мТл) равномерно вращается с частотой 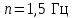 проводник длиной
проводник длиной 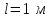 , с током
, с током 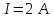 . Ось вращения проходит через один из концов проводника и составляет угол
. Ось вращения проходит через один из концов проводника и составляет угол 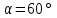 cвектором
cвектором  (рис.15). Определить мощность
(рис.15). Определить мощность 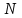 , затрачиваемую на вращение проводника.
, затрачиваемую на вращение проводника.
Дано: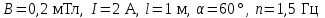 .
.
Определить :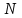 .
.
Р е ш е н и е . Работа перемещения проводника с током в магнитном поле равна произведению силы тока на изменение потока индукции магнитного поля через площадь поверхности, которую описывает проводник при своем движении :
При определении теплоты
 пределы интегрирования
пределы интегрирования 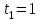 с,
с, 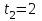 с и
с и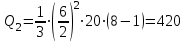 Дж.
Дж.Следовательно,
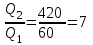 ,
,т. е. за вторую секунду выделится теплоты в 7 раз больше, чем за первую.
П р и м е р 11 . Электрон , влетевший в однородное магнитное поле под некоторым углом
 к линиям индукции
к линиям индукции 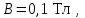 движется по винтовой линии с радиусом R=0,2 мм и шагом h =1,4 мм. Определить скорость электрона .
движется по винтовой линии с радиусом R=0,2 мм и шагом h =1,4 мм. Определить скорость электрона .Дано:
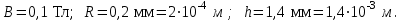
Найти :
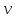
Р
 е ш е н и е. На движущийся в магнитном поле электрон (рис. 12) действует сила Лоренца, перпендикулярная векторам магнитной индукции
е ш е н и е. На движущийся в магнитном поле электрон (рис. 12) действует сила Лоренца, перпендикулярная векторам магнитной индукции 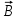 и скорости электрона
и скорости электрона 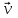 .
. Абсолютная величина силы Лоренца выражается формулой
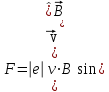
Известно, что постоянная сила, перпендикулярная скорости, вызывает движение по окружности. Следовательно, электрон, влетевший в магнитное поле, будет двигаться по окружности в плоскости, перпендикулярной вектору
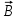 , со скоростью
, со скоростью 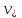 .
.Одновременно он будет двигаться и вдоль поля со скоростью
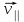 :
: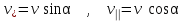
В результате происходит движение электрона по винтовой линии
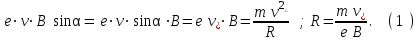
Шаг винтовой линии, т.е. путь, проходимый электроном вдоль поля за время одного оборота,
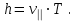
Поскольку
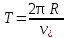 , для шага получаем выражение
, для шага получаем выражение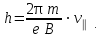 (2)
(2)Выразим составляющие скорости электрона из (1) и (2):
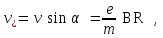
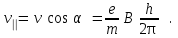
Исключая угол
 , находим
, находим :
: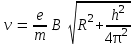
Проверим размерность результата:
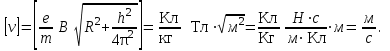
Рассчитаем результат:
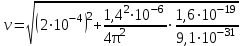

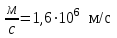 ‒
‒П
 р и м е р 12. При наблюдении эффекта Холла в пластине с шириной
р и м е р 12. При наблюдении эффекта Холла в пластине с шириной 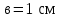 (рис. 13) холловская разность потенциалов составила
(рис. 13) холловская разность потенциалов составила 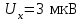 .Определить скорость упорядоченного движения носителей тока
.Определить скорость упорядоченного движения носителей тока  , если магнитная индукция
, если магнитная индукция 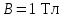 .
. Дано:
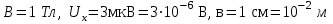
Найти:

Р
j =nev
е ш е н и е . Получим выражение для
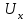 . Пусть ток течет по пластине, помещенной в магнитное поле, перпендикулярное ее широким граням. На носители тока, имеющие скорость упорядоченного движения
. Пусть ток течет по пластине, помещенной в магнитное поле, перпендикулярное ее широким граням. На носители тока, имеющие скорость упорядоченного движения  , действует сила Лоренца
, действует сила Лоренца
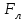 :
:
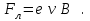
Сила
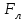 перпендикулярна
перпендикулярна  , она отклоняет носители к ”горизонтальным” (см. рис. 13) граням, вызывая перераспределение зарядов и, следовательно, дополнительное поперечное электрическое поле
, она отклоняет носители к ”горизонтальным” (см. рис. 13) граням, вызывая перераспределение зарядов и, следовательно, дополнительное поперечное электрическое поле 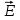 и связанную с ним холловскую разность потенциалов
и связанную с ним холловскую разность потенциалов  . Величину последней найдем из условия стационарности возникшего электрического поля,выражаемого равенством силы Лоренца силе, действующей со стороны этого поля :
. Величину последней найдем из условия стационарности возникшего электрического поля,выражаемого равенством силы Лоренца силе, действующей со стороны этого поля :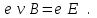 (1)
(1)Поскольку
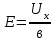 получим
получим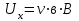 . (2)
. (2)Скорость
 можно выразить из формулы для плотности тока
можно выразить из формулы для плотности тока 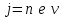 , где n – концентрация носителей тока:
, где n – концентрация носителей тока: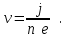 (3)
(3)С учетом этого имеем
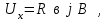 (4)
(4)где
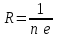 -постоянная Холла.
-постоянная Холла.Ответ на вопрос задачи получим из формулы(2):
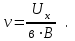
Проверим размерность результата:
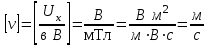
Р
 ассчитаем результат:
ассчитаем результат: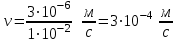
П
a
р и м е р 13. Плоский квадратный контур со стороной
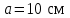 , по которому течет ток
, по которому течет ток 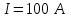 , свободно установился в однородном магнитном поле с индукцией B=1Тл (рис. 14). Определить работу
, свободно установился в однородном магнитном поле с индукцией B=1Тл (рис. 14). Определить работу  , совершаемую внешними силами при повороте контура относительно оси, проходящей через середину его противоположных сторон, на угол: 1)
, совершаемую внешними силами при повороте контура относительно оси, проходящей через середину его противоположных сторон, на угол: 1)
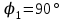 ; 2)
; 2)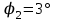 . При повороте контура сила тока в нем поддерживается неизменной.
. При повороте контура сила тока в нем поддерживается неизменной. Дано:
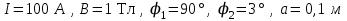

Найти:
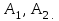
Р е ш е н и е . Как известно, на контур с током в магнитном поле действует момент сил
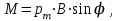 (1)
(1)где
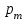 -магнитный момент контура,
-магнитный момент контура, 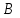 –магнитная индукция;
–магнитная индукция;  - угол между вектором
- угол между вектором 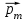 , направленным по нормали к контуру, и вектором
, направленным по нормали к контуру, и вектором 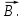
По условию задачи, в начальном положении контур свободно установился в магнитном поле. При этом момент сил равен нулю
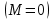 , а значит,
, а значит, 
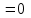 ,т.е. вектора
,т.е. вектора 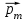 и
и  совпадают по направлению.
совпадают по направлению.Если внешние силы выведут контур из положения равновесия, то возникающий момент сил, определяемый формой (1), будет стремиться возвратить контур в исходное положение. Против этого момента и будет совершаться работа внешними силами. Так как момент сил переменный (зависит от угла поворота
 ), то для подсчета работы применим формулу работы в дифференциальной форме
), то для подсчета работы применим формулу работы в дифференциальной форме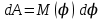
Подставив сюда выражение М по формуле (1) и учтя, что
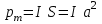 ,
,где
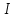 - сила тока в контуре,
- сила тока в контуре,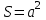 - площадь контура, получим
- площадь контура, получим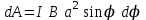 (2)
(2)1. Работа при повороте на угол
 :
: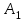 =
=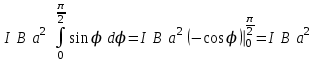 (3)
(3)2. Работа при повороте на угол
 . В этом случае, учитывая малость угла
. В этом случае, учитывая малость угла 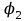 , заменим в выражении (2)
, заменим в выражении (2) 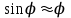 :
: 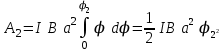
Здесь
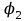 следует выразить в радианах .
следует выразить в радианах .Рассчитаем результат:
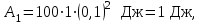
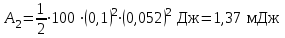 .
.Отметим, что задача могла быть решена и другим способом. Известно, что работа внешних сил по перемещению контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока через контур
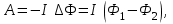
где
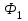 -магнитный поток , пронизывающий контур до перемещения ;
-магнитный поток , пронизывающий контур до перемещения ;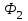 -то же после перемещения .
-то же после перемещения .П
B
 р и м е р 14. В однородном магнитном поле (B= 0,2 мТл) равномерно вращается с частотой
р и м е р 14. В однородном магнитном поле (B= 0,2 мТл) равномерно вращается с частотой 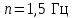 проводник длиной
проводник длиной 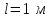 , с током
, с током 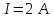 . Ось вращения проходит через один из концов проводника и составляет угол
. Ось вращения проходит через один из концов проводника и составляет угол 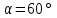 cвектором
cвектором  (рис.15). Определить мощность
(рис.15). Определить мощность 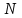 , затрачиваемую на вращение проводника.
, затрачиваемую на вращение проводника.Дано:
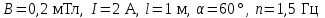 .
.Определить :
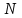 .
.Р е ш е н и е . Работа перемещения проводника с током в магнитном поле равна произведению силы тока на изменение потока индукции магнитного поля через площадь поверхности, которую описывает проводник при своем движении :