Файл: Учебнометодическое пособие по дисциплине физика часть 1 Физические основы механики. Электричество. Электромагнетизм. Для студентов 1 курса.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.12.2023
Просмотров: 530
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(4)
Из формулы (4) видно, что наименование результата получится в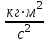 , т.е. в джоулях.
, т.е. в джоулях.
Подставляя числовые значения в (4), получим
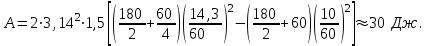
П р и м е р 9. Сколько времени будет скатываться без скольжения обруч с наклонной плоскости длиной
будет скатываться без скольжения обруч с наклонной плоскости длиной 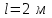 и высотой
и высотой 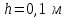 ? Начальная скорость
? Начальная скорость
о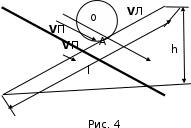 бруча
бруча  .
.
Дано: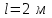 ;
; 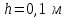 .
.
Найти: .
.
Р е ш е н и е .Движение обруча вдоль наклонной плоскости можно считать равноускоренным, так как равнодействующая всех внешних сил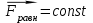 .
.
При равноускоренном движении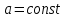 , а
, а 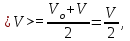 так как
так как 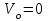
Пройденный путь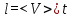 , откуда искомое время
, откуда искомое время
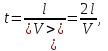 (1)
(1)
Чтобы найти , необходимо рассчитать конечную скорость
, необходимо рассчитать конечную скорость  обруча у основания наклонной плоскости (рис. 4). Скатывание происходит без скольжения, поэтому малыми силами трения качения мы можем пренебречь. Кроме того, так как нет скольжения, то
обруча у основания наклонной плоскости (рис. 4). Скатывание происходит без скольжения, поэтому малыми силами трения качения мы можем пренебречь. Кроме того, так как нет скольжения, то
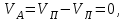 (2)
(2)
где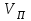 - скорость поступательного движения обруча,
- скорость поступательного движения обруча, 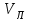 - линейная скорость движения точки касания А обруча с плоскостью.
- линейная скорость движения точки касания А обруча с плоскостью.
Из уравнения (2) получим, что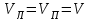 .
.
При качении полная кинетическая энергия складывается из кинетической энергии
поступательного и вращательного движения
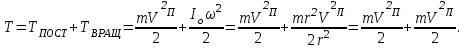
Так как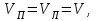 то
то 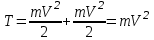
В системе действуют только консервативные силы тяжести, поэтому полный запас механической энергии не меняется, а возрастание кинетической энергии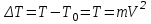 численно равно убыванию потенциальной
численно равно убыванию потенциальной 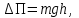 т.е.
т.е. 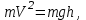 откуда
откуда 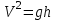 . (3)
. (3)
Подставляя (3) в (1) , имеем
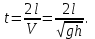 (4)
(4)
Проверим размерность результата:
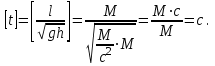
Рассчитаем значение ,подставив в данное значение и
и 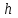 :
:
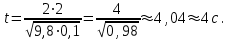
ЭЛЕКТРОСТАТИКА, ПОСТОЯННЫЙ ТОК И ЭЛЕКТРОМАГНЕТИЗМ
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
П р и м е р 1. Тонкий стержень длиной l = 20 см несет равномерно распределенный заряд. На продолжении оси стержня на расстоянии а = 10 см от ближайшего конца находится точечный заряд Q1 = 40 нКл, который взаимодействует со стержнем с силой F = 6 мкН. Определить линейную плотность заряда на стержне.
Дано: l = 0,2 м; а = 0,1 м;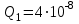 Кл; F = 6∙10-6Н
Кл; F = 6∙10-6Н
Найти: .
Р
F
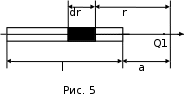 е ш е н и е. Сила взаимодействия F заряженного стержня с точечным зарядом Q1 зависит от линейной плотности заряда на стержне. Зная эту зависимость, можно определить . При вычислении силы F следует иметь в виду, что заряд на стержне не является точечным, поэтому закон Кулона непосредственно применить нельзя. В этом случае можно поступить следующим образом. Выделить на стержне (рис. 5) дифференциально малый участок dr с зарядом
е ш е н и е. Сила взаимодействия F заряженного стержня с точечным зарядом Q1 зависит от линейной плотности заряда на стержне. Зная эту зависимость, можно определить . При вычислении силы F следует иметь в виду, что заряд на стержне не является точечным, поэтому закон Кулона непосредственно применить нельзя. В этом случае можно поступить следующим образом. Выделить на стержне (рис. 5) дифференциально малый участок dr с зарядом 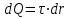 . Этот заряд можно рассматривать как точечный. Тогда согласно закону Кулона
. Этот заряд можно рассматривать как точечный. Тогда согласно закону Кулона
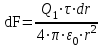 .
.
Интегрируя это выражение в пределах от а до а + l, получим
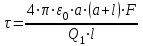 .
.
Проверим правильность наименования результата:
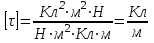 .
.
Учитывая, что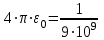 Ф/м, подставим числовые значения в полученную формулу и произведем вычисления:
Ф/м, подставим числовые значения в полученную формулу и произведем вычисления:
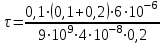 Кл/м =
Кл/м = 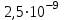 Кл/м = 2,5 нКл/м.
Кл/м = 2,5 нКл/м.
П р и м е р 2. Два точечных электрических заряда Q1 = 1 нКл и Q2 = -2 нКл находятся в воздухе на расстоянии d = 10 см друг от друга. Найти напряженность E и потенциал поля, создаваемого этими зарядами в точке А, удаленной от заряда Q1 на расстояние r1 = 9 см и от заряда Q2 на r2 = 7 см.
р и м е р 2. Два точечных электрических заряда Q1 = 1 нКл и Q2 = -2 нКл находятся в воздухе на расстоянии d = 10 см друг от друга. Найти напряженность E и потенциал поля, создаваемого этими зарядами в точке А, удаленной от заряда Q1 на расстояние r1 = 9 см и от заряда Q2 на r2 = 7 см.
Дано: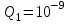 Кл;
Кл; 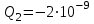 Кл; d = 0,1 м; r1= 0,09 м; r2= 0,07 м.
Кл; d = 0,1 м; r1= 0,09 м; r2= 0,07 м.
Найти: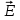 и .
и .
Р е ш е н и е. Согласно принципу суперпозиции электрических полей,
каждый заряд создает поле независимо от присутствия в пространстве других зарядов. Поэтому напряженность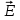 электрического поля в искомой точке может быть найдена как геометрическая сумма напряженностей
электрического поля в искомой точке может быть найдена как геометрическая сумма напряженностей 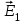 и
и 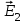 полей, создаваемых каждым зарядом в отдельности
полей, создаваемых каждым зарядом в отдельности
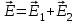 .
.
Напряженность электрического поля, создаваемого в воздухе (=1) первым зарядом,
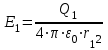 , (1)
, (1)
Вторым зарядом –
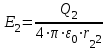 , (2)
, (2)
Вектор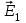

(рис.6) направлен по силовой линии от заряда Q1, так как заряд Q1 положителен; вектор направлен также по силовой линии, но к заряду Q2, так как заряд Q2 отрицателен.
направлен также по силовой линии, но к заряду Q2, так как заряд Q2 отрицателен.
Абсолютное значение вектора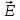 найдем по теореме косинусов:
найдем по теореме косинусов:
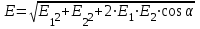 , (3)
, (3)
где - угол между векторами и
и  , который может быть найден из треугольника со сторонами
, который может быть найден из треугольника со сторонами 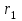 ,
, 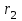 и d:
и d:
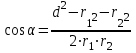 .
.
В данном случае во избежание громоздких записей удобно значение cos вычислить отдельно:
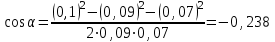 .
.
Подставляя выражение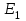 из формулы (1) и
из формулы (1) и 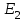 из формулы (2) в равенство (3) и вынося общий множитель
из формулы (2) в равенство (3) и вынося общий множитель 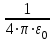 за знак корня, получим
за знак корня, получим
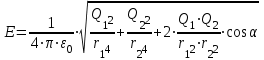 . (4)
. (4)
Проверим правильность наименования результата:
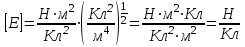 или
или 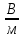 .
.
Подставим числовые значения величин в формулу (4) и произведем вычисления
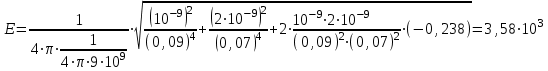 В/м =3,58 кВ/м.
В/м =3,58 кВ/м.
При вычислении Е знак заряда Q2 опущен, так как знак заряда определяет направление вектора напряженности, а направление Е2 было учтено при его графическом изображении.
В соответствии с принципом суперпозиции электрических полей потенциал результирующего поля, созданного двумя зарядами Q1 и Q2, равен алгебраической сумме потенциалов, т. е.
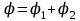 . (5)
. (5)
Потенциал электрического поля, создаваемого в вакууме точечным зарядом Q на расстоянии r от него, выражается формулой
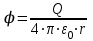 . (6)
. (6)
В нашем случае согласно формулам (5) и (6) получим:
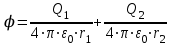
или
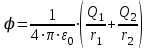 .
.
Подставив в это выражение числовые значения физических величин, получим
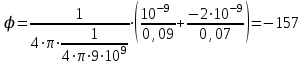 В.
В.
П р и м е р 3. Точечный заряд Q = 25 нКл находится в поле, созданном прямым бесконечным цилиндром радиусом R = 1 см, равномерно заряженным с поверхностной плотностью = 0,2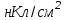 . Определить силу F, действующую на заряд, если его расстояние от оси цилиндра равно 10 см.
. Определить силу F, действующую на заряд, если его расстояние от оси цилиндра равно 10 см.
Дано: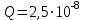 Кл;
Кл; 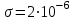
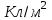 ;
; 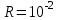 м;
м; 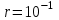 м.
м.
Найти: F.
Р е ш е н и е . Численное значение силы F, действующей на точечный заряд Q, находящийся в электрическом поле, определяется по формуле
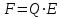 , (1)
, (1)
где Е- напряженность поля.
Как следует из теоремы Гаусса, напряженность поля бесконечно длинного равномерно заряженного цилиндра
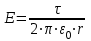 , (2)
, (2)
где - линейная плотность заряда.
Выразим линейную плотность заряда через поверхностную плотность . Для этого выделим элемент цилиндра длиной l и выразим находящийся на нем заряд Q двумя способами:
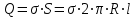 ;
; 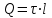 .
.
Приравняв правые части этих равенств, получим
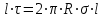 .
.
После сокращения на l найдем
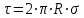 .
.
С учетом этого формула (2) примет вид
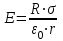 .
.
Подставив это выражение в (1), получим искомую силу
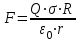 . (3)
. (3)
Учтем, что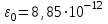 Ф/м, и подставим в (3) числовые значения величин:
Ф/м, и подставим в (3) числовые значения величин:
Из формулы (4) видно, что наименование результата получится в
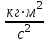 , т.е. в джоулях.
, т.е. в джоулях.Подставляя числовые значения в (4), получим
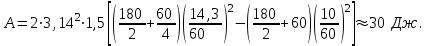
П р и м е р 9. Сколько времени
 будет скатываться без скольжения обруч с наклонной плоскости длиной
будет скатываться без скольжения обруч с наклонной плоскости длиной 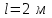 и высотой
и высотой 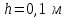 ? Начальная скорость
? Начальная скорость о
 бруча
бруча  .
.Дано:
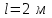 ;
; 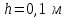 .
.Найти:
 .
.Р е ш е н и е .Движение обруча вдоль наклонной плоскости можно считать равноускоренным, так как равнодействующая всех внешних сил
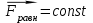 .
.При равноускоренном движении
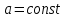 , а
, а 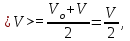 так как
так как 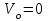
Пройденный путь
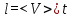 , откуда искомое время
, откуда искомое время 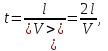 (1)
(1)Чтобы найти
 , необходимо рассчитать конечную скорость
, необходимо рассчитать конечную скорость  обруча у основания наклонной плоскости (рис. 4). Скатывание происходит без скольжения, поэтому малыми силами трения качения мы можем пренебречь. Кроме того, так как нет скольжения, то
обруча у основания наклонной плоскости (рис. 4). Скатывание происходит без скольжения, поэтому малыми силами трения качения мы можем пренебречь. Кроме того, так как нет скольжения, то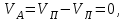 (2)
(2)где
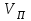 - скорость поступательного движения обруча,
- скорость поступательного движения обруча, 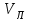 - линейная скорость движения точки касания А обруча с плоскостью.
- линейная скорость движения точки касания А обруча с плоскостью. Из уравнения (2) получим, что
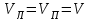 .
.При качении полная кинетическая энергия складывается из кинетической энергии
поступательного и вращательного движения
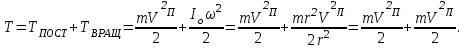
Так как
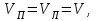 то
то 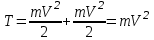
В системе действуют только консервативные силы тяжести, поэтому полный запас механической энергии не меняется, а возрастание кинетической энергии
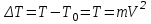 численно равно убыванию потенциальной
численно равно убыванию потенциальной 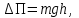 т.е.
т.е. 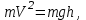 откуда
откуда 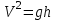 . (3)
. (3)Подставляя (3) в (1) , имеем
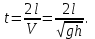 (4)
(4)Проверим размерность результата:
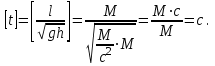
Рассчитаем значение ,подставив в данное значение
 и
и 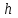 :
: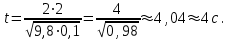
ЭЛЕКТРОСТАТИКА, ПОСТОЯННЫЙ ТОК И ЭЛЕКТРОМАГНЕТИЗМ
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
П р и м е р 1. Тонкий стержень длиной l = 20 см несет равномерно распределенный заряд. На продолжении оси стержня на расстоянии а = 10 см от ближайшего конца находится точечный заряд Q1 = 40 нКл, который взаимодействует со стержнем с силой F = 6 мкН. Определить линейную плотность заряда на стержне.
Дано: l = 0,2 м; а = 0,1 м;
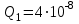 Кл; F = 6∙10-6Н
Кл; F = 6∙10-6НН
Р
F
 е ш е н и е. Сила взаимодействия F заряженного стержня с точечным зарядом Q1 зависит от линейной плотности заряда на стержне. Зная эту зависимость, можно определить . При вычислении силы F следует иметь в виду, что заряд на стержне не является точечным, поэтому закон Кулона непосредственно применить нельзя. В этом случае можно поступить следующим образом. Выделить на стержне (рис. 5) дифференциально малый участок dr с зарядом
е ш е н и е. Сила взаимодействия F заряженного стержня с точечным зарядом Q1 зависит от линейной плотности заряда на стержне. Зная эту зависимость, можно определить . При вычислении силы F следует иметь в виду, что заряд на стержне не является точечным, поэтому закон Кулона непосредственно применить нельзя. В этом случае можно поступить следующим образом. Выделить на стержне (рис. 5) дифференциально малый участок dr с зарядом 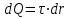 . Этот заряд можно рассматривать как точечный. Тогда согласно закону Кулона
. Этот заряд можно рассматривать как точечный. Тогда согласно закону Кулона 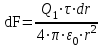 .
. Интегрируя это выражение в пределах от а до а + l, получим 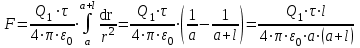 ,
,
откуда интересующая нас линейная плотность заряда
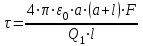 .
.Проверим правильность наименования результата:
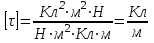 .
.Учитывая, что
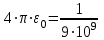 Ф/м, подставим числовые значения в полученную формулу и произведем вычисления:
Ф/м, подставим числовые значения в полученную формулу и произведем вычисления: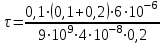 Кл/м =
Кл/м = 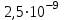 Кл/м = 2,5 нКл/м.
Кл/м = 2,5 нКл/м.
П
 р и м е р 2. Два точечных электрических заряда Q1 = 1 нКл и Q2 = -2 нКл находятся в воздухе на расстоянии d = 10 см друг от друга. Найти напряженность E и потенциал поля, создаваемого этими зарядами в точке А, удаленной от заряда Q1 на расстояние r1 = 9 см и от заряда Q2 на r2 = 7 см.
р и м е р 2. Два точечных электрических заряда Q1 = 1 нКл и Q2 = -2 нКл находятся в воздухе на расстоянии d = 10 см друг от друга. Найти напряженность E и потенциал поля, создаваемого этими зарядами в точке А, удаленной от заряда Q1 на расстояние r1 = 9 см и от заряда Q2 на r2 = 7 см.Дано:
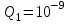 Кл;
Кл; 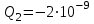 Кл; d = 0,1 м; r1= 0,09 м; r2= 0,07 м.
Кл; d = 0,1 м; r1= 0,09 м; r2= 0,07 м.Найти:
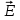 и .
и .Р е ш е н и е. Согласно принципу суперпозиции электрических полей,
каждый заряд создает поле независимо от присутствия в пространстве других зарядов. Поэтому напряженность
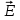 электрического поля в искомой точке может быть найдена как геометрическая сумма напряженностей
электрического поля в искомой точке может быть найдена как геометрическая сумма напряженностей 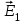 и
и 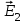 полей, создаваемых каждым зарядом в отдельности
полей, создаваемых каждым зарядом в отдельности 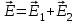 .
.Напряженность электрического поля, создаваемого в воздухе (=1) первым зарядом,
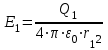 , (1)
, (1)Вторым зарядом –
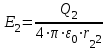 , (2)
, (2)Вектор
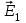

(рис.6) направлен по силовой линии от заряда Q1, так как заряд Q1 положителен; вектор
 направлен также по силовой линии, но к заряду Q2, так как заряд Q2 отрицателен.
направлен также по силовой линии, но к заряду Q2, так как заряд Q2 отрицателен.Абсолютное значение вектора
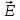 найдем по теореме косинусов:
найдем по теореме косинусов: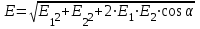 , (3)
, (3)где - угол между векторами
 и
и  , который может быть найден из треугольника со сторонами
, который может быть найден из треугольника со сторонами 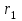 ,
, 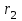 и d:
и d: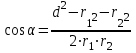 .
.В данном случае во избежание громоздких записей удобно значение cos вычислить отдельно:
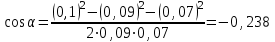 .
.Подставляя выражение
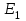 из формулы (1) и
из формулы (1) и 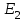 из формулы (2) в равенство (3) и вынося общий множитель
из формулы (2) в равенство (3) и вынося общий множитель 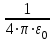 за знак корня, получим
за знак корня, получим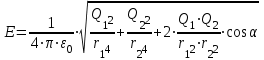 . (4)
. (4)Проверим правильность наименования результата:
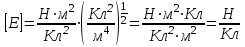 или
или 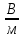 .
.Подставим числовые значения величин в формулу (4) и произведем вычисления
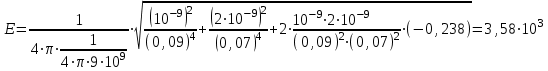 В/м =3,58 кВ/м.
В/м =3,58 кВ/м.При вычислении Е знак заряда Q2 опущен, так как знак заряда определяет направление вектора напряженности, а направление Е2 было учтено при его графическом изображении.
В соответствии с принципом суперпозиции электрических полей потенциал результирующего поля, созданного двумя зарядами Q1 и Q2, равен алгебраической сумме потенциалов, т. е.
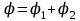 . (5)
. (5)Потенциал электрического поля, создаваемого в вакууме точечным зарядом Q на расстоянии r от него, выражается формулой
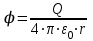 . (6)
. (6)В нашем случае согласно формулам (5) и (6) получим:
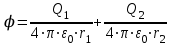
или
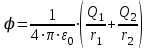 .
.Подставив в это выражение числовые значения физических величин, получим
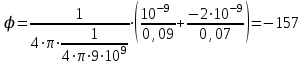 В.
В.П р и м е р 3. Точечный заряд Q = 25 нКл находится в поле, созданном прямым бесконечным цилиндром радиусом R = 1 см, равномерно заряженным с поверхностной плотностью = 0,2
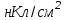 . Определить силу F, действующую на заряд, если его расстояние от оси цилиндра равно 10 см.
. Определить силу F, действующую на заряд, если его расстояние от оси цилиндра равно 10 см.Дано:
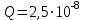 Кл;
Кл; 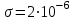
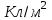 ;
; 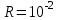 м;
м; 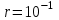 м.
м.Найти: F.
Р е ш е н и е . Численное значение силы F, действующей на точечный заряд Q, находящийся в электрическом поле, определяется по формуле
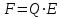 , (1)
, (1)где Е- напряженность поля.
Как следует из теоремы Гаусса, напряженность поля бесконечно длинного равномерно заряженного цилиндра
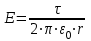 , (2)
, (2)где - линейная плотность заряда.
Выразим линейную плотность заряда через поверхностную плотность . Для этого выделим элемент цилиндра длиной l и выразим находящийся на нем заряд Q двумя способами:
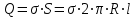 ;
; 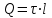 .
.Приравняв правые части этих равенств, получим
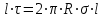 .
.После сокращения на l найдем
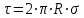 .
.С учетом этого формула (2) примет вид
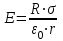 .
.Подставив это выражение в (1), получим искомую силу
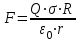 . (3)
. (3)Учтем, что
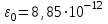 Ф/м, и подставим в (3) числовые значения величин:
Ф/м, и подставим в (3) числовые значения величин: