Файл: Курс лекций санктпетербург 2002 Министерство образования рф.doc

Точка пересечения (M) прямой линии с горизонтальной плоскостью проекций называется горизонтальным следом прямой; точка пересечения (N) прямой линии с фронтальной плоскостью проекций называется фронтальным следом прямой; точка пересечения (P) прямой линии с профильной плоскостью проекций называется профильным следом прямой.

Следы прямой совпадут с проекциями этих следов в той плоскости, где они расположены: М  M, N  N, P  P.

Поскольку точка М лежит в плоскости ₁, то ее фронтальная проекция М располагается на оси x, а профильная М – на оси y. Горизонтальная проекция точки N - N также располагается на оси x, а профильная проекция N лежит на оси z. Горизонтальная проекция профильного следа P лежит на оси y, а фронтальная проекция P - на оси z.

Охарактеризуем положение каждой проекции каждого из трех следов на ортогональном чертеже (рис. 23, б).

1) Построение проекций горизонтального следа:

M - фронтальная проекция горизонтального следа лежит на пересечении фронтальной проекции прямой с осью x;

М - горизонтальная проекция горизонтального следа лежит на пересечении линии проекционной связи, проведенной из проекции M перпендикулярно оси x, с горизонтальной проекцией прямой;

M - профильная проекция горизонтального следа лежит на пересечении профильной проекции прямой с осью y_3.

2) Построение проекций фронтального следа:

N - горизонтальная проекция фронтального следа лежит в точке пересечения горизонтальной проекции прямой с осью x;

N - фронтальная проекция фронтального следа лежит на пересечении фронтальной проекции прямой с линией проекционной связи, проведенной из точки N перпендикулярно оси x;

N - профильная проекция фронтального следа лежит на пересечении профильного следа прямой с осью

---

z.

3) Построение проекций профильного следа:

P - горизонтальная проекция профильного следа лежит на пересечении горизонтальной проекции прямой с осью y_1.

P - фронтальная проекция профильного следа лежит на пересечении фронтальной проекции прямой с осью z.

P
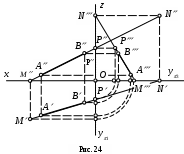
Пример 4. Построить проекции следов отрезка прямой АВ (рис. 24).
1. Находим фронтальную проекцию горизонтального следа М, продолжив АВ до пересечения с осью x.

2. Из точки М проводим линию проекционной связи до ее пересечения с продолжением АВ. Здесь расположена точка М.

3. По двум проекциям М и М строим третью - М, которая совпадает с точкой пересечения профильной проекции прямой с осью y_3.

4. Находим горизонтальную проекцию фронтального следа N в пересечении АВ с осью x.

5. Через точку N проводим линию проекционной связи до ее пересечения с фронтальной проекцией прямой AB и получаем точку N.


 - профильная проекция профильного следа находится в точке пересечения профильной проекции прямой с линией проекционной связи, проведенной из P перпендикулярно оси z.



6. По двум проекциям фронтального следа N и N строим третью его проекцию - N, которая совпадает с точкой пересечения профильной проекции прямой с осью z.

7. В пересечении АВ с осью y_1 строим точку Р (горизонтальную проекцию профильного следа).

8. В пересечении АВ с осью z получаем точку фронтальную проекцию профильного следа -

---

Р.

9. По двум проекциям Р и Р строим профильную проекцию - Р (проекции Р и Р находятся на горизонтальной линии проекционной связи).
ВЗАИМНОЕ ПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ
Две прямые могут пересекаться, быть параллельными друг другу и скрещиваться.

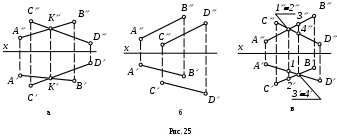
1) Пересекающиеся прямые имеют одну общую точку. Если прямые линии пересекаются, то одноименные проекции этих прямых тоже пересекаются (рис. 25, а), причем проекции точки пересечения лежат на одной линии проекционной связи.

2) Параллельные прямые лежат в одной плоскости и не имеют общих точек. Одноименные проекции двух параллельных прямых параллельны между собой (рис. 25, б).

3) Скрещивающиеся прямые, в отличие от пересекающихся и параллельных прямых, не лежат в одной плоскости. Хотя одноименные проекции двух скрещивающихся прямых и могут пересекаться, но точки их пересечения не могут лежать на одной линии проекционной связи (рис. 25, в).

Две точки, лежащие на скрещивающихся прямых и на одном перпендикуляре к плоскости проекций, называются конкурирующими. Проекции конкурирующих точек лежат в точке пересечения одноименных проекций скрещивающихся прямых (точки 1 и 2 на фронтальной плоскости проекций, точки 3 и 4 на горизонтальной плоскости проекций – см. рис. 25, в).

Построение их проекций применяется для определения взаимнойвидимостигеометрических элементов¹.




ПРОЕЦИРОВАНИЕ ПЛОСКИХ УГЛОВ
Плоский угол проецируется на плоскость проекций без искажения, если плоскость угла параллельна плоскости проекций, или иначе: плоский угол проецируется на плоскость проекций без искажения, если стороны угла параллельны плоскости проекций.

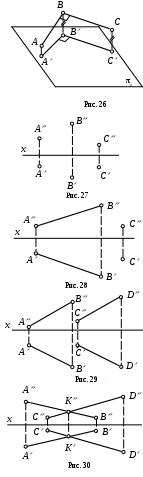
Это справедливо в отношении любого угла – острого или тупого. Исключение составляет только прямой угол, который проецируется на плоскость проекций без искажения, если хотя бы одна его сторона параллельна плоскости проекций (рис. 26).





ПРОЕЦИРОВАНИЕ ПЛОСКОСТИ
Положение плоскости в пространстве однозначно определяется положением трех ее точек.

На эпюре, следовательно, плоскость может быть задана следующими способами:

а) проекциями трех точек, не лежащих на одной прямой (рис. 27);

б) проекциями прямой и точки вне этой прямой (рис. 28);

в) проекциями двух параллельных прямых (рис. 29);

г) проекциями двух пересекающихся прямых (рис. 30);

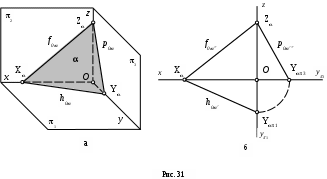
д) следами плоскости (рис. 31, а).

Прямые, по которым плоскость пересекается с плоскостями проекций, называются следами плоскости. Следы плоскости принято обозначать строчными буквами греческого алфавита.

В общем случае у плоскости будет три следа:

горизонтальный – h_0;

фронтальный – f_0;

профильный – p_0.

Точки на осях координат, в которых пересекаются следы плоскости - Х_, _ и _, называются точками схода следов, а координатные отрезки ОХ_, О_, О_ - параметрами плоскости.

Три параметра плоскости однозначно определяют положение плоскости в пространстве. Зная параметры плоскости, можно изобразить плоскость и на эпюре (рис. 31, б). Но, учитывая, что на эпюре мы изображаем только проекции геометрических элементов, то и следы плоскости мы задаем проекциями следов,

---

(которые совпадают с самими следами), которые обозначаются соответственно h_0, f_0 и p_0. Каждый след плоскости проходит через две точки схода следов. Следовательно, любые два следа плоскости позволяют определить все три параметра плоскости.



Таким образом, любые два следа плоскости однозначно определяют ее положение в пространстве. Также как положение точки в пространстве определяются тремя ее координатами, так и положение плоскости может быть задано аналитически тремя ее параметрами.

Плоскость, пересекающая все три плоскости проекций, называется плоскостью общего положения. Если плоскость параллельна одной или двум осям координат, то она называется плоскостью частного положения.


ПЛОСКОСТИ ЧАСТНОГО ПОЛОЖЕНИЯ

Плоскости, параллельные одной оси координат

1. 
   Плоскость, параллельная оси z (рис. 32).
   

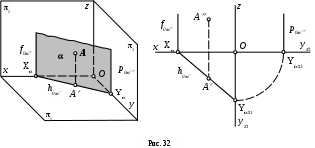
У такой плоскости параметры Х_, и _ - конечные величины, а параметр _ = . Следовательно, фронтальный и профильный следы такой плоскости, которые должны пройти через точку схода следов _, будут параллельны оси z. Плоскость, параллельная оси z перпендикулярна горизонтальной плоскости проекций и называется горизонтально-проецирующей плоскостью.

Рассмотрим точку А, лежащую в горизонтально-проецирующей плоскости , и построим горизонтальную проекцию этой точки. Для этого из точки А опустим перпендикуляр на плоскость проекций ₁. Горизонтальная проекция любой точки, лежащей в горизонтально-проецирующей плоскости, будет всегда располагаться на горизонтальном следе плоскости.

4. 
   Плоскость, параллельная оси y (рис. 33).
   

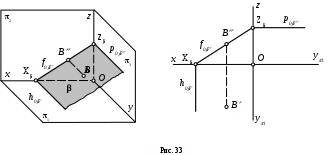
Если плоскость параллельна оси y, то ее параметр по этой оси равен бесконечности (Y_ = ) и, следовательно, горизонтальный и профильный следы плоскости будут параллельны оси y. Плоскость, параллельная оси y, перпендикулярна фронтальной плоскости проекций ₂ и называется фронтально-проецирующей плоскостью.

Фронтальная проекция любой точки, лежащей в этой плоскости (например, точки В), всегда расположена на фронтальном следе плоскости.

---

4. 
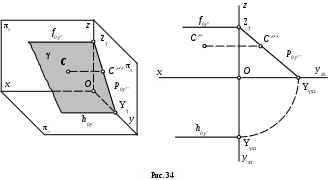
   Плоскость, параллельная оси x (рис. 34).
   

У такой плоскости параметр по оси x равен бесконечности (Х_{ =} ), поэтому ее фронтальный и горизонтальный следы будут параллельны оси x. Такая плоскость перпендикулярна профильной плоскости проекций ₃ и называется профильно-проецирующей плоскостью.

Профильная проекция любой точки, лежащей в этой плоскости (например, точки С), всегда расположена на профильном следе плоскости.

---