Файл: Курс лекций санктпетербург 2002 Министерство образования рф.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 144
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Тпроецируется в точку, которая совпадает с проекцией пересечения горизонтальных следов плоскостей - М(рис. 57,а).
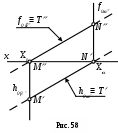
9)Проекции линии пересечения Т (Т , Т) горизонтально-проецирующей плоскости α (h0α, f0α) с фронтально-проецирующей плоскостью β (h0β, f0β) совпадают с соответствующими следами этих плоскостей (h0≡ Т и f0≡ Т )(рис. 58).
1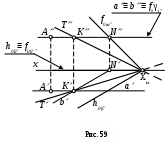
Осевая плоскость β задана следами (h0β и f0β) и точкой А (А, А), лежащей в плоскости. Вспомогательная горизонтальная плоскость γ1 ( f0γ1) проводится через точку А (А, А). При этом плоскость γ1 пересечет плоскости α и β по горизонталям этих плоскостей a (a, a) и b (b, b). Точка пересечения этих горизонталей K (K, K) является общей точкой для плоскостей α и β. На точке K (K, K) и точке пересечения следов плоскостей, совпадающей с точкой
X , строится линия пересечения плоскостей - T (T, T).
ПРЯМАЯ, ПЕРЕСЕКАЮЩАЯ ПЛОСКОСТЬ
П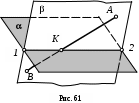
рямая, пересекающая плоскость, имеет с ней одну общую точку, называемую точкой встречи прямой с плоскостью.
Р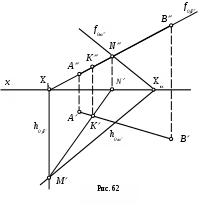
ассмотрим задачу о нахождении точки встречи прямой линии с плоскостью в общем виде (рис. 61). Пусть нам дана плоскость и прямая АВ, ее пересекающая. Проведем через прямую АВ любую плоскость, например, плоскость . Далее построим линию пересечения плоскости и - прямую 1-2. Все точки этой прямой являются общими для обеих плоскостей. Следовательно, и точка К, лежащая на прямой АВ, принадлежит обеим плоскостям. Точка К и будет искомой точкой встречи прямой АВ с плоскостью .
Рассмотрим порядок действий по нахождению точки встречи прямой АВ с плоскостью на эпюре (рис. 62):
1) Через заданную прямую АВ проводим любую вспомогательную плоскость (удобнее, если это будет плоскость частного положения – например, фронтально-проецирующая плоскость ).
2) Находим линию пересечения плоскостей и - прямую MN.
3) Горизонтальная проекция К искомой точки встречи лежит в пересечении горизонтальных проекций прямой АВ и линии пересечения MN.
4) В пересечении линии проекционной связи, проведенной из К, и фронтальной проекции прямой получаем К.
ОПРЕДЕЛЕНИЕ ВЗАИМНОЙ ВИДИМОСТИ
ГЕОМЕТРИЧЕСКИХ ЭЛЕМЕНТОВ
Взаимная видимость геометрических элементов определяет позиционное отношение одной геометрической фигуры (прямой, плоскости и т.д.) по отношению к другой в определенном направлении. Обычно это направление перпендикулярно плоскости проекций.
Взаимная видимость на эпюре определяется с помощью конкурирующих точек1, которые выбираются на той плоскости проекций, в направлении на которую определяется взаимная видимость. Конкурирующими точками называются точки, принадлежащие двум разным элементам проекции которых в одной плоскости проекций сливаются, а в другой плоскости проекций – расходятся по линии проекционной связи. Взаимная видимость в направлении на каждую из плоскостей проекций определяется отдельно.
Р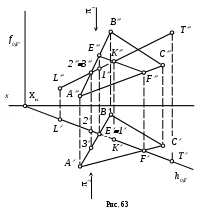
ассмотрим определение взаимной видимости прямой LТ и плоскости, заданной треугольником АВС (рис. 63). Будем считать плоскость треугольника непрозрачной. Прежде всего найдем точку пересечения прямой LТ с плоскостью треугольника. Через прямую LТ проведем вспомогательную плоскость и построим линию пересечения плоскости и плоскости треугольника АВС – прямую EF . Найдем искомую точку К. Затем определяем взаимную видимость в направлении на плоскости проекций 1 и 2.
Для определения видимости в направлении на плоскость 1 выбираем конкурирующие точки, например, Е и 1 (E1). Эти точки принадлежат разным геометрическим фигурам (Е АВ; 1 LТ), но они расположены на одной проецирующей прямой, перпендикулярной плоскости 1, поэтому на эту плоскость они проецируются в одну точку. Находим фронтальную проекцию точки 1 - 1 (проекция Е уже была найдена при предыдущих построениях).
Из двух точек видимой будет та, фронтальная проекция которой расположена дальше от оси координат. В нашем примере – это точка Е. Следовательно, на горизонтальной проекции видимой будет прямая АВ, принадлежащая плоскости треугольника, а прямая
LК – “невидима”. В точке К прямая LТ пересекает плоскость и отрезок КT cтанет видимым.
Для определения взаимной видимости в направлении на 2 выбираем на ней проекции конкурирующих точек. Пусть это будут точки 2 и 3 (23). Находим их горизонтальные проекции и определяем по ним взаимную видимость точек. Дальше от оси x будет точка 3, принадлежащая АВС. Следовательно отрезок LК - «невидим».
ПРОЕЦИРОВАНИЕ ПЛОСКИХ ФИГУР
Плоской фигурой называется такая фигура, все точки которой лежат в одной плоскости и ограничены линиями, составляющими контур этой фигуры. Простейшей плоской фигурой является многоугольник.
Д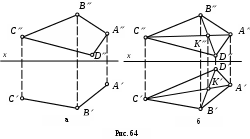
ля определения однозначного положения в пространстве многоугольника необходимо убедиться, чтобы все точки этой фигуры находились в одной плоскости.
Н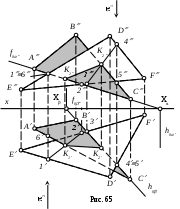
апример, четырехугольник может быть задан двумя проекциями трех его вершин и лишь одной проекцией четвертой вершины (рис. 64). Недостающая проекция вершины лежит на пересечении линии проекционной связи, проведенной из имеющейся проекции вершины многогранника, и проекции диагонали, проходящей, в свою очередь, через точку пересечения диагоналей K(K, K).
ПЕРЕСЕЧЕНИЕ ПЛОСКИХ ФИГУР
Линия пересечения двух плоских фигур, как и линия пересечения двух плоскостей определяется двумя точками, общими для этих фигур. Такие точки могут быть найдены как точки пересечения сторон одной фигуры с плоскостью другой.
На рис. 65 найдена линия пересечения двух треугольников АВС и EDF. Для этого выполнены следующие построения.
Находим точку K1 (K1, K1) пересечения стороны AC одного треугольника с плоскостью другого треугольника:
K1 = AC (∆ EDF).
Аналогично находим точку K2 (K2, K2) пересечения другой стороны, например, ВC треугольника EDF:
K2 = ВC (∆ EDF).
Зная две точки, общие для заданных плоскостей (∆ АВС) и (∆ EDF), проводим через них линию пересечения этих плоскостей K1K2 (K1K2 и K1K2).
Определяем видимость плоскостей друг относительно друга с помощью конкурирующих точек, например, точек
4 и 5 – на горизонтальной плоскости проекций (4 (DF), 5 (BC)) и точек 1 и 6 – на фронтальной плоскости проекций (1 (ED),
6 (AC).
ПРЯМАЯ, ПЕРПЕНДИКУЛЯРНАЯ ПЛОСКОСТИ
Предположим, что дана некоторая плоскость и прямая АК – перпендикуляр к этой плоскости, причем точка К является основанием перпендикуляра (рис. 66).
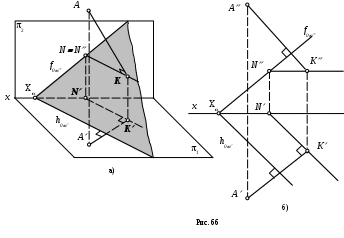
Если прямая АК – перпендикуляр, то она перпендикулярна любой прямой, принадлежащей этой плоскости.
Через точку К проведем горизонталь КN. Угол АКN – прямой. По теореме о том, что прямой угол проецируется на плоскость проекций без искажения, если хотя бы одна его сторона параллельна плоскости проекций, угол АКN - тоже прямой.
Таким образом, горизонтальная проекция перпендикуляра перпендикулярна горизонтальной проекции горизонтали и горизонтальному следу плоскости.
Аналогично можно доказать, что фронтальная проекция перпендикуляра перпендикулярна фронтальной проекции фронтали и фронтальному следу плоскости.
Пример 6. Из точки К опустить перпендикуляр к плоскости, заданной следами (рис. 67), и к плоскости, заданной треугольником (рис. 68).
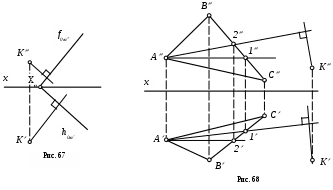
1. Из точки K проводим перпендикуляр к плоскости , заданной следами, (рис. 67): горизонтальная проекция перпендикуляра перпендикулярна горизонтальному следу плоскости h0; фронтальная проекция перпендикуляра перпендикулярна фронтальному следу плоскости f0.
2. Из точки K проводим перпендикуляр к плоскости, заданной треугольником АВС, (рис. 68).
Строим горизонталь А1 (А1, А1) и фронталь А2 (А2, А2) заданной плоскости.
Из точки К, проводим перпендикуляр к заданной плоскости: горизонтальная проекция перпендикуляра перпендикулярна горизонтальной проекции горизонтали А1; фронтальная проекция перпендикуляра перпендикулярна фронтальной проекции фронтали А2.
-
Линия пересечения Т фронтально-проецирующихплоскостей α (h0α, f0α) и β (h0β, f0β) представляет собой фронтально-проецирующую прямую, горизонтальная проекция Т которой параллельна горизонтальным следам плоскостей и проходит через проекцию N, а фронтальная проекция Т проецируется в точку, которая совпадает с проекцией пересечения фронтальных следов плоскостей - N(рис. 57, б).
9)Проекции линии пересечения Т (Т , Т) горизонтально-проецирующей плоскости α (h0α, f0α) с фронтально-проецирующей плоскостью β (h0β, f0β) совпадают с соответствующими следами этих плоскостей (h0≡ Т и f0≡ Т )(рис. 58).
1
Осевая плоскость β задана следами (h0β и f0β) и точкой А (А, А), лежащей в плоскости. Вспомогательная горизонтальная плоскость γ1 ( f0γ1) проводится через точку А (А, А). При этом плоскость γ1 пересечет плоскости α и β по горизонталям этих плоскостей a (a, a) и b (b, b). Точка пересечения этих горизонталей K (K, K) является общей точкой для плоскостей α и β. На точке K (K, K) и точке пересечения следов плоскостей, совпадающей с точкой
X , строится линия пересечения плоскостей - T (T, T).
-
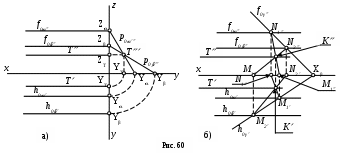
Линия пересечения T (T, T) двух профильно-проецирующих плоскостей α и β, заданных их горизонтальными (h0α,h0β)и фронтальными (f0α, f0β) следами может быть построена двумя способами:
-
либо с использованием профильной плоскости проекций (рис. 60, а), -
либо при помощи вспомогательной плоскости, в качестве которой может быть применена как плоскость частного положения, так и плоскость общего положения (рис. 60, б).
ПРЯМАЯ, ПЕРЕСЕКАЮЩАЯ ПЛОСКОСТЬ
П
рямая, пересекающая плоскость, имеет с ней одну общую точку, называемую точкой встречи прямой с плоскостью.
Р
ассмотрим задачу о нахождении точки встречи прямой линии с плоскостью в общем виде (рис. 61). Пусть нам дана плоскость и прямая АВ, ее пересекающая. Проведем через прямую АВ любую плоскость, например, плоскость . Далее построим линию пересечения плоскости и - прямую 1-2. Все точки этой прямой являются общими для обеих плоскостей. Следовательно, и точка К, лежащая на прямой АВ, принадлежит обеим плоскостям. Точка К и будет искомой точкой встречи прямой АВ с плоскостью . Рассмотрим порядок действий по нахождению точки встречи прямой АВ с плоскостью на эпюре (рис. 62):
1) Через заданную прямую АВ проводим любую вспомогательную плоскость (удобнее, если это будет плоскость частного положения – например, фронтально-проецирующая плоскость ).
2) Находим линию пересечения плоскостей и - прямую MN.
3) Горизонтальная проекция К искомой точки встречи лежит в пересечении горизонтальных проекций прямой АВ и линии пересечения MN.
4) В пересечении линии проекционной связи, проведенной из К, и фронтальной проекции прямой получаем К.
ОПРЕДЕЛЕНИЕ ВЗАИМНОЙ ВИДИМОСТИ
ГЕОМЕТРИЧЕСКИХ ЭЛЕМЕНТОВ
Взаимная видимость геометрических элементов определяет позиционное отношение одной геометрической фигуры (прямой, плоскости и т.д.) по отношению к другой в определенном направлении. Обычно это направление перпендикулярно плоскости проекций.
Взаимная видимость на эпюре определяется с помощью конкурирующих точек1, которые выбираются на той плоскости проекций, в направлении на которую определяется взаимная видимость. Конкурирующими точками называются точки, принадлежащие двум разным элементам проекции которых в одной плоскости проекций сливаются, а в другой плоскости проекций – расходятся по линии проекционной связи. Взаимная видимость в направлении на каждую из плоскостей проекций определяется отдельно.
Р
ассмотрим определение взаимной видимости прямой LТ и плоскости, заданной треугольником АВС (рис. 63). Будем считать плоскость треугольника непрозрачной. Прежде всего найдем точку пересечения прямой LТ с плоскостью треугольника. Через прямую LТ проведем вспомогательную плоскость и построим линию пересечения плоскости и плоскости треугольника АВС – прямую EF . Найдем искомую точку К. Затем определяем взаимную видимость в направлении на плоскости проекций 1 и 2. Для определения видимости в направлении на плоскость 1 выбираем конкурирующие точки, например, Е и 1 (E1). Эти точки принадлежат разным геометрическим фигурам (Е АВ; 1 LТ), но они расположены на одной проецирующей прямой, перпендикулярной плоскости 1, поэтому на эту плоскость они проецируются в одну точку. Находим фронтальную проекцию точки 1 - 1 (проекция Е уже была найдена при предыдущих построениях).
Из двух точек видимой будет та, фронтальная проекция которой расположена дальше от оси координат. В нашем примере – это точка Е. Следовательно, на горизонтальной проекции видимой будет прямая АВ, принадлежащая плоскости треугольника, а прямая
LК – “невидима”. В точке К прямая LТ пересекает плоскость и отрезок КT cтанет видимым.
Для определения взаимной видимости в направлении на 2 выбираем на ней проекции конкурирующих точек. Пусть это будут точки 2 и 3 (23). Находим их горизонтальные проекции и определяем по ним взаимную видимость точек. Дальше от оси x будет точка 3, принадлежащая АВС. Следовательно отрезок LК - «невидим».
ПРОЕЦИРОВАНИЕ ПЛОСКИХ ФИГУР
Плоской фигурой называется такая фигура, все точки которой лежат в одной плоскости и ограничены линиями, составляющими контур этой фигуры. Простейшей плоской фигурой является многоугольник.
Д
ля определения однозначного положения в пространстве многоугольника необходимо убедиться, чтобы все точки этой фигуры находились в одной плоскости. Н
апример, четырехугольник может быть задан двумя проекциями трех его вершин и лишь одной проекцией четвертой вершины (рис. 64). Недостающая проекция вершины лежит на пересечении линии проекционной связи, проведенной из имеющейся проекции вершины многогранника, и проекции диагонали, проходящей, в свою очередь, через точку пересечения диагоналей K(K, K).ПЕРЕСЕЧЕНИЕ ПЛОСКИХ ФИГУР
Линия пересечения двух плоских фигур, как и линия пересечения двух плоскостей определяется двумя точками, общими для этих фигур. Такие точки могут быть найдены как точки пересечения сторон одной фигуры с плоскостью другой.
На рис. 65 найдена линия пересечения двух треугольников АВС и EDF. Для этого выполнены следующие построения.
Находим точку K1 (K1, K1) пересечения стороны AC одного треугольника с плоскостью другого треугольника:
K1 = AC (∆ EDF).
Аналогично находим точку K2 (K2, K2) пересечения другой стороны, например, ВC треугольника EDF:
K2 = ВC (∆ EDF).
Зная две точки, общие для заданных плоскостей (∆ АВС) и (∆ EDF), проводим через них линию пересечения этих плоскостей K1K2 (K1K2 и K1K2).
Определяем видимость плоскостей друг относительно друга с помощью конкурирующих точек, например, точек
4 и 5 – на горизонтальной плоскости проекций (4 (DF), 5 (BC)) и точек 1 и 6 – на фронтальной плоскости проекций (1 (ED),
6 (AC).
ПРЯМАЯ, ПЕРПЕНДИКУЛЯРНАЯ ПЛОСКОСТИ
Предположим, что дана некоторая плоскость и прямая АК – перпендикуляр к этой плоскости, причем точка К является основанием перпендикуляра (рис. 66).
Если прямая АК – перпендикуляр, то она перпендикулярна любой прямой, принадлежащей этой плоскости.
Через точку К проведем горизонталь КN. Угол АКN – прямой. По теореме о том, что прямой угол проецируется на плоскость проекций без искажения, если хотя бы одна его сторона параллельна плоскости проекций, угол АКN - тоже прямой.
Таким образом, горизонтальная проекция перпендикуляра перпендикулярна горизонтальной проекции горизонтали и горизонтальному следу плоскости.
Аналогично можно доказать, что фронтальная проекция перпендикуляра перпендикулярна фронтальной проекции фронтали и фронтальному следу плоскости.
Пример 6. Из точки К опустить перпендикуляр к плоскости, заданной следами (рис. 67), и к плоскости, заданной треугольником (рис. 68).
1. Из точки K проводим перпендикуляр к плоскости , заданной следами, (рис. 67): горизонтальная проекция перпендикуляра перпендикулярна горизонтальному следу плоскости h0; фронтальная проекция перпендикуляра перпендикулярна фронтальному следу плоскости f0.
2. Из точки K проводим перпендикуляр к плоскости, заданной треугольником АВС, (рис. 68).
Строим горизонталь А1 (А1, А1) и фронталь А2 (А2, А2) заданной плоскости.
Из точки К, проводим перпендикуляр к заданной плоскости: горизонтальная проекция перпендикуляра перпендикулярна горизонтальной проекции горизонтали А1; фронтальная проекция перпендикуляра перпендикулярна фронтальной проекции фронтали А2.