Файл: Организация медикосоциальных исследований и методы статистического анализа Модуль Абсолютные и относительные статистические показатели Цель изучения модуля.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 217
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
; 
;
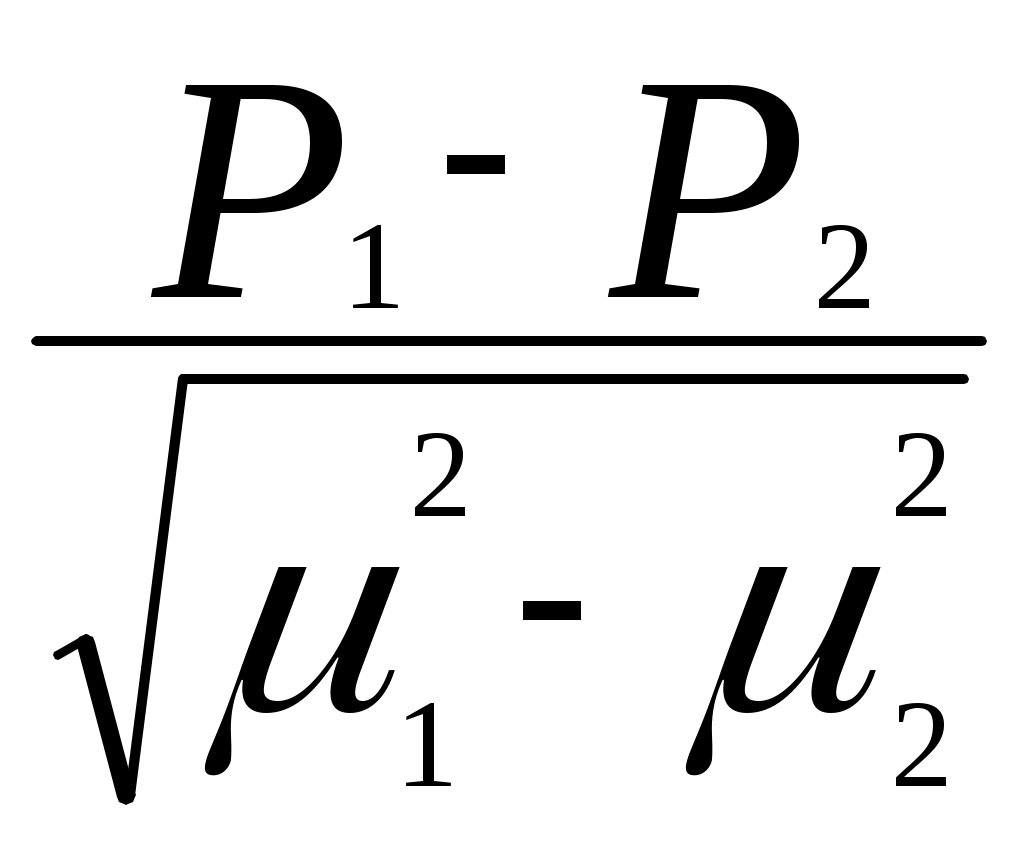12.НАЗОВИТЕ значениЕ Т С НАДЕЖНОСТЬЮ γ = 0,9544, ПРИ КОТОРОМ можно утверждать, что между сравниваемыми величинами (средними или вероятностями) имеются существенные различия
1. 1,0;
2. 1,5;
3. 2,0;
4. 2,5;
5. 3,0
13. Каким образом при заданной надежности можно уменьшить доверительный интервал для оцениваемого параметра генеральной совокупности?
1. Использовать другие методы оценки достоверности;
2. Увеличить число наблюдений;
3. Использовать другие способы формирования выборочной совокупности;
4. Изучить структуру генеральной совокупности;
5. Провести априорный (разведочный) анализ данных.
5.6. Задачи для самостоятельного решения
Задача 1
Исходные данные
1. При изучении воздействия физических нагрузок на организм было установлено, что средний уровень максимального артериального давления у 78 спортсменов через 10 минут после прекращения занятий составил 132 мм. рт. ст. σ = 12,4 мм. рт. ст.
2. Среди 200 больных туберкулезом после шестимесячного лечения антибактериальными препаратами у 70 больных была отмечена положительная реакция на БК (БК+).
3. При изучении средней массы тела детей двух детских садов установлено, что в детском саду №1: M1 = 25 кг;
2 = 0,24 кг, в детском саду №2: М2 = 23,1 кг; 1 = 0,15 кг
4. При изучении уровня заболеваемости на двух педиатрических участках установлено, что на участке 1: ω1=0,026, 1 = 2,4, на участке 2: ω2 = 0,018, 2 = 2,0.
Задание
На основании исходных данных:
1. Рассчитать среднюю ошибку (
) и доверительные границы средней генеральной совокупности (Мген).
2. Рассчитать среднюю ошибку (
) и доверительные границы вероятности (Рген).
3. Оценить значимость различия средней массы тела детей в детском саду №1 и №2.
4. Оценить значимость различия уровня заболеваемости на двух педиатрических участках.
Задача 2
Исходные данные
1. Средний рост 125 подростков одной из школ города 168 см, σ = 2,4 см.
2. У 1220 работающих в течение года было зарегистрировано 980 случаев временной утраты трудоспособности.
3. При изучении средней длины окружности грудной клетки у мужчин в возрасте 20 лет, занимающихся и не занимающихся спортом установлено, что у занимающихся спортом - M1 = 102 см; 1 = 4,5 см, у не занимающихся спортом - М2 = 78,3 см; 2 = 2,1 см.
4. При изучении уровня заболеваемости с временной утратой трудоспособности в двух цехах промышленного предприятия, что в цехе 1: ω1 = 0,94; 1 = 4,2, в цехе 2: ω2=0,72; 2 = 2,4.
Задание
На основании исходных данных:
1. Рассчитать среднюю ошибку ( ) и доверительные границы среднего генеральной совокупности (Мген).
2. Рассчитать среднюю ошибку ( ) и доверительные границы вероятности (Рген).
3. Оценить значимость различия средней длины окружности грудной клетки у мужчин, занимающихся и не занимающихся спортом.
4. Оценить значимость различия уровня заболеваемости с временной утратой трудоспособности в двух цехах.
Задача 3
Исходные данные
1. При изучении воздействия физических нагрузок на организм было установлено, что средняя масса 116 спортсменов составила 74 кг, σ = 4,2 кг.
2. После проведенного комплексного медицинского осмотра среди 1850 осмотренных было выявлено 562 случая заболеваний в ранней стадии.
3. При изучении средней массы тела подростков в двух школах установлено, что в школе 1: М1 = 62,7кг;
1= 3,4 кг, в школе 2: М2 = 52,4 кг; 2 = 2,1 кг.
4. При изучении уровня послеоперационной летальности в двух больницах А и Б установлено, что в больнице 1: ω1 = 0,035; 1= 1,3, в больнице 2: ω2 = 0,024; 2= 0,82.
Задание
На основании исходных данных:
1. Рассчитать среднюю ошибку ( ) и доверительные границы среднего генеральной совокупности (Мген).
2. Рассчитать среднюю ошибку ( ) и доверительные границы вероятности (Рген).
3. Оценить значимость различия среднего роста подростков в двух школах.
4. Оценить значимость различия уровня послеоперационной летальности в двух больницах А и Б.
5.7. Рекомендуемая литература
Задание
На основе исходных данных, представленных в таблице:
1. Рассчитать общие и возрастные коэффициенты заболеваемости на территориях А и Б.
2. Рассчитать стандартизованные коэффициенты заболеваемости.
3. Сравнить уровень смертности на территориях А и Б с помощью стандартизованных коэффициентов заболеваемости.
6.7. Рекомендуемая литература
Модуль 7. Временные ряды
Цель изучения модуля: показать использование временных рядов для анализа общественного здоровья, деятельности системы (организаций) здравоохранения и в клинической практике.
После изучения темы студент должен знать:
Студент должен уметь:
Временной ряд – это последовательность числовых значений статистического показателя y(t), записанных в хронологическом порядке. Временной ряд также называют динамическим или хронологическим рядом.
Уровни ряда – числовые значения статистического показателя временного ряда. Таким образом, временной ряд представляет собой последовательность уровней: y0, y1, y2, …, yn. При этом выделяют начальный (базисный) уровень - y0 и конечный уровень ряда - yn.
Временные ряды можно представить в виде таблиц и в виде графика (рис. 7.1).
Таблица 7.1. Временные ряды абсолютного числа родившихся и умерших в возрасте до 1 года в РФ (1975-2015)
Таблица 7.2. Временные ряды общих коэффициентов рождаемости (ОКР) и смертности (ОКС) населения РФ (1995-2015)
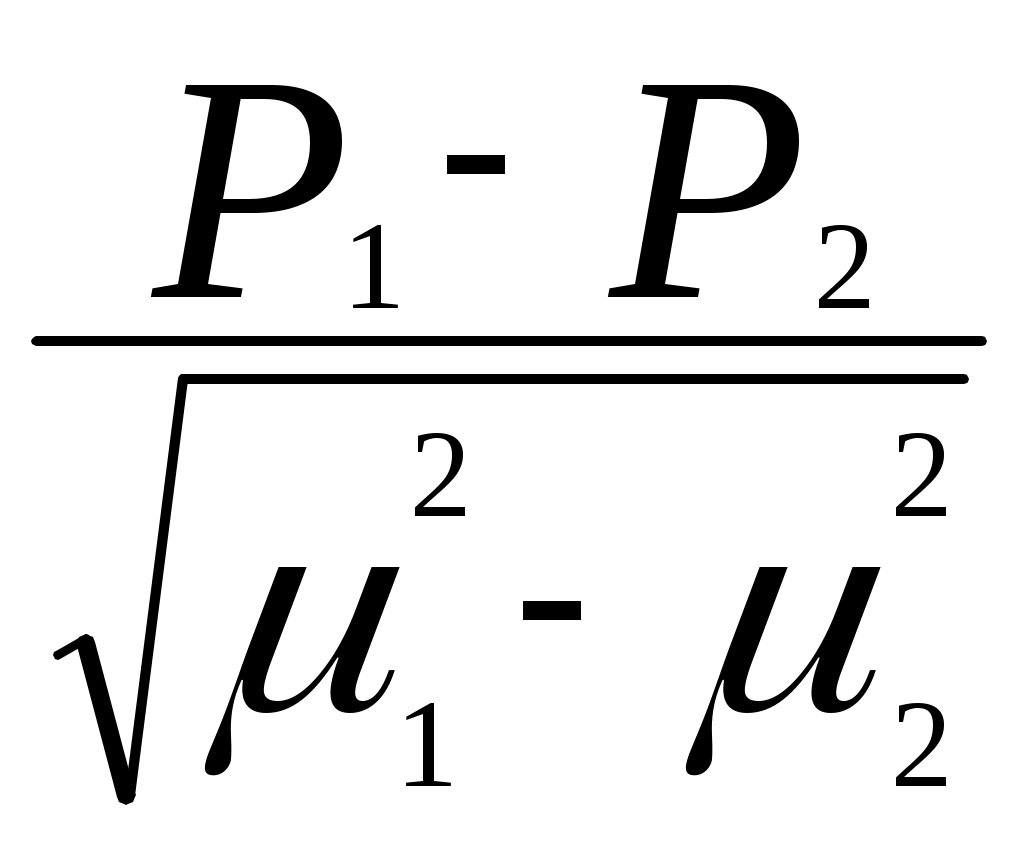;12.НАЗОВИТЕ значениЕ Т С НАДЕЖНОСТЬЮ γ = 0,9544, ПРИ КОТОРОМ можно утверждать, что между сравниваемыми величинами (средними или вероятностями) имеются существенные различия
1. 1,0;
2. 1,5;
3. 2,0;
4. 2,5;
5. 3,0
13. Каким образом при заданной надежности можно уменьшить доверительный интервал для оцениваемого параметра генеральной совокупности?
1. Использовать другие методы оценки достоверности;
2. Увеличить число наблюдений;
3. Использовать другие способы формирования выборочной совокупности;
4. Изучить структуру генеральной совокупности;
5. Провести априорный (разведочный) анализ данных.
5.6. Задачи для самостоятельного решения
Задача 1
Исходные данные
1. При изучении воздействия физических нагрузок на организм было установлено, что средний уровень максимального артериального давления у 78 спортсменов через 10 минут после прекращения занятий составил 132 мм. рт. ст. σ = 12,4 мм. рт. ст.
2. Среди 200 больных туберкулезом после шестимесячного лечения антибактериальными препаратами у 70 больных была отмечена положительная реакция на БК (БК+).
3. При изучении средней массы тела детей двух детских садов установлено, что в детском саду №1: M1 = 25 кг;
2 = 0,24 кг, в детском саду №2: М2 = 23,1 кг; 1 = 0,15 кг4. При изучении уровня заболеваемости на двух педиатрических участках установлено, что на участке 1: ω1=0,026,
1 = 2,4, на участке 2: ω2 = 0,018, 2 = 2,0.Задание
На основании исходных данных:
1. Рассчитать среднюю ошибку (
) и доверительные границы средней генеральной совокупности (Мген).2. Рассчитать среднюю ошибку (
) и доверительные границы вероятности (Рген).3. Оценить значимость различия средней массы тела детей в детском саду №1 и №2.
4. Оценить значимость различия уровня заболеваемости на двух педиатрических участках.
Задача 2
Исходные данные
1. Средний рост 125 подростков одной из школ города 168 см, σ = 2,4 см.
2. У 1220 работающих в течение года было зарегистрировано 980 случаев временной утраты трудоспособности.
3. При изучении средней длины окружности грудной клетки у мужчин в возрасте 20 лет, занимающихся и не занимающихся спортом установлено, что у занимающихся спортом - M1 = 102 см;
1 = 4,5 см, у не занимающихся спортом - М2 = 78,3 см; 2 = 2,1 см.4. При изучении уровня заболеваемости с временной утратой трудоспособности в двух цехах промышленного предприятия, что в цехе 1: ω1 = 0,94;
1 = 4,2, в цехе 2: ω2=0,72; 2 = 2,4.Задание
На основании исходных данных:
1. Рассчитать среднюю ошибку (
) и доверительные границы среднего генеральной совокупности (Мген).2. Рассчитать среднюю ошибку (
) и доверительные границы вероятности (Рген).3. Оценить значимость различия средней длины окружности грудной клетки у мужчин, занимающихся и не занимающихся спортом.
4. Оценить значимость различия уровня заболеваемости с временной утратой трудоспособности в двух цехах.
Задача 3
Исходные данные
1. При изучении воздействия физических нагрузок на организм было установлено, что средняя масса 116 спортсменов составила 74 кг, σ = 4,2 кг.
2. После проведенного комплексного медицинского осмотра среди 1850 осмотренных было выявлено 562 случая заболеваний в ранней стадии.
3. При изучении средней массы тела подростков в двух школах установлено, что в школе 1: М1 = 62,7кг;
1= 3,4 кг, в школе 2: М2 = 52,4 кг;
2 = 2,1 кг.4. При изучении уровня послеоперационной летальности в двух больницах А и Б установлено, что в больнице 1: ω1 = 0,035;
1= 1,3, в больнице 2: ω2 = 0,024; 2= 0,82.Задание
На основании исходных данных:
1. Рассчитать среднюю ошибку (
) и доверительные границы среднего генеральной совокупности (Мген).2. Рассчитать среднюю ошибку (
) и доверительные границы вероятности (Рген).3. Оценить значимость различия среднего роста подростков в двух школах.
4. Оценить значимость различия уровня послеоперационной летальности в двух больницах А и Б.
5.7. Рекомендуемая литература
-
Медик В.А. Общественное здоровье и здравоохранение: учебник. – 3-е изд., испр. и доп. – М.: ГЭОТАР-Медиа, 2017. -
Медик В.А., Токмачев М.С. Математическая статистика в медицине: учеб. пособие. - М.: Финансы и статистика, 2007. – 800 с.
| Всего | 462 000 | 663 080 | 191 300 | 247 975 | 1 |
| * В качестве стандарта взята возрастная структура населения, проживающего на территории С | |||||
Задание
На основе исходных данных, представленных в таблице:
1. Рассчитать общие и возрастные коэффициенты заболеваемости на территориях А и Б.
2. Рассчитать стандартизованные коэффициенты заболеваемости.
3. Сравнить уровень смертности на территориях А и Б с помощью стандартизованных коэффициентов заболеваемости.
6.7. Рекомендуемая литература
-
Медик В.А. Общественное здоровье и здравоохранение: учебник. – 3-е изд., испр. и доп. – М.: ГЭОТАР-Медиа, 2017. -
Медик В.А., Токмачев М.С. Математическая статистика в медицине: учеб. пособие. - М.: Финансы и статистика, 2007. – 800 с. -
Щепин О.П., Купеева И.А., Щепин В.О., Какорина Е.П. Современные региональные особенности здоровья населения и здравоохранения России. – М.: ОАО «Издательство «Медицина», издательство «Шико», 2007. – 360 с.: ил.
Модуль 7. Временные ряды
Цель изучения модуля: показать использование временных рядов для анализа общественного здоровья, деятельности системы (организаций) здравоохранения и в клинической практике.
После изучения темы студент должен знать:
-
определение понятия «временной ряд»; -
показатели, характеризующие временной ряд.
Студент должен уметь:
-
рассчитывать и анализировать показатели, характеризующие временной ряд;
-
делать заключение о тенденциях и закономерностях в изучаемом явлении на основе анализа показателей временного ряда.
7.1. Блок информации
Временной ряд – это последовательность числовых значений статистического показателя y(t), записанных в хронологическом порядке. Временной ряд также называют динамическим или хронологическим рядом.
Уровни ряда – числовые значения статистического показателя временного ряда. Таким образом, временной ряд представляет собой последовательность уровней: y0, y1, y2, …, yn. При этом выделяют начальный (базисный) уровень - y0 и конечный уровень ряда - yn.
Временные ряды можно представить в виде таблиц и в виде графика (рис. 7.1).
Таблица 7.1. Временные ряды абсолютного числа родившихся и умерших в возрасте до 1 года в РФ (1975-2015)
| Год | 1975 | 1980 | 1985 | 1990 | 1995 | 2000 | 2005 | 2010 | 2015 |
| Число родившихся (n) | 2106147 | 2202779 | 2375147 | 1 988 858 | 1 363 806 | 1 266 800 | 1460 085 | 1788948 | 1 940 579 |
| Число умерших в возрасте до 1 года (m) | 49086 | 48500 | 49381 | 35 088 | 24 840 | 19 286 | 16 236 | 13405 | 12664 |
Таблица 7.2. Временные ряды общих коэффициентов рождаемости (ОКР) и смертности (ОКС) населения РФ (1995-2015)
| Год | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 |
| ОКР | 9,3 | 8,9 | 8,6 | 8,8 | 8,4 | 8,7 | 9,1 | 9,8 | 10,3 | 10,4 | 10,2 | 10,4 | 11,3 | 12,1 | 12,4 | 12,6 | 12,6 | 13,3 | 13,2 | 13,3 | 13,3 |
| ОКС | 15,0 | 14,2 | 13,8 | 13,6 | 14,7 | 15,3 | 15,6 | 16,3 | 16,5 | 16,0 | 16,1 | 15,2 | 14,7 | 14,6 | 14,2 | 14,3 | 13,5 | 13,3 | 13,0 | 13,1 | 13,0 |