Файл: Организация медикосоциальных исследований и методы статистического анализа Модуль Абсолютные и относительные статистические показатели Цель изучения модуля.doc

1. Рождаемость.

2. Заболеваемость.

3. Средняя продолжительность предстоящей жизни.

4. Физическое здоровье.

5. Инвалидность.
3.6. Задачи для самостоятельного решения

Задача 1

Исходные данные

1. При измерении роста 10 мальчиков в возрасте 4 лет, посещающих детский сад, получены следующие значения: 104, 103, 102, 101, 100, 99, 98, 97, 96, 95 см.

2. При измерении систолического артериального давления у 64 мужчин в возрасте 23 лет получены следующие значения, представленные в таблице 3.2.
Таблица 3.2. Систолическое артериальное давление, мм рт.ст.

Уровень максимального артериального давления, xi	100	105	110	115	120	125	130	135	140
Частота, mi	2	5	6	9	15	12	8	5	2

Задание

1. На основании представленных исходных данных, рассчитать средний рост мальчиков в возрасте 4 лет.

2. На основе представленных исходных данных, рассчитать средний уровень максимального артериального давления у мужчин в возрасте 23 лет.
Задача 2

Исходные данные

1. При измерении массы тела у девочек в возрасте 12 лет, получены следующие значения: 27; 28; 29; 30; 31; 32; 33; 34; 35; 36; 37; 38; 39; 40; 41 кг

2. При измерении частоты пульса перед началом соревнований у 75 спортсменов, получены следующие значения, представленные в таблице 3.3.
Таблица 3.3. Частота пульса у спортсменов

Число ударов в минуту, xi	68	70	72	74	76	78	80	82	84	86	88	90
Частота, mi	3	4	5	8	9	10	13	11	7	2	2	1

---

Задание

1. На основании представленных исходных данных, рассчитать среднюю массу тела у девочек в возрасте 12 лет.

2. На основе представленных исходных данных, рассчитать среднюю частоту пульса у спортсменов.
Задача 3

Исходные данные

1. При выборочном обследовании санитарно-гигиенических условий 15 семей, проживающих в многоквартирном доме, получены следующие данные о числе квадратных метров, приходящихся на одного члена семьи: 5, 6, 7, 8, 9, 10, 12, 15, 16, 18, 19, 20, 22, 24,26 кв.м.

2. При измерении длины окружности груди мальчиков-подростков получены следующие значения, представленные в таблице 3.4.
Таблица 3.4. Длина окружности груди мальчиков-подростков, см

Окружность груди xi	53	54	55	56	57	58	59	60	61	62	63	64	65	66	67
Частота, mi	1	1	2	3	5	5	7	10	8	6	4	4	2	2	1

Задание

1. На основании представленных исходных данных, рассчитать среднее число квадратных метров приходящихся на одного члена семьи.

2. На основе представленных исходных данных, рассчитать среднюю длины окружности груди мальчиков.
3.7. Рекомендуемая литература

1. 
   Медик В.А. Общественное здоровье и здравоохранение: учебник. – 3-е изд., испр. и доп. – М.: ГЭОТАР-Медиа, 2017.
   
2. 
   Медик В.А., Токмачев М.С. Математическая статистика в медицине: учеб. пособие. - М.: Финансы и статистика, 2007. – 800 с.
   

Модуль 5. Оценка достоверности результатов медико-социального исследования

Цель изучения модуля: показать применение методов оценки достоверности результатов

---

исследования при изучении общественного здоровья, деятельности системы (организаций) здравоохранения и в клинической практике.

После изучения темы студент должен знать:

• 
  определение понятия достоверности результатов исследования;
  
• 
  способы оценки достоверности результатов исследования;
  
• 
  условия применения способов оценки достоверности результатов исследования.
  

Студент должен уметь:

• 
  определять достоверность результатов исследования;
  
• 
  выбирать способ оценки достоверности результатов исследования при изучении общественного здоровья, деятельности системы (организаций) здравоохранении и в клинической практике.
  

---

5.1. Блок информации

Полученные в результате выборочного исследования относительные и средние величины должны объективно характеризовать генеральную совокупность, т. е. быть достоверными.

Оценить достоверность результатов исследования означает определить, с какой вероятностью возможно перенести результаты, полученные из выборочной совокупности, на всю генеральную совокупность. Таким образом, оценка достоверности необходима для того, чтобы по части явления можно было бы судить о явлении в целом и его закономерностях.

Для оценки достоверности используют:

• определение математического ожидания, оцениваемого средним значением и определение вероятности осуществления случайного события в одном испытании, оцениваемой относительной частотой;

• определение доверительных границ;

• определение достоверности показателя разности характеристик различных совокупностей.

Средняя ошибка при оценке математического ожидания определяется по формуле:

,

где - среднее квадратическое отклонение;

n – число наблюдений.

Средняя ошибка при оценке вероятности по относительной частоте, находимой из выборки определяется как:

При числе наблюдений меньше 30 ошибки математического ожидания и вероятности, находимых по выборке, определяются соответственно по формулам:

Доверительные границы – это границы интервала при оценке математического ожидания или вероятности по относительной частоте, выход за пределы которых вследствие случайных колебаний имеет незначительную вероятность (стандартными значениями этих вероятностей считаются: 0,05; 0,01; 0,001).

Формулы определения доверительных границ:

• для средних величин (М_ген): М_выб ± t ;

• 
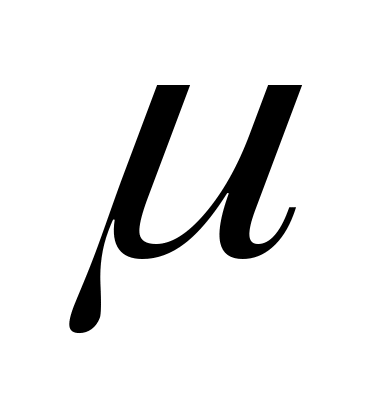  для вероятностей, находимых по частоте (Р_ген): Р_выб ±t ;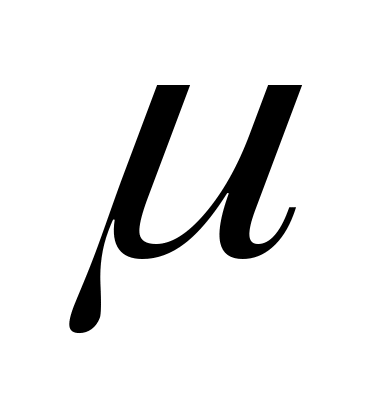
  

---

где М_ген и Р_ген соответственно - значения математического ожидания и вероятность осуществления изучаемого события в одном испытании, рассматриваемые, как параметры генеральной совокупности;

М_выб и Р_выб – соответствующие оценки, находимые по выборочной совокупности (стандартные обозначения, использованные выше), М_выб = – значение средней арифметической величины, Р_{выб =} ω – значение относительной частоты.

– средняя ошибка выборки;

t – доверительный коэффициент, зависящий от надежности γ и объема выборки n.

Надежность (доверительная вероятность) γ выбирается исследователем. Стандартные значения: γ = 0,95 и γ = 0,99. Следовательно, вероятность ошибки в найденном соотношении, определяемая как 1-γ, равна соответственно 0,05 и 0,01.

В тех случаях, когда необходимо определить, случайны или достоверны различия между двумя средними величинами или двумя вероятностями используется способ оценки достоверности разности показателей, называемый критерием значимости. Для проверки наличия или отсутствия различий в значениях показателей (проверки гипотез) используются соответствующие критерии (случайные величины):

• 
  для средних величин: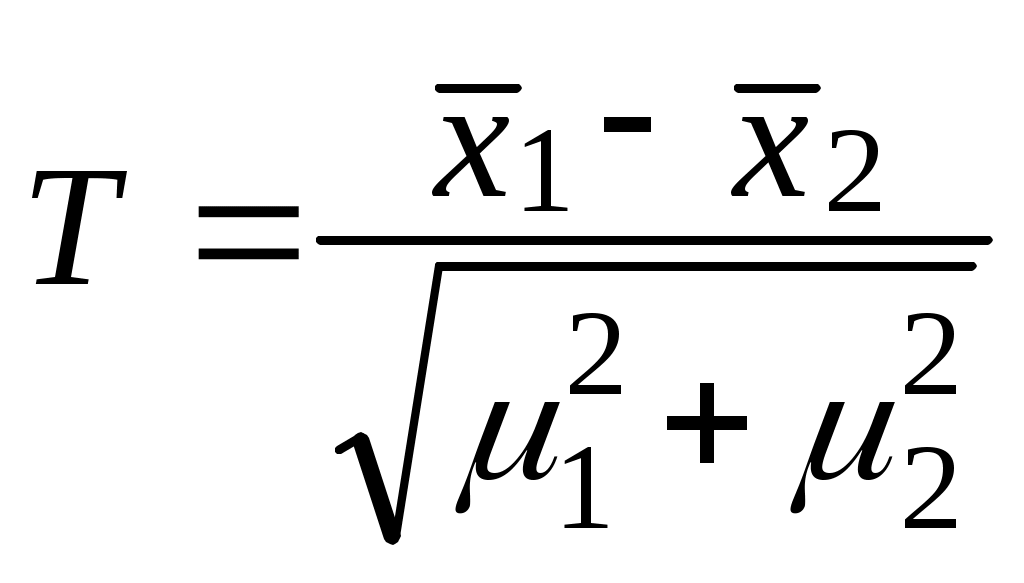
  
• 
  для вероятностей: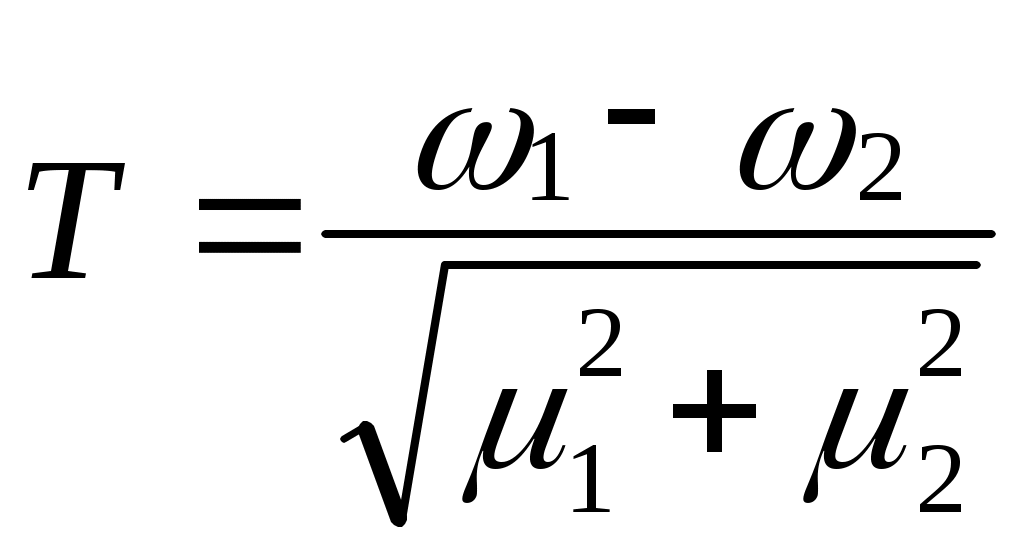
  

где ₁ и ₂ – средние ошибки показателей; и – выборочные средние величины, ω₁ и ω₂ – относительные частоты.

Если вычисленное значение критерия T по модулю более или равно 2, что соответствует надежности γ, равной 0,9544, то различие показателей следует считать достоверным (значимым).

При T<2 надежность γ меньше 0,9544. принято считать, что, в таком случае, различие случайно, т.е. не обусловлено какой-то закономерностью (различие не значимо).

Проверка предположений о характеристиках показателей по статистическим данным изучается в разделе математической статистики «Проверка статистических гипотез».

---