Файл: Учебнометодическое пособие знакомит студентов с основными понятиями о.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 476
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
х3(потребности) имеет наибольшую факторную нагрузку (1,12), а х2 (способности) — наименьшую (0,36).
Следовательно, наиболее значимой причиной, влияющей на все остальные психологические переменные, в нашем случае являются потребности, а наименее значимой — способности. Из корреляционной матрицы видно, что связи переменной х3со всеми остальными являются наиболее сильными (от 0,40 до 0,75), а корреляции переменной х2 — самыми слабыми (от 0,16 до 0,40).
Чаще всего в итоге факторного анализа определяется не один, а несколько факторов, по-разному объясняющих матрицу интеркорреляций переменных. В таком случае факторы делят на генеральные, общие и единичные.
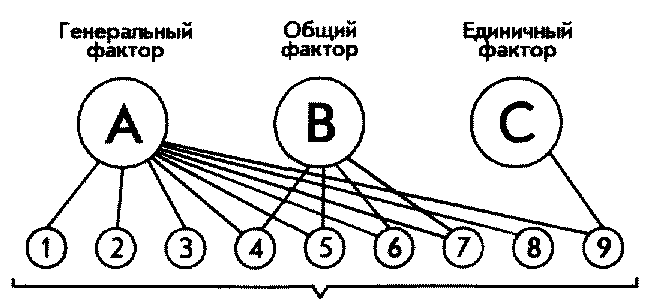
Генеральными называются факторы, все факторные нагрузки которых значительно отличаются от нуля (нуль нагрузки свидетельствует о том, что данная переменная никак не связана с остальными и не оказывает на них никакого влияния в жизни).
Общие — это факторы, у которых часть факторных нагрузок отлична от нуля.
Единичные — это факторы, в которых существенно отличается от нуля только одна из нагрузок.
Вопросы для самопроверки:
Регрессионный анализ
Довольно часто в практике исследовательской работы имеет место ситуация, когда важнейшие переменные, описывающие некоторый процесс, известны заранее, но модель процесса еще не известна. В этом случае возможны разные подходы. Одним из них является построение эмпирических моделей.
Построение эмпирических моделей предполагает проведение экспериментов или наблюдений для сбора опытных данных, выбор одной определенной модели из некоторого множества возможных, вычисление коэффициентов модели («подгонку») и оценку полученных результатов.
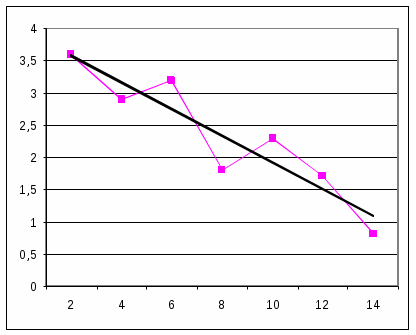
Число цветков при разном количестве неорганического брома в почве.
Метод наименьших квадратов
Метод наименьших квадратов, разработанный знаменитыми математиками К. Гауссом и А. Лежандром, берет свое начало от задач геодезии и астрономии. Рассмотрим его существо на примере линейной модели. Итак, пусть для представления полученных данных мы выбрали линейную модель y
*=a+bx, где х – независимая переменная, т. е., переменная, которую экспериментатор может менять по своему усмотрению; y* - зависимая переменная или отклик; a и b – коэффициенты (параметры). Из данных, приведенных в примере, видно, что именно такой моделью (уравнением прямой линии) может быть описана зависимость.
С другой стороны, видно что реально наблюдаемые значения отклика yi несколько отличаются от откликов yi*, соответствующих уравнению модели. И такое положение будет всегда, даже в тех случаях, когда зависимая и независимая переменные будут связаны строгой функциональной зависимостью. В этом случае отклонения эмпирических значений от теоретических связаны с погрешностями измерений, которые всегда имеют место.
Итак, каждому значению независимой переменной в общем случае соответствует ошибка: i=yi-yi*.
Естественно, что в зависимости от того, как будет проведена прямая, аппроксимирующая набор экспериментальных данных, величины i будут различны. Именно, для того, чтобы избежать субъективности при построении эмпирической модели, и был разработан метод наименьших квадратов, позволяющий однозначно определить параметры выбранной модели. В основе этого метода лежит критерий минимизации суммы квадратов ошибок, т. е. требование, чтобы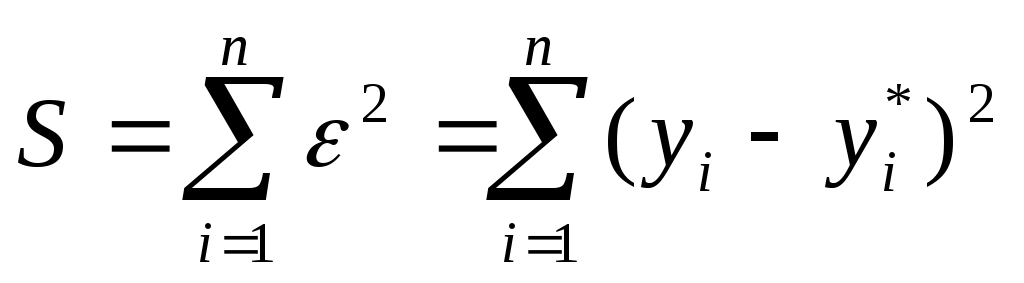
была минимальной.
Покажем, как используется метод наименьших квадратов на примере оценки параметров для уравнения y*=a+bx.
В общем случае необходимо решить систему уравнений:
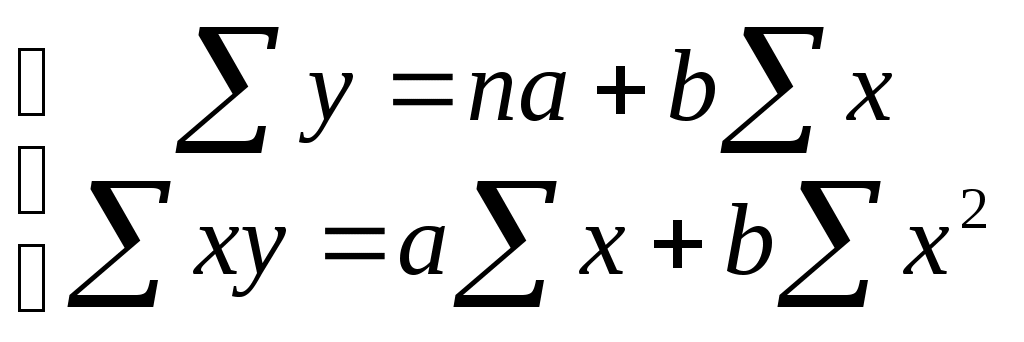, из которых находятся коэффициенты a и b.
Подставляя данные из примера, получаем:
16,3=7a+56b
107=56a+560b
Откуда a=4, b=-0,209.
В таблице приведено сравнение между реальными и теоретическими данными, а также величины ошибок.
Выбор формы функциональной зависимости
Пусть имеется ряд данных, представляющих одну зависимую и одну независмую переменную, и требуется определить функциональную связь между ними. Универсального способа решения этой задачи не существует. Иногда анализ графического изображения имеющихся данных, а также понимание механизма исследуемого процесса помогают выбрать вид аналитической зависимости. Особенно просто оценить вид функциональной зависимости, если экспериментальные данные укладываются или группируются относительно некоторой прямой.
Значительное число зависимостей, встречающихся в практике научных исследований в самых разных областях знаний, может быть описано следующими уравнениями:
y=a+bx,
y=a+bx+cx2,
y=abx,
y=axb,
y=x/(a+bx).
Применение парного линейного уравнения регрессии
Прежде чем обсуждать вопросы использования уравнений парной регрессии, вспомним, что парный корреляционный анализ не дает чистых мер влияния только одного изучаемого фактора. Если факторы взаимосвязаны, то парная связь измеряет влияние данного фактора и часть влияния прочих факторов, связанных с ним.
Уравнение регрессии применимо для прогнозирования возможных ожидаемых значений результативного признака. При этом следует учесть, что перенос закономерности связи, измеренной в варьирующей совокупности, в статике на динамику, не является, строго говоря, корректным и требует условий допустимости такого переноса (экстраполяции), что выходит за рамки статистики и может быть сделано только специалистом, хорошо знающим объект (систему) и возможности его развития в будущем).
Ограничением прогнозирования на основе регрессионного уравнения, тем более парного, служит условие стабильности или по крайней мере малой изменчивости других факторов и условий изучаемого процесса, не связанных с ними. Если резко изменится внешняя среда протекающего процесса, прежнее уравнение результативного признака на факторный потеряет свое значение. В сильно засушливый год доза удобрения может не оказать влияния на урожайность, так как последнюю лимитирует пониженная влагообеспеченность (закон Либиха).
Корреляционно-регрессионные модели (КРМ)
и их применение в анализе и прогнозе.
Корреляционно-регрессионной моделью системы взаимосвязанных признаков является такое уравнение регрессии, которое включает основные факторы, влияющие на результативный признак, обладает высоким (не ниже 0.5) коэффициентом детерминации и коэффициентами регрессии.
Приведенное определение КРМ включает достаточно строгие условия: далеко не всякое уравнение регрессии можно считать моделью.
Теория и практика выработали ряд рекомендация для построения корреляционно-регрессионной модели:
Интерпретировать корреляционные показатели строго следует лишь в терминах вариации (различий в пространстве) отклонений от средней величины. Если же задача исследования состоит в измерении связи не между вариацией двух признаков в совокупности, а между измерениями признаков объекта во времени, то метод корреляциооно-регрессионного анализа требует значительного изменения.
Из вышеприведенного определения об интерпретации показателей корреляции следует, что нельзя трактовать корреляцию признаков как связь их уровней. Это ясно хотя бы из такого примера: Если бы все студенты, которые ходят на лекции, учились бы только на пятерки, то вариация этого признака равнялась бы нулю, а следовательно успеваемость абсолютно не могла бы влиять на посещаемость. Параметры корреляции между успеваемостью и посещаемостью всегда будут равняться нулю. Но ведь и в этом случае уровень знаний зависел бы от числа лекций - он был бы тем выше, чем больше лекций.
Следовательно, наиболее значимой причиной, влияющей на все остальные психологические переменные, в нашем случае являются потребности, а наименее значимой — способности. Из корреляционной матрицы видно, что связи переменной х3со всеми остальными являются наиболее сильными (от 0,40 до 0,75), а корреляции переменной х2 — самыми слабыми (от 0,16 до 0,40).
Чаще всего в итоге факторного анализа определяется не один, а несколько факторов, по-разному объясняющих матрицу интеркорреляций переменных. В таком случае факторы делят на генеральные, общие и единичные.
Генеральными называются факторы, все факторные нагрузки которых значительно отличаются от нуля (нуль нагрузки свидетельствует о том, что данная переменная никак не связана с остальными и не оказывает на них никакого влияния в жизни).
Общие — это факторы, у которых часть факторных нагрузок отлична от нуля.
Единичные — это факторы, в которых существенно отличается от нуля только одна из нагрузок.
Вопросы для самопроверки:
-
Объясните значения фраз «высокая положительная корреляция» и «низкая отрицательная корреляция». Приведите примеры и графики, иллюстрирующие эти понятия. -
Сформулируйте в содержательных понятиях задачу из области специализации, при решении которой необходимо вычислять: коэффициент корреляции Пирсона, коэффициент корреляции Спирмена, коэффициент взаимной сопряженности. -
Перечислите причины появления ложной корреляции. -
Объясните смысл коэффициента ранговой корреляции? -
Может ли коэффициент корреляции быть равным нулю, когда между измеряемыми признаками наблюдается функциональная зависимость? -
Приведите примеры, когда нулевая корреляция предполагает независимость и когда нулевая корреляция такой зависимости не предполагает?
Регрессионный анализ
Довольно часто в практике исследовательской работы имеет место ситуация, когда важнейшие переменные, описывающие некоторый процесс, известны заранее, но модель процесса еще не известна. В этом случае возможны разные подходы. Одним из них является построение эмпирических моделей.
Построение эмпирических моделей предполагает проведение экспериментов или наблюдений для сбора опытных данных, выбор одной определенной модели из некоторого множества возможных, вычисление коэффициентов модели («подгонку») и оценку полученных результатов.
Число цветков при разном количестве неорганического брома в почве.
| Кол-во брома (мкг/см3) | 2 | 4 | 6 | 8 | 10 | 12 | 14 |
| Среднее число цветков | 3,6 | 2,9 | 3,2 | 1,8 | 2,3 | 1,7 | 0,8 |
Метод наименьших квадратов
Метод наименьших квадратов, разработанный знаменитыми математиками К. Гауссом и А. Лежандром, берет свое начало от задач геодезии и астрономии. Рассмотрим его существо на примере линейной модели. Итак, пусть для представления полученных данных мы выбрали линейную модель y
*=a+bx, где х – независимая переменная, т. е., переменная, которую экспериментатор может менять по своему усмотрению; y* - зависимая переменная или отклик; a и b – коэффициенты (параметры). Из данных, приведенных в примере, видно, что именно такой моделью (уравнением прямой линии) может быть описана зависимость.
С другой стороны, видно что реально наблюдаемые значения отклика yi несколько отличаются от откликов yi*, соответствующих уравнению модели. И такое положение будет всегда, даже в тех случаях, когда зависимая и независимая переменные будут связаны строгой функциональной зависимостью. В этом случае отклонения эмпирических значений от теоретических связаны с погрешностями измерений, которые всегда имеют место.
Итак, каждому значению независимой переменной в общем случае соответствует ошибка: i=yi-yi*.
Естественно, что в зависимости от того, как будет проведена прямая, аппроксимирующая набор экспериментальных данных, величины i будут различны. Именно, для того, чтобы избежать субъективности при построении эмпирической модели, и был разработан метод наименьших квадратов, позволяющий однозначно определить параметры выбранной модели. В основе этого метода лежит критерий минимизации суммы квадратов ошибок, т. е. требование, чтобы
была минимальной.Покажем, как используется метод наименьших квадратов на примере оценки параметров для уравнения y*=a+bx.
В общем случае необходимо решить систему уравнений:
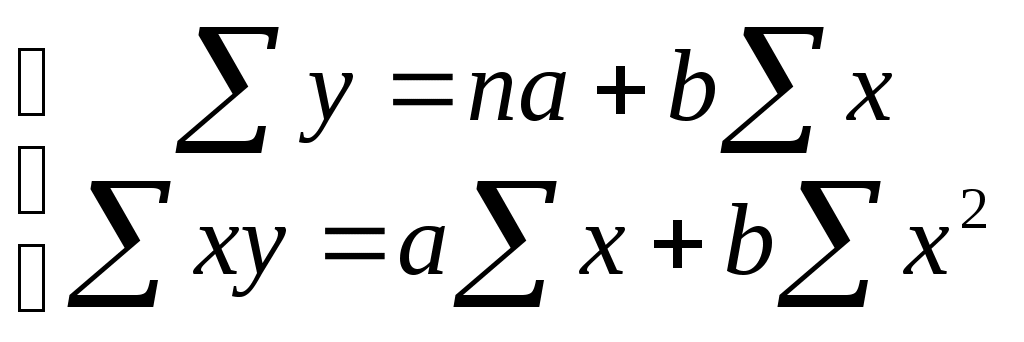, из которых находятся коэффициенты a и b.Подставляя данные из примера, получаем:
16,3=7a+56b
107=56a+560b
Откуда a=4, b=-0,209.
В таблице приведено сравнение между реальными и теоретическими данными, а также величины ошибок.
| Y | 3,6 | 2,9 | 3,2 | 1,8 | 2,3 | 1,7 | 0,8 |
| y* | 3,582 | 3,164 | 2,746 | 2,328 | 1,91 | 1,492 | 1,074 |
| i | 0,018 | -0,264 | 0,454 | -0,528 | 0,39 | 0,208 | -0,274 |
| Сумма i | 0,825 | | | | | | |
Выбор формы функциональной зависимости
Пусть имеется ряд данных, представляющих одну зависимую и одну независмую переменную, и требуется определить функциональную связь между ними. Универсального способа решения этой задачи не существует. Иногда анализ графического изображения имеющихся данных, а также понимание механизма исследуемого процесса помогают выбрать вид аналитической зависимости. Особенно просто оценить вид функциональной зависимости, если экспериментальные данные укладываются или группируются относительно некоторой прямой.
Значительное число зависимостей, встречающихся в практике научных исследований в самых разных областях знаний, может быть описано следующими уравнениями:
y=a+bx,
y=a+bx+cx2,
y=abx,
y=axb,
y=x/(a+bx).
Применение парного линейного уравнения регрессии
Прежде чем обсуждать вопросы использования уравнений парной регрессии, вспомним, что парный корреляционный анализ не дает чистых мер влияния только одного изучаемого фактора. Если факторы взаимосвязаны, то парная связь измеряет влияние данного фактора и часть влияния прочих факторов, связанных с ним.
Уравнение регрессии применимо для прогнозирования возможных ожидаемых значений результативного признака. При этом следует учесть, что перенос закономерности связи, измеренной в варьирующей совокупности, в статике на динамику, не является, строго говоря, корректным и требует условий допустимости такого переноса (экстраполяции), что выходит за рамки статистики и может быть сделано только специалистом, хорошо знающим объект (систему) и возможности его развития в будущем).
Ограничением прогнозирования на основе регрессионного уравнения, тем более парного, служит условие стабильности или по крайней мере малой изменчивости других факторов и условий изучаемого процесса, не связанных с ними. Если резко изменится внешняя среда протекающего процесса, прежнее уравнение результативного признака на факторный потеряет свое значение. В сильно засушливый год доза удобрения может не оказать влияния на урожайность, так как последнюю лимитирует пониженная влагообеспеченность (закон Либиха).
Корреляционно-регрессионные модели (КРМ)
и их применение в анализе и прогнозе.
Корреляционно-регрессионной моделью системы взаимосвязанных признаков является такое уравнение регрессии, которое включает основные факторы, влияющие на результативный признак, обладает высоким (не ниже 0.5) коэффициентом детерминации и коэффициентами регрессии.
Приведенное определение КРМ включает достаточно строгие условия: далеко не всякое уравнение регрессии можно считать моделью.
Теория и практика выработали ряд рекомендация для построения корреляционно-регрессионной модели:
-
Признаки-факторы должны находиться в причинной связи с результативным признаком (следствием). -
Признаки-факторы не должны быть составными частями результативного признака или его функциями. -
Признаки-факторы не должны дублировать друг друга, т.е. быть коллинеарными (с коэффициентом корреляции более 0.8). -
Не следует включать в модель факторы разных уровней иерархии, т.е. фактор ближнего порядка и его субфакторы. -
Желательно, чтобы между результативным признаком и факторами соблюдалось единство единиц совокупности, к которой они отнесены. -
Математическая форма уравнения регрессии должна соответствовать логике связи факторов с результатом в реальном объекте. Например, такие факторы как дозы различных удобрений, уровень плодородия, число прополок и т.п. создают прибавки величины урожайности мало зависящие друг от друга; урожайность может существовать и без любого из этих факторов. Такому характеру связи соответствует аддитивное уравнение регрессии: y=a+b1x1+b2x2+....bnxn -
Принцип простоты; предпочтительнее модели с меньшим числом факторов при том же коэффициенте детерминации или даже при существенно меньшем коэффициенте. -
Следует обращать внимание, что полученное уравнение регрессии не полностью описывает эмпирические данные и, в общем случае, Дисперсия (общая) = Дисперсия (объяснена уравнением регрессии) + Дисперсия (остаточная).
Интерпретировать корреляционные показатели строго следует лишь в терминах вариации (различий в пространстве) отклонений от средней величины. Если же задача исследования состоит в измерении связи не между вариацией двух признаков в совокупности, а между измерениями признаков объекта во времени, то метод корреляциооно-регрессионного анализа требует значительного изменения.
Из вышеприведенного определения об интерпретации показателей корреляции следует, что нельзя трактовать корреляцию признаков как связь их уровней. Это ясно хотя бы из такого примера: Если бы все студенты, которые ходят на лекции, учились бы только на пятерки, то вариация этого признака равнялась бы нулю, а следовательно успеваемость абсолютно не могла бы влиять на посещаемость. Параметры корреляции между успеваемостью и посещаемостью всегда будут равняться нулю. Но ведь и в этом случае уровень знаний зависел бы от числа лекций - он был бы тем выше, чем больше лекций.