ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 209
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Механическая система электропривода подъема
Проверка правильности выбора преобразователя
Исследование частoтно-регулируемого асинхронного электропривода крана со скалярном управлением
Разработка и исследование систем электропривода с векторным управлением
Финансовый менеджмент, ресурсоэффективность и ресурсосбережение
тока Тф.от
= 0.
Принимаем коэффициент аппроксимации звена чистого запаздывания апериодическим звеном:
nт 2 .
Эквивалентная малая постоянная времени оптимизированного контура тока
Т
Тос.т
n
тэ
т
4

2 10
4
Тзу.и Тф.от 2 2 10
0 3104 с.
Принимаем коэффициент типовой настройки контура тока на модульный
оптимум (МО):
ат 2 .
Постоянная времени регулятора тока:
Tрт Т1э 0,019315 с.
Коэффициент усиления регулятора тока:
k Т1э R1э

0,019315 0,082045
 3, 421
3, 421рт k k aТ
327,502 0,02357 2 3104
и т т
тэ .
т т μ тэ
Т aТ 2 3104 6 104 с.
Допустимое значение выходного сигнала регулятора тока
Nртdдоп 1
Допустимое значение выходного сигнала регулятора тока
I1d:
 I1q :
I1q : Nртqдоп
Nртqдоп 0
Параметры контура потокосцепления с ПИ-регулятором без датчика
Разрядность АЦП датчика потока
nацп. д
= 12.
Максимальное значение измеряемого потока
2изм.макс σ 2н 1,048 0,954 1 Вб ,
где σ 1,048 – коэффициент, учитывающий возможное увеличение потокосцепления за счет перерегулирования.
Коэффициент передачи датчика потока:
kд
0,5 2nацп.д
2изм.макс
0,5 212
1
2048 1 / Вб.
Принимаем:
Nо.макс 1.
Коэффициент обратной связи по потоку:
k
1
 2изм.макс
2изм.макс 1 11 / Вб.
 1
1Коэффициент согласования сигналов обратной связи и задания на входе контура потокосцепления:
kос.
1
 0,5 2nацп.д
0,5 2nацп.д 1
 0,5 212
0,5 212 4,883104
Коэффициент согласования сигналов обратной связи и задания на входе контура потокосцепления:
N 2н
k 0,954 0,954

з макс

2изм.макс
2н 1
Интервалы квантования сигналов в цепи обратной связи контура потока:
Тос.
Тпк.
10 Tшим
10 2 104 2 103 с.
Принимаем постоянную времени аналогового фильтра в цепи измерения
потока Тф.о
= 0.
Принимаем коэффициент аппроксимации звена чистого запаздывания апериодическим звеном:
n 1.
Эквивалентная малая постоянная времени оптимизированного контура потокосцепления:
Т Т 4 2 103
Тэ Tт ос.
n
-
Тф.о Tт ос.
n
Тф.о 6 10
0,0026 с.
 1
1Принимаем коэффициент типовой настройки контура потокосцепления на
модульный оптимум (МО):
а 2 .
Постоянная времени регулятора:
Тр T2 0,6176 с.
Коэффициент усиления регулятора:
 k Т2 kт
k Т2 kт 0,6176 0,02357
15,373
р L k aТ

0,018211 2 0,0026
m э
Допустимое значение выходного сигнала регулятора потока:
Nр доп Nзт. макс 0,667
Параметры контура скорости с ПИ-регулятором с импульсным датчиком скорости
Максимальное значение измеряемой скорости:
ωизм.макс σс ωэп.макс 1,29 77,456 100 рад / c,
где σс
-
коэффициент, учитывающий возможное увеличение скорости за
счет перерегулирования.
Принимаем
Nос.макс 1.
Коэффициент обратной связи по скорости:
k k 1 1 0,01 с / рад.
с ос.с
ωизм.макс 100
Значение максимального задания на входе контура скорости:
N ωэп.макс
77, 456 0,775
зс.макс
ωизм.макс 100
Интервалы квантования сигналов в цепи обратной связи контура скорости:
Т Т 10 T 10 2 104 2 103 с.
ос.с пк.с шим
Принимаем постоянную времени аналогового фильтра в цепи измерения
скорости
Тф.ос 0 .
Коэффициент аппроксимации звена чистого запаздывания апериодическим звеном:
nс 2.
Эквивалентная малая постоянная времени оптимизированного контура скорости:
n
сэ т ф.ос
T T Tос.с T 6 104
с
2 103

0 0,0016 с.
2
Принимаем коэффициенты типовой настройки контура скорости на
симметричный оптимум (СО) :
bc ac 2 .
Постоянная времени регулятора:
Трс bc acТсэ 2 2 0,0016 0,0064 с.
Коэффициент усиления регулятора:
k Jэ kт

3,521 0,02357
 47,639
47,639рс 3 Lm z
k a Т
0,954 3
0,01821
4 0,01 2 0,0016
2н 2
L2
р с c μсэ
2 0,0191454
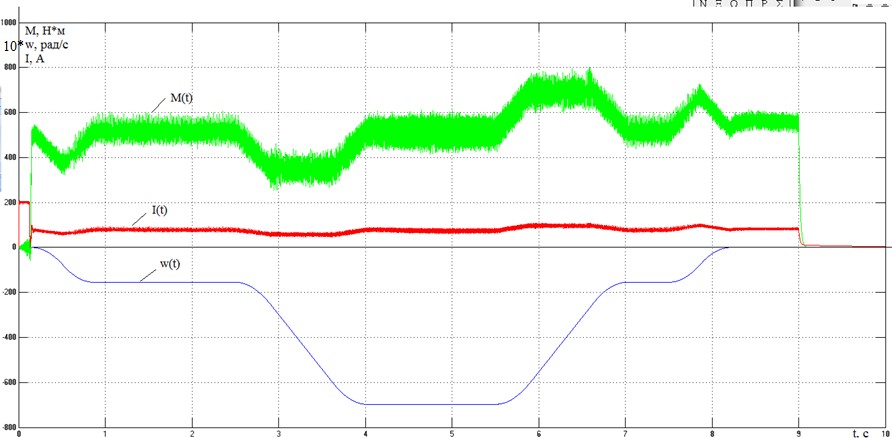
Рисунок 36 – Переходные процессы в электроприводе с векторным управлением при спуске краном груза массой 15 т.
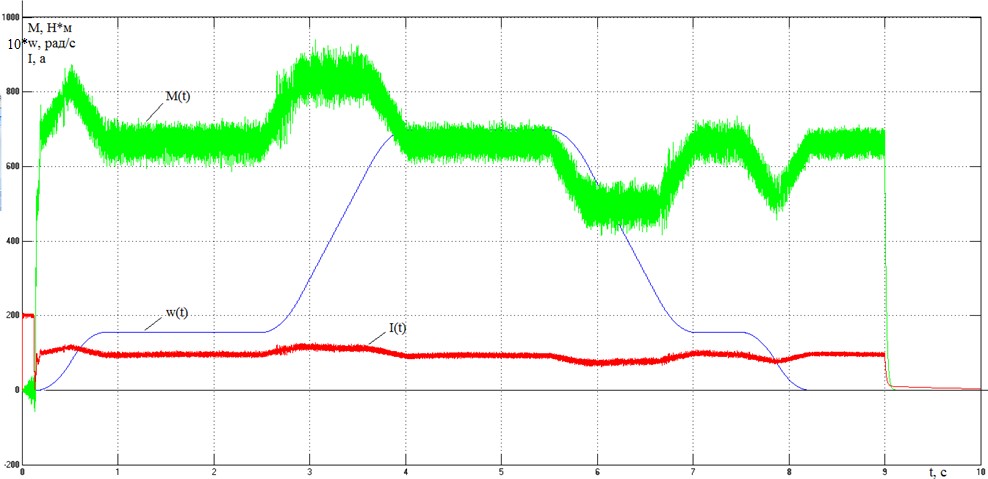
Рисунок 37– Переходные процессы в электроприводе с векторным управлением при подъеме краном груза массой 15 т.
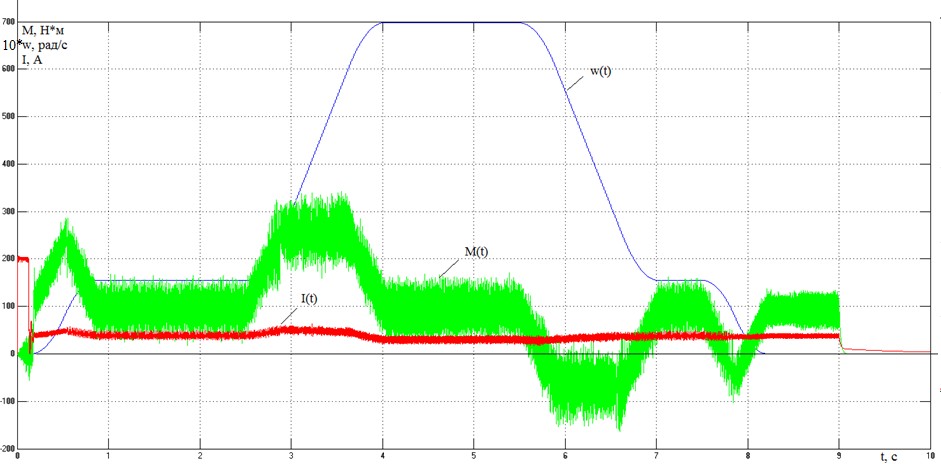
Рисунок 38– Переходные процессы в электроприводе с векторным управлением при подъеме краном пустого крюка
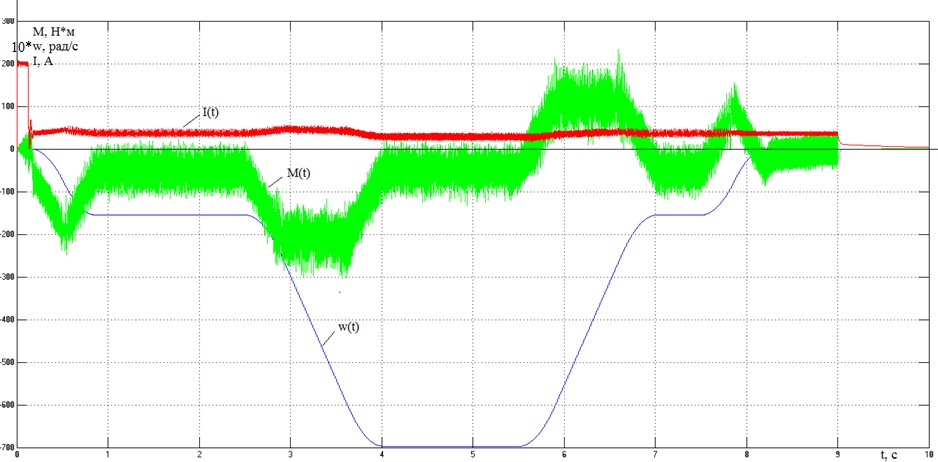
Рисунок 39– Переходные процессы в электроприводе с векторным управлением при спуске краном пустого крюка
Вывoд к разделу:
Преимущества векторного метода управления асинхронным двигателем:
-
Высокий уровень точности при регулировании скорости вращения вала, несмотря даже на возможное отсутствие датчика скорости; -
Осуществление вращения двигателя на малых частотах происходит без рывков, плавно; -
Установлен датчик скорости, с помощью его достигли номинального значения момента на валу даже при нулевом значении скорости; -
Быстрое реагирование на возможное изменение нагрузки – резкие скачки нагрузки практически не отражаются на скорости электропривода; -
Высокий уровень КПД двигателя, за счет сниженных потерь из-за намагничивания и нагрева.