ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 90
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| 1 | 4 | 6 |
| 0,1 | 0,6 | 0,3 |
Найти ее математическое ожидание.
-
Согласно статистике, вероятность того, что двадцатипятилетний человек проживет еще год, равно 0,992. Компания предлагает застраховать жизнь на год на 1000 у.е. с уплатой 10 у.е. взноса. Определить, какую прибыль ожидает компания от страховки одного двадцатипятилетнего человека. -
Случайная величина Х задана законом распределения:
| 1 | 5 | 8 |
| 0,1 | 0,2 | 0,7 |
Найти дисперсию и среднее квадратичное отклонение этой случайной величины Х.
-
Случайные величины X и Y заданы законом распределения. Найти математическое ожидание этих случайных величин и определить по таблицам, какая из данных величин более рассеяна. Подсчитать дисперсии D(X) и D(Y). Убедиться, что D(X)>D(Y).
| X | 2 | 20 | 28 | 50 |
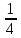 | 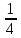 | 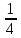 | 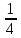 |
| Y | 23 | 25 | 26 |
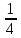 | 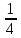 | 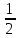 |
6.9.2. Время на выполнение: 45 мин.
6.9.3. Перечень объектов контроля и оценки
| Наименование объектов контроля и оценки | Основные показатели оценки результата | Оценка |
| У5. Умение решать задачи на вычисление вероятности с использованием элементов комбинаторики | Нахождение вероятности случайного события. Составление закона распределения случайной величины. Вычисление числовых характеристик случайных величин. Формулировка классического определения вероятности. | 11 баллов |
За правильный ответ на вопросы или верное решение задачи выставляется положительная оценка – 1 балл.
За неправильный ответ на вопросы или неверное решение задачи выставляется отрицательная оценка – 0 баллов.
6.10. Расчетное задание
6.10.1. Текст задания
Задание 1: 1) Найти множества А∩В, АUВ, А/В, В/А, если:
а) А={е, о, р, х} В={х, у}
б) А={х: -3<х<4} В={х: 0≤х≤6}
в) А={2n+1}, B={n+1} nєN
2) Найти множества А∩В, АUВ, А/В, В/А, если:
а) А={12, 13, 14, 15} В={12, 14, 16}
б) А={х: 0<х<2} В={х: 1≤х≤4}
в) А={3-(n+1)}, B={n+5} nєN
Задание 2: 1) На 1 курсе учатся 200 студентов, 106 из них знают английский язык, 60 – немецкий, 92 – французский. 24 студента знают английский и немецкий языки, 36 – английский и французский, 30 – немецкий и французский, 14 – все три языка. Остальные знают только один испанский язык. Сколько студентов знают:
а) только один язык?
б) испанский язык?
в) только немецкий язык?
г) знают английский и немецкий, но не знают французский?
2) На 1 курсе учатся 200 студентов, 106 из них знают английский язык, 60 – немецкий, 92 – французский. 24 студента знают английский и немецкий языки, 36 – английский и французский, 30 – немецкий и французский, 14 – все три языка. Остальные знают только один испанский язык. Сколько студентов знают:
а) ровно два языка?
б) только французский язык?
в) знают немецкий и французский, но не знают английский?
г) не знают испанский язык?
6.10.2. Время на выполнение: 45 мин.
6.10.3. Перечень объектов контроля и оценки
| Наименование объектов контроля и оценки | Основные показатели оценки результата | Оценка |
| У 3. Уметь вычислять значения геометрических величин | Формулировка основных понятий дискретной математики и теории множеств | 32 балла |
За правильный ответ на вопросы или верное решение задачи выставляется положительная оценка – 1 балл.
За неправильный ответ на вопросы или неверное решение задачи выставляется отрицательная оценка – 0 баллов.
6.11. Устный ответ
6.11.1. Текст задания
Тема 3.1. Множества и отношения.
Тема 3.2. Основные понятия теории графов.
-
Кто является основоположником теории множеств? -
Какие два множества являются равными? -
Как называется множество, в котором нет ни одного элемента? -
Составьте множество и запишите два элемента принадлежащие этому множеству и два элемента не принадлежащие ему. -
Какое множество является подмножеством данного множества? -
Для множества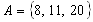 составьте все его подмножества.
составьте все его подмножества. -
Какое множество является пересечением двух множеств? Приведите пример. -
Какое множество является объединением двух множеств? Приведите пример. -
Как вычитаются множества? Приведите пример. -
Что называется графом? -
Какой граф называется ориентированным? -
Что называют степенью вершины? -
Что называют маршрутом в графе? Виды маршрутов. -
Что называется циклом? Виды циклов.
6.11.2. Время на выполнение: 25 мин.
6.11.3. Перечень объектов контроля и оценки
| Наименование объектов контроля и оценки | Основные показатели оценки результата | Оценка |
| З4. Знание роли и места математики в современном мире при освоении профессиональных дисциплин и в сфере профессиональной деятельности | Формулировка основных понятий дискретной математики и теории множеств | 14 баллов |
За правильный ответ на вопросы или верное решение задачи выставляется положительная оценка – 1 балл.
За неправильный ответ на вопросы или неверное решение задачи выставляется отрицательная оценка – 0 баллов.
6.12. Расчетное задание
6.12.1. Текст задания
Задание 1. Вычислить, выписать вещественную и мнимую части полученных комплексных чисел.
1)
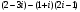 2)
2) 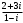 3)
3) 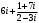
4)
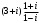 5)
5) 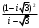 6)
6) 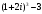
7)
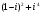
Задание 2. Запишите предложенные комплексные числа в тригонометрической форме:
1)
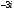 ; 2)
; 2) 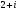 ; 3)
; 3) 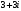 ; 4)
; 4) 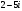 5)
5) 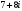 6)
6) 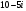 7)
7) 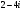 .
.Задание 3. Найти все корни уравнений:
1)
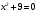 ; 2)
; 2) 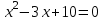 ; 4)
; 4) 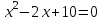 ; 5)
; 5) 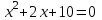 ; 6)
; 6) 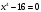 7)
7) 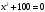
Задание 4. Комплексное число имеет вид:
1)
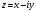 ; 2)
; 2) 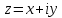 3)
3) 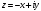 4)
4) 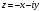
Задание 5. Тригонометрическая форма комплексного числа имеет вид:
-
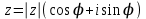 2)
2) 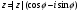
3)
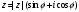 4)
4) 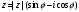
Задание 6. Назовите действительную часть комплексного числа
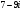 :
:-
9 2)-9 3)-7 4)7
Задание 7. Назовите мнимую часть комплексного числа
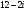 :
:
-
12 2)-12 3)-2 4)2
Задание 8. Решением уравнения
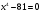 являются числа:
являются числа:1)3,-3,3i,-3i 2)3,-3 3) 3i,-3i 4)3, 3i,-3i
Задание 9. Суммой комплексных чисел
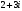 и
и 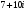 является число:
является число:1)9+13i 2)9+3i 3)2+13i 4)9+10i
Задание 10. Разностью комплексных чисел
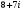 и
и 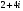 является число:
является число:1)6+3i 2)10+11i 3)6+11i 4)6-3i
Задание 11. Произведением комплексных чисел
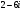 и
и 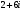 является число:
является число: -
40 2)-32 3)4-36i 4)4+36i
Задание 12. Найти модуль комплексного числа
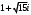 :
:-
4 2) 16 3)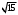 4)
4) 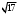
Задание 13. Аргументом комплексного числа является
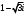 :
:-
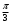 2)
2) 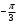 3)
3) 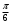 4)
4) 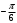
6.12.2. Время на выполнение: 135 мин.
6.12.3. Перечень объектов контроля и оценки
| Наименование объектов контроля и оценки | Основные показатели оценки результата | Оценка |
| У 2. Умение выполнять действия над комплексными числами | Выполнение действий над комплексными числами Нахождение аргумента и модуля комплексного числа Формулировка определений и перечисление свойств комплексных чисел | 21 балл |
За правильный ответ на вопросы или верное решение задачи выставляется положительная оценка – 1 балл.
За неправильный ответ на вопросы или неверное решение задачи выставляется отрицательная оценка – 0 баллов.