ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 91
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
6.13.Устный ответ
6.13.1. Текст задания
1. Какие числа называются комплексными и мнимыми?
2. Как геометрически представляется комплексное число?
3. Что называется модулем комплексного числа?
-
4. Как выполняется сложение и вычитание комплексных чисел?
5. Как геометрически представляется сумма двух комплексных чисел?
6. Как выполняется умножение комплексных чисел?
7. Как выполняется деление комплексных чисел?
8. Как выполняется возведение в степень мнимых и комплексных чисел?
6.13.2. Время на выполнение: 8 мин.
6.13.3. Перечень объектов контроля и оценки
| Наименование объектов контроля и оценки | Основные показатели оценки результата | Оценка |
| З2. Знание основных понятий и методов математического анализа, линейной алгебры, теории комплексных чисел, теории вероятностей и математической статистики | Формулировка определений и перечисление свойств комплексных чисел | 8 баллов |
За правильный ответ на вопросы или верное решение задачи выставляется положительная оценка – 1 балл.
За неправильный ответ на вопросы или неверное решение задачи выставляется отрицательная оценка – 0 баллов.
6.14. Устный ответ
Тема 5.1. Вероятность. Теоремы сложения вероятностей
Тема 5.2. Случайная величина, ее функция распределения.
Тема 5.3. Математическое ожидание и дисперсия случайной величины.
6.14.1. Текст задания
-
Что называется n –факториалом? -
Перечислите основные задачи комбинаторики. -
Что называется перестановками? -
Запишите формулу для числа перестановок из m элементов. -
Что называется размещением? -
Запишите формулу числа перестановок из m элементов по n. -
Что называется сочетанием? -
Запишите формулу для числа сочетаний из m элементов по n. -
Какие события называются достоверными? Приведите примеры. -
Какие события называются невозможными? Приведите примеры. -
Что называется вероятностью события? -
Какие события называются несовместными? Приведите примеры. -
Какие события называются противоположными? Приведите примеры. -
Что называется условной вероятностью? -
Как формулируется теорема сложения вероятностей? -
Чему равна сумма вероятностей противоположных событий? -
Как формулируется теорема умножения вероятностей? -
Какая величина называется случайной? -
Какая случайная величина называется дискретной? -
Опишите схему Бернулли. Какие элементарные события повторяются в этих опытах? -
Запишите формулу Бернулли. -
Что называется законом распределения случайной величины? -
Какой закон распределения называется биноминальным? -
Что называется математическим ожиданием дискретной случайной величиной? -
Что называется дисперсией случайной величины? -
Что понимается под законом больших чисел?
6.14.2. Время на выполнение: 60 мин.
6.14.3. Перечень объектов контроля и оценки
| Наименование объектов контроля и оценки | Основные показатели оценки результата | Оценка |
| З2. Знание основных понятий и методов математического анализа, линейной алгебры, теории комплексных чисел, теории вероятностей и математической статистики | Формулировка определений и перечисление свойств основ теории вероятностей и математической статистики | 26 баллов |
За правильный ответ на вопросы или верное решение задачи выставляется положительная оценка – 1 балл.
За неправильный ответ на вопросы или неверное решение задачи выставляется отрицательная оценка – 0 баллов.
6.15. Расчетное задание
6.15.1. Текст задания
Задание: 1. Решить комбинаторную задачу.
2. Найти вероятность события.
| Вариант | Задание 1. | Задание 2. |
| 1. | 1. Сколько различных перестановок можно сделать из букв слова «МАТЕМАТИКА»? 2. Сколькими способами из группы в 20 человек можно составить команду из трёх человек? 3. Сколькими способами можно выбрать двух человек из 12, если один из них должен быть старше? | 1. В ящике 18 чёрных, 3 синих, 2 красных. Вынули один шар. Найти вероятность того, что вынули чёрный или красный шар. 2. В группе 15 юношей и 13 девушек. Выбираем двух человек. Какова вероятность того, что выберут юношу и девушку. |
| 2. | 1. Сколько трёхзначных чисел можно составить из простых чисел, если каждая из этих цифр может повторяться? 2. Из восьми намеченных кандидатов нужно выбрать трёх тренеров одинаковой специализации. Сколькими способами можно это сделать? 3. Есть книги 8 видов. Сколькими способами можно составить наборы из четырёх книг? | 1. В группе 4 юноши и 16 девушек. Выбираем двух человек. Какова вероятность того, что выберут юношу или девушку? 2. В ящике 6 чёрных и 3 красных шара. Если первый раз вынули красный шар, то предоставляется право вынуть ещё раз шар. Какова вероятность того, что оба раза вынули красный шар? |
| 3. | 1. Сколько различных двухзначных чисел можно образовать из цифр 1, 3, 4, 5 при условии, что в каждом числе нет одинаковых цифр? 2. Сколько различных комбинаций по семь букв можно составит из элементов O O N S N O S? 3. Сколькими способами можно выбрать трёх нападающих из 10? | 1. Есть 100 жетонов от 1 до 100. Какова вероятность того, что номер наудачу взятого жетона кратен 30 или 13? 2. В ящике 12 деталей стандартных и 8 нестандартных. Вынули поочерёдно четыре детали. Какова вероятность того, что все четыре детали стандартные? |
| 4. | 1. Сколько трёхзначных чисел можно составить из цифр 2, 5, 9, если каждая цифра входит в изображение числа только один раз? 2. Сколько можно составить сигналов из 6 флажков различного цвета, взятых по два? 3. Сколькими способами можно составить наборы Новогодних открыток, если их имеется в наличии 9 видов? (открытки в наборе могут повторяться). | 1. . В ящике 10 чёрных, 7 синих, 13 красных. Вынули один шар. Найти вероятность того, что вынули синий или красный шар. 2. В ящике 12 деталей стандартных и 8 нестандартных. Вынули поочерёдно четыре детали. Какова вероятность того, что все четыре детали нестандартные? |
| 5. | 1. Сколькими способами можно выбрать две точки из семи точек на прямой? 2. Сколько «слов», каждое из которых состоит из пяти различных букв можно составить из букв слова ОБРАЗ? 3. Сколькими способами можно выбрать 6 книг по информатике из 8? | 1. Из колоды, содержащей 36 карт, наудачу извлекается одна карта. Какова вероятность того, что вынута карта дама или карта пиковой масти? 2. В ящике 12 белых и 6 чёрных шаров. Вынули поочерёдно три шара. Какова вероятность того, что все три шара чёрные? |
| 6. | 1. Сколько различных перестановок можно сделать из букв слова «МАТЕМАТИКА»? 2. Сколькими способами из группы в 20 человек можно составить команду из трёх человек? 3. Сколькими способами можно выбрать двух человек из 12,если один из них должен быть старше? | 1. Вероятность попадания игрока №1 в мишень равна 0.9, а игрока №2-0.4 . Какова вероятность того, что хотя бы один из игроков поразит цель, если они стреляют независимо друг от друга. 2. В первом ящике 1 белый, 2 красных и 3 синих шара, во втором ящике 2 белых, 6 красных и 4 синих шара. Из каждого ящика вынули по одному шару. Какова вероятность того, что среди вынутых шаров оба сини. |
| 7. | 1. Сколько трёхзначных чисел можно составить из простых чисел, если каждая из этих цифр может повторяться? 2. Из восьми намеченных кандидатов нужно выбрать трёх тренеров одинаковой специализации. Сколькими способами можно это сделать? 3. Сколькими способами можно распределить пять должностей между пятью лицами, избранными в президиум спортивного общества? | 1. Есть 100 жетонов от 1 до 100. Какова вероятность того, что номер наудачу взятого жетона кратен 11 или 13? 2. В первом ящике 3 белых и 5 синих шаров; во втором ящике 4 белых, 3 синих и 1 чёрный. Из каждого ящика наудачу вынули по одному шару. Какова вероятность того, что оба шара белые? |
| 8. | 1. Сколько различных двухзначных чисел можно образовать из цифр 1, 3, 4, 5 при условии, что в каждом числе нет одинаковых цифр? 2. Сколько различных комбинаций по семь букв можно составить из элементов O O N S N O S? 3. В бригаде из 25 человек надо выделить четырёх человек для работы в саду. Сколькими способами это можно сделать? | 1. В ящике 15 ч1рных, 4 синих, 25 красных. Вынули один шар. Найти вероятность того, что вынули чёрный или красный шар. 2. В группе 12 юношей и 18 девушек. Выбираем двух человек. Какова вероятность того, что выбрали юношу и девушку. |
| 9. | 1. Сколько трёхзначных чисел можно составить из цифр 2, 5, 9, если каждая цифра входит в изображение числа только один раз? 2. Сколько можно составить сигналов из 6 флажков различного цвета, взятых по два? 3. Есть книги 6 видов. Сколькими способами можно составить наборы по 5 книг? | 1. В партии из 30 пар обуви имеется 10 пар мужской, 8 пар женской и 12 пар детской обуви. Найти вероятность того, что взятая наудачу пара обуви будет женской или детской. 2. В ящике 9 белых и 1 чёрный шар. Вынули поочерёдно три шара. Какова вероятность того, что все три шара белые? |
| 10. | 1. Сколькими способами можно выбрать две точки из семи точек на прямой? 2. Сколько «слов», каждое из которых состоит из пяти различных букв можно составить из букв слова ОБРАЗ? 3. Сколько двухзначных чисел можно составить из цифр 2,5,8, если цифры могут повторяться? | 1. В партии из 30 пар обуви имеется 10 пар мужской, 8 пар женской и 12 пар детской обуви. Найти вероятность того, что взятая наудачу пара обуви будет не женской. 2. В ящике 8 белых, 3 чёрных и 5 жёлтых шаров. Вынули поочерёдно три шара. Какова вероятность того, что все три шара жёлтые? |
6.15.2. Время на выполнение: 60 мин.
6.15.3. Перечень объектов контроля и оценки
| Наименование объектов контроля и оценки | Основные показатели оценки результата | Оценка |
| З2. Знание основных понятий и методов математического анализа, линейной алгебры, теории комплексных чисел, теории вероятностей и математической статистики | Знание методов и формул для решения комбинаторных задачи и нахождения вероятности события. | 5 баллов |
За правильный ответ на вопросы или верное решение задачи выставляется положительная оценка – 1 балл.
За неправильный ответ на вопросы или неверное решение задачи выставляется отрицательная оценка – 0 баллов.
7. Задания промежуточной аттестации.
К сдаче экзамена допускаются студенты, сдавшие на положительную оценку, все практические работы по изучаемой дисциплине.
7.1.Экзаменационные вопросы для студентов.
-
Матрицы, действия над матрицами. -
Определители 1-го, 2-го, 3-го порядков. Правило треугольников. -
Определители n-го порядка. Теорема Лапласа. -
Обратная матрица. Алгоритм нахождения обратной матрицы. -
Ранг матрицы. Алгоритм вычисления ранга матрицы с помощью элементарных преобразований. -
Система линейных уравнений. Метод обратной матрицы. Формулы Крамера. Метод Гаусса. -
Предел функции в точке. Основные теоремы о пределах. -
Предел функции при x, стремящемся к бесконечности. Замечательные пределы. Число е. -
Непрерывность функции в точке и на промежутке. Точка непрерывности функции. Точка разрыва функции. Свойства непрерывных функций. Приращение аргумента. Приращение функции. -
Производная функции. Дифференциал функции. Геометрический смысл производной. Механический смысл производной. -
Таблица производных. Понятие сложной функции. Производная сложной функции. -
Схема исследования функции. Область определения функции. Множество значений функции. Четность и нечетность функции. Нули функции. Промежутки знакопостоянства функции. Возрастание и убывание функции, правило нахождения промежутков монотонности. Точки экстремума функции, правило нахождения экстремумов функции. -
Производные высших порядков. Физический смысл второй производной. Исследование функции с помощью второй производной. -
Первообразная. Неопределенный интеграл. Основные свойства неопределенного интеграла. -
Таблица неопределенных интегралов. -
Методы интегрирования: метод непосредственного интегрирования; метод замены переменной (метод подстановки); метод интегрирования по частям. -
Определенный интеграл. Понятие интегральной суммы. Достаточное условие существования определенного интеграла (интегрируемости функции). -
Основные свойства определенного интеграла. Геометрический смысл определенного интеграла. -
Методы вычисления определенных интегралов. Формула Ньютона-Лейбница. -
Геометрические и физические приложения определенного интеграла. -
Функции нескольких переменных. Частные производные. -
Понятие события. Достоверные, невозможные, совместные, несовместные, противоположные события. Классическое определение вероятности. -
Теорема сложения вероятностей. Теорема умножения вероятностей. -
Случайная величина. Дискретная и непрерывная случайные величины. Закон распределения дискретной случайной величины. Интегральная функция распределения непрерывной случайной величины. -
Математическое ожидание дискретной случайной величины. Отклонение случайной величины. Дисперсия дискретной случайной величины. Среднее квадратичное отклонение случайной величины.
7.2. Экзаменационные задания
-
Вычислить предел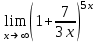 .
. -
Вычислить пределы:
а)
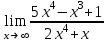 ; б)
; б) 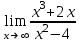 ; в)
; в) 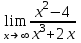 .
.-
Вычислить предел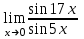 .
. -
Вычислить предел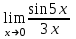 .
. -
Вычислить предел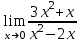 .
. -
Вычислить предел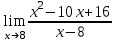 .
. -
Исследовать функцию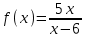 на непрерывность в точке
на непрерывность в точке 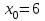 .
. -
Исследовать функцию и построить ее график.
и построить ее график. -
Вычислить значение производной следующих функций в точке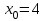 :
:
а)
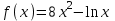 ; б)
; б) 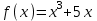 .
.-
Найти производную функции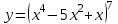 .
. -
Найти производную функции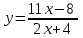 .
. -
Найти производную функции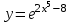 .
. -
Найти производную функции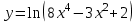 .
. -
Найти неопределенный интеграл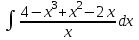 .
. -
Найти неопределенный интеграл методом замены переменной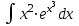 .
. -
Найти неопределенный интеграл методом замены переменной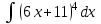 .
. -
Найти неопределенный интеграл методом замены переменной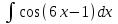 .
. -
Найти неопределенный интеграл методом замены переменной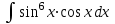 .
. -
Вычислить определенный интеграл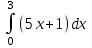 .
. -
Вычислить определенный интеграл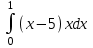 .
. -
Вычислить определенный интеграл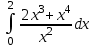 .
. -
Скорость движения точки изменяется по закону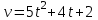 (м/с). Найти путь s, пройденный точкой за 4 с от начала движения.
(м/с). Найти путь s, пройденный точкой за 4 с от начала движения. -
Вычислить объем тела, полученного от вращения фигуры, ограниченной линиями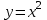 ,
, 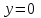 ,
, 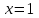 ,
, 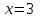 , вокруг оси Ox.
, вокруг оси Ox. -
Вычислить площадь фигуры, ограниченной линиями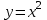 ,
, 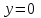 ,
, 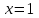 ,
, 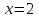 .
. -
В одной корзине находятся 5 белых и 10 черных шаров, в другой – 4 белых и 11 черных. Из каждой корзины вынули по шару. Найти вероятность того, что оба шара окажутся черными. -
В лотерее 1000 билетов. Разыгрывается один выигрыш в 200 рублей и десять выигрышей по 100 рублей. Пусть Х – величина возможного выигрыша для человека, имеющего один билет. Составить закон распределения этой случайной величины Х. -
Случайная величина Х задана законом распределения: