Поскольку исходная система уравнений являлась замкнутой (четыре уравнения и четыре неизвестных – , , , ), то появление дополнительных членов в уравнениях Рейнольдса приводит к тому, что она превращается в незамкнутую. Возникает новая проблема «замыкания системы уравнений Рейнольдса».
2.3.3 Полуэмпирические теории турбулентности

Современная теория турбулентности не располагает возможностями теоретическим путем получить уравнения для определения напряжений Рейнольдса. Поэтому единственным способом, позволяющим замкнуть систему, является привлечение полуэмпирических соотношений, связывающих эти напряжения с осредненными по времени компонентами скорости , и .

Один из первых исследователей турбулентности, Ж. Буссинеск, предложил выражать турбулентные напряжения аналогично закону трения Ньютона, т.е.

, (2.35)

гдеh-турбулентная вязкость.

В отличие от физической, турбулентная вязкость характеризует не физические свойства жидкости, а статистические свойства пульсационного движения. Поэтому она не является постоянной величиной, а может изменяться как в пространстве, так и во времени. Важно также отметить, что даже на небольших удалениях от твердых границ турбулентная вязкость существенно превосходит физическую ( ).

В целом для турбулентного потока можно записать

. (2.36)

Однако представление Буссинеска не приводит к решению задачи, т.к., к сожалению, отсутствуют прямые методы определения турбулентной вязкости.

Первого заметного успеха в этом направлении добился Л. Прандтль в 1925 году, предложив так называемую теорию пути перемешивания (смешения).

---

В основе ее лежит аналогия с кинетической теорией газов и предположение о том, что путь смешения зависит от условий течения. В соответствии с гипотезой Прандтля, каждый турбулентный моль (вихрь) жидкости переносит некоторое количество движения, которое сохраняется постоянным на пути перемешивания. Другими словами, длина пути перемешивания в известной мере аналогична длине свободного пробега молекул в кинетической теории газов, и определяет путь, который проходит моль жидкости, прежде чем он перемешается с другими жидкими образованиями и передаст свой импульс.

Допустив далее, что вертикальная и горизонтальная компоненты пульсационной скорости ( и ) являются величинами одного порядка, Прандтль получил формулу для определения турбулентного напряжения в виде

, (2.37)

где – длина пути перемешивания.

Угловые скобки вокруг u, символизирующие операцию осреднения, для упрощения записи опущены.

Вывод формулы Прандтля рассматривается в [6,7] На первый взгляд может показаться, что формула Прандтля не имеет каких-либо существенных преимуществ по сравнению с формулой Буссинеска, и единственным результатом является замена одной не поддающейся вычислению величины другой – . Однако это не так, поскольку величину оценить значительно проще, чем . В частности, не может быть больше размера канала и должна стремиться к нулю вблизи твердой стенки (поперечное движение у стенки невозможно).
2.3.4 Турбулентное течение в трубах

Расчет турбулентного течения в трубах относится к широко распространенным инженерным задачам. Одним из важных элементов расчета является нахождение закона распределения осредненных скоростей в поперечном сечении трубы.

---

По Прандтлю, поток в трубах при турбулентном течении условно разбивается на две области (двухслойная модель Прандтля): турбулентное ядро, в котором определяющими являются напряжения Рейнольдса, и тонкий вязкий подслой (ламинарный подслой по Прандтлю либо пристенный слой) вблизи стенки, в котором влияние турбулентности пренебрежимо мало, а касательные напряжения обусловлены физической вязкостью в соответствии с законом трения Ньютона.

На рисунке 1.4 приведен примерный вид поля осредненных скоростей (эпюра скорости) при турбулентном течении в трубопроводе. Следует обратить внимание на ее большую наполненность (большую равномерность) по сравнению с ламинарным течением. Это объясняется тем, что вследствие перемешивания частиц за счет турбулентных пульсаций происходит обмен количеством движения и, как следствие, более равномерное распределение скоростей в поперечном сечении.



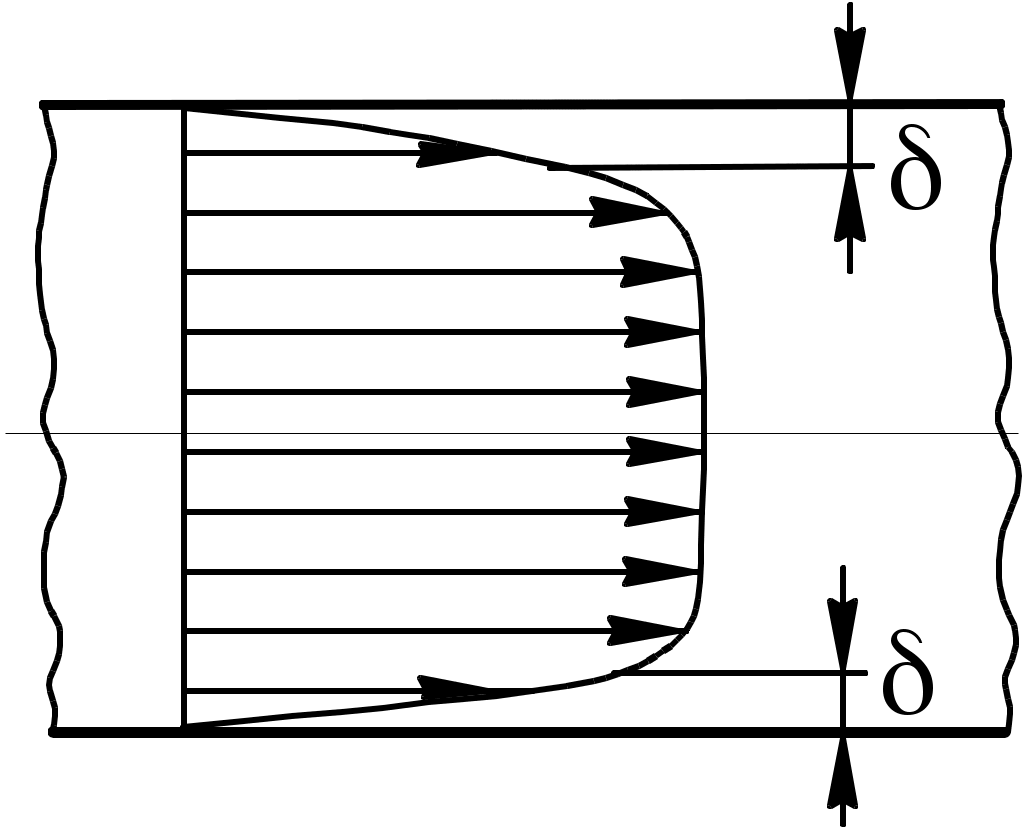
Рисунок 1.4 – Эпюра скорости

В непосредственной близости от стенки в пределах пристенного слоя решающее влияние на течение оказывают жесткость стенки, ее непроницаемость и эффект прилипания частиц. На самой стенке справедливы условия: ; ; .

Таким образом, для области в пределах вязкого подслоя можно записать:

. (2.38)

где – касательное напряжение на стенке.

Интегрирование (2.38) дает

. (2.39)

при , и . Таким образом,

. (2.40)

Имея в виду, что , после подстановки получаем:

---

. (2.41)

Из чего следует, что в пределах подслоя скорость изменяется по линейному закону. Величина имеет размерность квадрата скорости, поэтому корень квадратный из нее, т.е.

(2.42)

называют динамической скоростью либо скоростью трения. Из выражения для напряжений Рейнольдса (2.34) следует, что и

. (2.43)

Таким образом, динамическая скорость является мерой интенсивности турбулентного пульсационного движения, т.е. мерой интенсивности переноса количества движения.

Подставляя (2.42) в (2.41), получаем

. (2.44)

Оценим толщину вязкого подслоя. На его границе , и (2.44) можно придать вид

. (2.45)

В правой части стоит выражение, аналогичное числу Рейнольдса. Согласно тщательным опытам ближайшего сотрудника Л. Прандтля, Никурадзе, эта величина приближенно равна 11,6; тогда

. (2.46)

Очевидно, что этим соотношением можно воспользоваться лишь в случае, если известна динамическая скорость. Для ее нахождения необходимо увязать ее с параметрами осредненного потока, что является решаемой задачей.

Чтобы завершить вопрос о турбулентном течении в трубах, установим закон распределения осредненных скоростей в ядре потока. В этой области определяющую роль играют турбулентные касательные напряжения, и, следовательно, можно воспользоваться формулой Прандтля (2.37). Однако для того, чтобы продвинуться дальше, необходимо принять дополнительные допущения. Они оказываются достаточно грубыми, и единственным их оправданием является то, что результаты, к которым они приводят, достаточно хорошо согласуются с экспериментальными данными.

Первое допущение связано с длиной пути перемешивания. Согласно наиболее простой гипотезе, принадлежащей Л. Прандтлю,

, (2.47)

где

---

– величина, называемая постоянной Кармана. Выполненные измерения показывают, что . Более поздние исследования показали, что зависимость (2.47) справедлива лишь в пристенной части турбулентного ядра потока.

Вторым является допущение о касательных напряжениях. Следует полагать, что принципиально они являются величинами переменными. Однако, если рассматривать область, расположенную достаточно близко к стенке, то здесь величина касательного напряжения изменяется незначительно, и можно принять ее равной касательному напряжению на стенке, т.е. .

При этих допущениях формула Прандтля принимает вид

, (2.48)

либо

. (2.49)

Извлекая квадратный корень и разделяя переменные, получаем

(2.50)

и после интегрирования

. (2.51)

т.е. скорости в ядре потока распределены по логарифмическому закону.

Произвольную постоянную интегрирования можно найти из граничных условий на оси трубы: при , , и . После подстановки и простых преобразований получим

. (2.52)

Строго говоря, соотношение (2.52) выводится для плоских труб, но опыт показывает, что оно оказывается справедливым и для круглых, и подтверждает экспериментально установленный факт о независимости распределения скорости от причин, обусловливающих возникновение касательных напряжений (вязкости, шероховатости).

Выражение (2.52) иногда называют законом дефекта скорости.

Использование двухслойной модели, т.е. разделение потока на ядро и пристенный слой, приводит к специфической классификации стенок труб. Если толщина пристенного слоя больше выступов шероховатости, трубы называют гидравлически гладкими, в противном случае – шероховатыми.

---

Смотрите также файлы

• Темы занятий.docx

• Химический факультет отчет по учебной практике.docx

• Разговор о важном 23 января 2023 г.docx

• Тема вкр Моделирование специальной физической подготовки в тренировочном процессе биатлонистов оглавление.docx

• Бортовые магнитофоны.pptx