Стоит уделить внимание следующим обстоятельствам. Как отмечалось, для получения закона распределения скоростей в поперечном сечении трубопровода использовались простейшие гипотезы: постоянство касательных напряжений в ядре потока ( ) и линейная зависимость для длины пути перемешивания ( ). Легко показать, что первая из них не согласуется с реальностью при рассмотрении течения в трубах. Действительно, выделим в трубе цилиндрический элемент жидкости длиной l и радиусом r, на который действует постоянный перепад давления . Сила давления на этот элемент , а сила трения . Приравняв эти силы, получаем

. (2.53)

А для всей трубы длиной l и радиусом R

, (2.54)

где – напряжение на стенке.

Поскольку по условию, то приравняв (2.53) и (2.54), с учетом того, что ,

, (2.55)

т.е. касательные напряжения по сечению не постоянны, а изменяются по линейному закону, и лишь на достаточно малом расстоянии от стенки ( ) можно считать, что .

Вторая гипотеза также не согласуется с данными опытов. На рисунке 1.5 приведены графики, характеризующие распределение длины пути перемешивания в поперечном сечении круглой трубы по данным опытов Никурадзе (кружки) и по формулам, предложенным различными авторами. В соответствии с результатами экспериментов, значение

---

достигает максимума на оси трубы. Из графика следует, что гипотеза Прандтля (прямая 1) неприемлема.



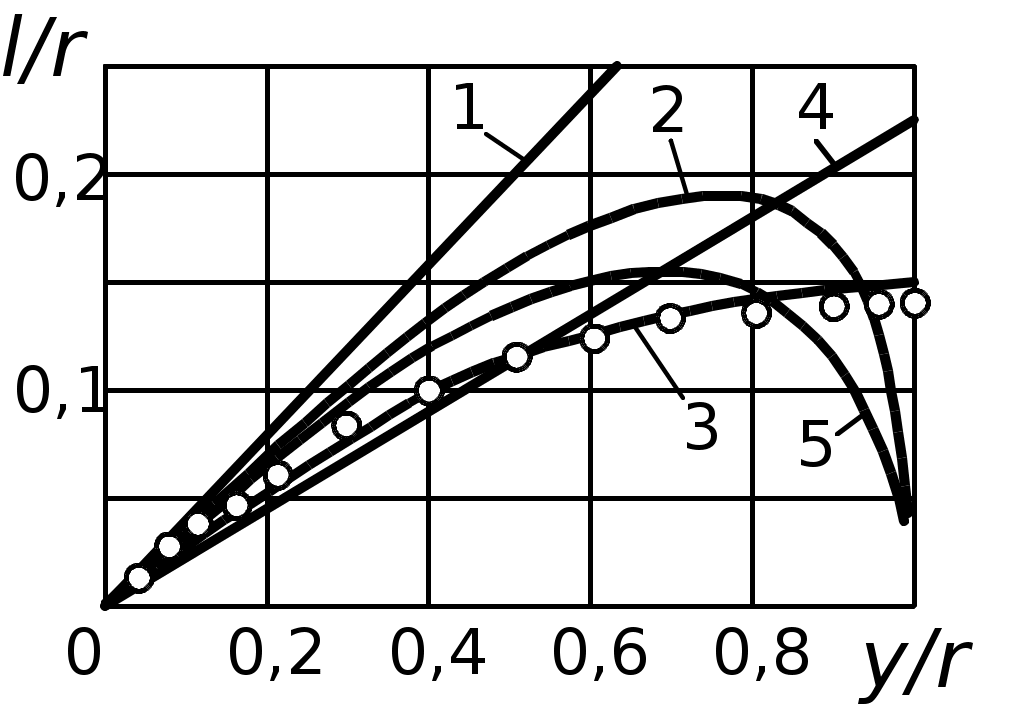
Рисунок 1.5 – Распределение длины пути перемешивания

Существенно отличаются от опытной и кривые, полученные другими авторами: Карманом (кривая 2), Конаковым (кривая 4), Саткевичем (кривая 5). Достаточно близка к эксперименту кривая Альтшуля (кривая 3), описывающая длину пути перемешивания с помощью формулы

. (2.56)

В последнее время Д.Н. Васильевым получена аппроксимирующая зависимость, практически точно совпадающая с данными опыта и имеющая вид

. (2.57)

Использование этого соотношения с учетом линейного распределения касательных напряжений по сечению трубы приводит к закону распределения скоростей, соответствующему гиперболическому тангенсу. Вывод этого соотношения можно найти в [10].

Существуют и другие подходы к этому непростому вопросу. Так, например, А.Д. Альтшуль считает, что разделение потока на две области является грубой схематизацией, носящей искусственный характер. Не оправдана с теоретических позиций гипотеза о ламинарном подслое, как об области, в которой отсутствуют пульсации. Пульсации проникают и в этот слой, но следуют там особым закономерностям. Слабо обосновано и то, что в ядре потока физическая вязкость не играет никакой роли. На базе этих представлений автором разработана полуэмпирическая теория, рассматривающая турбулентный поток в трубе как единое целое, без разделения его на ядро и ламинарный подслой. Достаточно ясное и подробное изложение этой теории можно найти в [1].

Полуэмпирические теории неоднократно подвергались серьезной критике. Главные возражения обычно касались выводов, связанных с особенностями структуры турбулентности. Тем не менее, они широко распространены из-за их простоты и удобства, хотя получаемые результаты достаточно грубы и приближенны. Поэтому нельзя не согласиться с мыслью, высказанной крупнейшим специалистом в области механики жидкости Х. Раузом («Механика жидкости. – М.: Стройиздат, 1967. – 390 с.»): «При сравнении простоты соотношений со сложностью явления вызывает удивление степень их полезности, а не их недостатки».

---

2.3.5 Степенные законы распределения скорости

Логарифмический закон распределения скоростей хорошо подтверждается результатами эксперимента, но вызывает опреде­ленные трудности при численных расчетах. Поэтому в последние годы получают распространение степенные зависимости вида

. (2.58)

Главным достоинством этих формул является их простота, а недостатком – зависимость показателя степени от числа Рейнольдса. Поэтому степенной закон нельзя рассматривать как универсальный. В диапазоне изменения чисел показатель степени 1/n меняется в пределах от 1/6 до 1/10.

Следует отметить, что ни логарифмический, ни степенной законы не удовлетворяют условию равенства нулю производной от скорости на оси симметрии потока.
2.3.6 Потери давления (напора) при турбулентном течении в трубах

Напомним, что рассмотрение закономерностей как ламинарного, так и турбулентного течений в трубах помимо чисто познавательных целей преследовало и цели сугубо практические: получить соотношения, позволяющие определять потери давления (напора) в трубопроводных сетях при выполнении инженерных расчетов. Для ламинарного течения эта задача решается с помощью формулы Хагена-Пуазейля. Из рассмотрения закономерностей турбулентного течения становится ясным, что вследствие его чрезвычайной сложности получение аналогичного соотношения чисто теоретическим путем практически невозможно. Поэтому, основываясь на уже известных положениях, установим хотя бы общую структуру необходимой формулы.

Как было показано, выражение для турбулентных касательных напряжений (напряжений Рейнольдса) имеет вид

. (2.59)

Это с большой долей уверенности позволяет утверждать, что существует связь между средней скоростью и касательным напряжением на стенке трубы вида

, (2.60)

где k – коэффициент пропорциональности.

С другой стороны, из условия равновесия (2.54) движущегося под действием постоянного перепада давления жидкого цилиндра длиной l

---

. (2.61)

После замены радиуса диаметром и подстановки

(2.62)

либо

. (2.63)

В такой форме записи выражение имеет четкий физический смысл. Это так называемое динамическое давление потока, обусловленное средней скоростью, либо кинетическая энергия потока, заключенная в единице объема.

Обозначим величину и назовем ее гидравлическим коэффициентом трения, тогда

(2.64)

либо

. (2.65)

Полученное соотношение носит название формулы Дарси. Более строго это соотношение будет получено методом анализа размерностей.

Отметим попутно, что если в преобразованной формуле Хагена-Пуазейля (2.30) обозначить величину буквой , то она превращается в формулу Дарси. В этом смысле формула Дарси может быть названа универсальной, т.е. пригодной как для ламинарного, так и для турбулентного течений. В последнем случае открытым остается вопрос о нахождении гидравлического коэффициента трения, который, как следует из всего сказанного выше, может быть решен только экспериментальным путем.

В заключение отметим, что хотя поставленная главная проблема и оказалась теоретически неразрешимой, полученные результаты позволяют найти решения ряда частных задач, имеющих важное практическое значение.
2.4 Теплообменные процессы при движении жидкости в трубе. Уравнение теплового баланса Фурье

Процесс теплоотдачи при течении жидкости в трубах является более сложным по сравнению с процессом теплоотдачи при омывании поверхности неограниченным потоком. Жидкость, текущая вдали от поверхности, не испытывает влияния процессов, происходящих у стенки. Поперечное сечение трубы имеет конечные размеры. В результате, начиная с некоторого расстояния от входа, жидкость по всему поперечному сечению трубы испытывает тормозящее действие сил вязкости, происходит изменение температуры жидкости как по сечению, так и по длине канала. Все это сказывается на теплоотдаче.

---

Перенос тепла от жидкости в окружающую среду при трубопроводном транспорте осуществляется одновременно конвекцией, теплопроводностью.

По мере движения жидкости вдоль трубы наблюдается прогрев или охлаждение пристенных слоев, если температура жидкости отлична от температуры трубы. В начале трубы центральное ядро жидкости еще имеет температуру, равную температуре на входе, это ядро в теплообмене не участвует, все изменение температуры сосредоточивается в пристеночном слое. Таким образом, у поверхности трубы в ее начальной части образуется тепловой пограничный слой, толщина которого по мере удаления от входа увеличивается. На некотором расстоянии от входа, равном l (рисунок 1.6), тепловой пограничный слой заполняет все сечение трубы; в дальнейшем вся жидкость участвует в теплообмене, причем интенсивность теплообмена уже не зависит от распределения скорости и температуры на входе. Участок трубы длиной l, называют начальным тепловым участком или участком термической стабилизации. Если при х>l закон задания граничных условий на стенке не изменяется, то такой теплообмен называют стабилизированным. В отличие от эпюр скорости эпюры температур при х>l даже в случае постоянных физических свойств жидкости не остаются неизмененными.



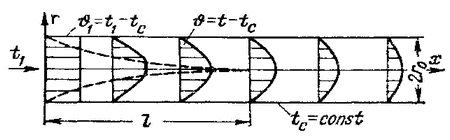
Рисунок 1.6 – Распределение эпюр температур вдоль трубы

В связи с переменностью физических параметров могут иметь место два режима неизотермического движения нефти: вязкостный и вязкостно-гравитационный. Законы теплоотдачи для этих двух режимов различны. В вязкостно-гравитационном течении силы вязкости и подъемные силы соизмеримы. Вязкостный режим имеет место при преобладании сил вязкости над подъемными силами, т. е. он соответствует течению вязких жидкостей при отсутствии влияния естественной конвекции. По сравнению с вязкостно-гравитационным вязкостный режим тем более вероятен, чем меньше диаметр трубы, чем больше вязкость жидкости и чем меньше температурный напор. При вязкостном режиме распределение скорости по сечению трубы отклоняется от параболического, так как вследствие изменения температуры по сечению изменяется и вязкость. При этом распределение скоростей зависит от того, имело ли место нагревание или охлаждение жидкостей.

---

Смотрите также файлы

• Темы занятий.docx

• Химический факультет отчет по учебной практике.docx

• Разговор о важном 23 января 2023 г.docx

• Тема вкр Моделирование специальной физической подготовки в тренировочном процессе биатлонистов оглавление.docx

• Бортовые магнитофоны.pptx