и изгибные напряжения. Расчет закрытой цилиндрической прямозубой передачи в курсовой работе приведен только по контактным напряжениям, так как большая статистика расчетов этих передач при средних режимах нагружения и длительном режиме эксплуатации оказывает, что при обеспечении контактной прочности изгибная прочность выполняется. В качестве исходных данных для расчета зубчатой передачи примем материалы и механические характеристики шестерни и колеса, приведенные в таблице 3.1.
Таблица 3.1 – Материалы колес и их механические характеристики

Характеристики	Шестерня	Колесо
Марка стали	Сталь 40Х ГОСТ 4543	Сталь 45 ГОСТ1050
Метод получения заготовки	Поковка	Поковка
Термическая обработка	Улучшение	Улучшение
Интервал твердости, НВ	269…302	235…262
Средняя твердость, НВср	285,5	248,5
Предел текучести, Т, МПа	750	540
Предел прочности, В, МПа	900	780
Допускаемое контактное напряжение: шестерни – [Н1], колеса – [ Н2], МПа	583	515
Максимально допускаемое контактное напряжение при перегрузках [ Нмах], МПа	2100	1512
Допускаемое напряжение изгиба шестерни – [F1], колеса – [F2], МПа	294	255
Максимальное напряжение изгиба при перегрузках [Fмах], МПа	771	671

4 Расчет прямозубой цилиндрической зубчатой передачи

---

Главный геометрический параметр цилиндрической зубчатой передачи – межосевое расстояние (рисунок 4.1). Предварительное его значение рассчитывается из условия контактной выносливости рабочих поверхностей зубьев по формуле
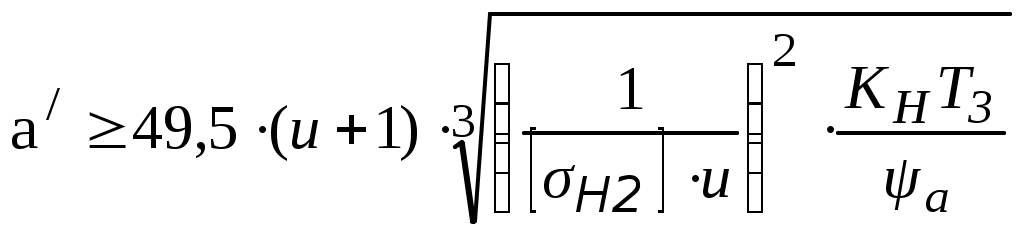, (4.1)

где Т₃ – вращающий момент на валу колеса (3-й вал привода), Нмм;

K_H– коэффициент нагрузки колес при расчете по контактным напряжениям (К_н = 1,2);

_а– коэффициент ширины колеса. Для одноступенчатого цилиндрического редуктора при симметричном расположении колес относительно опор _а = 0,4 или 0,5;

u – передаточное число зубчатой передачи, u = u_ЗП;

[_Н2] – допускаемое контактное напряжение для материала колеса, так как колесо имеет более низкую прочность по сравнению с шестерней.

Рассчитаем предварительное значение межосевого расстояния
^.





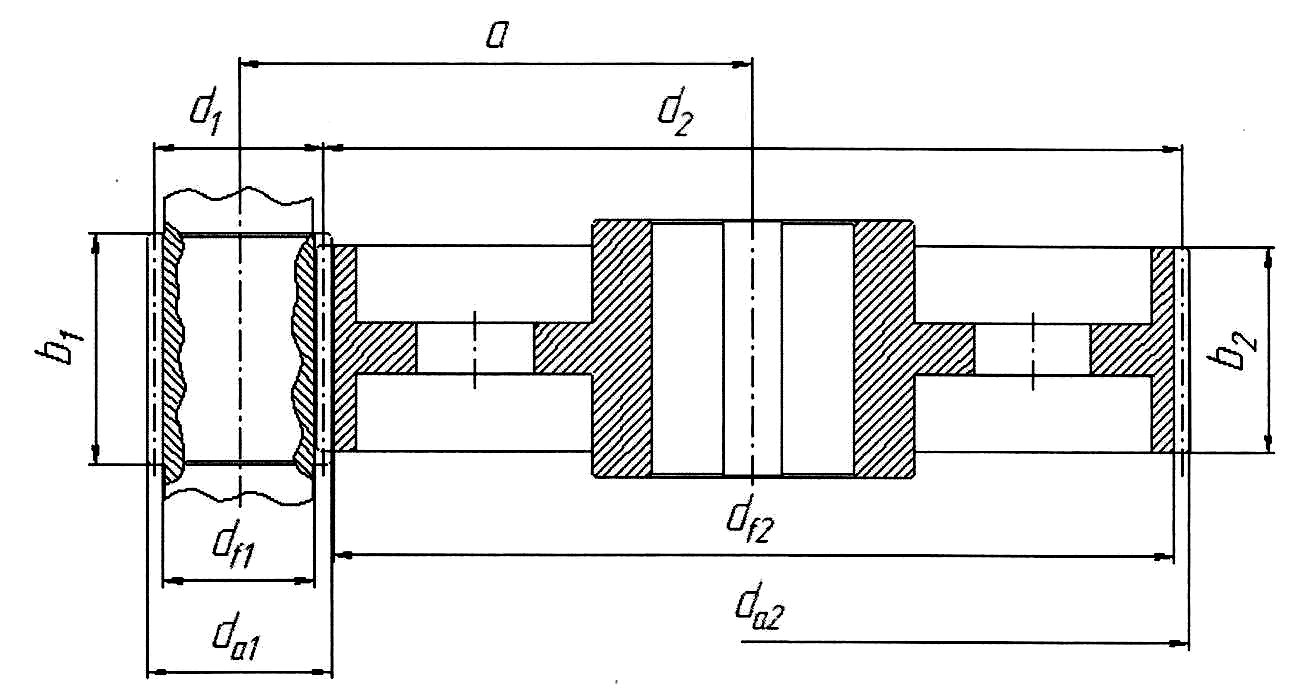
Рисунок 4.1 – Геометрические параметры цилиндрической

зубчатой передачи

Значение округляем до ближайшего значения по единому ряду главных параметров механических передач.

Принимаем = 180.

Определяем предварительные значения ширины зубчатого колеса и шестерни:
, (4.2)
(4.3)
Значения и не совпадают со стандартными значениями из ряда главных параметров, принимаем b₁ = 80 мм; b₂ = 71 мм.

Модуль зубчатых колес выбираем в следующем интервале:
m^/= (0,01… 0,02)

---

 а = (0,01…0,02) 180 = 1,8… 3,6 мм . (4.4)
Выбираем модуль m = 2,5 мм.

Определим число зубьев колес. Предварительное суммарное число зубьев колес вычисляем из соотношения:
(4.5)

Предварительное значение числа зубьев шестерни находят из соотношения:
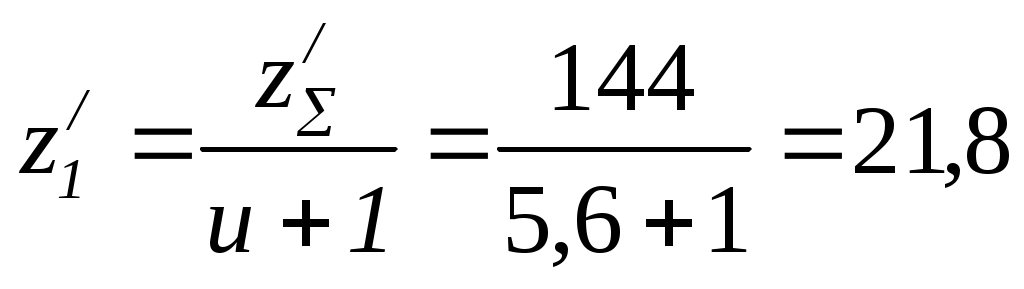. (4.6)

Округляем полученное значение z^/₁  до ближайшего целого значения z₁ = 22.

После этого вычисляем число зубьев колеса z₂:
. (4.7)
Таким образом, z₂ = 122 и z₁ = 22.

Уточним фактическое передаточное число передачи:

u_ф = z₂ / z₁ = 122 / 22 = 5,5. (4.8)

Отклонение фактического передаточного числа составляет:

. (4.9)
Проверка прочности зубьев колес по контактным напряжениям проводится по следующему условию прочности:

, (4.10)
где К_H – коэффициент нагрузки зубьев колеса при расчете по контактным напряжениям определяется по формуле:
К_H = К_Hα · К_Hβ · К_HV, (4.11)
где К_Hα– коэффициент распределения нагрузки между зубьями (для прямозубых колес К_Hα= 1);

К_Hβ– коэффициент концентрации нагрузки;

К_HV – коэффициент динамичности.

Значение коэффициента К_Hβ при расчете определяется в зависимости от коэффициента ширины колеса относительно диаметра ψ_bd, который определяют по формуле:
ψ_bd = 0,5 · ψ_a · ( и+ 1), (4.12)
где ψ_a – коэффициент ширины колеса относительно межосевого расстояния.

При ψ_bd = 0,5 · 0,4 · (5,6+1) = 1,32, К_Нβ = 1,13.
Коэффициент динамичности К_HV зависит от окружной скорости вращения колес V₂, рассчитываемой по зависимости:
. (4.13)

По полученным данным V₂ = 2,1 м/с. Этой скорости соответствует 8-я степень точности. Определим значение коэффициента

---

К_HV с помощью линейной интерполяции. Получим К_HV =1,084.

Тогда коэффициент нагрузки при расчете по контактным напряжениям:
К_H = 1· 1,13 · 1,084 = 1,22.

Действительное контактное напряжение равно:

Фактическая недогрузка для рассматриваемого задания составит:
, (4.14)
что меньше 15 %, а значит, допустимо.

Проверяем зубчатую передачу на кратковременные перегрузки:

— по контактным напряжениям
σ_{Нmax 2} = σ_Н2 · = 485 · = 668,5 МПа; (4.15)
[σ_{Н max2}] = 2,8 · σ_Т = 2,8 · 540 = 1512 МПа; (4.16)
σ_{Нmax 2} < [σ_{Н max2}].
Проверочный расчет на усталостную прочность по напряжениям изгиба зубьев колеса проводим по формуле:
σ_F2 = Υ_F2 · F_t2 · K_F· K_FD/(b₂ m) ≤ [σ_F2], (4.17)

где Υ_F2 – коэффициент формы зуба колеса (Υ_F2 = 3,6);

F_t2 – окружное усилие в зацеплении зубчатых колёс, Н;

K_F– коэффициент нагрузки при расчете по напряжениям изгиба;

K_FD– коэффициент долговечности (принимаем K_FD =1).

Коэффициент нагрузки при расчете на изгиб определяется по формуле:
K_F = K_Fα· K_Fβ· K_FV, (4.18)
где K_Fα – коэффициент неравномерности распределения нагрузкимежду парами зубьев (для прямозубых колес K_Fα = 1);

К_Fβ – коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий (К_Fβ = 1,15);

К_FV– коэффициент, учитывающий внутреннюю динамическую нагрузку при расчете зубьев на прочность при изгибе (К_FV = 1,209).

Тогда, коэффициент нагрузки при расчете на изгиб:
K_F = 1 · 1,15 · 1,209 = 1,39.
Окружная сила в зубчатом зацеплении равна:
F_t2 = F _t1 = Т₃

---

· (u+1)/(a · u) = 487650 · (5,6+1) /(180 · 5,6) = 3193 Н. (4.19)
Тогда получим σ_F2 = 3,6 · 3193 · 1,39 · 1 / (71 · 2,5) = 90 МПа, что меньше [σ_F2] = 255 МПа.

Таким образом, условие прочности на изгиб выполняется.

Проверяем зубчатую передачу на кратковременные перегрузки по напряжениям изгиба
σ_{Fmax 2} = σ_F2· К_п= 90 · 1,9 = 171 МПа < [σ_{F max2}] = 671 МПа. (4.20)

Определим другие геометрические размеры колес, мм.

Делительные диаметры равны:

, (4.21)

. (4.22)

Диаметры вершин зубьев равны:

, (4.23)

. (4.24)
Диаметры впадин зубьев равны:
, (4.25)

. (4.26)
Проверим межосевое расстояние зубчатых колес:
а = (d₁ +d₂) / 2 = (55 + 305) / 2 = 180 мм. (4.27)
В прямозубой цилиндрической передаче при работе возникают силы в зацеплении зубьев.

---

Смотрите также файлы

• мусор. Net.docx

• Особенности экономического развития россии в пореформенный период.docx

• Построение моделей идентификации.doc

• Реферат Таырыбы Титриметриялы анализ. Орындаан Кшербаева А.. химия31 студенті Мамандыы.docx

• Сталинградская битва. Начало коренного перелома. 17 Июля1941 2 февраля 1942 Период коренного перелома (Коренной перелом) радикальное изменение сил в ходе Великой Отечественной войны,.docx